Значения температурного коэффициента для некоторых металлов
| Металл | α | ||
| Серебро Медь Железо Вольфрам Платина | 0,0035 0,0040 0,0066 0,0045 0,0032 | Ртуть Никелин Константан Нихром Манганин | 0,0090 0,0003 0,000005 0,00016 0,00005 |
Из формулы температурного коэффициента сопротивления определим rt:
Пример 6. Определить сопротивление железной проволоки, нагретой до 200°C, если сопротивление ее при 0°C было 100 Ом.
Пример 7. Термометр сопротивления, изготовленный из платиновой проволоки, в помещении с температурой 15°C имел сопротивление 20 Ом. Термометр поместили в печь и через некоторое время было измерено его сопротивление. Оно оказалось равным 29,6 Ом. Определить температуру в печи.
Проводник
Проводник
— вещество, имеющее свободные носители заряда (заряженные частицы), способные, в отличие от диэлектриков свободно перемещаться внутри этого вещества; их движением обусловлена возможность проводить электрический ток.
Кроме того, под термином «проводник» в электротехнике принято понимать провода или шины, предназначенные для соединений в электрических цепях.
Разновидности проводников
. В зависимости от природы и механизма электропроводности их подразделяют на проводники первого и второго рода.
К первым можно отнести вещества с электронной проводимостью, обусловленной движением электронов в цепи от отрицательного полюса положительному. Ко вторым — вещества с ионной проводимостью.
В качестве примера проводников первого рода можно привести все металлы (их сплавы) а также, каменный уголь, графит, сажа и пр. Проводники второго рода — это электролиты (р-ры кислот, щелочи и соли, находящиеся растворенном, расплавленном или кристаллическом состоянии) и т. д.
Основные параметры проводниковых материалов:
Удельная проводимость проводника (σ)
— величина, обратная удельному сопротивлению (р ). Является наиболее важным параметром, характеризующим свойства проводникового материала. Наиболее широко в электротехнике используются чистые металлы и сплавы металлов с низким удельным сопротивлением (р =0,015-0,108 ом*мм2/м).
Температурный коэффициент удельного сопротивления (αρ)
— показатель зависимости сопротивления проводника от его температуры. Так, при увеличении температуры увеличивается и удельное сопротивление большинства проводников.
Теплопроводность
— его способность передавать теплоту. Для количественной оценки данной характеристики существует коэффициент теплопроводности (γт ).
Ввиду того, что передача тепла в веществах осуществляется посредством электронов, коэффициент теплопроводности металлов, имеющих их наибольшее количество будет значительно превышать γт
диэлектриков. Так, с увеличением температуры вещества связано снижение его удельной проводимости и отношениеγт к его удельной проводимости будет увеличиваться.
Контактная разность потенциалов
— разность потенциалов между двумя находящимися в контакте проводниками с одинаковой температурой. Их соединение сопровождается обменом электронами — заряд проводника с большей работой выхода отрицательно, с меньшей — положительно.
Их зарядка будет происходить до уравновешивания потоков движущихся электронов в обоих направлениях и не произойдет уравнивание электрохимического потенциала в системе.
Работа выхода электронов из металла
— энергия, расходуемая на удаление электрона из поверхностного электронного слоя проводника.
Предел прочности при растяжении σρ и относительное удлинение перед разрывом Δl/l
— показатели, характеризующие механические свойства материала.
Электрическое сопротивление
Электрическое сопротивление, одно из составляющих закона Ома, выражается в омах (Ом). Следует заметить, что электрическое сопротивление и удельное сопротивление — это не одно и то же. Удельное сопротивление является свойством материала, в то время как электрическое сопротивление — это свойство объекта.
Электрическое сопротивление резистора определяется сочетанием формы и удельным сопротивлением материала, из которого он сделан.
Стенд для пайки со светодиодной подсветкой
Материал: АБС + металл + акриловые линзы. Светодиодная подсветка…
Подробнее
Например, проволочный резистор, изготовленный из длинной и тонкой проволоки имеет большее сопротивление, нежели резистор, сделанный из короткой и толстой проволоки того же металла.
В тоже время проволочный резистор, изготовленный из материала с высоким удельным сопротивлением, обладает большим электрическим сопротивлением, чем резистор, сделанный из материала с низким удельным сопротивлением. И все это не смотря на то, что оба резистора сделаны из проволоки одинаковой длины и диаметра.
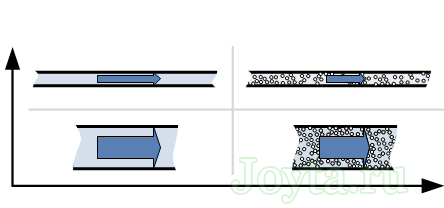
В качестве наглядности можно провести аналогию с гидравлической системой, где вода прокачивается через трубы.
- Чем длиннее и тоньше труба, тем больше будет оказано сопротивление воде.
- Труба, заполненная песком, будет больше оказывать сопротивление воде, нежели труба без песка
Зависимость сопротивления проводника от температуры
Удельное сопротивление, а следовательно, и сопротивление металлов, зависит от температуры, увеличиваясь с ее ростом. Температурная зависимость сопротивления проводника объясняется тем, что
- возрастает интенсивность рассеивания (число столкновений) носителей зарядов при повышении температуры;
- изменяется их концентрация при нагревании проводника.
Опыт показывает, что при не слишком высоких и не слишком низких температурах зависимости удельного сопротивления и сопротивления проводника от температуры выражаются формулами:
где ρ, ρt — удельные сопротивления вещества проводника соответственно при 0 °С и t °C; R, Rt — сопротивления проводника при 0 °С и t °С, α — температурный коэффициент сопротивления: измеряемый в СИ в Кельвинах в минус первой степени (К-1). Для металлических проводников эти формулы применимы начиная с температуры 140 К и выше.
Температурный коэффициент сопротивления вещества характеризует зависимость изменения сопротивления при нагревании от рода вещества. Он численно равен относительному изменению сопротивления (удельного сопротивления) проводника при нагревании на 1 К.
где \(~\mathcal h \alpha \mathcal i\) — среднее значение температурного коэффициента сопротивления в интервале ΔΤ.
Для всех металлических проводников α > 0 и слабо изменяется с изменением температуры. У чистых металлов α = 1/273 К-1. У металлов концентрация свободных носителей зарядов (электронов) n = const и увеличение ρ происходит благодаря росту интенсивности рассеивания свободных электронов на ионах кристаллической решетки.
Для растворов электролитов α < 0, например, для 10%-ного раствора поваренной соли α = -0,02 К-1. Сопротивление электролитов с ростом температуры уменьшается, так как увеличение числа свободных ионов из-за диссоциации молекул превышает рост рассеивания ионов при столкновениях с молекулами растворителя.
Формулы зависимости ρ и R от температуры для электролитов аналогичны приведенным выше формулам для металлических проводников. Необходимо отметить, что эта линейная зависимость сохраняется лишь в небольшом диапазоне изменения температур, в котором α = const. При больших же интервалах изменения температур зависимость сопротивления электролитов от температуры становится нелинейной.
Графически зависимости сопротивления металлических проводников и электролитов от температуры изображены на рисунках 1, а, б.
При очень низких температурах, близких к абсолютному нулю (-273 °С), сопротивление многих металлов скачком падает до нуля. Это явление получило название сверхпроводимости. Металл переходит в сверхпроводящее состояние.
Зависимость сопротивления металлов от температуры используют в термометрах сопротивления. Обычно в качестве термометрического тела такого термометра берут платиновую проволоку, зависимость сопротивления которой от температуры достаточно изучена.
Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить. Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.
Какие существуют виды
Их немного, одно из которых мы уже разобрали:
- омическое;
- активное;
- индуктивное;
- ёмкостное.
Формулы расчёта электрического сопротивления для переменного тока
К сожалению, наш друг-физик решил не идти нам навстречу и вывел несколько формул по нахождению всех трёх величин. Электрическое сопротивление обозначается буквой R.
Но перед тем как пойти дальше, совет: всегда придумывайте какие-нибудь ассоциации, чтобы запомнилось на всю жизнь, например:
- R (сопротивление). Можете запомнить что R, как рюмка. Нужно сопротивляться, чтобы не выпить ещё одну рюмку.
- I (сила тока). Латинская «I», как проводок, по которому идёт ток.
- U (напряжение). Эта буква, как дуга. И напряжение разносится с одного конца на другой по дуге.
Ну и, конечно, формула закона Ома для участка цепи.
- R=U/I т.е., чтобы найти сопротивление(рюмку) надо напряжение (дугу) разделить на ток (проводок).
- U=IR, хотите найти напряжение (дугу), умножьте проводок на рюмку.
- I=U/R чтобы найти чему равен проводок, нужно напряжение разделить на сопротивление.
Ну а теперь главное, для чего мы все здесь собрались: «Зачем нужен этот закон? Что он даёт?»
Также не забывате, если вдруг вас спросят от чего зависит сопротивление — отвечайте: » От напряжения и мощности».
Активного сопротивления
Ну что сказать? Придется запастись терпением и потратить время на все эти законы и определения.
Но к счастью, активное сопротивление, так и осталось большой буквой R. Просто немного поменялась формула и ее предназначение.
Подключим к нашей цепи проводник. Проводником может выступать лампа.
Понятно, что по нему тоже будет проходить ток. Это как танец «волна». Все 5 человек берутся за руки и начинают по очереди создавать колебания. Сопротивление уже известно на всех. Так же и здесь.
Если посмотреть, то можно найти сходство танца «волны» с этой буквой. Так и запомните.
Формула, как рассчитать силу тока:
I=U/Z
Индуктивного сопротивления
Боюсь, что когда вы увидите данную формулу, то она вам точно не понравится. Но нет слова «не хочу», есть слово «надо».
Начнем с обозначения:
- XL (индуктивное сопротивление). Прямо как размер в одежде. Но почему именно так? L — это цепь переменного тока;
- f — частота, в Гц;
- сопротивление с частотой взаимосвязаны, так, если возрастает одно — увеличивается и другое;
- единица СИ индуктивного сопротивления: = Ом;
- запомните, что индуктивное сопротивление отличается от омического тем, что у первого нет потери мощности;
- XL=2π×f×L;
- формула расчета мощности по напряжению: P = U×I;
- мощность электрического тока вычисляется в Ватах.
Емкостного
Ёмкостное сопротивление — это проводник, который подключен к цепи. Он не имеет сопротивление, но есть ёмкость. Обозначается это ёмкостное сопротивление буквами Xc.
- Xc = 1/ωC;
- ω — циклическая частота;
- С — ёмкость.
Полного
Как говорилось выше — полное сопротиление что-то на подобии танца «волны». Нужно узнать R (сопротивление) всех.
Чтобы определить полное сопротивление цепи:
R = R1 +R2 (проводников может быть несколько).
Теперь, если у вас спросят как определить общее сопротивление цепи, вы знаете что делать.
Формула
Общее электросопротивление проводника можно найти по представленной выше формуле. Что касается нахождения показаний для активной, реактивной, отрицательной и удельной разновидности, есть свои специальные формулы. Все они представлены в соответствующей схеме далее с обозначениями.

Формулы, используемые для расчета значения проводника
Электросопротивление в электродинамике является электротехнической величиной, характеризующей способность металла препятствовать электрическому току. При расчетах используется буква R, вне зависимости от того, какое сопротивление изучается и подсчитывается. Формул для нахождения величины множество. В основном используется R=U/I.
Физика явления[ | ]
Высокая электропроводность металлов связана с тем, что в них имеется большое количество носителей тока — электронов проводимости
, образующихся из валентных электронов атомов металла, которые не принадлежат определённому атому. Электрический ток в металле возникает под действием внешнего электрического поля, которое вызывает упорядоченное движение электронов. Движущиеся под действием поля электроны рассеиваются на неоднородностях ионной решётки (на примесях, дефектах решётки, а также нарушениях периодической структуры, связанной с тепловыми колебаниями ионов). При этом электроны теряют импульс, а энергия их движения преобразуются во внутреннюю энергию кристаллической решётки, что и приводит к нагреванию проводника при прохождении по нему электрического тока.
В других средах (полупроводниках, диэлектриках, электролитах, неполярных жидкостях, газах и т. д.) в зависимости от природы носителей заряда физическая причина сопротивления может быть иной. Линейная зависимость, выраженная законом Ома, соблюдается не во всех случаях.
Сопротивление проводника при прочих равных условиях зависит от его геометрии и от удельного электрического сопротивления
материала, из которого он состоит.
Сопротивление однородного проводника постоянного сечения зависит от свойств вещества проводника, его длины, сечения и вычисляется по формуле:
R = ρ ⋅ l S , {\displaystyle R={\frac {\rho \cdot l}{S}},}
где ρ — удельное сопротивление
вещества проводника, Ом·м,l — длина проводника, м, аS — площадь сечения, м².
Сопротивление однородного проводника также зависит от температуры.
Удельное сопротивление — скалярная физическая величина, численно равная сопротивлению однородного цилиндрического проводника единичной длины и единичной площади сечения.
Сопротивление металлов снижается при понижении температуры; при температурах порядка нескольких кельвинов сопротивление большинства металлов и сплавов стремится или становится равным нулю (эффект сверхпроводимости). Напротив, сопротивление полупроводников и изоляторов при снижении температуры (в некотором диапазоне) растёт. Сопротивление также меняется по мере увеличения тока/напряжения, протекающего через проводник/полупроводник.
Характеристики
Исследовав электрический ток и его ключевые характеристики, возможно понять принцип его функционирования. Главными величинами электрической энергии являются напряжение, сила и сопротивление.
Сила и плотность тока
Чтобы описать характеристики электричества, зачастую применяют термин «сила тока». Он определяет интенсивность перемещения зарядов, которые проходят сквозь поперечное сечение проводника.
Плотность тока является векторной величиной. Вектор направляется в сторону движения положительно заряженных зарядов. Его модуль равняется соотношению силы электротока на определенном перпендикулярном по направлению перемещения зарядов сечении проводника к его площади. Измерение происходит в амперах на метр.
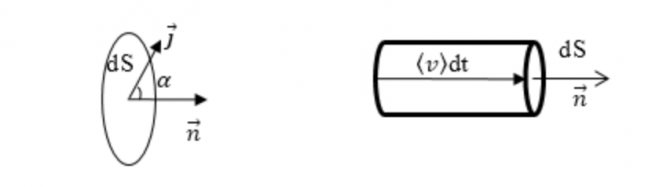
Плотность тока
Мощность
Электрические силы осуществляют работу против активного и реактивного сопротивления. На пассивных работах будет преобразовываться в теплоэнергию. Производительностью называется работа, которая выполнена за 1 врем. ед. Относительно электричества применяется понятие «мощность теплопотерь». Мощность теплопотерь проводника равняется силе тока, которая умножена на напряжение. Измеряется мощность в ваттах.
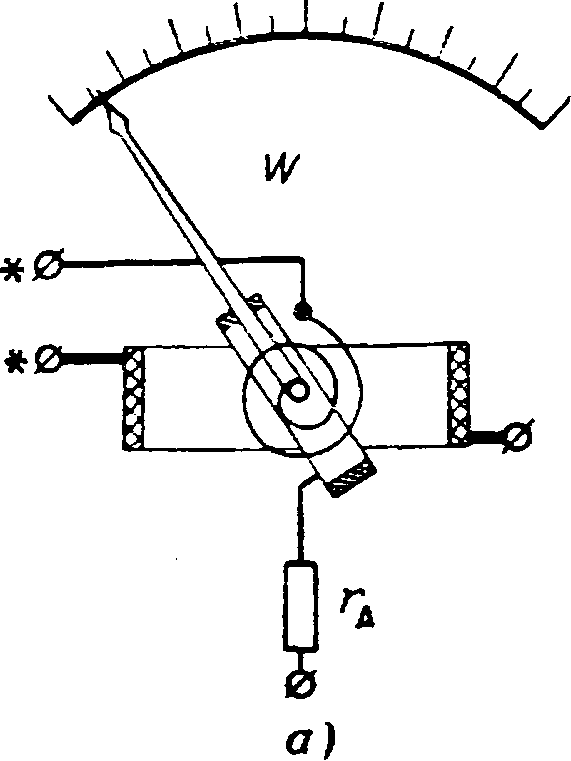
Мощность
Частота
Ток характеризует частота. Такой параметр покажет, как за врем. ед. меняется число колебаний. Частота измеряется в герцах. Обычная промышленная частота составит 50 Гц.
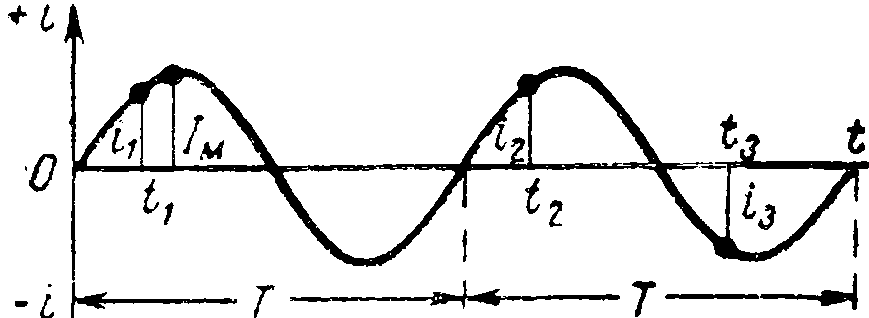
Частота
Ток смещения
Такой термин был введен для комфорта, хотя в привычном понимании его не назовешь током, поскольку нет переноса заряда. Интенсивность электромагнитного поля находится в зависимости от токопроводимости и смещения.
Токи смещения возможно увидеть в конденсаторе. Невзирая на то, что во время зарядки и разрядки меж обкладок конденсатора не перемещается заряд, ток смещения будет протекать сквозь конденсатор и замыкать электроцепь.
Советуем изучить — Преимущества системы дистанционного радиоуправления кранами telecrane
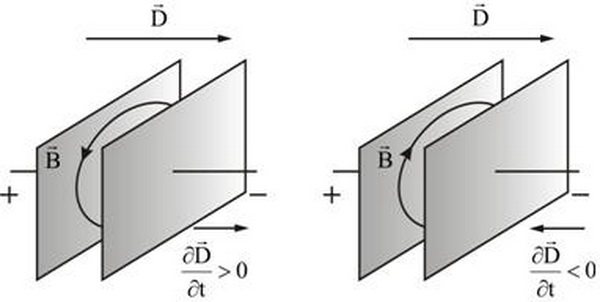
Ток смещения
Связь с удельной проводимостью[ | ]
В изотропных материалах связь между удельным сопротивлением ρ {\displaystyle \rho } и удельной проводимостью σ {\displaystyle \sigma } выражается равенством
ρ = 1 σ . {\displaystyle \rho ={\frac {1}{\sigma }}.}
В случае анизотропных материалов связь между компонентами тензора удельного сопротивления ρ i j {\displaystyle \rho _{ij}} и тензора удельной проводимости σ i j {\displaystyle \sigma _{ij}} имеет более сложный характер. Действительно, закон Ома в дифференциальной форме для анизотропных материалов имеет вид:
J i ( r → ) = ∑ j = 1 3 σ i j ( r → ) E j ( r → ) . {\displaystyle J_{i}({\vec {r}})=\sum _{j=1}^{3}\sigma _{ij}({\vec {r}})E_{j}({\vec {r}}).}
Из этого равенства и приведённого ранее соотношения для E i ( r → ) {\displaystyle E_{i}({\vec {r}})} следует, что тензор удельного сопротивления является обратным тензору удельной проводимости. С учётом этого для компонент тензора удельного сопротивления выполняется:
ρ 11 = 1 det ( σ ) , {\displaystyle \rho _{11}={\frac {1}{\det(\sigma )}},} ρ 12 = 1 det ( σ ) , {\displaystyle \rho _{12}={\frac {1}{\det(\sigma )}},}
где det ( σ ) {\displaystyle \det(\sigma )} — определитель матрицы, составленной из компонент тензора σ i j {\displaystyle \sigma _{ij}} . Остальные компоненты тензора удельного сопротивления получаются из приведённых уравнений в результате циклической перестановки индексов 1
,2 и3 .
Удельное электрическое сопротивление
Сопротивление в омах проводника длиной 1 м, сечением 1 мм² называется удельным сопротивлением
и обозначается греческой буквойρ (ро).
В таблице 1 даны удельные сопротивления некоторых проводников.
Таблица 1
Удельные сопротивления различных проводников
Из таблицы видно, что железная проволока длиной 1 м и сечением 1 мм² обладает сопротивлением 0,13 Ом. Чтобы получить 1 Ом сопротивления нужно взять 7,7 м такой проволоки. Наименьшим удельным сопротивлением обладает серебро. 1 Ом сопротивления можно получить, если взять 62,5 м серебряной проволоки сечением 1 мм². Серебро – лучший проводник, но стоимость серебра исключает возможность его массового применения. После серебра в таблице идет медь: 1 м медной проволоки сечением 1 мм² обладает сопротивлением 0,0175 Ом. Чтобы получить сопротивление в 1 Ом, нужно взять 57 м такой проволоки.
Химически чистая, полученная путем рафинирования, медь нашла себе повсеместное применение в электротехнике для изготовления проводов, кабелей, обмоток электрических машин и аппаратов. Широко применяют также в качестве проводников алюминий и железо.
Сопротивление проводника можно определить по формуле:
где r
– сопротивление проводника в омах;ρ – удельное сопротивление проводника;l – длина проводника в м;S – сечение проводника в мм².
Пример 1.
Определить сопротивление 200 м железной проволоки сечением 5 мм².
Пример 2.
Вычислить сопротивление 2 км алюминиевой проволоки сечением 2,5 мм².
Из формулы сопротивления легко можно определить длину, удельное сопротивление и сечение проводника.
Пример 3.
Для радиоприемника необходимо намотать сопротивление в 30 Ом из никелиновой проволоки сечением 0,21 мм². Определить необходимую длину проволоки.
Пример 4.
Определить сечение 20 м нихромовой проволоки, если сопротивление ее равно 25 Ом.
Пример 5.
Проволока сечением 0,5 мм² и длиной 40 м имеет сопротивление 16 Ом. Определить материал проволоки.
Материал проводника характеризует его удельное сопротивление.
По таблице удельных сопротивлений находим, что таким сопротивлением обладает свинец.
Выше было указано, что сопротивление проводников зависит от температуры. Проделаем следующий опыт. Намотаем в виде спирали несколько метров тонкой металлической проволоки и включим эту спираль в цепь аккумулятора. Для измерения тока в цепь включаем амперметр. При нагревании спирали в пламени горелки можно заметить, что показания амперметра будут уменьшаться. Это показывает, что с нагревом сопротивление металлической проволоки увеличивается.
У некоторых металлов при нагревании на 100° сопротивление увеличивается на 40 – 50 %. Имеются сплавы, которые незначительно меняют свое сопротивление с нагревом. Некоторые специальные сплавы практически не меняют сопротивления при изменении температуры. Сопротивление металлических проводников при повышении температуры увеличивается, сопротивление электролитов (жидких проводников), угля и некоторых твердых веществ, наоборот, уменьшается.
Способность металлов менять свое сопротивление с изменением температуры используется для устройства термометров сопротивления. Такой термометр представляет собой платиновую проволоку, намотанную на слюдяной каркас. Помещая термометр, например, в печь и измеряя сопротивление платиновой проволоки до и после нагрева, можно определить температуру в печи.
Изменение сопротивления проводника при его нагревании, приходящееся на 1 Ом первоначального сопротивления и на 1° температуры, называется температурным коэффициентом сопротивления
и обозначается буквой α.
Если при температуре t
0 сопротивление проводника равноr 0 , а при температуреt равноr t , то температурный коэффициент сопротивления
Примечание.
Расчет по этой формуле можно производить лишь в определенном интервале температур (примерно до 200°C).
Приводим значения температурного коэффициента сопротивления α для некоторых металлов (таблица 2).
Таблица 2
Значения температурного коэффициента для некоторых металлов
Из формулы температурного коэффициента сопротивления определим r t
r t
=r 0 .
Пример 6.
Определить сопротивление железной проволоки, нагретой до 200°C, если сопротивление ее при 0°C было 100 Ом.
r t
=r 0 = 100 (1 + 0,0066 × 200) = 232 Ом.
Пример 7.
Термометр сопротивления, изготовленный из платиновой проволоки, в помещении с температурой 15°C имел сопротивление 20 Ом. Термометр поместили в печь и через некоторое время было измерено его сопротивление. Оно оказалось равным 29,6 Ом. Определить температуру в печи.
Удельное сопротивление металлов, электролитов и веществ (Таблица)
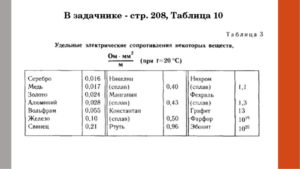
В справочной таблице даны значения удельного сопротивления р некоторых металлов и изоляторов при температуре 18—20° С, выраженные в ом·см.
Величина р для металлов в сильной степени зависит от примесей, в таблице даны значения р для химически чистых металлов, для изоляторов даны приближенно.
Металлы и изоляторы расположены в таблице в порядке возрастающих значений р.
Таблица удельное сопротивление металлов
| Чистые металлы | 104 ρ (ом·см) | Чистые металлы | 104 ρ (ом·см) |
| Серебро | 0,016 | Хром | 0,131 |
| Медь | 0,017 | Тантал | 0,146 |
| Золото | 0,023 | Бронза 1) | 0,18 |
| Алюминий | 0,029 | Торий | 0,18 |
| Дюралюминий | 0,0335 | Свинец | 0,208 |
| Магний | 0,044 | Платинит 2) | 0,45 |
| Кальций | 0,046 | Сурьма | 0,405 |
| Натрий | 0,047 | Аргентан | 0,42 |
| Марганец | 0,05 | Никелин | 0,33 |
| Иридий | 0,063 | Манганин | 0,43 |
| Вольфрам | 0,053 | Константан | 0,49 |
| Молибден | 0,054 | Сплав Вуда 3) | 0,52 (0°) |
| Родий | 0,047 | Осмий | 0,602 |
| Цинк | 0,061 | Сплав Розе 4) | 0,64 (0°) |
| Калий | 0,066 | Хромель | 0,70-1,10 |
| Никель | 0,070 | ||
| Кадмий | 0,076 | Инвар | 0,81 |
| Латунь | 0,08 | Ртуть | 0,958 |
| Кобальт | 0,097 | Нихром 5) | 1,10 |
| Железо | 0,10 | Висмут | 1,19 |
| Палладий | 0,107 | Фехраль 6) | 1,20 |
| Платина | 0,110 | Графит | 8,0 |
| Олово | 0,113 |
Таблица удельное сопротивление изоляторов
| Изоляторы | ρ (ом·см) | Изоляторы | ρ (ом·см) |
| Асбест | 108 | Слюда | 1015 |
| Шифер | 108 | Миканит | 1015 |
| Дерево сухое | 1010 | Фарфор | 2·1015 |
| Мрамор | 1010 | Сургуч | 5·1015 |
| Целлулоид | 2·1010 | Шеллак | 1016 |
| Бакелит | 1011 | Канифоль | 1016 |
| Гетинакс | 5·1011 | Кварц _|_ оси | 3·1016 |
| Алмаз | 1012 | Сера | 1017 |
| Стекло натр | 1012 | Полистирол | 1017 |
| Стекло пирекс | 2·1014 | Эбонит | 1018 |
| Кварц || оси | 1014 | Парафин | 3·1018 |
| Кварц плавленый | 2·1014 | Янтарь | 1019 |
Удельное сопротивление чистых металлов при низких температурах
В таблице даны значения удельного сопротивления (в ом·см) некоторых чистых металлов при низких температурах (0°С).
| Чистые металлы | t (°С) | Удельное сопротивление, 104 ρ (ом·см) |
| Висмут | -200 | 0,348 |
| Золото | -262,8 | 0,00018 |
| Железо | -252,7 | 0,00011 |
| Медь | -258,6 | 0,00014 1 |
| Платина | -265 | 0,0010 |
| Ртуть | -183,5 | 0,0697 |
| Свинец | -252,9 | 0,0059 |
| Серебро | -258,6 | 0,00009 |
Отношение сопротивлении Rt/Rq чистых металлов при температуре Т °К и 273° К
В справочной таблице дано отношение Rt/Rq сопротивлений чистых металлов при температуре Т °К и 273° К.
| Чистые металлы | Т (°К) | RT/R0 |
| Алюминий | 77,7 | 1,008 |
| 20,4 | 0,0075 | |
| Висмут | 77,8 | 0,3255 |
| 20,4 | 0,0810 | |
| Вольфрам | 78,2 | 0,1478 |
| 20,4 | 0,0317 | |
| Железо | 78,2 | 0,0741 |
| 20,4 | 0,0076 | |
| Золото | 78,8 | 0,2189 |
| 20,4 | 0,0060 | |
| Медь | 81,6 | 0,1440 |
| 20,4 | 0,0008 | |
| Молибден | 77,8 | 0,1370 |
| 20,4 | 0,0448 | |
| Никель | 78,8 | 0,0919 |
| 20,4 | 0,0066 | |
| Олово | 79,0 | 0,2098 |
| 20,4 | 0,0116 | |
| Платина | 91,4 | 0,2500 |
| 20,4 | 0,0061 | |
| Ртуть | 90,1 | 0,2851 |
| 20,4 | 0,4900 | |
| Свинец | 73,1 | 0,2321 |
| 20,5 | 0,0301 | |
| Серебро | 78,8 | 0,1974 |
| 20,4 | 0,0100 | |
| Сурьма | 77,7 | 0,2041 |
| 20,4 | 0,0319 | |
| Хром | 80,0 | 0,1340 |
| 20,6 | 0,0533 | |
| Цинк | 83,7 | 0,2351 |
| 20,4 | 0,0087 |
Удельное сопротивление электролитов
В таблице даны значения удельного сопротивления электролитов в ом·см при температуре 18° С. Концентрация растворов с дана в процентах, которые определяют число граммов безводной соли или кислоты в 100 г раствора.
| c (%) | NH4Cl | NaCl | ZnSO4 | CuSO4 | КОН | NaOH | H2SO4 |
| 5 | 10,9 | 14,9 | 52,4 | 52,9 | 5,8 | 5,1 | 4,8 |
| 10 | 5,6 | 8,3 | 31,2 | 31,3 | 3,2 | 3,2 | 2,6 |
| 15 | 3,9 | 6,1 | 24,1 | 23,8 | 2,4 | 2,9 | 1,8 |
| 20 | 3,0 | 5,1 | 21,3 | — | 2,0 | 3,0 | 1,5 |
| 25 | 2,5 | 4,7 | 20,8 | — | 1,9 | 3,7 | 1,4 |
_______________
Источник информации: КРАТКИЙ ФИЗИКО-ТЕХНИЧЕСКИЙ СПРАВОЧНИК/ Том 1, — М.: 1960.
Свойства резистивных материалов
Удельное сопротивление металла зависит от температуры. Их значения приводится, как правило, для комнатной температуры (20°С). Изменение удельного сопротивления в результате изменения температуры характеризуется температурным коэффициентом.
Например, в термисторах (терморезисторах) это свойство используется для измерения температуры. С другой стороны, в точной электронике, это довольно нежелательный эффект.
Металлопленочные резисторы имеют отличные свойства температурной стабильности. Это достигается не только за счет низкого удельного сопротивления материала, но и за счет механической конструкции самого резистора.
Много различных материалов и сплавов используются в производстве резисторов. Нихром (сплав никеля и хрома), из-за его высокого удельного сопротивления и устойчивости к окислению при высоких температурах, часто используют в качестве материала для изготовления проволочных резисторов. Недостатком его является то, что его невозможно паять. Константан, еще один популярный материал, легко паяется и имеет более низкий температурный коэффициент.
Электрический заряд. Напряженность электрического поля
Напряженность поля наряду с электрическим зарядом является фундаментальным параметром в теории электричества. При этом количественное представление о них можно получить из простых опытов, доступных школьникам.
Для простоты рассуждений будем рассматривать электростатическое поле. Это электрическое поле, которое не изменяется со временем. Такое поле может быть создано неподвижными электрическими зарядами.
Также для наших целей необходим пробный заряд. В его качестве будем использовать заряженное тело — настолько малое, что оно не способно вызывать какие-либо возмущения (перераспределение зарядов) в окружающих объектах.
Рассмотрим поочередно два взятых пробных заряда, последовательно помещенных в одну точку пространства, находящуюся под воздействием электростатического поля. Получается, что заряды будут подвергаться неизменному во времени воздействию с его стороны. Пусть F1 и F2 — это силы, воздействующие на заряды.
В результате обобщения опытных данных было установлено, что силы F1 и F2 направлены либо в одну, либо в противоположные стороны, а их отношение F1/F2 является независимым от точки пространства, куда были поочередно помещены пробные заряды. Следовательно, отношение F1/F2 является характеристикой исключительно самих зарядов, и никак не зависит от поля.
Открытие данного факта позволило охарактеризовать электризацию тел и в дальнейшем было названо электрическим зарядом. Таким образом, по определению получается q1/q2 = F1/F2, где q1 и q2 — величина зарядов, помещаемых в одну точку поля, а F1 и F2 — силы, действующие на заряды со стороны поля.
Из подобных соображений были экспериментально установлены величины зарядов различных частиц. Условно положив в соотношение один из пробных зарядов равным единице, можно вычислить величину другого заряда, измерив соотношение F1/F2.
Через известный заряд можно охарактеризовать любое электрическое поле. Таким образом, сила, действующая на единичный пробный заряд, находящийся в состоянии покоя, называется напряженностью электрического поля и обозначается E. Из определения заряда получаем, что вектор напряженности имеет следующий вид: E = F/q.
Удельное сопротивление
Физический смысл удельного сопротивления в таблице имеет такую формулировку: величина «р» эквивалентна отношению сопротивления проводника из заданного материала в 1 Ом площадью поперечного сечения 1 мм 2 к длине 1 м. Математическая форма записи: p=/1м.
На основании общего соотношения можно вывести формулу удельного сопротивления: p=(RS)/L. Однако к этому физики пришли не сразу. После открытия закона Ома для полной цепи и ее участка применялись только три составляющих, а именно: сила тока, напряжение и сопротивление.
На протяжении определенного времени физики не могли понять различные измерения параметров (отклонения) в электрических схемах при постоянном напряжении и токе, которые фиксировались приборами. Оказалось, что причиной стала температура окружающей среды. Для обыкновенных металлов (золота, стали и никелина) величина сопротивления при высоком температурном коэффициенте увеличивалась, а при низком — уменьшалась.
Опытным путем был открыт новый параметр, зависящий не только от типа материала, но и от температуры. Его назвали удельным сопротивлением.
Проведение опыта
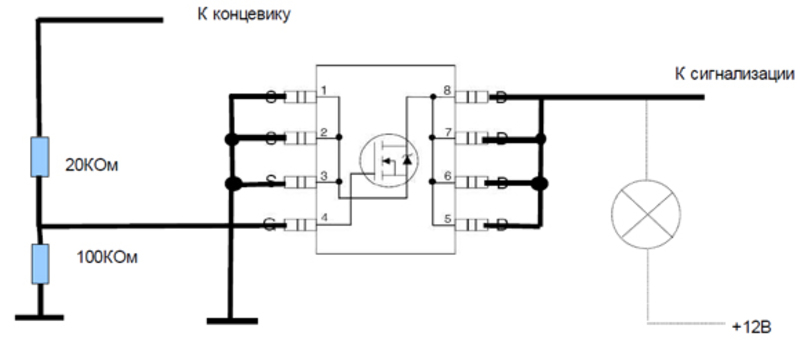
Опыт позволяет определить зависимость сопротивления от температуры. Для этого подойдет проволока из любого проводника (рекомендуется использовать никелин). Кроме того, понадобится источник питания, напряжение которого составляет примерно от 12 до 24 В постоянного тока. Далее необходимо собрать схему, дополнив ее лампой накаливания и выключателем. Элементы необходимо соединить последовательно.
После сборки схемы выключатель должен быть в положении «отключено». Если его включить, то лампочка будет гореть сначала ярко. Однако это будет длиться недолго — до нагрева спирали. Специалисты рекомендуют следить за техникой безопасности. Схему необходимо собирать, используя негорючие монтажные элементы.
Температурный коэффициент
Формула, связывающая сопротивление и температурный коэффициент выглядит таким образом: (R-R0)/R=at. Она состоит из следующий параметров:
- R0 — величины среднего значения сопротивления (при температуре по Цельсию 0 градусов).
- а — температурного коэффициента.
- t — температуры проводника.
Чтобы рассчитать температурный коэффициент, нужно найти опытным путем величину электросопротивления при нулевом значении температуры. Она измеряется при помощи прибора, который называется омметром. Далее требуется посчитать p через формулу «p=p0+aT».
Нахождение неизвестной величины р0 осуществляется по специальным таблицам, в которых ученые уже позаботились и измерили опытным путем параметр при температуре 20 градусов по Цельсию.
Таким образом, расчет сопротивления проводника производится не только по его геометрическим параметрам и веществу, из какого он состоит, а также по величине температуры.
Железо как проводник в электротехнике
Железо — самый распространенный в природе и технике металл (после водорода, который металлом тоже является). Он и самый дешевый, и имеет прекрасные прочностные характеристики, поэтому применяется повсюду как основа прочности различных конструкций.
В электротехнике в качестве проводника железо используется в виде стальных гибких проводов там, где нужна физическая прочность и гибкость, а нужное сопротивление может быть достигнуто за счет соответствующего сечения.
Имея таблицу удельных сопротивлений различных металлов и сплавов, можно посчитать сечения проводов, выполненных из разных проводников.
В качестве примера попробуем найти электрически эквивалентное сечение проводников из разных материалов: проволоки медной, вольфрамовой, никелиновой и железной. За исходную возьмем проволоку алюминиевую сечением 2,5 мм.
Нам нужно, чтобы на длине в 1 м сопротивление провода из всех этих металлов равнялось сопротивлению исходной. Сопротивление алюминия на 1 м длины и 2,5 мм сечения будет равно
Где R – сопротивление, ρ – удельное сопротивление металла из таблицы, S – площадь сечения, L – длина.
Подставив исходные значения, получим сопротивление метрового куска провода алюминия в омах.
После этого разрешим формулу относительно S
Будем подставлять значения из таблицы и получать площади сечений для разных металлов.
Так как удельное сопротивление в таблице измерено на проводе длиной в 1 м, в микроомах на 1 мм 2 сечения, то у нас и получилось оно в микроомах. Чтобы получить его в омах, нужно умножить значение на 10 -6 . Но число ом с 6 нулями после запятой нам получать совсем не обязательно, так как конечный результат все равно находим в мм 2 .
Как видим, сопротивление железа достаточно большое, проволока получается толстая.
Но существуют материалы, у которых оно еще больше, например, никелин или константан.
Про закон Ома многие слышали, но не все знают, что это такое. Изучение начинается со школьного курса физики. Более подробно проходят на физфаке и электродинамике. Рядовому обывателю эти знания маловероятно пригодятся, но они необходимы для общего развития, а кому-то для будущей профессии. С другой стороны, элементарные знания об электричестве, его устройстве, особенностей в домашних условиях помогут предостеречь себя от беды. Недаром закон Ома называют основным законом электричества. Домашнему мастеру нужно обладать знаниями в области электричества, чтобы не допустить перенапряжения, что может повлечь увеличению нагрузки и возникновению пожара.