Задачи на применение закона джоуля-ленца с решением

Опыты Ленца

Перенесемся в 19 век-эпоху накопления знаний и подготовки к технологическому прыжку 20 века. Эпоха, когда по всему миру различные учёные и просто изобретатели-самоучки чуть ли не ежедневно открывают что-то новое, зачастую тратя огромное количество времени на исследования и, при этом, не представляя конечный результат.

Один из таких людей, русский учёный Эмилий Христианович Ленц, увлекался электричеством, на тогдашнем примитивном уровне, пытаясь рассчитывать электрические цепи. В 1832 году Эмилий Ленц “застрял” с расчётами, так как параметры его смоделированной цепи “источник энергии – проводник – потребитель энергии” сильно разнились от опыта к опыту. Зимой 1832-1833 года учёный обнаружил, что причиной нестабильности является кусочек платиновой проволоки, принесённый им с холода. Отогревая или охлаждая проводник, Ленц также заметил что существует некая зависимость между силой тока, электрическим сопротивлением и температурой проводника.

При определённых параметрах электрической цепи проводник быстро оттаивал и даже слегка нагревался. Измерительных приборов в те времена практически никаких не существовало – невозможно было точно измерить ни силу тока, ни сопротивление. Но это был русский физик, и он проявил смекалку. Если это зависимость, то почему бы ей не быть обратимой?

Для того чтобы измерить количество тепла, выделяемого проводником, учёный сконструировал простейший “нагреватель” – стеклянная ёмкость, в которой находился спиртосодержащий раствор и погружённый в него платиновый проводник-спираль. Подавая различные величины электрического тока на проволоку, Ленц замерял время, за которое раствор нагревался до определённой температуры. Источники электрического тока в те времена были слишком слабы, чтобы разогреть раствор до серьёзной температуры, потому визуально определить количество испарившегося раствора не представлялось возможным. Из-за этого процесс исследования очень затянулся – тысячи вариантов подбора параметров источника питания, проводника, долгие замеры и последующий анализ.

https://youtube.com/watch?v=yP1V4Zzjl6Q

Магнитострикция

Параллельно со свойствами электрического тока Джеймс Джоуль изучает магнитные явления. В 1842 году он замечает, что железо изменяется в размерах под воздействием магнитных волн. Если металлические стержни поместить в магнитное поле, их длина станет чуть больше.

Научное сообщество сомневалось в существовании здесь какого-либо открытия. Изменение размеров стержней было настолько ничтожным, что человеческий глаз не улавливал его. Но физик разработал специальную технику, при помощи которой получил наглядные доказательства.

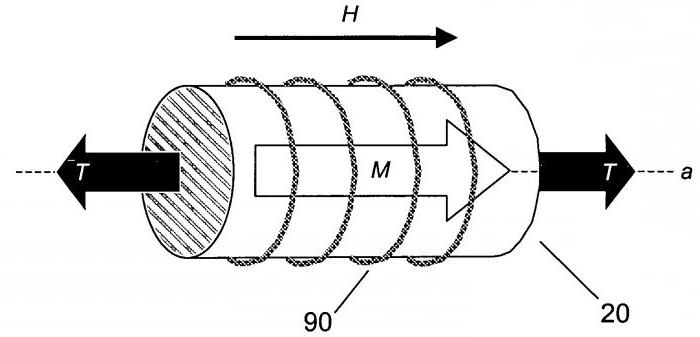
Позже выяснилось, что таким эффектом обладают и другие металлы, а само явление назвали магнитострикцией. Сейчас для открытия Джоуля нашли много способов применения. Например, материалом волновода для измерения уровня воды в резервуарах служат магнитострикционные металлы. Это явление используют и для изготовления меток в антикражевых системах.

Формула расчета и ее элементы

Суть явления понятна из упомянутого выше общего определения. Движущиеся электроны взаимодействуют с ионами вещества проводника с преобразованием механической энергии в теплоту. Увеличение силы тока повышает интенсивность процесса.

Наглядный пример – электролиз. При опускании в раствор подключенных к батарее пластин положительно заряженные ионы и электроны движутся в противоположных направлениях. Достаточно высокий ток провоцирует перемещение примесей с последующим осаждением на поверхности электродов. Одновременно происходит нагрев жидкости.

При подключении к источнику медного проводника химические реакции отсутствуют. Если исключить механические воздействия (электромагнитная индукция, движение ионов в растворе), вся работа тока в соответствующей цепи будет направлена только на увеличение внутренней энергии вещества.

Действие электрического тока при подключении к жидкому и металлическому проводнику

Следовательно, во втором примере работу (A) можно принять равной увеличению энергетического потенциала, который выражается соответствующим количеством теплоты (Q). Основная формула:

A = Q = U * I *t,

где:

U – напряжение;
I – ток;
t – время.

Для удобства расчетов можно использовать иные эквиваленты на основе формул закона Ома:

U = I * R;
R – электрическое сопротивление проводника;
значит, Q = I2 * R * t.

Интегральная и дифференциальная формулы

Формула ЭДС индукции

Установленные в предыдущем разделе зависимости справедливы при неподвижности проводника. В этом случае можно считать, что работа приложенных сторонних сил расходуется непосредственно на повышение температуры. С учетом заданной темы перемещение зарядов (q) обеспечивает разница потенциалов, которая эквивалентна напряжению (U = ϕ1 – ϕ2). Соответственно, A = q * (ϕ1 – ϕ2) = q * U. Заряд можно выразить через ток:

q = I*t.

После элементарных математических преобразований получится A = Q = I * U * t. Если взять изменение теплоты (dQ) за интервал времени (dt), можно составить выражение закона Джона Ленца в интегральной форме:

dQ = I2 * R * dt.

Для дальнейших рассуждений нужно ввести понятие плотности тепловой мощности (W). Этим термином обозначают количество энергии, которое выделяется за единицу времени в единичном объеме (V) контрольного проводника:

W = Q/(V*t).

Электрическое сопротивление можно выражать через удельный показатель (p):

R = p* (dL/dS),

где:

L – длина;
S – поперечное сечение.

Добавив плотность тока (j = IS = G *E) и понятие проводимости (G = 1/R), можно записать закон Ленца в дифференциальном виде следующим образом:

W = G * E2.

https://youtube.com/watch?v=GGnFhHSCuAs

https://youtube.com/watch?v=2qF52-fD_Ls

https://youtube.com/watch?v=dSx9Jihc200

Опыт Ленца

Для ответа на заданные вопросы проводится следующий опыт. На концах легко вращающегося коромысла закрепляются два проводящих кольца – одно сплошное, а другое с разрезом.

Рис. 1. Опыт демонстрирующий правило Ленца.

Теперь, если взять постоянный магнит и внести его в кольцо с разрезом – ничего не произойдет. Однако, если попытаться внести постоянный магнит в сплошное кольцо – коромысло начнет вращаться, уводя кольцо от магнита.

Данное явление можно объяснить только возникновением тока в сплошном кольце. Этот ток, в свою очередь, порождает новое магнитное поле, которое и начинает взаимодействовать с полем постоянного магнита. В кольце с разрезом ток не возникает, и взаимодействующего поля нет.

Признание Джеймса Джоуля

Слава и признание все же настигли английского физика. В 50-х годах XIX века он становится членом Лондонского королевского общества и награждается Королевской медалью. В 1866 году он получает медаль Копли, а затем и медаль Альберта.

Несколько раз Джоуль становился президентом Британской научной ассоциации. Ему были присуждены научные степени доктора права в дублинском колледже, Эдинбургском и Оксфордском университетах.

В его честь установлена статуя в здании муниципалитета в Манчестере и мемориал в Вестминстерском аббатстве. На обратной стороне Луны существует кратер Джеймса Джоуля.

Любознательным

Следы на песке

Если вам приходилось, гулять по пляжу во время отлива, то, вероятно,
вы заметили, что, как только нога ступает на мокрый твердый песок, он немедленно
подсыхает и белеет вокруг вашего следа. Обычно это объясняют тем, что под тяжестью тела
вода «выжимается» из песка. Однако это не так, потому что песок не ведет себя подобно мочалке.
Почему же белеет песок? Будет ли песок оставаться белым все время, пока вы стоите на месте?
Оказывается…
Побеление песка на пляже впервые объяснил Рейнольде в 1885 г. Он показал,
что объем песка увеличивается, когда на него наступают. До этого песчинки были «упакованы» самым плотным образом.
Под действием деформации сдвига, которая возникает под подошвой ботинка, объем, занимаемый песчинками, может
лишь увеличиться. В то время как уровень песка поднимается резко, уровень воды может подняться лишь в результате
капиллярных явлений, а на это требуется время. Поэтому на дне следа ноги песок некоторое время оказывается выше уровня воды —
он сухой и белый.

И это ещё не всё!

Почему греется проводник

Как же объясняется нагрев проводника? Почему он именно греется, а не остаётся нейтральным или охлаждается? Нагрев происходит из-за того, что свободные электроны, перемещающиеся в проводнике под действием электрического поля, бомбардируют атомы молекул металла, тем самым передавая им собственную энергию, которая переходит в тепловую. Если изъясняться совсем просто: преодолевая материал проводника, электрический ток как бы “трётся”, соударяется электронами о молекулы проводника. Ну а , как известно, любое трение сопровождается нагревом. Следовательно, проводник будет нагреваться пока по нему бежит электрический ток.

Из формулы также следует – чем выше удельное сопротивление проводника и чем выше сила тока протекающего по нему, тем выше будет нагрев . Например, если последовательно соединить проводник-медь (удельное сопротивление 0,018 Ом·мм²/м) и проводник-алюминий (0,027 Ом·мм²/м), то при протекании через цепь электрического тока алюминий будет нагреваться сильнее чем медь из-за более высокого сопротивления. Поэтому, кстати, не рекомендуется в быту делать скрутки медных и алюминиевых проводов друг с другом – будет неравномерный нагрев в месте скрутки. В итоге – подгорание с последующим пропаданием контакта.

https://youtube.com/watch?v=AhTBkQtk6qY

https://youtube.com/watch?v=jyfmcUiBPvg

Сохранение импульса

Импульс должен сохраняться в процессе, поэтому, если q 1 толкается в одном направлении, тогда q 2 должно толкаться в другом направлении с той же силой в то же время. Однако ситуация усложняется, когда вводится конечная скорость распространения электромагнитной волны (см. Запаздывающий потенциал ). Это означает, что в течение короткого периода общий импульс двух зарядов не сохраняется, а это означает, что разница должна объясняться импульсом в полях, как утверждал Ричард П. Фейнман . Известный электродинамик 19 века Джеймс Клерк Максвелл назвал это «электромагнитным импульсом». Тем не менее, такая трактовка полей может быть необходима, когда закон Ленца применяется к противоположным обвинениям. Обычно предполагается, что рассматриваемые заряды имеют один и тот же знак. Если они этого не делают, например, протон и электрон, взаимодействие будет другим. Электрон, создающий магнитное поле, будет генерировать ЭДС, которая заставляет протон ускоряться в том же направлении, что и электрон

Сначала может показаться, что это нарушает закон сохранения импульса, но такое взаимодействие, как видно, сохраняет импульс, если принять во внимание импульс электромагнитных полей.

Почему нагреваются проводники

Электрический ток — это упорядоченное движение заряженных частиц. В проводниках этими частицами выступают отрицательно заряженные электроны. Воздействие электрического поля сообщает электронам дополнительную кинетическую энергию. В процессе движения они сталкиваются с атомами (или молекулами) проводника, отдавая часть приобретенной энергии. По этой причине начинает увеличиваться внутренняя энергия вещества, что приводит к повышению температуры и выделению тепла.

Рис. 1. Электрический ток в проводнике нагревает проводник

Если взять обычную лампочку накаливания и подключить ее к источнику напряжения через реостат (переменное сопротивление), то можно наблюдать тепловой эффект от протекания тока. Постепенно увеличивая ток, мы можем сначала на ощупь почувствовать, что стеклянная колба лампочки постепенно начнет нагреваться, а затем увидим, как начинает светиться раскаленная нить накаливания.

Заметим, что в этом эксперименте подводящие провода сильно не нагреваются и не светятся. Это происходит потому, что сопротивление нити накаливания намного больше сопротивления подводящих проводов .

Как связаны свет и электричество?

Правильно лампочку называть лампой накаливания. Внутри в стеклянном корпусе расположена спираль из вольфрама. Электрический ток, проходя через эту спираль, раскаляет ее добела, и она начинает светиться. Вольфрам используется потому, что он обладает таким свойством – ярко светиться при нагревании. Металлическая нить сворачивается в спираль для того, чтобы увеличить длину нити, и, соответственно, количество получаемого света. Что касается устройства лампочки – разобрались. Все довольно просто. А вот почему вообще раскаляется спираль лампочки, и кто первым додумался это использовать?

Первые эксперименты с электричеством показали, что ток обладает тепловым действием. Он нагревает проводник, по которому идет. Величина нагревания зависит от вещества, из которого изготовлен проводник. Но какой-то нагрев происходит в любом случае. Обусловлено это тем, что отрицательно заряженные электроны, которые и представляют собой ток, при своем движении взаимодействуют с положительно заряженными ядрами кристаллической решетки, из которой состоит вещество проводника.

От этого взаимодействия уменьшается энергия электронов и увеличивается внутренняя энергия проводника. А от величины внутренней энергии и зависит температура вещества. Ток обладает еще магнитным и химическим действием. Если наш проводник неподвижен, и химического действия тока не происходит, то вся энергия, расходуемая током, идет на нагрев проводника. Энергия, израсходованная током, равна совершаемой током работе.

Детальное взаимодействие зарядов в этих токах

Алюминиевое кольцо перемещается за счет электромагнитной индукции, демонстрируя закон Ленца.

Эксперимент, демонстрирующий закон Ленца с двумя алюминиевыми кольцами на чешуйчатом устройстве, установленном на оси так, чтобы свободно перемещаться в горизонтальной плоскости. Одно кольцо полностью закрыто, а другое имеет отверстие, не образующее полный круг. Когда мы размещаем стержневой магнит около полностью замкнутого кольца оно отталкивается от него. Однако, когда система останавливается, и мы снимаем стержневой магнит, кольцо притягивается им. В первом случае индуцированный ток, создаваемый в кольце, сопротивляется увеличению магнитного потока, вызванному близостью магнита, в то время как во втором случае извлечение магнита из кольца уменьшает магнитный поток, вызывая такой ток, который магнитное поле сопротивляется уменьшению потока. Это явление отсутствует, когда мы повторяем эксперимент с кольцом, которое не закрывается, вставляя и удаляя стержень магнита. Индуцированные токи в этом кольце не могут замкнуться в кольце и имеют очень слабое поле, которое не может сопротивляться изменению магнитного потока.

В электромагнетизме, когда заряды движутся электрическое поле На них выполняется работа линий, будь то сохранение потенциальной энергии (отрицательная работа) или увеличение кинетической энергии (положительная работа).

Когда чистая положительная работа применяется к заряду q₁, он набирает скорость и импульс. Сеть работает на q₁ тем самым генерирует магнитное поле, напряженность которого (в единицах плотности магнитного потока (1 тесла = 1 вольт-секунда на квадратный метр)) пропорционально увеличению скорости q₁. Это магнитное поле может взаимодействовать с соседним зарядом q₂, передавая ему этот импульс, и взамен q₁ теряет динамику.

Заряд q₂ также может действовать на q₁ аналогичным образом, возвращая часть импульса, полученного от q₁. Этот возвратно-поступательный компонент импульса способствует магнитному индуктивность. Чем ближе q₁ и q₂ , тем больше эффект. Когда q₂ находится внутри проводящей среды, такой как толстая плита из меди или алюминия, она легче реагирует на приложенную к ней силу q₁. Энергия q₁ не расходуется мгновенно в виде тепла, выделяемого током q₂ но также хранится в два противодействующие магнитные поля. Плотность энергии магнитных полей имеет тенденцию изменяться в зависимости от квадрата напряженности магнитного поля; однако в случае магнитно-нелинейных материалов, таких как ферромагнетики и сверхпроводники, это ломается.

Практическое значение

Снижение потерь энергии

При передаче электроэнергии тепловое действие тока в проводах является нежелательным, поскольку ведёт к потерям энергии. Подводящие провода и нагрузка соединены последовательно — значит, ток в сети I{\displaystyle I} на проводах и нагрузке одинаков. Мощность нагрузки и сопротивление проводов не должны зависеть от выбора напряжения источника. Выделяемая на проводах и на нагрузке мощность определяется следующими формулами

Qw=Rw⋅I2,{\displaystyle Q_{w}=R_{w}\cdot I^{2},}

Qc=Uc⋅I.{\displaystyle Q_{c}=U_{c}\cdot I.}

Откуда следует, что Qw=Rw⋅Qc2Uc2{\displaystyle Q_{w}=R_{w}\cdot Q_{c}^{2}/U_{c}^{2}}. Так как в каждом конкретном случае мощность нагрузки и сопротивление проводов остаются неизменными и выражение Rw⋅Qc2{\displaystyle R_{w}\cdot Q_{c}^{2}} является константой, то тепло, выделяемое на проводе, обратно пропорционально квадрату напряжения на потребителе. Повышая напряжение, мы снижаем тепловые потери в проводах. Это, однако, снижает электробезопасность линий электропередачи.

Выбор проводов для цепей

Тепло, выделяемое проводником с током, в той или иной степени выделяется в окружающую среду. В случае, если сила тока в выбранном проводнике превысит некоторое предельно допустимое значение, возможен столь сильный нагрев, что проводник может спровоцировать возгорание находящихся рядом с ним объектов или расплавиться сам. Как правило, при выборе проводов, предназначенных для сборки электрических цепей, достаточно следовать принятым нормативным документам, которые регламентируют выбор сечения проводников.

Электронагревательные приборы

Если сила тока одна и та же на всём протяжении электрической цепи, то в любом выбранном участке будет выделять тепла тем больше, чем выше сопротивление данного участка.

За счёт сознательного увеличения сопротивления участка цепи можно добиться локализованного выделения тепла в этом участке. По этому принципу работают электронагревательные приборы. В них используется нагревательный элемент — проводник с высоким сопротивлением. Повышение сопротивления достигается (совместно или по отдельности) выбором сплава с высоким удельным сопротивлением (например, нихром, константан), увеличением длины проводника и уменьшением его поперечного сечения. Подводящие провода имеют обычное низкое сопротивление и поэтому их нагрев, как правило, незаметен.

Плавкие предохранители

Основная статья: Электрический предохранитель

Для защиты электрических цепей от протекания чрезмерно больших токов используется отрезок проводника со специальными характеристиками. Это проводник относительно малого сечения и из такого сплава, что при допустимых токах нагрев проводника не перегревает его, а при чрезмерно больших перегрев проводника столь значителен, что проводник расплавляется и размыкает цепь.

Тепловое действие тока

Электрический ток, проходя через любой проводник, сообщает ему некоторое количество энергии. В результате этого проводник нагревается. Передача энергии происходит на молекулярном уровне, т. е., электроны взаимодействуют с атомами или ионами проводника и отдают часть своей энергии.В результате этого, ионы и атомы проводника начинают двигаться быстрей, соответственно можно сказать, что внутренняя энергия увеличивается и переходит в тепловую энергию.Данное явление подтверждается различными опытами, которые говорят о том, что вся работа, которую совершает ток, переходит во внутреннюю энергию проводника, она в свою очередь увеличивается. После этого уже проводник начинает отдавать её окружающим телам в виде тепла. Здесь уже в дело вступает процесс теплопередачи, но сам проводник нагревается. Этот процесс рассчитывается по формуле: А=U·I·tА – это работа тока, которую он совершает, протекая через проводник. Можно также высчитать количество теплоты, выделяемое при этом, ведь это значение равно работе тока. Правда, это касается, лишь неподвижных металлических проводников, однако, такие проводники встречаются чаще всего. Таким образом, количество теплоты, также будет высчитываться по той же форме: Q=U·I·t.История открытия явленияВ своё время свойства проводника, через который протекает электрический тока, изучали многие учёные. Особенно среди них были заметны англичанин Джеймс Джоуль и русский учёный Эмилий Христианович Ленц. Каждый из них проводил свои собственные опыты, а вывод они смогли сделать независимо друг от друга. На основе своих исследований, они смогли вывести закон, который позволяет дать количественную оценку выделяемого тепла в результате воздействия электрического тока на проводник. Данный закон получил название «Закон Джоуля-Ленца». Джеймс Джоуль установил его в 1842 году, а примерно через год Эмиль Ленц пришёл к тому же выводу, при этом их исследования и проводимые опыты никак не были связаны друг с другом.Применение свойств теплового действия токаИсследования теплового воздействия тока и открытия закона Джоуля-Ленца позволили сделать вывод, подтолкнувший развитие электротехники и расширить возможности применения электричества. Простейшим примером применения данных свойства является простая лампочка накаливания. Устройство её заключается в том, что в ней применяется обычная нить накаливания, сделанная из вольфрамовой проволоки. Этот металл был выбран не случайно: тугоплавкий, он имеет довольно высокое удельное сопротивление. Электрический ток проходит через эту проволоку и нагревает её, т. е. передаёт ей свою энергию. Энергия проводника начинает переходить в тепловую энергию, а спираль разогревается до такой температуры, что начинает светиться. Главным недостатком такой конструкции, конечно, является то, что происходят большие потери энергии, ведь только небольшая часть энергии преобразуется в свет, а остальная уходит в тепло.Для этого вводится такое понятие в техники, как КПД, показывающее эффективность работы и преобразования электрической энергии. Такие понятия как КПД и тепловое воздействие тока применяются повсеместно, так как существует огромное количество приборов основанных подобном принципе. Это в первую очередь касается нагревательных приборов: кипятильников, обогревателей, электроплит и т. д.Как правило, в конструкциях перечисленных приборах присутствует некая металлическая спираль, которая и производит нагревание. В приборах для нагревания воды она изолирована, в них устанавливается баланс между потребляемой из сети энергией (в виде электрического тока) и тепловым обменом с окружающей средой.В связи с этим, перед учёными стоит нелёгкая задача по снижению потерь энергии, главной целью является поиск наиболее оптимальной и эффективной схемы. В данном случае тепловое воздействие тока является даже нежелательным, так как именно оно и ведёт к потерям энергии. Самым простым вариантом является повышение напряжения при передаче энергии. В результате снижается сила тока, но это приводит к снижению безопасности линий электропередач.Другое направление исследований – это выбор проводов, ведь от свойств проводника зависят и тепловые потери и прочие показатели. С другой стороны, различные нагревательные приборы требуют большого выделения энергии на определённом участке. Для этих целей изготавливают спирали из специальных сплавов. Для повышения защиты и безопасности электрических цепей применяются специальные предохранители. В случае чрезмерного повышения тока сечение проводника в предохранителе не выдерживает, и он плавится, размыкая цепь, защищая, таким образом, её от токовых перегрузок.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Силу тока в проводнике увеличили в 2 раза. Как изменится количество теплоты, выделяющееся в нём за единицу времени, при неизменном сопротивлении проводника?

1) увеличится в 4 раза
2) уменьшится в 2 раза
3) увеличится в 2 раза
4) уменьшится в 4 раза

2. Длину спирали электроплитки уменьшили в 2 раза. Как изменится количество теплоты, выделяющееся в спирали за единицу времени, при неизменном напряжении сети?

1) увеличится в 4 раза
2) уменьшится в 2 раза
3) увеличится в 2 раза
4) уменьшится в 4 раза

3. Сопротивления резистор \( R_1 \) в четыре раза меньше сопротивления резистора \( R_2 \). Работа тока в резисторе 2

1) в 4 раза больше, чем в резисторе 1
2) в 16 раз больше, чем в резисторе 1
3) в 4 раза меньше, чем в резисторе 1
4) в 16 раз меньше, чем в резисторе 1

4. Сопротивление резистора \( R_1 \) в 3 раза больше сопротивления резистора \( R_2 \). Количество теплоты, которое выделится в резисторе 1

1) в 3 раза больше, чем в резисторе 2
2) в 9 раз больше, чем в резисторе 2
3) в 3 раза меньше, чем в резисторе 2
4) в 9 раз меньше, чем в резисторе 2

5. Цепь собрана из источника тока, лампочки и тонкой железной проволоки, соединенных последовательно. Лампочка станет гореть ярче, если

1) проволоку заменить на более тонкую железную
2) уменьшить длину проволоки
3) поменять местами проволоку и лампочку
4) железную проволоку заменить на нихромовую

6. На рисунке приведена столбчатая диаграмма. На ней представлены значения напряжения на концах двух проводников (1) и (2) одинакового сопротивления. Сравните значения работы тока \( A_1 \) и \( A_2 \) в этих проводниках за одно и то же время.

1) \( A_1=A_2 \)
2) \( A_1=3A_2 \)
3) \( 9A_1=A_2 \)
4) \( 3A_1=A_2 \)

7. На рисунке приведена столбчатая диаграмма. На ней представлены значения силы тока в двух проводниках (1) и (2) одинакового сопротивления. Сравните значения работы тока \( A_1 \) и \( A_2 \) в этих проводниках за одно и то же время.

1) \( A_1=A_2 \)
2) \( A_1=3A_2 \)
3) \( 9A_1=A_2 \)
4) \( 3A_1=A_2 \)

8. Если в люстре для освещения помещения использовать лампы мощностью 60 и 100 Вт, то

А. Большая сила тока будет в лампе мощностью 100 Вт.
Б. Большее сопротивление имеет лампа мощностью 60 Вт.

Верным(-и) является(-ются) утверждение(-я)

1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б

9. Электрическая плитка, подключённая к источнику постоянного тока, за 120 с потребляет 108 кДж энергии. Чему равна сила тока в спирали плитки, если её сопротивление 25 Ом?

1) 36 А
2) 6 А
3) 2,16 А
4) 1,5 А

10. Электрическая плитка при силе тока 5 А потребляет 1000 кДж энергии. Чему равно время прохождения тока по спирали плитки, если её сопротивление 20 Ом?

1) 10000 с
2) 2000 с
3) 10 с
4) 2 с

11. Никелиновую спираль электроплитки заменили на нихромовую такой же длины и площади поперечного сечения. Установите соответствие между физическими величинами и их возможными изменениями при включении плитки в электрическую сеть. Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) электрическое сопротивление спирали
Б) сила электрического тока в спирали
B) мощность электрического тока, потребляемая плиткой

ХАРАКТЕР ИЗМЕНЕНИЯ
1) увеличилась
2) уменьшилась
3) не изменилась

12. Установите соответствие между физическими величинами и формулами, по которым эти величины определяются. Запишите в таблицу выбранные цифры под соответствующими буквами.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) работа тока
Б) сила тока
B) мощность тока

ФОРМУЛЫ
1) \( \frac{q}{t} \)
2) \( qU \)
3) \( \frac{RS}{L} \)
4) \( UI \)
5) \( \frac{U}{I} \)

Часть 2

13. Нагреватель включён последовательно с реостатом сопротивлением 7,5 Ом в сеть с напряжением 220 В. Каково сопротивление нагревателя, если мощность электрического тока в реостате составляет 480 Вт?

Электрическая дуга

Электрическая дуга является довольно эффективным преобразователем электрической энергии. Она используется при сварке металлических конструкций, а также служит мощным световым источником.

В основу устройства входит следующее. Берут два угольных стержня, подсоединяют провода и прикрепляют их в изолирующих держателях. После этого стержни подключают к источнику тока, который дает малое напряжение, но рассчитан на большую силу тока. Подключают реостат. Угли в городскую сеть включать запрещается, так как это может стать причиной пожара. Если коснуться одним углем о другой, то можно заметить, как сильно они раскалятся. Лучше не смотреть на это пламя, потому что оно вредно для зрения. Электрическую дугу используют в печах для плавки металла, а также в таких мощных осветительных приборах, как прожекторы, кинопроекторы и прочее.

Самоиндукция. Энергия магнитного поля

Самоиндукция является важным частным случаем электромагнитной индукции, когда изменяющийся магнитный поток, вызывающий ЭДС индукции, создается током в самом контуре. Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре.

Собственный Φ, пронизывающий контур или катушку с током, пропорционален силе тока I

Коэффициент пропорциональности L в этой формуле называется коэффициентом самоиндукциииндуктивностью катушки. Единица индуктивности в СИ называется генри (Гн). Индуктивность контура или катушки равна или 1 Гн, если при силе постоянного тока 1 А собственный поток равен 1 Вб

В качестве примера рассчитаем индуктивность длинного соленоида, имеющего N витков, площадь сечения S и длину l. Магнитное поле соленоида определяется формулой (см. § 1.17)

где I – ток в соленоиде, n = N / e – число витков на единицу длины соленоида.

Магнитный поток, пронизывающий все N витков соленоида, равен

Следовательно, индуктивность соленоида равна

где V = Sl – объем соленоида, в котором сосредоточено магнитное поле. Полученный результат не учитывает краевых эффектов, поэтому он приближенно справедлив только для достаточно длинных катушек. Если соленоид заполнен веществом с μ, то при заданном токе I индукция магнитного поля возрастает по модулю в μ раз (см. § 1.17); поэтому индуктивность катушки с сердечником также увеличивается в μ раз:

ЭДС самоиндукции, возникающая в катушке с постоянным значением индуктивности, согласно формуле Фарадея равна

ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней.

Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии. Если включить электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, то при размыкании ключа наблюдается кратковременная вспышка лампы (рис. 1.21.1). Ток в цепи возникает под действием ЭДС самоиндукции. Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.

Рисунок 1.21.1.
Магнитная энергия катушки. При размыкании ключа K лампа ярко вспыхивает.

Из закона сохранения энергии следует, что вся энергия, запасенная в катушке, выделится в виде джоулева тепла. Если обозначить через R полное сопротивление цепи, то за время Δt выделится количество теплоты ΔQ = I2RΔt.

Ток в цепи равен

Выражение для ΔQ можно записать в виде

В этом выражении ΔI < 0; ток в цепи постепенно убывает от первоначального значения I до нуля. Полное количество теплоты, выделившейся в цепи, можно получить, выполнив операцию интегрирования в пределах от I до 0. Это дает

Эту формулу можно получить графическим методом, изобразив на графике зависимость магнитного потока Φ(I) от тока I (рис. 1.21.2). Полное количество выделившейся теплоты, равное первоначальному запасу энергии магнитного поля, определяется площадью изображенного на рис. 1.21.2 треугольника.

Рисунок 1.21.2.
Вычисление энергии магнитного поля.

Таким образом, энергия W_м магнитного поля катушки с индуктивностью L, создаваемого током I, равна

Применим полученное выражение для энергии катушки к длинному соленоиду с магнитным сердечником. Используя приведенные выше формулы для коэффициента самоиндукции L_μ соленоида и для магнитного поля B, создаваемого током I, можно получить:

где V – объем соленоида. Это выражение показывает, что магнитная энергия локализована не в витках катушки, по которым протекает ток, а рассредоточена по всему объему, в котором создано магнитное поле. Физическая величина

равная энергии магнитного поля в единице объема, называется объемной плотностью магнитной энергии. Дж. Максвелл показал, что выражение для объемной плотности магнитной энергии, выведенное здесь для случая длинного соленоида, справедливо для любых магнитных полей.