Примеры применения
Допустимый ток для медных проводов — плотность тока в медном проводнике
В следующих разделах приведены описания задач, которые решают с помощью представленной методики. Следует подчеркнуть, что применение комплексных чисел пригодно для сложных расчетов с высокой точностью. Однако на практике достаточно часто сравнительно простой векторной графики с наглядным отображением исходной информации на одном рисунке.
Механика, гармонический осциллятор
Таким термином обозначают устройство, которое можно вывести из равновесного состояния. После этого система возвращается в сторону исходного положения, причем сила (F) соответствующего воздействия зависит от дальности первичного перемещения (d) прямо пропорционально. Величину ее можно уточнить с помощью постоянного корректирующего коэффициента (k). Отмеченные определения связаны формулой F=-d*k
Формулы для расчета основных параметров гармонического осциллятора
К сведению. Аналогичные процессы происходят в системах иной природы. Пример – создание аналога на основе электротехнического колебательного контура (последовательного или параллельного). Формулы остаются теми же с заменой соответствующих параметров.
Свободные гармонические колебания без затухания
Продолжая изучение темы на примерах механических процессов, можно отметить возможность построения двухмерной схемы. Скорость в этом случае на оси Х отображается так же, как и в одномерном варианте. Однако здесь можно учесть дополнительно фактор ускорения, которое направляют под углом 90° к предыдущему вектору.
Гармонический осциллятор с затуханием и внешней вынуждающей силой
В этом случае также можно воспользоваться для изучения взаимного влияния дополнительных факторов векторной графикой. Как и в предыдущем примере, скорость и другие величины представляют в двухмерном виде. Чтобы правильно моделировать процесс, проверяют суммарное воздействие внешних сил. Его направляют к центру системы (точке равновесия). С применением геометрических формул вычисляют амплитуду механических колебаний после начального воздействия с учетом коэффициента затухания и других значимых факторов.
Расчет электрических цепей
Векторную графику применяют для сравнительно несложных цепей, которые созданы из набора элементов линейной категории: конденсаторы, резисторы, катушки индуктивности. Для более сложных схем пользуются методикой расчета «Комплексных амплитуд», в которой реактивные компоненты определяют с помощью импедансов.
Векторная диаграмма для схемы соединений без нейтрального провода – звезда
Векторная диаграмма в данном случае выполняет функцию вспомогательного чертежа, который упрощает решение геометрических задач. Для катушек и конденсаторов, чтобы не пользоваться комплексным исчислением, вводят специальный термин – реактивное сопротивление. При синусоидальном токе изменение напряжения на индуктивном элементе описывается формулой U=-L*w*I0sin(w*t+f0).
Несложно увидеть подобие с классическим законом Ома. Однако в данном примере изменяется фаза. По этому параметру на конденсаторе напряжение отстает от тока на 90°. В индуктивности – обратное распределение. Эти особенности учитывают при размещении векторов на рисунке. В формуле учитывается частота, которая оказывает влияние на величину этого элемента.
Схемы и векторные диаграммы для идеального элемента и диэлектрика с потерями
Преобразование Фурье
Векторные технологии применяют для анализа спектров радиосигналов в определенном диапазоне. Несмотря на простоту методики, она вполне подходит для получения достаточно точных результатов.
Сложение двух синусоидальных колебаний
В ходе изучения таких источников сигналов рекомендуется работать со сравнительно небольшой разницей частот. Это поможет создать график в удобном для пользователя масштабе.
Фурье-образ прямоугольного сигнала
В этом примере оперируют суммой синусоидальных сигналов. Последовательное сложение векторов образует многоугольник, вращающийся вокруг единой точки. Для правильных расчетов следует учитывать отличия непрерывного и дискретного распределения спектра.
Для этого случая пользуются тем же отображением отдельных синусоид в виде векторов, как и в предыдущем примере. Суммарное значение также вписывается в окружность.
⇡#Inkscape — полноценная альтернатива коммерческим пакетам
Векторный редактор Inkscape имеет массу достоинств. Во-первых, он кроссплатформенный (может запускаться в среде Windows, Linux, Mac). Во-вторых, он поддерживает большое число популярных векторных форматов, в числе которых SVG, SVGZ, EMF, DXF, EPS, PostScript, WMF и другие.
В редакторе есть и стандартные для любого векторного редактора средства для создания графики: формы, кривые, текст, заливка, полноценная поддержка слоев. Inkscape дает возможность выполнять различные действия с контурами, делать обводку, а также применять булевы операции (объединять, пересекать элементы, исключать один из другого и так далее). В распоряжении пользователя большая библиотека фильтров и специальный редактор, при помощи которого можно создавать собственные эффекты. В программе реализована поддержка графических планшетов, благодаря чему в ней можно вручную рисовать, управляя наклоном и силой нажатия пера.
Стоит обратить внимание на встроенные средства для векторизации растровых изображений. Чтобы при трассировке фотографий учитывались важные объекты на переднем плане, задействуется алгоритм SIOX (Simple Interactive Object Extraction), помогающий определить такие объекты автоматически
Lucidchart.com
Это онлайн-сервис создания диаграмм, который позволяет визуализировать данные вместе с командой. Интерфейс понятный, поэтому создать диаграмму можно за несколько минут — можно выбрать среди множества готовых шаблонов, или же начать с чистого листа. Имея бесплатный тариф, вы получаете доступ к основным фигурам, стрелкам и текстовым полям. Готовые диаграммы можно сохранять форматах JPEG, PDF, PNG, SVG и Visio (VDX). Если используете бесплатную учетную запись, то получаете 25 МБ хранилища и возможность создать до 5 диаграмм.
Особенности Lucidchart:
- Интуитивно понятный пользовательский интерфейс.
- Интеграция с Google Apps, Confluence, JIRA, Office 365.
- Сотрудничество с коллегами в режиме реального времени с помощью общего доступа.
- Сохранение документов в форматах PDF, JPG, PNG.
- Десятки типов диаграмм и шаблонов для их создания.
Построение векторной диаграммы напряжений и токов
Последовательное и параллельное соединение аккумуляторов
Для изучения технологии выберем однофазный источник синусоидального напряжения (U). Ток изменяется по формуле I=Im*cos w*t. Подключенная цепь содержит последовательно подключенные компоненты со следующими значениями:
- резистор: Ur=Im*R*cos w*t;
- конденсатор: Uc=Im*Rc*cos (w*t-π/2), Rc=1/w*C;
- катушка: UL= Im*RL*cos(w*t+π/2), RL=w*L.
При прохождении по цепи переменного тока на реактивных элементах будет соответствующий сдвиг фаз. Чтобы построить вектора правильно, рассчитывают амплитуды и учитывают изменение направлений. Ниже приведена последовательность создания графики вручную.
Диаграмма напряжений и токов на отдельных элементах
Далее с применением элементарных правил геометрии проверяют взаимное влияние векторов.
Решение векторного уравнения
На первом рисунке приведен результат сложения двух векторов при условии, когда Uc меньше UL. Добавив значение на сопротивление, получим результирующее напряжение Um. На третьей иллюстрации отмечен общий фазовый сдвиг.
Векторное отображение процессов в параллельном колебательном контуре, резонанс напряжений
В топографической диаграмме начало координат совмещают с так называемой точкой «нулевого потенциала». Такое решение упрощает изучение отдельных участков сложных схем.
Специализированный редактор онлайн
В интернете можно найти программу для построения векторных диаграмм в режиме online.
https://youtube.com/watch?v=Jdj-seyl74Y
§ 1.13. Внешняя характеристика трансформатора
При колебаниях
нагрузки трансформатора его вторичное
напряжение
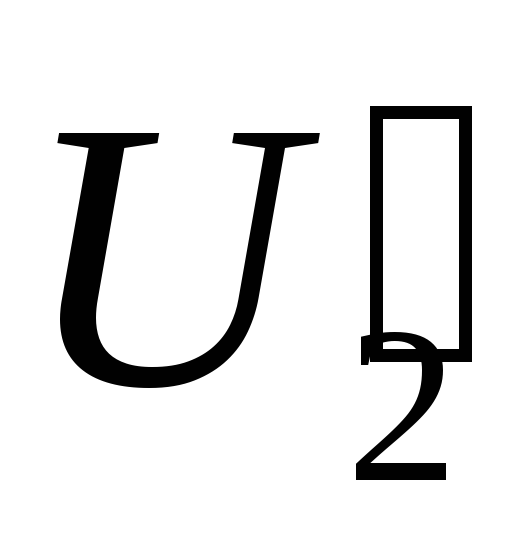

Измерение
вторичного напряжениятрансформатора
при увеличении нагрузки от х.х. до
номинальной является важнейшей
характеристикой трансформатора и
определяется выражением
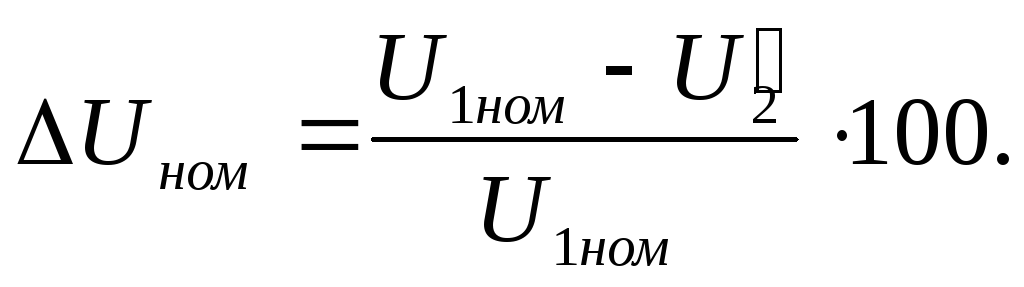 (1.67)
(1.67)
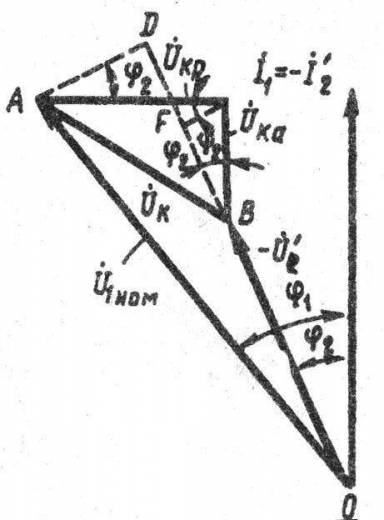
Рис.
1.37. К выводу формулы
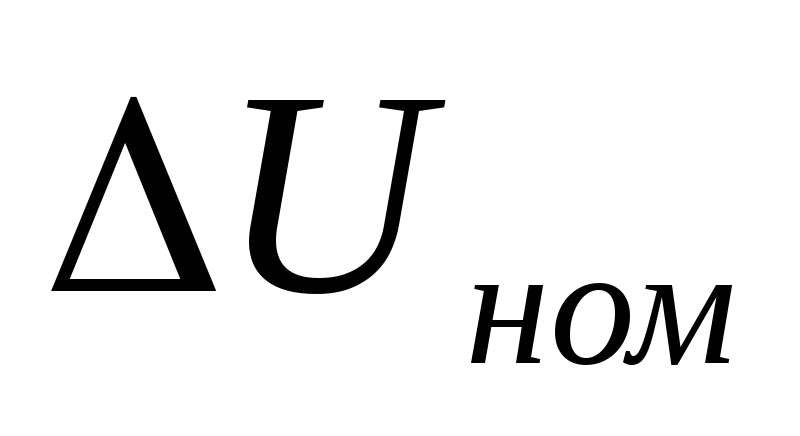
Для определения
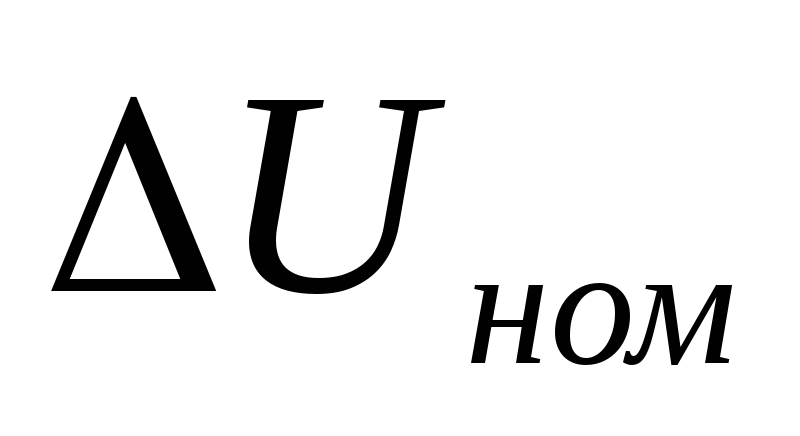
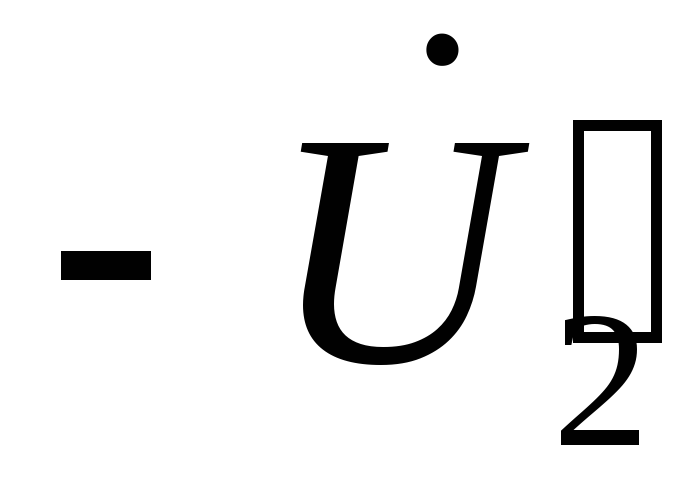
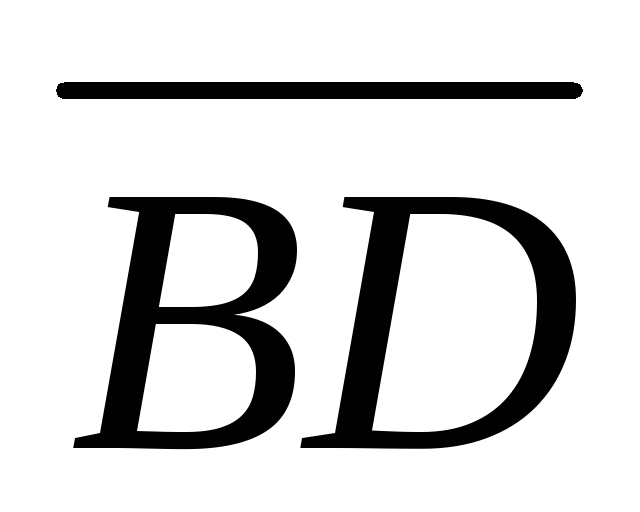
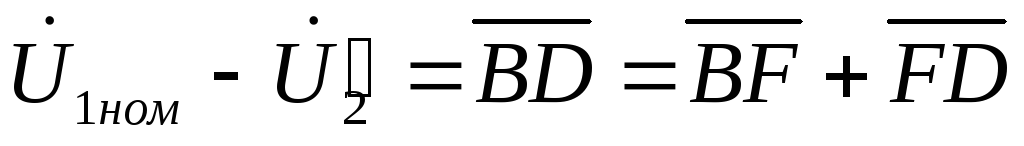
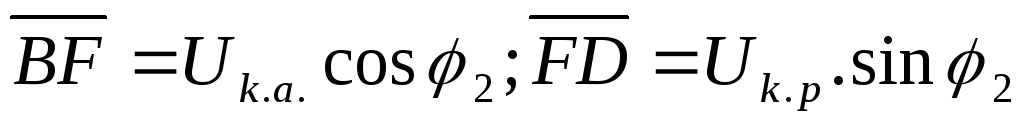
 (1.68.)
(1.68.)
Измерение вторичного
напряжения (1.67) с учетом (1.68) примет вид
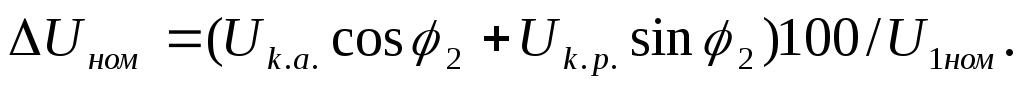 (1.69)
(1.69)
Обозначим
(Uk.a./U1ном)100=Uk.a.;
(Uk.p./U1ном)100=Uk.p.,
тогда выражение изменения вторичного
напряжения трансформатора при увеличении
нагрузки примет вид
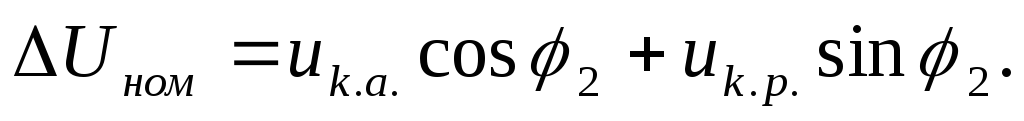 (1.70)
(1.70)
Выражение (1.70) дает
возможность определить изменение
вторичного напряжения лишь при номинальной
нагрузке трансформатора. При необходимости
расчета измерение вторичного напряжения
для любой нагрузки в выражение (1.70)
следует ввести коэффициент нагрузки,
представляющий собой относительное
значение тока нагрузки=I2/I2ном
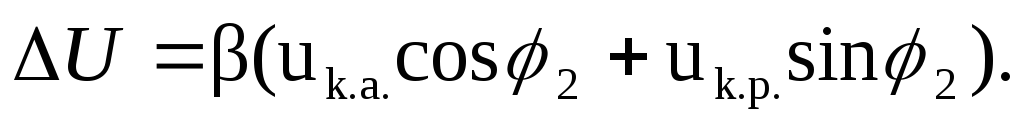 (1.71)
(1.71)
из выражения (1.71)
следует, что изменение вторичного
напряжения
 2
2
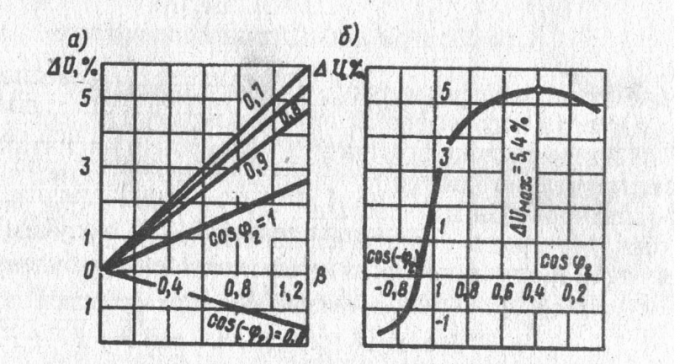
Рис. 1.38. Зависимость
 rr
rr
На рис. 1.38, а
представлен график зависимости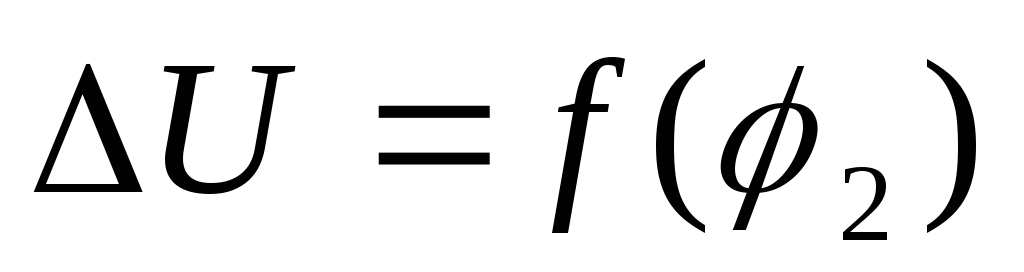 при cos2=const,
при cos2=const,
а на рис. 1.38, б – график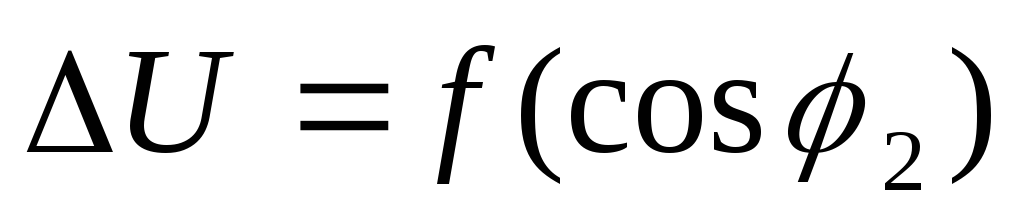 при=const.
при=const.
На этих графиках отрицательные значения

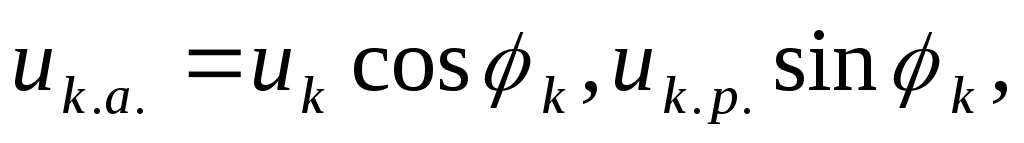
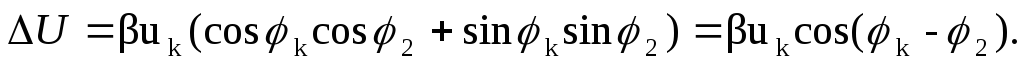 (1.72)
(1.72)
Из (1.72) следует,
что наибольшее значение изменения
напряжения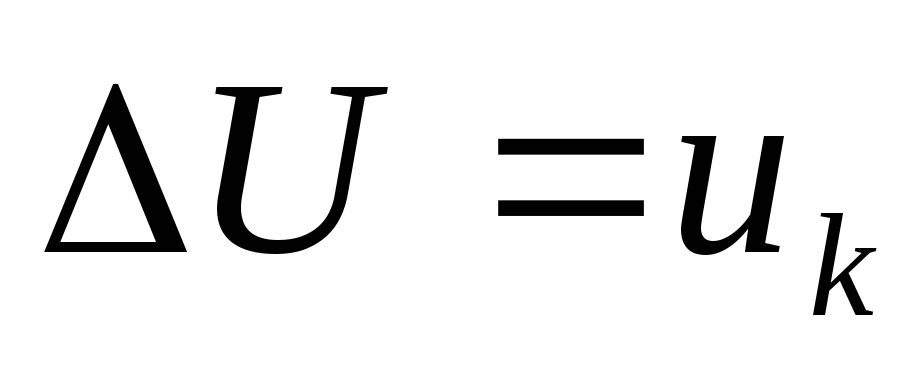 имеет место при равенстве углов фазового
имеет место при равенстве углов фазового
сдвига2=к,
тогдаcos(k-2)=1.
Зависимость
вторичного напряжения
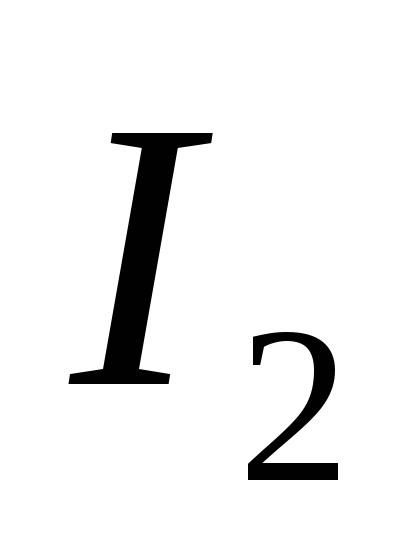 внешней характеристикой
внешней характеристикой
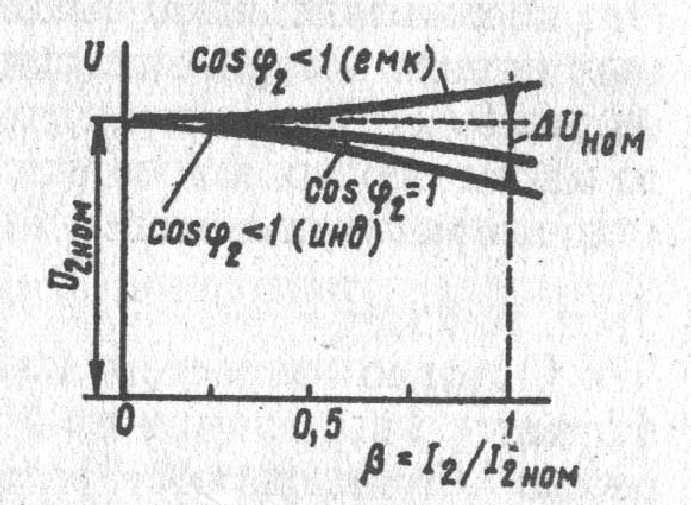
Рис. 1.39. Внешние
характеристики трансфоматора.
Вид внешней
характеристики (рис. 1.39) зависит от
характера нагрузки трансформатора
(cos2).
Внешнюю характеристику трансформатора
можно построить по (1.72) путем расчета
 2
2
Пример
1.6. Для
трансформатора, данные которого приведены
в примерах 1.4 и 1.5, (см. §
1.11.),
определить изменение вторичного
напряжения при номинальной нагрузке
(=1)
с коэффициентом мощности cos2
= 1,8 для нагрузок двух характеров:
активно-индуктивной и ативно-емкостной.
Решение.
Из
примера 1.4 имеем: uk75
=5,4%; cosφk75=0,4;
sinφk75
=0,92 . По
(1.72) при cosφ2
= 0,8 и sinφ2
= 0,6 получим:
для
активно-индуктивной нагрузки
∆U=5,4(0,4•0,8+0,92•0,6)=4,65%;
для
активно-емкостной нагрузки
∆U=5,4=-1,2%.
В
результате аналогичных расчетов,
проделанных при β=0÷1,2, для нагрузок с
cosφ2,
равным 0,7; 0,8; 0,9 и 1,0, получены данные, по
которым построены графики ∆U
= f(β),
представленные на рис 1 38, а.
Наибольшее
изменение напряжения соответствует
активно-индуктивной нагрузке
с cosφ2
= cosφk75
= 0,40 и коэффициенту нагрузки β = 1
(перегрузка трансформатора недопустима)
∆U
тax=
uk75=
5,4% (см рис. 1.38,6)
Подготовка данных для лучевой диаграммы
Как уже упоминалось выше данный шаблон будет обладать возможностью визуального построения связей до 20-ти участников (компаний, филиалов, контрагентов и т.п.). На листе книги шаблона «Данные» предоставленная таблица для заполнения входящих значений. Например, заполним ее для 14-ти участников рынка:
На этом же листе создадим дополнительную таблицу, которая представляет собой матрицу связей всех возможных участников, сгенерированную формулой:
С подготовкой данных мы закончили переходим к обработке.
Как вычислить сумму векторов?
Вектора и матрицы в электронной таблице хранятся в виде массивов.
Известно, что сумма векторов – это вектор, координаты которого равны суммам соответствующих координат исходных векторов:
Для вычисления суммы векторов нужно выполнить следующую последовательность действий:
– В диапазоны ячеек одинаковой размерности ввести значения числовых элементов каждого вектора.
– Выделить диапазон ячеек для вычисляемого результата такой же размерности, что и исходные векторы.
– Ввести в выделенный диапазон формулу перемножения диапазонов
– = Адрес_Вектора_1 + Адрес_Адрес_Вектора_2
– Нажать комбинацию клавиш + +.
Пример.
Даны два вектора:
Требуется вычислить сумму этих векторов.
Решение:
– В ячейки диапазона А2:A4
введем значения координат вектора a1, а в ячейки диапазонаС2:С4 – координаты вектора a2.
– Выделим ячейки диапазона, в которых будет вычисляться результирующий вектор С (E2:E4
) и введем в выделенный диапазон формулу:
=A2:A4+C2:C4
– Нажмем комбинацию клавиш + +. В ячейках диапазона E2:E4
будут вычислены соответствующие координаты результирующего вектора.
Заказать решение ТОЭ
- Метрология Электрические измерения
- Пигарев А.Ю. РГЗ по электротехнике и электронике в Multisim
- Теория линейных электрических цепей ТЛЭЦ — Теория линейных электрических цепей железнодорожной автоматики, телемеханики и связи: задание на контрольные работы № 1 и 2 с методическими указаниями для студентов IV курса специальности Автоматика, телемеханика и связь на железнодорожном транспорте — Контрольная работа №1
- — Контрольная работа №2
Электротехника и основы электроники
- — Электротехника и основы электроники: Методические указания и контрольные задания для студентов-заочников инженерно-технических специальностей высших учебных заведений / Соколов Б.П., Соколов В.Б. – М.: Высш. шк., 1985. – 128 с, ил — Контрольная работа № 1 Электрические цепи
— Контрольная работа № 2 Трансформаторы и электрические машины
— Контрольная работа № 3 Основы электроники
Теоретические основы электротехники ТОЭ
- — Артеменко Ю.П., Сапожникова Н.М. Теоретические основы электротехники: Пособие по выполнению курсовой работы МГТУ ГА 2009
— Переходные процессы Переходные процессы в электрических цепях
— Теоретические основы электротехники Методические указания и контрольные задания для студентов технических специальностей вузов — Задание 1 Линейные электрические цепи постоянного и синусоидального тока — Задача 1.1 Линейные электрические цепи постоянного тока
— Задача 1.2 Линейные электрические цепи синусоидального тока
— Задание 2 Четырехполюсники, трехфазные цепи, периодические несинусоидальные токи, электрические фильтры, цепи с управляемыми источниками
— Теоретические основы электротехники сб. заданий Р.Я. Сулейманов Т.А. Никитина Екатеринбург УрГУПС 2010
— Трехфазные цепи. Расчет трехфазных цепей
— УГТУ-УПИ Решение ТОЭ Билеты по ТОЭ
— Электромагнитное поле Электростатическое поле Электростатическое поле постоянного тока в проводящей среде Магнитное поле постоянного тока
Советуем изучить Основные химические источники электроэнергии
https://youtube.com/watch?v=5FtG-VD3hhw
Векторная диаграмма
Векторная иллюстрация Представляя синусоидальные токи, напряжения и ЭДС в комплексных числах, они могут быть представлены на комплексной плоскости в виде векторов и в виде соответствующей векторной диаграммы, для процесса расчета схемы, для этих чисел Может быть отображено.
Это один из основных инструментов для анализа электрических цепей, они четко иллюстрируют процесс решения проблемы, качественно контролируют и легко устанавливают квадрант, в котором находится нужный вектор.
Диаграмма вектора тока и напряжения 1 Для удобства при построении диаграммы статический вектор анализируется в определенный момент времени. Это выбрано так, чтобы диаграмма была в легко понятном формате.
Ось OX соответствует реальному значению, а ось OY соответствует мнимой оси (мнимая единица). Синусоида указывает, что конечная точка проекции перемещается к оси OY.
Каждое напряжение и ток соответствуют собственному вектору на полярной плоскости. Его длина отображает текущее значение амплитуды, а угол равен фазе. Вектор, изображенный на такой диаграмме, характеризуется равной угловой частотой ω. Во время вращения их относительные положения не меняются.
Таким образом, векторная диаграмма дает четкое представление о различных электрических выводах или наконечниках. В основном, векторные диаграммы представляют фактические значения, а не амплитуды. Вектор действительных значений количественно отличается от значения амплитуды.
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
Векторная графика — хороший способ правильно отобразить переменные, которые определяют функции беспроводного устройства. Это означает соответствующее изменение основных параметров сигнала в соответствии со стандартной синусоидальной (косинусоидальной) кривой. В визуальном представлении процесса гармонические колебания представлены в виде векторных проекций на оси координат.
- Вы можете легко рассчитать длину по стандартной формуле. Это равно амплитуде в определенный момент времени.
- Угол наклона указывает на фазу.
- Общий эффект и соответствующее изменение вектора следуют нормальным правилам геометрии.
- Различают графики высокого качества и точные графики.
Первый используется для объяснения взаимосвязей. Они полезны для проведения предварительных оценок и используются для полной замены расчетов. Другие создаются с учетом результатов, полученных для определения размера и ориентации отдельных векторов.
Решение задач по электротехнике тоэ
| Комплексные сопротивление и проводимость | Треугольники сопротивлений, проводимостей, мощностей, напряжений и токов |
| Мощность в цепи синусоидального тока | Расчет цепей с взаимными индуктивностями |
4.6.ЭКВИВАЛЕНТНАЯ СХЕМА ТРАНСФОРМАТОРА
Одним из методических приемов, облегчающих исследование электромагнитных процессов и расчет трансформаторов, является замена реального трансформатора с магнитными связями между обмотками эквивалентной электрической схемой (рис. 4.6.1).
На этом рисунке представлена эквивалентная схема приведенного трансформатора, на которой сопротивления г и х условно вынесены из соответствующих обмоток и включены с ними последовательно. Т.к. k = 1, то E1 = E2. Поэтому точки А и а, а также Х и х на приведенном трансформаторе имеют одинаковые потенциалы, что позволит электрически соединить эти точки, получив Т-образную эквивалентную схему замещения (рис. 4.6.2).
Произведя математическое описание этой схемы методами Кирхгофа, можно сделать вывод о том, что она полностью соответствует уравнениям ЭДС и токов реального трансформатора (см. раздел 4.5). Отсюда появляется возможность электрического моделирования трансформатора на ЭВМ. Проводя исследования относительно нагрузки z2′ (единственного переменного параметра схемы), можно прогнозировать реальные ха-рактеристики трансформатора, начиная от холостого хода (z2’= ) и кончая коротким замыканием (z2′ = 0).
Мощность цепи с конденсатором
Выражение мгновенной мощности реального конденсатора
p = ui = Umsinωt * Imsin(ωt+φ)
совпадает с выражением мгновенной мощности катушки. Рассуждения, аналогичные тем, которые сделаны при рассмотрении графика мгновенной мощности катушки (см. рис.13. 11), можно провести и для реального конденсатора на основе графика рис. 13.17. Величины активной, реактивной и полной мощностей выражаются теми же формулами, какие были получены для катушки . Это нетрудно показать, если стороны треугольника токов, выраженные в единицах тока, умножить на напряжение U. В результате умножения получится подобный треугольник мощностей (рис. 13.16, в), катетами которого являются мощности; активная
P = UIG = UIcosφ
реактивная
Q = UIC = UIsinφ
полная
Что такое векторная диаграмма токов и напряжений? Как построить график
Использование векторных диаграмм при анализе, расчете цепей переменного тока делает возможным рассмотреть более доступно и наглядно происходящие процессы, а также в некоторых случаях значительно упростить выполняемые расчеты.
Векторной диаграммой принято называть геометрическое представление изменяющихся по синусоидальному (либо косинусоидальному) закону направленных отрезков — векторов, отображающих параметры и величины действующих синусоидальных токов, напряжений либо их амплитудных величин.
Различают 2-х вида векторных диаграмм:
- точные;
- качественные.
Интересное видео о векторных диаграммах смотрите ниже:
Точные изображаются по результатам численных расчетов при условии соответствия масштабов действующих значений. При их построении можно геометрически определить фазы и амплитудные значения искомых величин.
Они являются одним из основных средств анализа электрических цепей, позволяя наглядно иллюстрировать и качественно контролировать ход решения задачи и легко установить квадрант, в котором располагается искомый вектор.
Для удобства при построении диаграмм анализируют неподвижные векторы для определенного момента времени, который выбирается таким образом, чтобы диаграмма имела удобный для понимания вид. Ось OХ соответствует величинам действительных чисел, ось OY — оси мнимых чисел (мнимая единица). Синусоида отображает движение конца проекции на ось OY. Каждому напряжению и току соответствует собственный вектор на плоскости в полярных координатах. Его длина отображает амплитудное значение величины тока, при этом угол равен фазе.
Векторы, изображаемые на такой диаграмме, характеризуются равновеликой угловой частотой ω. В виду чего при вращении их взаимное расположение не изменяется.
Ещё одно полезное видео о векторных диаграммах:
А остальные — изображать по отношению к исходному под различными углами, соответственно равными углам сдвига фаз.
Таким образом, векторная диаграмма дает отчетливое представление об опережении либо отставании различных электрических величин. Допустим у нас есть ток, величина которого изменяется по некоторому закону:
i = Im sin (ω t + φ).
С начала координат 0 под углом φ проведем вектор Im, величина которого соответствует Im. Его направление выбирается так, чтобы с положительным направлением оси OX вектор составлял угол — соответствующий фазе φ.
В основном векторные диаграммы изображают для действующих значений, а не амплитудных. Векторы действующих значений количественно отличаются от амплитудных значений — масштабом, поскольку:
Схема включения однофазного трансформатора напряжения
Рисунок 2.3. Векторная диаграмма трансформатора тока с активно-индуктивной вторичной нагрузкой Построение начинается с вектора вторичного тока İ
2, направление которого выбирается произвольно (в нашем случае по оси ординат). Вторичная ЭДС при вторичной активно-индуктивной нагрузкеE 2 =R 2I 2 +jX2 I 2 опережает вектор токаİ 2 на угол ; а ЭДСE 2 опережает потокФ – на угол 90 о .
Ток намагничивания İ
, приведенный также к вторичной обмотке,опережает поток на угол потерь в стали . Первичный токİ 1 получают путём векторного суммирования векторов токовİ 2 иİ .
Величина вторичного тока зависит от кратности первичного тока ( — номинальный первичный ток ИТТ) и сопротивления нагрузки .
С увеличением и вторичный ток уменьшается по сравнению со значением İ
1 из-за увеличения намагничивающего токаİ . Допустимая погрешность трансформации обеспечивается работой ИТТ в режиме, близком к короткому замыканию вторичной обмотки , т.е. с небольшим. При размыкании вторичной обмоткиİ 1 =İ , поток резко возрастает и мгновенные значения ЭДС во вторичной обмотке могут оказаться недопустимо большими, что может вызвать пробой изоляции обмотки и выход из строя ИТТ.Поэтому при протекании тока по первичной обмотке ИТТ вторичную обмотку нельзя размыкать . При необходимости замены измерительного прибора или реле вторичная обмотка ИТТ предварительнонакоротко замыкается (или шунтируется обмотка реле, прибора).
При выполнении релейной защиты схемы цепей тока строятся так, чтобы была обеспечена необходимая её чувствительность при использовании наименьшего количества оборудования. По числу фаз, в которые включены используемые в схеме ИТТ, различают: трёхфазные схемы
(ИТТ включены в три фазы) идвухфазные (ИТТ включены в две фазы), которые могут использоваться лишь в защитах от многофазных КЗ. Основные схемы соединения обмоток ИТТ приведены на рис. 2.4 (здесьИОi – измерительные органы — токовые обмотки реле).
Рисунок 2.4. Схемы соединения обмоток ИТТ(а
– схема полной звезды,б – схема соединения с полным треугольником,в — схема соединения ИТТ в фильтр токов нулевой последовательности)
Схема полной звезды – трёхфазная, трёхрелейная (рис. 2.4, а
) – может быть использована в защитах от всех видов многофазных и однофазных замыканий.
Соединение ИТТ полным треугольником – трёхфазная, трёхрелейная — (рис. 2.4, б
) – может быть использована в защитах от всех видов многофазных и однофазных замыканий.
Соединение ИТТ в фильтр токов нулевой последовательности (рис. 2.4, в
). ИТТ устанавливаются в трёх фазах, одноимённые зажимы соединяются параллельно.
Измерительные трансформаторы напряжения
ИТН выполняют в виде двухобмоточного понижающего трансформатора. Схема подключения однофазного трансформатора напряжения показана на рис. Для обеспечения безопасности работы обслуживающего персонала вторичную обмотку заземляют. Условное обозначение трансформатора напряжения такое же, как двухобмоточного трансформатора.
Схема включения однофазного трансформатора напряжения
Особенностью работы ИТН является режим близкий к холостому ходу его вторичной цепи. Первичная обмотка ИТН с числом витков включается на напряжение сети .
В режиме холостого хода под действием напряжения по обмотке протекает намагничивающий ток , создающий в магнитопроводе магнитный поток . Магнитный поток, в свою очередь, наводит в первичной и вторичной обмотках ЭДС с действующими значениями соответственно
Откуда получаем следующее отношение:
где — коэффициент трансформации ИТН.
В режиме холостого хода ток , а ток в первичной обмотке равен току намагничивания . При этом и напряжение незначительно отличается от ЭДС . Следовательно,
Работа ИТН с нагрузкой сопровождается протеканием тока и увеличением (по сравнению с холостым ходом) тока . Появление тока во вторичной обмотке увеличивает первичный ток по сравнению с током холостого хода на величину, пропорциональную вторичному току . Вторичный ток как бы проходит через первичную цепь с соответствующим пересчётным множителем .
Читайте та