Учёт эффекта в технике и борьба с ним
Скин-эффект проявляется существеннее с увеличением частоты переменного тока, и учитывается при конструировании и расчётах электрических схем, работающих на переменном и импульсным током. Так как ток высокой частоты течёт по тонкому поверхностному слою проводника, общее активное сопротивление проводника возрастает, что приводит к быстрому затуханию колебаний высокой частоты.
Скин-эффект влияет на характеристики катушек индуктивности и колебательных контуров, такие как добротность, на затухание в линиях передачи, на характеристики фильтров, на расчёты тепловых потерь и КПД, на выбор сечений проводников.
Для уменьшения влияния скин-эффекта применяют проводники различного сечения: плоские (в виде лент), трубчатые (полые внутри), наносят на поверхность проводника слой металла с более низким удельным сопротивлением. Например, серебро обладает наибольшей удельной проводимостью среди всех металлов и технологично для нанесения на металлические поверхности, и тонкий его слой, в котором из-за скин-эффекта и протекает бо́льшая часть тока, оказывает заметное снижение (до 10 %) активного сопротивление проводника. Кроме того, слой сульфида, образующийся на поверхности серебра, не проводит ток и не участвует в скин-эффекте, в отличие от слоя окиси-закиси на поверхности меди, обладающего заметной проводимостью, и имеет свойства полупроводника, и вносит дополнительные потери на высоких частотах.
Покрытие серебром также применяется в сверхвысокочастотном оборудовании, использующем колебательные контуры особой формы: объёмные резонаторы и специфические линии передач — волноводы
Кроме того, на таких частотах уделяют внимание снижению шероховатости поверхности с целью уменьшения длины пути протекания тока.. Также применяется и покрытие золотом, у которого слой окислов отсутствует. Напротив, покрытие никелем, оловом или оловянно-свинцовым припоем способно значительно, в несколько раз увеличить сопротивление медных проводников на высоких частотах
Напротив, покрытие никелем, оловом или оловянно-свинцовым припоем способно значительно, в несколько раз увеличить сопротивление медных проводников на высоких частотах.
Также применяется и покрытие золотом, у которого слой окислов отсутствует. Напротив, покрытие никелем, оловом или оловянно-свинцовым припоем способно значительно, в несколько раз увеличить сопротивление медных проводников на высоких частотах.
Так, в ВЧ аппаратуре используют катушки индуктивности намотанные из посеребрённого провода, часто серебрят печатные и проволочные проводники, поверхности экранов и обкладки конденсаторов. В высоковольтных линиях электропередач иногда применяют провод в медной либо алюминиевой оболочке со стальным сердечником[источник?], в мощных генераторах переменного тока обмотка изготавливается из трубок, по которым для охлаждения циркулирует дистиллированная вода.
Также с целью снижения скин-эффекта используют систему из нескольких переплетённых и изолированных проводов — намоточный провод литцендрат.
При передаче больших мощностей на значительные расстояние применяются линии электропередачи постоянного тока — HVDC, Постоянный ток не вызывает скин-эффект.
Поверхностный эффект и его влияние на нагрев
Поверхностный эффект (скин эффект) – это эффект оттеснения переменного электрического тока, протекающего через проводник, к его периферии, вызванный переменным магнитным полем, создаваемым этим током.
Этот эффект имеет высокое значение в области высоких частот и приводит к существенному сокращению эффективной площади сечения проводников. Это приводит к повышенному тепловыделению в проводниках при протекании через них электрического тока и в большинстве случаев требует принятия дополнительных мер для ослабления поверхностного эффекта.
Как это работает
Механизм возникновения поверхностного эффекта стоит рассмотреть на примере проводника круглого сечения, по которому протекает переменный электрический ток. На рисунке представлен проводник в разрезе которого отражены протекающие при скин-эффекте процессы.
| Протекание электрического тока вдоль проводника приводит к возникновению магнитного поля, силовые линии которого изображены на рисунке пунктирной линией. Вектор магнитной индукции B при этом всегда направлен по касательной к силовой линии магнитного поля. Поскольку ток j, протекающий через проводник переменный, вектор индукции магнитного поля также изменяет свою величину и направление с прямого на противоположное с частотой протекающего тока. Изменение вектора магнитной индукции приводит, в соответствии с законом Фарадея, к возникновению напряженности электрического поля E. В проводнике это приводит к возникновению вихревых токов, встречных току j в центральной области проводника и сонаправленных ему на периферии. |
Физически это можно представить как возникновение дополнительной распределенной электродвижущей силы внутри проводника, сонаправленной с направлением протекания тока вблизи периферии проводника и противонаправленной вблизи его оси. Этот эффект приводит к неравномерному распределению протекающего электрического тока в проводнике, при котором большая часть тока протекает в поверхностном слое.
| График распределения плотности тока представлен на рисунке. Эта зависимость имеет экспоненциальный характер и недостаточно удобна при оценке. Поэтому в инженерных расчетах делается следующее упрощение. Глубина, на которой величина плотности тока в 2,7 раза меньше максимальной считается пограничной, и по этой границе формируется условный внешний слой толщиной Δ, по которому равномерно протекает весь ток проводника. Во внутренней же части проводника (обозначена белым) считается, что ток не протекает. Этот внешний слой называется скин-слоем, а его величина определяется свойствами материала проводника и частотой протекающего тока.
Из рисунка видно, что сечение проводника, по которому протекает электрический ток, может быть значительно меньше действительного сечения проводника. Это приводит к избыточному нагреву проводника и потерям электрической мощности на этот нагрев. В условиях передачи высокочастотной электроэнергии по проводнику этот нагрев является крайне нежелательным и требует специальных мер по его снижению. |
Толщина скин-слоя зависит от частоты, удельного электрического сопротивления материала и его магнитной проницаемости. Ярко выраженное изменение толщины скин-слоя происходит при нагреве сплавов на основе железа в сечении заготовки при переходе точки Кюри: толщина скин-слоя при этом увеличивается на порядок и визуально наблюдается утолщение области нагрева.
| Поверхностный эффект имеет огромное значение в индукционном нагреве, поскольку с его помощью можно концентрировать выделение тепловой энергии в поверхности заготовки. Это связано с тем, что нагрев производится вихревыми переменными токами внутри детали, которые протекают также, как и в рассмотренном проводнике — во внешних слоях материала. Это широко используется, например, при поверхностной закалке, когда закаливается только поверхность детали, не изменяя металл в глубине. Для многих задач именно поверхности требуют особой твердости материала. |
Использование высоких частот для объемного нагрева возможно, однако в этом случае, поскольку энергия выделяется в тонком слое, нагрев более глубоких зон будет производится только за счет теплопроводности металла, что увеличивает длительность нагрева и снижает ее равномерность.
Таким образом, для глубинного равномерного нагрева крупных стальных заготовок следует использовать более низкие частоты, в то время как для нагрева небольших деталей, поверхностной закалки или для нагрева немагнитных металлов необходимы установки с более высокими рабочими частотами.
Плотность тока в круглом проводнике
Когда глубина скин-слоя не мала по сравнению с радиусом провода, плотность тока можно описать с помощью функций Бесселя . Плотность тока внутри круглого провода вдали от влияния других полей как функция расстояния от оси определяется выражением:
Плотность тока в круглой проволоке для различной глубины скин-слоя. Числа, показанные на каждой кривой, представляют собой отношение глубины скин-слоя к радиусу провода. Кривая со знаком бесконечности соответствует случаю нулевой частоты (DC). Все кривые нормированы так, чтобы плотность тока на поверхности была одинаковой. Горизонтальная ось — это положение внутри провода, при этом левый и правый крайние точки являются поверхностью провода. По вертикальной оси отложена относительная плотность тока.
- Jрзнак равноkя2πрJ(kр)J1(kр)знак равноJрJ(kр)J(kр){\ displaystyle \ mathbf {J} _ {r} = {\ frac {k \ mathbf {I}} {2 \ pi R}} {\ frac {J_ {0} (kr)} {J_ {1} (kR )}} = \ mathbf {J} _ {R} {\ frac {J_ {0} (kr)} {J_ {0} (kR)}}}
куда
- ω{\ displaystyle \ quad \ omega}= угловая частота тока = 2π × частота
- рзнак равно{\ displaystyle \ quad r =} расстояние от оси провода
- рзнак равно{\ Displaystyle \ quad R =} радиус проволоки
- Jрзнак равно{\ Displaystyle \ quad \ mathbf {J} _ {r} =}вектор плотности тока на расстоянии r от оси провода
- Jрзнак равно{\ Displaystyle \ quad \ mathbf {J} _ {R} =} вектор плотности тока на поверхности провода
- язнак равно{\ Displaystyle \ quad \ mathbf {I} =} полный вектор тока
- Jзнак равно{\ displaystyle \ quad J_ {0} =} Функция Бесселя первого рода порядка 0
- J1знак равно{\ displaystyle \ quad J_ {1} =} Функция Бесселя первого рода, порядок 1
- kзнак равно-jωμρзнак равно1-jδ{\ displaystyle \ quad к = {\ sqrt {\ frac {-j \ omega \ mu} {\ rho}}} = {\ frac {1-j} {\ delta}}}волновое число в проводнике
- δзнак равно2ρωμ{\ displaystyle \ quad \ delta = {\ sqrt {\ frac {2 \ rho} {\ omega \ mu}}}} также называется глубиной кожи.
- ρ{\ Displaystyle \ quad \ rho} = удельное сопротивление проводника
- μр{\ displaystyle \ quad \ mu _ {r}}= относительная магнитная проницаемость проводника
- μ{\ displaystyle \ quad \ mu _ {0}}= проницаемость свободного пространства = 4π x 10 −7 Гн / м
- μ{\ Displaystyle \ quad \ mu} знак равно μр{\ displaystyle \ mu _ {r}}μ{\ displaystyle \ mu _ {0}}
Поскольку является комплексным, функции Бесселя также являются комплексными. Амплитуда и фаза плотности тока меняется с глубиной.
k{\ displaystyle k}
4-вектор плотности тока
Данное обозначение из теории относительности призвано обобщать явление плотности на пространственно-временной континуум, оперирующий четырьмя измерениями. Такой четырехвектор включает в себя трехвекторное выражение токовой плотности (скалярной величины) и имеющей объем плотности электрического заряда. Использование четырехвектора дает возможность формулировать электродинамические уравнения ковариантным образом.
Рассматриваемая величина необходима для описания концентрации и равномерности распределения заряженных микрочастиц по проводниковому материалу, в котором существует та или иная форма электротока. При оперировании с выражениями, содержащими величину, нужно не забывать о ее скалярности.
Учёт эффекта в технике и борьба с ним
Это явление оказывает заметное влияние по мере увеличения частоты сигнала. Следует учитывать скин эффект при проектировании схем с переменными (импульсными) токами. В частности, делают коррекцию расчета катушки фильтра, колебательного контура, трансформатора.
Типовые способы решения обозначенных проблем:
- уменьшение толщины проводника;
- создание полых конструкций;
- образование поверхностного слоя из металла с лучшей проводимостью;
- устранение неровностей;
- плетение из нескольких изолированных жил.
К сведению. Радикальное устранение вредных явлений организуют с помощью передачи электроэнергии постоянным током.
Формула
Плотность переменного тока J в проводнике экспоненциально уменьшается от своего значения на поверхности J S в
соответствии с глубиной d от поверхности следующим образом:
- Jзнак равноJSе-(1+j)dδ{\ Displaystyle J = J _ {\ mathrm {S}} \, e ^ {- {(1 + j) d / \ delta}}}
где называется глубиной скин-слоя . Таким образом, глубина скин-слоя определяется как глубина под поверхностью проводника, на которой плотность тока упала до 1 / е (около 0,37) Дж · с . Мнимая часть показателя степени показывает, что фаза плотности тока задерживается на 1 радиан для каждой глубины проникновения скин-слоя. Одна полная длина волны в проводнике требует 2π глубины скин-слоя, в этот момент плотность тока ослабляется до e −2π (1,87 × 10 -3 , или -54,6 дБ) от его поверхностного значения. Длина волны в проводнике намного короче, чем длина волны в вакууме , или, что то же самое, в проводнике намного меньше, чем скорость света в вакууме. Например, радиоволна с частотой 1 МГц имеет длину волны в вакууме λ около 300 м, тогда как в меди длина волны уменьшается до примерно 0,5 мм с фазовой скоростью только примерно 500 м / с. Вследствие закона Снеллиуса и этой очень крошечной фазовой скорости в проводнике любая волна, попадающая в проводник, даже при скользящем падении, преломляется в основном в направлении, перпендикулярном поверхности проводника.
δ{\ displaystyle \ delta}
Общая формула для определения глубины скин-слоя при отсутствии диэлектрических или магнитных потерь:
- δзнак равно2ρωμ1+(ρωε)2+ρωε{\ displaystyle \ delta = {\ sqrt {{2 \ rho} \ over {\ omega \ mu}}} \; \; {\ sqrt {{\ sqrt {1+ \ left ({\ rho \ omega \ varepsilon}) \ right) ^ {2}}} + \ rho \ omega \ varepsilon}}}
куда
- ρ{\ displaystyle \ rho} = удельное сопротивление проводника
- ω{\ displaystyle \ omega}= угловая частота тока = , где — частота.2πж{\ displaystyle 2 \ pi f}ж{\ displaystyle f}
- μ{\ displaystyle \ mu}= проницаемость проводника,μр{\ displaystyle \ mu _ {r}}μ{\ displaystyle \ mu _ {0}}
- μр{\ displaystyle \ mu _ {r}}= относительная магнитная проницаемость проводника
- μ{\ displaystyle \ mu _ {0}}= проницаемость свободного пространства
- ε{\ displaystyle \ varepsilon}= диэлектрическая проницаемость проводника,εр{\ displaystyle \ varepsilon _ {r}}ε{\ displaystyle \ varepsilon _ {0}}
- εр{\ displaystyle \ varepsilon _ {r}}= относительная диэлектрическая проницаемость проводника
- ε{\ displaystyle \ varepsilon _ {0}}= диэлектрическая проницаемость свободного пространства
На частотах намного ниже количество внутри большого радикала близко к единице, и формула обычно имеет вид:
1ρϵ{\ displaystyle 1 / \ rho \ epsilon}
- δзнак равно2ρωμ{\ displaystyle \ delta = {\ sqrt {{2 \ rho} \ over {\ omega \ mu}}}}.
Эта формула действительна на частотах, далеких от сильных атомных или молекулярных резонансов (где была бы большая мнимая часть), и на частотах, которые намного ниже как плазменной частоты материала (зависящей от плотности свободных электронов в материале), так и обратной величины. среднее время между столкновениями с участием электронов проводимости. В хороших проводниках, таких как металлы, все эти условия обеспечиваются, по крайней мере, до микроволновых частот, что подтверждает справедливость этой формулы. Например, в случае меди это будет верно для частот намного ниже 10 18 Гц.
ϵ{\ displaystyle \ epsilon}
Однако в очень плохих проводниках на достаточно высоких частотах множитель под большим радикалом увеличивается. На частотах, намного превышающих допустимые, можно показать, что глубина скин-слоя вместо того, чтобы продолжать уменьшаться, приближается к асимптотическому значению:
1ρϵ{\ displaystyle 1 / \ rho \ epsilon}
- δ≈2ρεμ{\ displaystyle \ delta \ приблизительно {2 \ rho} {\ sqrt {\ varepsilon \ over \ mu}}}
Это отклонение от обычной формулы применимо только к материалам с довольно низкой проводимостью и на частотах, где длина волны вакуума не намного больше, чем сама толщина скин-слоя. Например, объемный кремний (нелегированный) является плохим проводником и имеет толщину скин-слоя около 40 метров на частоте 100 кГц (λ = 3000 м). Однако, поскольку частота увеличивается до мегагерцового диапазона, его скин-толщина никогда не опускается ниже асимптотического значения 11 метров. Вывод состоит в том, что в плохих твердых проводниках, таких как нелегированный кремний, скин-эффект не нужно учитывать в большинстве практических ситуаций: любой ток равномерно распределяется по поперечному сечению материала независимо от его частоты.
Формула вычисления
Рассматриваемая величина находится в обратной зависимости от размеров сечения (чем больше площадь, тем меньше плотность тока) и временного периода прохождения электрозаряда и в прямой – от величины этого заряда.
Это можно записать так:
j=Δq/ΔtΔS (q тут – элементарно малый заряд, t – бесконечно малый промежуток времени, а S – площадь сечения).
Так как токовая сила выражается как частное заряда и временного промежутка его прохода, формулу можно записать и так:
Формула плотности тока с опорой на параметры перемещающихся зарядов будет выглядеть так:
j=q*n*V (V тут – скорость, а n – концентрация электронных частиц).
Падение напряжения на проводе
Итак, если взять неизменной мощность, то при понижении напряжения ток должен возрастать, согласно формуле:
При этом падение напряжения на проводе (потери в проводах) за счет сопротивления рассчитывается, исходя из закона Ома:
Из этих двух формул видно, что при понижении питающего напряжения потери на проводе возрастают. Поэтому чем ниже питающее напряжение, тем большее сечение провода нужно использовать, чтобы передать ту же мощность.
Для постоянного тока, где используется низкое напряжение, приходится тщательно подходить к вопросу сечения и длины, поскольку именно от этих двух параметров зависит, сколько вольт пропадёт зря.
А какая частота считается высокой?
Как уже было сказано, скин эффект проявляется только на переменном сигнале и только на высоких частотах. До этого я специально обходил числовые значения частоты стороной. Но что же означает высокая частота?
Тут стоит заострить внимание на том, что под «высокими частотами» подразумеваются высокие по меркам электроники, а не человеческого слуха. Бороться с проявлением скин эффекта начинают на частотах выше 1МГц. Там может доходить и до того, что проводники делаются не сплошными, а полыми в виде трубок. Т.к
в центральная часть проводника становится не просто ненужной, но еще и вредной для сигнала
Т.к. в центральная часть проводника становится не просто ненужной, но еще и вредной для сигнала.
Конечно скин эффект проявляется и в слышимой области частот. Не зря же об этом пестрят все Хай-Энд издания. Но вот только хитрые маркетологи не говорит о том, насколько проявляется это влияние.
Поверхностный эффект и его влияние на нагрев
Поверхностный эффект – это эффект оттеснения переменного электрического тока, протекающего через проводник, к его периферии, вызванный переменным магнитным полем, создаваемым этим током.
Как сделать спутниковую антенну
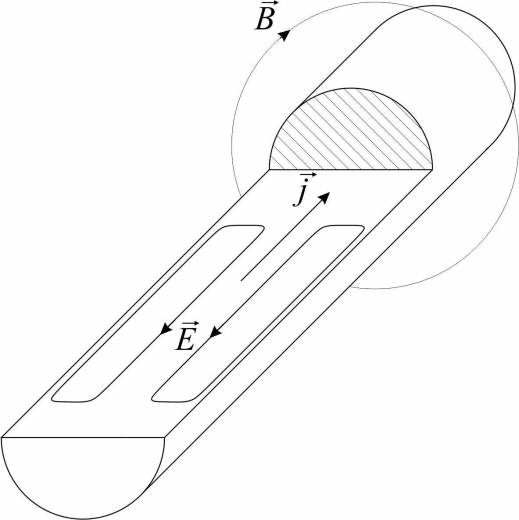
Механизм возникновения поверхностного эффекта стоит рассмотреть на примере проводника круглого сечения, по которому протекает переменный электрический ток.
Протекание электрического тока вдоль проводника приводит к возникновению магнитного поля, силовые линии которого изображены на рисунке. Вектор индукции магнитного поля B при этом всегда направлен по касательной к силовой линии магнитного поля. Поскольку ток j, протекающий через проводник является переменным, вектор индукции магнитного поля также изменяет свой модуль и направление в каждой точке силовой линии в противоположные стороны, а вектор его производной по времени коллинеарен вектору индукции магнитного поля (т.е. векторы могут быть либо сонаправлены либо противонаправлены в каждый момент времени).
Наличие ненулевой первой производной по времени вектора магнитной индукции приводит, в соответствии с законом Фарадея, к возникновению вектора напряженности электрического поля E, ротор которого определяется согласно уравнению Максвелла.
Физически это можно представить как возникновение дополнительной электродвижущей силы, сонаправленной с направлением протекания тока вблизи периферии проводника и противонаправленной вблизи его оси.
Этот эффект приводит к неравномерному распределению протекающего электрического тока в проводнике, при котором большая часть тока протекает в его поверхностном слое.
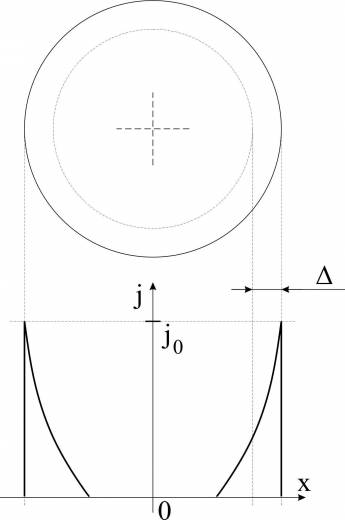
График распределения тока представлен на рисунке. Распределение имеет экспоненциальный характер, поэтому для упрощения расчетов в первом приближении принято считать, что электрический ток протекает равномерно только в поверхностном слое толщиной Δ, называемым скин-слоем, а в остальном сечении проводника — отсутствует. Действительная величина плотности тока на глубине скин-слоя в 2,7 раза меньше плотности тока на поверхности проводника, однако в связи с экспоненциальной характеристикой затухания, на глубине 2Δ плотность тока незначительна, а выделяемая мощность практически равна нулю.
Поверхностный эффект характерен только для протекания переменного тока: при протекании постоянного тока, ток распределяется равномерно по всему сечению проводника. Толщина скин-слоя сильно зависит от частоты, электрического сопротивления материала и его магнитной проницаемости: она уменьшается с увеличением частоты переменного тока и магнитной проницаемости материала и увеличивается с ростом удельного сопротивления согласно соотношению.
Ярко выраженное изменение толщины скин-слоя происходит при нагреве сплавов на основе железа при переходе температуры точки Кюри: толщина скин-слоя при этом увеличивается на порядок, при этом визуально наблюдается увеличение области нагрева.

Поверхностный эффект имеет огромное значение в индукционном нагреве, поскольку с его помощью можно концентрировать выделение тепловой энергии в определенной области заготовки. Это связано с тем, что нагрев производится вихревыми токами внутри детали в области их протекания, а эта область и, следовательно, область нагрева определяется поверхностным эффектом. Это широко используется, например, при поверхностной закалке, когда необходимо закалить только поверхность изделия, не изменяя структуры металла на большей глубине.
Использование частот, при которых толщина скин-слоя намного меньше нагреваемой области возможно, однако в этом случае за счет того, что энергия выделяется в тонком поверхностном слое, нагрев более глубоких зон будет производится слой за слоем за счет теплопроводности металла, что увеличивает длительность нагрева, снижает общий КПД системы, а также не обеспечивает равномерности нагрева.
Таким образом, для глубинного равномерного нагрева крупных стальных заготовок следует использовать более низкие частоты, в то время как для нагрева небольших деталей, для поверхностной закалки или для нагрева немагнитных металлов необходимы ТВЧ преобразователи с частотами на порядок выше.
Для ориентировочного расчета толщины скин-слоя нескольких основных материалов рекомендуется использовать следующие соотношения.
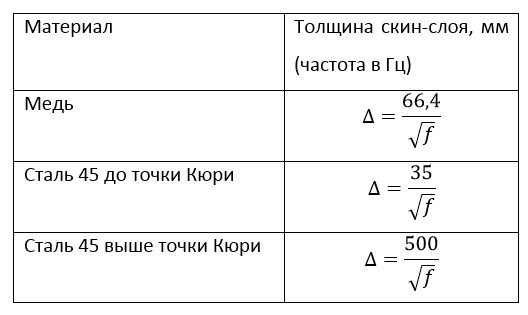
Глубина — скин-слой
| Спектральные зависимости оптических характеристик металла п, — л, о, Л по теории нормального скин-эффекта. I — область соотношений Хагена — Рубенса. II — область релаксации ( средний и ближний ИК-диаиазон. III — область прозрачности ( У Ф — диа-пазон. По оси абсцисс — логарифмический масштаб частоты. |
Глубина скин-слоя здесь составляет — 0 02 — 0 05 мкм, а коэф.
Глубина скин-слоя существенно зависит от проводимости о, частоты эл. На малых частотах б велика, убывает с ростом частоты и для металлов на частотах онтич.
Глубина скин-слоя, как видно из (7.93), пропорциональна корню квадратному из произведения частоты света на электропроводность образца.
Глубина скин-слоя б может резко возрастать, если в плазме возможны процессы трансформации приложенного к плазме перем.
Вычислить классическую глубину скин-слоя и показать, что она значительно меньше средней длины свободного пробега в чистом металле при низких температурах.
Теплота
Вычислить классическую глубину скин-слоя и показать, что она значительно меньше средней длины свободного пробега в чистом металле при низких температурах.
А — глубина скин-слоя; р и Ро — фазовые постоянные в части резонатора, заполненной диэлектриком и воздухом соответственно.
В полупроводниках это приближение представляет наибольший интерес, так как глубина скин-слоя мала из-за сравнительно небольшой проводимости.
Сигнал ЭПР от электронов проводимости прост только для частиц, размер которых мал по сравнению с глубиной скин-слоя. Скин-слой является характеристической величиной, которая показывает глубину проникновения излучения микроволновой мощности.
Эти соотношения справедливы при условии, что глубина проникновения высокочастотного поля в образец на резонансной частоте ( глубина скин-слоя, стр.
Азбель и др. показали, что эффект Оверхаузера позволяет использовать частицы, средний диаметр которых велик либо мал по сравнению с глубиной скин-слоя.
| Возникновение скин-эффекта в проводнике.| Распределение плотности тока в проводнике при возникновении скин-эффекта. |
Если, как обычно, для р в формуле (6.1.1) использовать размерность Ом мм2 / м, а для со — рд / с, то глубина скин-слоя получается в мм.
Такое представление в основном правильно, но необходимо внести две небольшие поправки: на микроволновых частотах квазичастицы, или нормальная компонента жидкости, могут ускоряться, так что возникает некоторое сопротивление; кроме того, реактивная глубина скин-слоя 6i может примерно на 10 % отличаться от значения Я при нулевой частоте. Метод поверхностного импеданса очень подробно обсуждался Вальдра-мом ; в частности, для получения Я из 6t, а также значений поверхностного сопротивления по целой области частот, Вальдрам воспользовался соотношением Крамерса — Кронига.