Формулы расчета резонансной частоты колебательного контура: амплитуда резонанса

Расстройка устройства

Расстройка — это настройка контура на частоту, отличную от резонансной. Последняя наступает в том случае, когда характеристики частот радиодетали и генератора совпадают. В некоторых устройствах этого необходимо избегать. Чтобы получить резонанс, нужно воспользоваться одним из трех методов изменения характеристик:

• частоты генератора;
• индуктивности;
• емкости.

Два последних метода можно делать одновременно для достижения лучшего эффекта. Расстройки классифицируются на три вида: абсолютную, обобщенную и относительную. Первой называется разность между частотами контура и резонанса. Обобщенная вычисляется при помощи отношения реактивного сопротивления к активному. Относительная выражается в виде отношения абсолютной расстройки к резонансной частоте.

Кроме того, расстройка бывает положительной и отрицательной. В первом случае необходимо, чтобы частота генератора была больше частоты контура. Для отрицательной должно соблюдаться другое условие: частота генератора меньше, чем у контура.

В некоторых случаях необходимо убрать резонансную частоту. Выполняется такая операция при помощи изменения необходимых характеристик электроцепи «контур — генератор». Очень часто в контуре применяются конденсаторы с переменной емкостью, позволяющие настраивать его. Настройка конденсатора происходит благодаря изменению расстояния между его обкладками. Этот принцип очень удобен, поскольку для изменения индуктивности катушки необходим сердечник, который будет выкручиваться.

Где применяется колебательный контур?

Самое знакомое нам применение составляющих контура — это электромагниты. Они, в свою очередь, используются в домофонах, электродвигателях, датчиках и во многих других не столь обыденных областях. Другое применение — генератор колебаний. На самом деле это использование контура нам очень знакомо: в этом виде он применяется в микроволновке для создания волн и в мобильной и радиосвязи для передачи информации на расстояние. Всё это происходит благодаря тому, что колебания электромагнитных волн можно закодировать таким образом, что станет возможным передавать информацию на большие расстояния.

Катушка индуктивности сама по себе может использоваться как элемент трасформатора: две катушки с разным числом обмоток могут передавать с помощью электромагнитного поля свой заряд. Но так как характеристики соленоидов различаются, то и показатели тока в двух цепях, к которым подключены эти две индуктивности, будут различаться. Таким образом можно преобразовывать ток с напряжением в 220 вольт в ток с напряжением в 12 вольт.

Свободные колебания

Определение 1

Свободные колебания в электрическом контуре носят название гармонических при условии отсутствия затухания.

Такие колебания происходят по закону:

q(t)=q cos(ωt+φ).

Параметры L и C колебательного контура определяют лишь собственную частоту свободных колебаний:

ω=1LC

Определение 2

«Начальными условиями», определяющими амплитуду q и начальную фазу φ, называют тот способ, при помощи которого систему вывели из равновесия.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Пример 1

Например, для процесса колебаний, который начнется в контуре, изображенном на рисунке 2.2.1, после перевода ключа K в второе положение, q=Cδ, φ=.

Процесс свободных колебаниях провоцирует повторяющееся превращение запасенной в конденсаторе электрической энергии Wэ в магнитную энергию катушки Wм и наоборот. В ситуации, когда потери энергии равны нулю, полная электромагнитная энергия системы не претерпевает изменений:

W=Wэ+Wм=q22C+LJ22=const

Однако любой реально существующий контур, в отличие от идеального, включает в себя некоторое сопротивление R. По этой причине, процесс свободных колебаний в подобном контуре не подчиняется гармоническому закону. Запасенная в контуре энергия с каждым периодом колебаний теряется, превращаясь в джоулево тепло, из-за чего колебания становятся затухающими (рис. 2.2.3).

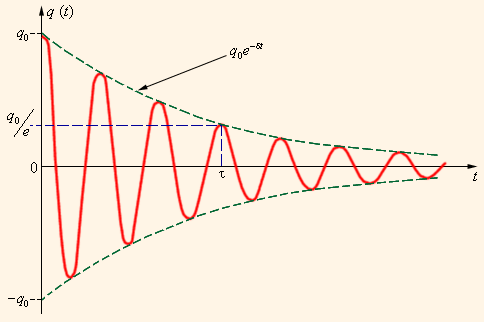
Рисунок 2.2.3. Затухающие колебания в контуре.

Затухающие колебания в электрическом контуре сравнимы с затухающими колебаниями груза на пружине в условиях существующего вязкого трения, при котором сила трения меняет свое значение прямо пропорционально скорости тела: Fтр=–βυ.

В данной формуле сопротивление R электрического контура аналогично коэффициенту β. Уравнение свободных колебаний в контуре при наличии затухания принимает следующий вид:

q··+2δq·+ω2q=

Определение 3

Коэффициентом затухания называется физическая величина δ=R2L.

Следующая функция представляет собой решение приведенного выше дифференциального уравнения:

q(t)=qe-δtcos (ωt+φ),

Также она содержит описывающий затухание колебаний множитель exp (–δt). Скорость затухания зависит от электрического сопротивления R контура.

Определение 4

Интервал времени τ=1δ, в течение которого амплитуда колебаний уменьшается в e≈2,7 раза, называется временем затухания.

Q=πN=πτT,

где N является числом полных колебаний, которые совершает система за время затухания τ.

Определение 5

Любая добротность Q, относящаяся к колебательной системе, которая способна совершать свободные колебания, имеет следующее энергетическое определение: 

Q=2πЗапас энергии в колебательной системеПотеря энергии за 1 период

Добротность Q, принадлежащая RLC-контуру, выражают формулой: 

Q=1RLC

Добротность электрических контуров, которые применяются в радиотехнике, обычно порядка нескольких десятков и даже сотен.

Стоит обратить внимание на то, что собственная частота ω свободных колебаний в контуре с не самой высокой добротностью несколько уступает собственной частоте ω идеального контура с такими же значениями L и C. Однако при Q≥(5÷10) данным различием можно пренебречь

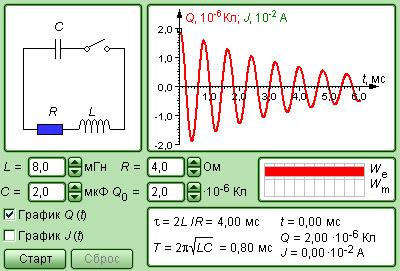
Рисунок 2.2.4. Модель свободных колебаний в RLC-контуре.

Всё ещё сложно?
Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

Как работает контур колебаний

Работа контура колебаний основана на циклическом преобразовании энергии индуктивности в качественный показатель эффективности конденсатора и наоборот. Допустим, что конденсатор полностью заряжен и энергия, запасенная в нем, максимальна. При подключении его к катушке индуктивности, он начинает разряжаться. При этом, через индуктивность начинает протекать ток, вызывающий появление ЭДС самоиндукции, направленную на уменьшение протекающего тока. Это означает, что начинается процесс перезарядки конденсатора. В тот момент, когда энергия прибора становится равной нулю, та же величина для катушки максимальна.

Далее, энергия индуктивности снижается, расходуясь на заряд емкости с противоположной полярностью. После уменьшения показателя коэффициента самоиндукции до нуля, на конденсаторе она опять имеет максимальное значение.

Вам это будет интересно Средства защиты от статического электричества

Процессы в системе

Важно! В идеальном случае, данный процесс способен протекать бесконечно. В реальных устройствах колебание затухает со скоростью, пропорциональной потерям в цепи проводников

Вне зависимости от величины энергии, наличия потерь, частота колебаний постоянна и зависит только от значений параметров коэффициента самоиндукции и емкости. Данная величина называется резонансной. Формула резонанса учитывает значение величины емкости и индуктивности контура колебаний.

Осциллограмма

При воздействии на электрическую цепь с катушкой внешним сигналом с частотой, равной резонансной, амплитуда изменения положения частиц резко возрастает. Резонанс отсутствует при несовпадении частот. Из-за предельных значений электрическую цепь с катушкой индуктивности часто называют резонансной.

Потери в цепи с катушкой индуктивности (потери в диэлектрике конденсатора, сопротивление самого устройства, соединительных проводов) ограничивают величину предельных изменений направления частиц. В следствие этого, введена характеристика электроцепи, именуемая добротностью. Добротность обратно пропорциональна предельной величине потерь.

Зависимость предельной частоты от добротности

Важно! Снижение добротности приводит к тому, что предел изменения направлений наступает не только на основной частоте, но и на некотором приближении к ней, то есть, в некоторой полосе частот, где резонансное значение находится посередине. Чем выше добротность, тем более узкой становится полоса частот

Что такое ёмкость конденсатора?

Ёмкость конденсатора представляет собой отношение заряда конденсатора к напряжению, под которым он находится. Посчитать эту величину можно очень просто с помощью математической формулы:

C = (e0*S)/d, гдеe0 — диэлектрическая проницаемость материала диэлектрика (табличная величина), S — площадь обкладок конденсатора, d — расстояние между пластинами.

Зависимость ёмкости конденсатора от расстояния между обкладками объясняется явлением электростатической индукции: чем меньше расстояние между пластинами, тем сильнее они влияют друг на друга (по закону Кулона), тем больше заряд обкладок и меньше напряжение. А при уменьшении напряжения увеличивается значение ёмкости, так как её также можно описать следующей формулой:

C = q/U, гдеq — заряд в кулонах.

Стоит поговорить о единицах измерения этой величины. Ёмкость измеряется в фарадах. 1 фарад — достаточно большая величина, поэтому существующие конденсаторы (но не ионисторы) имеют ёмкость, измеряемую в пикофарадах (одна триллионная фарада).

Резонанс

Если схема с конденсатором, катушкой и резистором возбуждается напряжением, постоянно меняющимся во времени с определенной частотой, то также изменяются реактивные сопротивления: индуктивное и емкостное. Амплитуда и частота выходного сигнала будет изменяться по сравнению с входным.

Частота вращения: формула

Индуктивное сопротивление прямо пропорционально частоте:

X(L) = 2π x f x L,

а емкостное сопротивление обратно пропорционально этому показателю:

X(C) = 1/(2π x f x C).

Важно! На более низких частотах индуктивное сопротивление незначительное, а емкостное будет высоким и сможет создавать практически разомкнутый контур. На высоких частотах картина обратная

При конкретной комбинации конденсатора и катушки схема становится резонансной, или настроенной, имеющей частоту колебаний, при которой индуктивное сопротивление идентично емкостному. И они компенсируют друг друга.

Следовательно, в цепи остается исключительно активное сопротивление, противостоящее протекающему току. Созданные условия получили наименование резонанса колебательного контура. Фазовый сдвиг между током и напряжением отсутствует.

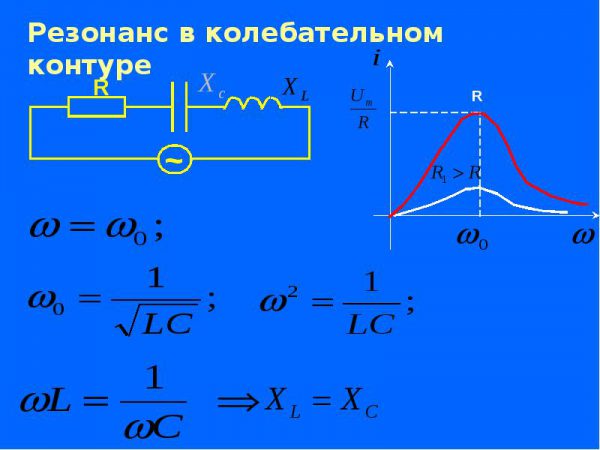
Резонанс LC-цепи

Для расчета резонансной частоты колебательного контура учитывается следующее условие:

X(L) = X(C).

Следовательно, 2π x f x L = 1/(2πx f x C).

Отсюда получается формула резонансной частоты:

f = 1/(2π x √(L x C)).

Расчет резонансной частоты, индуктивности и емкости можно сделать на онлайн калькуляторе, подставив конкретные значения.

Скорость, с которой рассеивается энергия от LC-схемы, должна быть такой же, как энергия, подаваемая на схему. Устойчивые, или незатухающие, колебания производятся электронными схемами генераторов.

LC-цепи используются либо для генерации сигналов на определенной частоте, либо для выделения частотного сигнала из более сложного. Они являются ключевыми компонентами многих электронных устройств, в частности радиооборудования, используемого в генераторах, фильтрах, тюнерах и частотных микшерах.

Колебательный контур

Колебательный контур – это последовательное или параллельное соединение индуктивных и конденсаторных элементов, генерирующих электромагнитные колебания любой заданной частоты. Оба компонента схемы способны хранить энергию.

Когда существует разность потенциалов на конденсаторных пластинах, он сохраняет энергию электрического поля. Аналогично энергия сохраняется в магнитном поле индуктивной катушки.

Работа колебательного контура

Когда первоначально конденсатор подключается к источнику постоянного тока, на нем возникает разность потенциалов. Одна пластина имеет избыток электронов и заряжена отрицательно, другая – недостаток электронов и заряжена положительно.

Что будет, если в цепь включить индуктивную катушку:

1. При замыкании контакта, соединяющего электроцепь, конденсатор начинает разряжаться через катушку индуктивности. Накопленная им энергия электрического поля снижается;
2. Ток, протекающий через катушку L, индуцирует ЭДС, противостоящую потоку электронов. Из-за этого скорость нарастания тока медленная. В катушке создается магнитное поле, которое начинает накапливать свою энергию. После полного разряда конденсатора поток электронов через катушку уменьшается до нуля. Электростатическая энергия, накопленная в конденсаторе, преобразуется в энергию магнитного поля катушки;
3. Когда конденсатор разряжен, магнитное поле начинает постепенно разрушаться, но, согласно закону Ленца, индукционный ток катушки способствует заряду конденсатора с противоположной полярностью. Энергия, связанная с магнитным полем, снова превращается в электростатическую;

Важно! В идеальном случае, когда нет потерь на L и С, конденсатор зарядился бы до первоначального значения с противоположным знаком

1. После того, как уменьшающееся магнитное поле перезарядило конденсатор, он снова начинает разряжаться с потоком тока обратной направленности, а МП опять нарастает.

Последовательность зарядки и разрядки продолжается, то есть процесс преобразования электростатической энергии в магнитную и наоборот периодически повторяется, подобно маятнику, у которого потенциальная энергия циклически превращается в кинетическую и обратно.

Непрерывный процесс зарядки и разрядки приводит к меняющему направление движению электронов или к колебательному току.

Обмен энергией между L и С будет продолжаться бесконечно, если отсутствуют потери. Часть энергии теряется, рассеиваясь в виде тепла на проводах катушки, соединительных проводниках, из-за тока утечки конденсатора, электромагнитного излучения. Поэтому колебания будут затухающими.

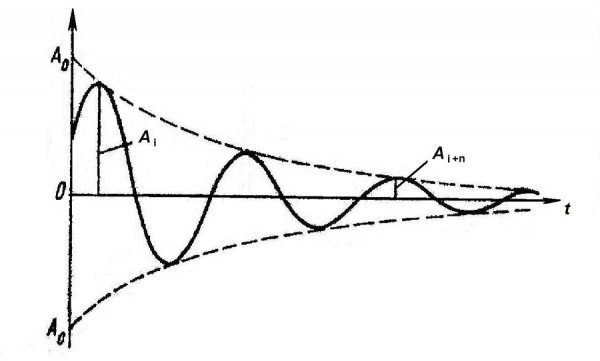
Затухающие колебания

Как связать параметры контура?

Теперь мы вплотную подошли к физике работы колебательного контура. Со временем заряд на обкладках конденсатора изменяется согласно дифференциальному уравнению второго порядка.

Если решить это уравнение, из него следует несколько интересных формул, описывающих процессы, протекающие в контуре. Например, циклическую частоту можно выразить через ёмкость и индуктивность.

Однако наиболее простая формула, которая позволяет вычислить многие неизвестные величины, — формула Томсона (названа в честь английского физика Уильяма Томсона, который вывел её в 1853 году):

T = 2*п*(L*C)1/2.T — период электромагнитных колебаний, L и C — соответственно, индуктивность катушки колебательного контура и ёмкость элементов контура, п — число пи.

Решение во временной области

Законы Кирхгофа

По закону Кирхгофа напряжение V _C на конденсаторе плюс напряжение V _L на катушке индуктивности должно равняться нулю:

VC+VLзнак равно{\ displaystyle V_ {C} + V_ {L} = 0.}

Точно так же по закону Кирхгофа ток через конденсатор равен току через катушку индуктивности:

яCзнак равнояL.{\ displaystyle I_ {C} = I_ {L}.}

Из определяющих соотношений для элементов схемы мы также знаем, что

VL(т)знак равноLdяLdт,яC(т)знак равноCdVCdт.{\ displaystyle {\ begin {align} V_ {L} (t) & = L {\ frac {\ mathrm {d} I_ {L}} {\ mathrm {d} t}}, \\ I_ {C} ( t) & = C {\ frac {\ mathrm {d} V_ {C}} {\ mathrm {d} t}}. \ end {align}}}

Дифференциальное уравнение

Преобразование и подстановка дает дифференциальное уравнение второго порядка

d2dт2я(т)+1LCя(т)знак равно{\ displaystyle {\ frac {\ mathrm {d} ^ {2}} {\ mathrm {d} t ^ {2}}} I (t) + {\ frac {1} {LC}} I (t) = 0.}

Параметр ω , резонансная угловая частота , определяется как

ωзнак равно1LC.{\ displaystyle \ omega _ {0} = {\ frac {1} {\ sqrt {LC}}}.}

Используя это, можно упростить дифференциальное уравнение:

d2dт2я(т)+ω2я(т)знак равно{\ displaystyle {\ frac {\ mathrm {d} ^ {2}} {\ mathrm {d} t ^ {2}}} I (t) + \ omega _ {0} ^ {2} I (t) = 0.}

Связанное преобразование Лапласа IS

s2+ω2знак равно,{\ displaystyle s ^ {2} + \ omega _ {0} ^ {2} = 0,}

таким образом

sзнак равно±jω,{\ displaystyle s = \ pm j \ omega _ {0},}

где j — мнимая единица .

Решение

Таким образом, полное решение дифференциального уравнения есть

я(т)знак равноАе+jωт+Bе-jωт{\ displaystyle I (t) = Ae ^ {+ j \ omega _ {0} t} + Be ^ {- j \ omega _ {0} t}}

и может быть решена для A и B с учетом начальных условий. Поскольку экспонента сложная , решение представляет собой синусоидальный переменный ток . Поскольку электрический ток I является физической величиной, он должен быть действительным. В результате можно показать, что константы A и B должны быть комплексно сопряженными :

Азнак равноB*.{\ displaystyle A = B ^ {*}.}

Теперь позвольте

Азнак равноя2е+jϕ.{\ displaystyle A = {\ frac {I_ {0}} {2}} e ^ {+ j \ phi}.}

Следовательно,

Bзнак равноя2е-jϕ.{\ displaystyle B = {\ frac {I_ {0}} {2}} e ^ {- j \ phi}.}

Далее мы можем использовать формулу Эйлера для получения действительной синусоиды с амплитудой I , угловой частотой ω =1√ LC, и фазовый угол .
ϕ{\ displaystyle \ phi}

Таким образом, полученное решение становится

я(т)знак равнояпотому что⁡(ωт+ϕ),{\ Displaystyle I (T) = I_ {0} \ cos \ left (\ omega _ {0} t + \ phi \ right),}

V(т)знак равноLdяdтзнак равно-ωLягрех⁡(ωт+ϕ).{\ displaystyle V (t) = L {\ frac {\ mathrm {d} I} {\ mathrm {d} t}} = — \ omega _ {0} LI_ {0} \ sin \ left (\ omega _ { 0} t + \ phi \ right).}

Первоначальные условия

Начальные условия, удовлетворяющие этому результату, следующие:

я()знак равнояпотому что⁡ϕ,{\ Displaystyle I (0) = I_ {0} \ cos \ phi,}

V()знак равноLdяdт|тзнак равнознак равно-ωLягрех⁡ϕ.{\ Displaystyle V (0) = L {\ frac {\ mathrm {d} I} {\ mathrm {d} t}} {\ Bigg |} _ {t = 0} = — \ omega _ {0} LI_ { 0} \ sin \ phi.}

Терминология

Двухэлементная LC-цепь, описанная выше, представляет собой простейший тип индукционно-конденсаторной сети (или LC -цепи ). Его также называют LC-цепью второго порядка, чтобы отличить ее от более сложных (более высокого порядка) LC- цепей с большим количеством катушек индуктивности и конденсаторов. Такие LC-сети с более чем двумя реактивными сопротивлениями могут иметь более одной резонансной частоты .

Порядок сети — это порядок рациональной функции, описывающей сеть, в переменной комплексной частоты s . Как правило, порядок равен количеству элементов L и C в схеме и ни в коем случае не может превышать это количество.

Последовательная схема

Последовательная цепь LC

В последовательной конфигурации LC-цепи катушка индуктивности (L) и конденсатор (C) соединены последовательно, как показано здесь. Общее напряжение V на открытых клеммах — это просто сумма напряжения на катушке индуктивности и напряжения на конденсаторе. Ток I на положительном выводе схемы равен току через конденсатор и катушку индуктивности.

Vзнак равноVL+VC,язнак равнояLзнак равнояC.{\ displaystyle {\ begin {align} V & = V_ {L} + V_ {C}, \\ I & = I_ {L} = I_ {C}. \ end {align}}}

Резонанс

Величина X _L индуктивного реактивного сопротивления увеличивается с увеличением частоты, а величина X _C уменьшается с увеличением частоты. На одной конкретной частоте эти два реактивных сопротивления равны по величине, но противоположны по знаку; эта частота называется резонансной частотой f для данной цепи.

Следовательно, при резонансе

ИксLзнак равноИксC,ωLзнак равно1ωC.{\ displaystyle {\ begin {align} X_ {L} & = X_ {C}, \\\ omega L & = {\ frac {1} {\ omega C}}. \ end {выравнивается}}}

Решая относительно ω , имеем

ωзнак равноωзнак равно1LC,{\ displaystyle \ omega = \ omega _ {0} = {\ frac {1} {\ sqrt {LC}}},}

которая определяется как резонансная угловая частота контура. Преобразуя угловую частоту (в радианах в секунду) в частоту (в герцах), мы получаем

жзнак равноω2πзнак равно12πLC.{\ displaystyle f_ {0} = {\ frac {\ omega _ {0}} {2 \ pi}} = {\ frac {1} {2 \ pi {\ sqrt {LC}}}}.}

В последовательной конфигурации X _C и X _L компенсируют друг друга. В реальных, а не идеализированных компонентах току противодействует, в основном, сопротивление обмоток катушки. Таким образом, ток, подаваемый в последовательный резонансный контур, максимален при резонансе.

• В пределе f → f ток максимален. Сопротивление цепи минимальное. В этом состоянии цепь называется приемной цепью.
• Для е < е , X _L «- X _C . Следовательно, цепь емкостная.
• Для е > е , X _L »- X _C . Следовательно, цепь индуктивна.

Импеданс

В последовательной конфигурации резонанс возникает, когда комплексное электрическое сопротивление цепи приближается к нулю.

Сначала рассмотрим импеданс последовательной LC-цепи. Полный импеданс определяется суммой индуктивного и емкостного сопротивлений:

Zзнак равноZL+ZC.{\ displaystyle Z = Z_ {L} + Z_ {C}.}

Записывая индуктивное сопротивление как Z _L = jωL и емкостное сопротивление как Z _C =1jωC и замена дает

Z(ω)знак равноjωL+1jωC.{\ Displaystyle Z (\ omega) = j \ omega L + {\ frac {1} {j \ omega C}}.}

Запись этого выражения под общим знаменателем дает

Z(ω)знак равноj(ω2LC-1ωC).{\ displaystyle Z (\ omega) = j \ left ({\ frac {\ omega ^ {2} LC-1} {\ omega C}} \ right).}

Наконец, определяя собственную угловую частоту как

ωзнак равно1LC,{\ displaystyle \ omega _ {0} = {\ frac {1} {\ sqrt {LC}}},}

импеданс становится

Z(ω)знак равноjL(ω2-ω2ω).{\ displaystyle Z (\ omega) = jL \ left ({\ frac {\ omega ^ {2} — \ omega _ {0} ^ {2}} {\ omega}} \ right).}

Числитель означает, что в пределе ω → ± ω полный импеданс Z будет равен нулю, а в противном случае отличен от нуля. Следовательно, последовательный LC-контур при последовательном включении с нагрузкой будет действовать как полосовой фильтр, имеющий нулевой импеданс на резонансной частоте LC-контура.

Самоиндукция. Энергия магнитного поля

Самоиндукция является важным частным случаем электромагнитной индукции, когда изменяющийся магнитный поток, вызывающий ЭДС индукции, создается током в самом контуре. Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре.

Собственный Φ, пронизывающий контур или катушку с током, пропорционален силе тока I

Коэффициент пропорциональности L в этой формуле называется коэффициентом самоиндукциииндуктивностью катушки. Единица индуктивности в СИ называется генри (Гн). Индуктивность контура или катушки равна или 1 Гн, если при силе постоянного тока 1 А собственный поток равен 1 Вб

В качестве примера рассчитаем индуктивность длинного соленоида, имеющего N витков, площадь сечения S и длину l. Магнитное поле соленоида определяется формулой (см. § 1.17)

где I – ток в соленоиде, n = N / e – число витков на единицу длины соленоида.

Магнитный поток, пронизывающий все N витков соленоида, равен

Следовательно, индуктивность соленоида равна

где V = Sl – объем соленоида, в котором сосредоточено магнитное поле. Полученный результат не учитывает краевых эффектов, поэтому он приближенно справедлив только для достаточно длинных катушек. Если соленоид заполнен веществом с μ, то при заданном токе I индукция магнитного поля возрастает по модулю в μ раз (см. § 1.17); поэтому индуктивность катушки с сердечником также увеличивается в μ раз:

ЭДС самоиндукции, возникающая в катушке с постоянным значением индуктивности, согласно формуле Фарадея равна

ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней.

Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии. Если включить электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, то при размыкании ключа наблюдается кратковременная вспышка лампы (рис. 1.21.1). Ток в цепи возникает под действием ЭДС самоиндукции. Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.

Из закона сохранения энергии следует, что вся энергия, запасенная в катушке, выделится в виде джоулева тепла. Если обозначить через R полное сопротивление цепи, то за время Δt выделится количество теплоты ΔQ = I2RΔt.

Ток в цепи равен

Выражение для ΔQ можно записать в виде

В этом выражении ΔI < 0; ток в цепи постепенно убывает от первоначального значения I до нуля. Полное количество теплоты, выделившейся в цепи, можно получить, выполнив операцию интегрирования в пределах от I до 0. Это дает

Эту формулу можно получить графическим методом, изобразив на графике зависимость магнитного потока Φ(I) от тока I (рис. 1.21.2). Полное количество выделившейся теплоты, равное первоначальному запасу энергии магнитного поля, определяется площадью изображенного на рис. 1.21.2 треугольника.

Таким образом, энергия W_м магнитного поля катушки с индуктивностью L, создаваемого током I, равна

Применим полученное выражение для энергии катушки к длинному соленоиду с магнитным сердечником. Используя приведенные выше формулы для коэффициента самоиндукции L_μ соленоида и для магнитного поля B, создаваемого током I, можно получить:

где V – объем соленоида. Это выражение показывает, что магнитная энергия локализована не в витках катушки, по которым протекает ток, а рассредоточена по всему объему, в котором создано магнитное поле. Физическая величина

равная энергии магнитного поля в единице объема, называется объемной плотностью магнитной энергии. Дж. Максвелл показал, что выражение для объемной плотности магнитной энергии, выведенное здесь для случая длинного соленоида, справедливо для любых магнитных полей.

Похожие записи:

Искусственное и естественное освещение: основные понятия и стадии расчета Понятие и принцип действия защитного заземления Как правильно штробить стены под электропроводку Простой ремонт микроволновки своими руками: 5 решений основных проблем Способы крепления настольной лампы Настройка icprog под windows 10