Сила лоренца правило левой руки

История

Современное понятие электрических и магнитных полей сначала возникло в теориях Майкла Фарадея, особенно его идея линий силы, позже чтобы быть данным полное математическое описание лорда Келвина и Джеймса Клерка Максвелла. С современной точки зрения возможно определить в формулировке Максвелла 1865 года его уравнений поля форму уравнения силы Лоренца относительно электрических токов, однако, во время Максвелла, не было очевидно, как его уравнения имели отношение к силам при перемещении заряженных объектов. Дж. Дж. Томсон был первым, чтобы попытаться получить из уравнений поля Максвелла электромагнитные силы на перемещении заряженный объект с точки зрения свойств объекта и внешних областей. Заинтересованный определением электромагнитного поведения заряженных частиц в лучах катода, Thomson опубликовал работу в 1881 в чем, он дал силу на частицах из-за внешнего магнитного поля как

Thomson получил правильную каноническую форму формулы, но, из-за некоторых просчетов и неполного описания тока смещения, включал неправильный коэффициент пропорциональности половины перед формулой. Именно Оливер Хивизид, изобрел современное векторное примечание и применил их к уравнениям поля Максвелла, которые в 1885 и 1889 фиксировали ошибки происхождения Thomson и достигли правильной формы магнитной силы на перемещении заряженный объект. Наконец, в 1892, Хендрик Лоренц получил современную форму формулы для электромагнитной силы, которая включает вклады в полную силу и от электрического и от магнитных полей. Лоренц начал, оставив описания Maxwellian эфира и проводимости. Вместо этого Лоренц сделал различие между вопросом и luminiferous эфиром и стремился применить уравнения Максвелла в микроскопическом масштабе. Используя версию Хивизида уравнений Максвелла для постоянного эфира и применения лагранжевой механики (см. ниже), Лоренц достиг правильного, и заполните форму закона о силе, который теперь носит его имя.

Усиление и движущая ЭДС

Когда провод, несущий электрический ток, помещается в магнитное поле, каждый из движущихся зарядов, которые составляют ток, испытывает силу Лоренца. Вместе они могут создавать макроскопическую силу Лапласа. Исходя из этого, получается формула F = Iℓ x B, где ℓ — вектор, величина которого и есть длина проволоки. Его направление выровнено с движением обычного тока.

Если проволока не прямая, а изогнутая, расчёт происходит путём применения этого уравнения к каждому бесконечно малому сегменту проводника d ℓ. Затем нужно сложить всё посредством интегрирования. Формально чистая сила равна F = I ∫ dℓ x B. Кроме того, обычно возникает крутящий момент и другие эффекты, если провод не является абсолютно жёстким.

Компонент (qv x B) отвечает за движущую электродвижущей силы (ЭДС). Это явление, лежащее в основе многих электрических генераторов, исключая те, в которых движутся только магниты, а не проводники. В таких случаях ЭДС обусловлена (q E). Такое явление описано уравнением Максвелла — Фарадея.

Обе ЭДС, несмотря на их различное происхождение, описаны законом индукции Фарадея. Теория относительности Эйнштейна была частично мотивирована желанием лучше понять эту связь между двумя эффектами. На самом деле, электрические и магнитные поля являются разными гранями одного и того же электромагнитного поля. Поэтому при переходе от одной инерциальной системы отсчёта в другую (соленоидальное векторное поле) часть E может измениться в целом или частично стать B или наоборот.

Сила тяжести: формула

Как вычислить силу тяжести, направленную на определенное тело? Какие другие величины необходимо знать для того? Формула расчета силы тяжести довольно проста, ее изучают в 7-м классе общеобразовательной школы, в начале курса физики. Чтобы ее не просто выучить, но и понять, следует исходить из того, что сила тяжести, неизменно действующая на тело, прямо пропорциональна его количественной величине (массе).

Единица силы тяжести названа по имени великого ученого— Ньютон.

Сила тяжести (гравитация) всегда направлена строго вниз, к центру земного ядра, благодаря ее воздействию все тела равноускоренно падают вниз. Явления тяготения в повседневной жизни мы наблюдаем повсеместно и постоянно:

предметы, случайно или специально выпущенные из рук, обязательно падают вниз на Землю (или на любую препятствующую свободному падению поверхность);
запущенный в космос спутник не улетает от нашей планеты на неопределенное расстояние перпендикулярно вверх, а остается вращаться на орбите;
все реки текут с гор и не могут быть обращены вспять;
бывает, человек падает и травмируется;
на все поверхности садятся мельчайшие пылинки;
воздух сосредоточен у поверхности земли;
тяжело носить сумки;
из облаков и туч капает дождь, падает снег, град.

Наряду с понятием «сила тяжести» используется термин «вес тела». Если тело расположить на ровной горизонтальной поверхности, то его вес и сила тяжести численно равны, таким образом, эти два понятия часто подменяют, что совсем не правильно.

Определение[править | править код]

Если вещество состоит из частиц одного сорта, то формула имеет вид:

n2−1n2+2=4π3Nα,{\displaystyle {\frac {n^{2}-1}{n^{2}+2}}={\frac {4\pi }{3}}N\alpha ,}

где n{\displaystyle n} — показатель преломления, N{\displaystyle N} — количество частиц в единице объёма, а α{\displaystyle \alpha } — их поляризуемость.

Уточним, что под поляризуемостью частицы здесь понимается коэффициент α{\displaystyle \alpha }, связывающий напряжённость электрического поля E{\displaystyle {\boldsymbol {E}}}, действующего на частицу, с дипольным моментом p{\displaystyle {\boldsymbol {p}}}, образующимся у частицы под действием этого поля:

p=αE.{\displaystyle {\boldsymbol {p}}=\alpha {\boldsymbol {E}}.}

Здесь и далее жирным шрифтом выделяются векторные величины.

Формулу записывают также в виде:

n2−1n2+2⋅Mρ=4π3NAα,{\displaystyle {\frac {n^{2}-1}{n^{2}+2}}\cdot {\frac {M}{\rho }}={\frac {4\pi }{3}}N_{\mathrm {A} }\alpha ,}

где M{\displaystyle M} — молекулярная масса вещества, ρ{\displaystyle \rho } — его плотность, а NA{\displaystyle N_{\mathrm {A} }} — постоянная Авогадро. При этом величину 4π3NAα{\displaystyle {\frac {4\pi }{3}}N_{\mathrm {A} }\alpha } называют молекулярной рефракцией.

Если вещество состоит из частиц нескольких сортов с поляризуемостями αi{\displaystyle \alpha _{i}} и объёмными концентрациями Ni{\displaystyle N_{i}}, то формула принимает вид:

n2−1n2+2=4π3N1α1+N2α2+⋯+Nnαn.{\displaystyle {\frac {n^{2}-1}{n^{2}+2}}={\frac {4\pi }{3}}\left.}

Вывод формулы основан на рассмотрении микроскопического поля и его взаимодействия с атомами, молекулами и ионами вещества. При выводе предполагается, что среда является изотропной, а составляющие её частицы собственным дипольным моментом не обладают.

Действие магнитного поля на движущийся заряд. Сила Лоренца

Подробности: Просмотров: 903

«Физика — 11 класс»

Магнитное поле действует с силой на движущиеся заряженные частицы, в то числе и на проводники с током.
Какова же сила, действующая на одну частицу?

1.
Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца в честь великого голландского физика X. Лоренца, создавшего электронную теорию строения вещества.
Силу Лоренца можно найти с помощью закона Ампера.

Модуль силы Лоренца равен отношению модуля силы F, действующей на участок проводника длиной Δl, к числу N заряженных частиц, упорядоченно движущихся в этом участке проводника:

Так как сила (сила Ампера), действующая на участок проводника со стороны магнитного поля
равна F = | I | BΔl sin α,
а сила тока в проводнике равна I = qnvS
где
q — заряд частиц
n — концентрация частиц (т.е. число зарядов в единице объема)
v — скорость движения частиц
S — поперечное сечение проводника.
тогда получаем:
На каждый движущийся заряд со стороны магнитного поля действует сила Лоренца, равная:

где α — угол между вектором скорости и вектором магнитной индукции.

Сила Лоренца перпендикулярна векторам и .

2.Направление силы Лоренца

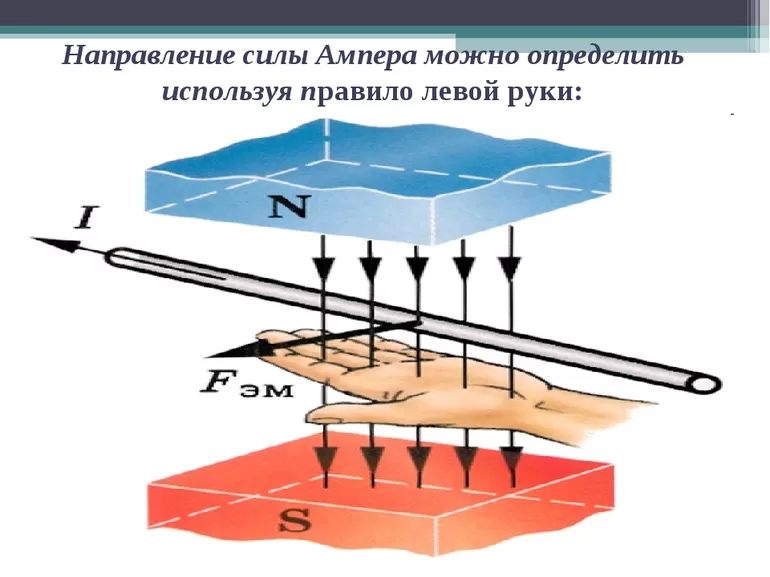
Направление силы Лоренца определяется с помощью того же правила левой руки, что и направление силы Ампера:

Если левую руку расположить так, чтобы составляющая магнитной индукции, перпендикулярная скорости заряда, входила в ладонь, а четыре вытянутых пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90° большой палец укажет направление действующей на заряд силы Лоренца F_л.

3.
Если в пространстве, где движется заряженная частица, существует одновременно и электрическое поле, и магнитное поле, то суммарная сила, действующая на заряд, равна:
= _эл + _л
где сила, с которой электрическое поле действует на заряд q, равна F_эл = q.

4.Cила Лоренца не совершает работы, т.к. она перпендикулярна вектору скорости частицы.
Значит сила Лоренца не меняет кинетическую энергию частицы и, следовательно, модуль ее скорости.
Под действием силы Лоренца меняется лишь направление скорости частицы.

5.Движение заряженной частицы в однородном магнитном поле

однородное

Сила Лоренца зависит от модулей векторов скорости частицы и индукции магнитного поля.
Магнитное поле не меняет модуль скорости движущейся частицы, значит остается неизменным и модуль силы Лоренца.
Сила Лоренца перпендикулярна скорости и, следовательно, определяет центростремительное ускорение частицы.
Неизменность по модулю центростремительного ускорения частицы, движущейся с постоянной по модулю скоростью, означает, чтоВ однородном магнитном поле заряженная частица равномерно движется по окружности радиусом r.

Согласно второму закону Ньютона

Тогда радиус окружности, по которой движется частица, равен:

Время, за которое частица делает полный оборот (период обращения), равно:

6.Использование действия магнитного поля на движущийся заряд.

Действие магнитного поля на движущийся заряд используют в телевизионных трубках-кинескопах, в которых летящие к экрану электроны отклоняются с помощью магнитного поля, создаваемого особыми катушками.

Сила Лоренца используется в циклотроне — ускорителе заряженных частиц для получения частиц с большими энергиями.

На действии магнитного поля основано также и устройство масс-спектрографов, позволяющих точно определять массы частиц..

Следующая страница «Магнитные свойства вещества»

Назад в раздел «Физика — 11 класс, учебник Мякишев, Буховцев, Чаругин»

Магнитное поле. Физика, учебник для 11 класса — Класс!ная физика

Магнитное поле и взаимодействие токов —
Магнитная индукция. Линии магнитной индукции —
Модуль вектора магнитной индукции. Сила Ампера —
Электроизмерительные приборы. Громкоговоритель —
Действие магнитного поля на движущийся заряд. Сила Лоренца —
Магнитные свойства вещества —
Примеры решения задач —
Краткие итоги главы

Примеры из жизни

Насколько вы сильны?

Рассмотрим простейший пример. Ваш ребёнок сел на санки и просит вас его покатать. С какой силой вам нужно тянуть эти санки, чтобы ребёнок остался доволен быстрой ездой ? Пока санки с ребёнком остаются в состоянии покоя, все силы, действующие на них, уравновешены. Состояние покоя — это частный случай инерции. Здесь на санки действуют две силы: тяжести Fт = m•g, направленная вертикально вниз, и нормального давления N, направленная вертикально вверх. Поскольку санки не движутся, то N – m•g = 0. Тогда из этого равенства следует, что N = m•g.

Когда вы решили покатать своего ребёнка, вы прикладываете силу тяги (Fтяги) к санкам с ребёнком. Когда вы начинаете тянуть санки, возникает сопротивление движению, вызванное силой трения (Fтр.), направленной в противоположную сторону. Это так называемая сила трения покоя. Когда тело не движется, она равна нулю. Стоит потянуть за санки — и появляется сила трения покоя, которая меняется от нуля до некоторого максимального значения (Fтр. max). Как только Fтяги превысит Fтр.max, санки с ребёнком придут в движение.

Чтобы найти Fтяги, применим второй закон Ньютона: Fтяги – Fтр.max = m•a, где a – ускорение, с которым вы тянете санки, m – масса санок с ребёнком. Допустим, вы разогнали санки до определённой скорости, которая не изменяется. Тогда a = 0 и вышеприведённое уравнение запишется в виде: Fтяги – Fтр. max = 0, или Fтяги = Fтр.max. Есть известный закон из физики, который устанавливает определённую зависимость для Fтр.max и N. Эта зависимость имеет вид: Fтр.max = fmax • N, где fmax – максимальный коэффициент трения покоя.

Если в эту формулу подставить выражение для N, то мы получим Fтр.max = fmax•m•g. Тогда формула искомой силы тяги примет вид: Fтяги = fmax•m•g = fск•m•g, где fск = fmax – коэффициент трения скольжения, g – ускорение свободного падения. Допустим, fск = 0,7, m = 30 кг, g = 9,81 м/с², тогда Fтяги = 0,7 • 30 кг • 9,81 м/с² = 206,01 Н (Ньютона).

Определение и формула

Хендрик Лоренц доказал, что электромагнитная индукция взаимодействует с заряженными частицами. Эти взаимодействия приводят к возникновению силы Лоренца. Рассматриваемая сила возникает под действием магнитной индукции. Она перпендикулярна вектору скорости движущейся частицы (см. рис. 1). Необходимым условием возникновения этой силы является движение электрического заряда.

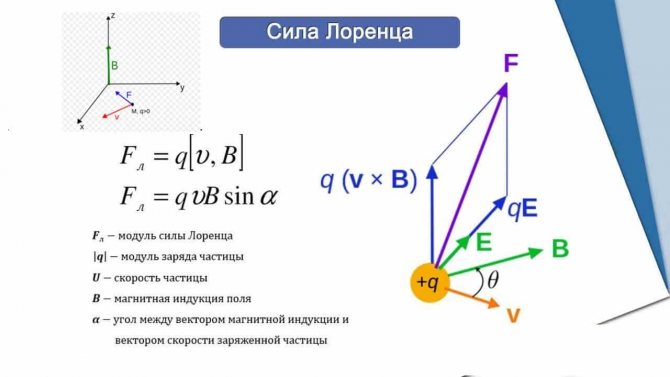
Рис. 1. Выводы Лоренца

Вектор магнитной индукции сориентирован вдоль оси Z, перпендикулярной плоскости XOY, а значит, в выбранной системе координат он перпендикулярен к векторам силы и скорости.

По закону Ампера:

Учитывая, что

(здесь j – плотность тока, q – единичный заряд, n – количество зарядов на бесконечно малую единицу длины проводника, S – сечение проводника, символом v обозначен модуль скорости движущейся частицы), запишем формулу Ампера в виде:

Так, как nSdl – общее число зарядов в объёме проводника, то для нахождения силы, действующей на точечный заряд, разделим выражение на количество частиц:

Модуль F вычисляется по формуле:

Из формулы следует:

Сила Лоренца приобретает максимальное значение, если угол α прямой.
Если точечный заряд, например, электрон, попадает в среду однородного магнитного поля, обладая некой начальной скоростью, перпендикулярной к линиям электромагнитной индукции, тогда вектор F будет перпендикулярен к вектору скорости. На точечный заряд будет действовать центробежная сила, которая заставит его вращаться по кругу. При этом работа равняется нулю (см. рис.2).
Если угол между вектором индукции и скоростью частицы не равняется 90º, тогда заряд будет двигаться по спирали. Направление вращения зависит от полярности заряда (рис. 3).

Рис. 2. Заряженная частица между полюсами магнитов

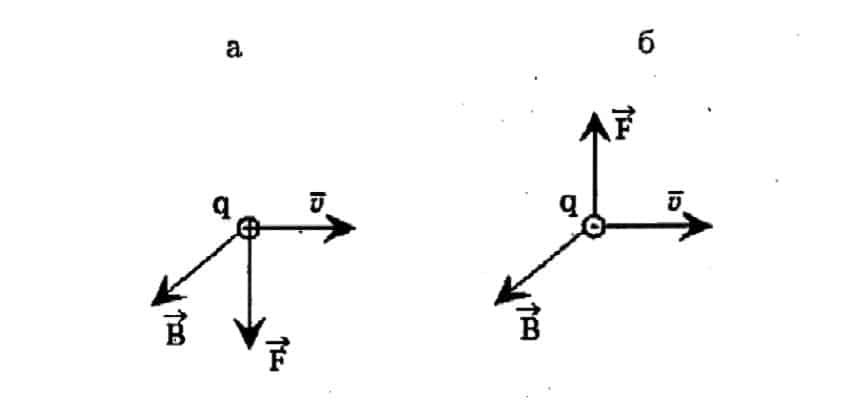
Рис. 3. Ориентация вектора в зависимости от полярности заряда Из рисунка 3 видно, что вектор F направлен в противоположную сторону, если знак заряда меняется на противоположный (при условии, что направления остальных векторов остаются неизменными).

Траекторию движения частицы правильно называть винтовой линией. Радиус этой винтовой линии (циклотронный радиус) определяется перпендикулярной к полю составной начальной скорости частицы. Шаг винтовой линии, вдоль которой перемещается частица, определяется составной начальной скорости заряда, вошедшего в однородное магнитное поле. Эта составная направлена параллельно к электромагнитным линиям.

В чём измеряется?

Размерность силы Лоренца в международной системе СИ – ньютон (Н). Разумеется, модуль силы Лоренца настолько крохотная величина, по сравнению с ньютоном, что её записывают в виде К×10-n Н, где 0<�К<1, а n – порядок числа 10.

Когда возникает?

Магнитные поля не реагируют на неподвижный электрический заряд, так же как не действует сила Ампера на обесточенный проводник.

Для возникновения силы Лоренца необходимо выполнить три условия:

У частицы должен быть отрицательный или положительный заряд.
Заряженная частица должна находиться в магнитном поле.
Частица должна быть в движении, то есть вектор v ≠ 0.

Если хотя бы одно из условий не выполняется, сила Лоренца не возникает.

Урок физики в 9 классе по теме : » Решение задач по теме : «Сила Ампера. Сила Лоренца»»

Тема урока:

«Решение задач по теме «Сила Ампера. Сила Лоренца».

Место урока в системе уроков по теме:

На предыдущем уроке обучающиеся получили знания о векторе магнитной индукции, силе Ампера, силе Лоренца. Данный урок позволяет отработать навыки решения задач по формуле силы Ампера и силы Лоренца .

Цель урока:

показать теоретическую значимость закона Ампера при решении задач, научить применять полученные знания при решении задач.

Задачи урока:

Дидактическая
– создавать условия для усвоения нового учебного материала через проблемно-деятельностный подход.
Образовательная
– рассмотреть применение закона Ампера в ходе решения различных задач.
Развивающая
– развивать логическое мышление обучающихся при решении задач на расчёт силы Амперы и силы Лоренца.
Воспитательная
– прививать культуру умственной деятельности.

Планируемые результаты.

Обучающиеся должны:

овладеть алгоритмом решения задач по данной теме.
уметь решать задачи с применением закона Ампера, формулы для нахождения силы Лоренца .

Техническое обеспечение урока:

Компьютер, проектор, экран.

Дополнительное методическое и дидактическое обеспечение урока:

Презентация к уроку.
Карточки с задачами.

Мобилизующее начало урока («исходная мотивация»). Позитивный настрой на урок.

“Умение решать задачи — это практическое

искусство, подобное плаванию или катанию

на лыжах, или игре на фортепиано: научиться

этому можно, лишь подражая избранным

образцам и постоянно тренируясь”

Д. Пойа

В данной теме рассмотрим основные типы задач, а также попытаемся выделить общую методику их решений. В представленной теме можно выделить три типа задач:

1) на расчет полей (вычисление магнитной индукции, в какой либо точке магнитного поля);

2) о силовом действии магнитного поля на проводники или контур с током;

3) о силовом действии магнитного поля на движущиеся в нем заряженные частицы.

1.Фронтальный опрос:

1.Как называют физ. Величину характеризующую магнитное поле?

2. Какой буквой обозначают?

3. В каких единицах измеряют?

4. Что означает 1 Тл?

5.Какую силу называют силой Ампера? Запишите на доске формулу для расчёта Силы Ампера.

6. Как определяется направление силы Ампера? Сформулируйте правило левой руки.

7.Чему равен модуль вектора магнитной индукции?

8. Какую силу называют силой Лоренца? Запишите на доске формулу для расчёта Силы Лоренца

9. Как определяется направление силы Лоренца? Сформулируйте правило левой руки.

2. Решение задач :

Задача 1 Определить силу, с которой однородное магнитное поле действует на проводник длиной 20 см, если сила тока в нем 300 мА, расположенный под углом 45 градусов к вектору магнитной индукции. Магнитная индукция составляет 0,5 Тл.

Задача 2 Проводник с током 5 А находится в магнитном поле с индукцией 10 Тл. Определить длину проводника, если магнитное поле действует на него с силой 20Н и перпендикулярно проводнику.

Задача 3 Определить силу тока в проводнике длиной 20 см, расположенному перпендикулярно силовым линиям магнитного поля с индукцией 0,06 Тл, если на него со стороны магнитного поля действует сила 0,48 Н.

Задача 4 Проводник длиной 20см с силой тока 50 А находится в однородном магнитном поле с индукцией 40 мТл. Какую работу совершит источник тока, если проводник переместится на 10 см перпендикулярно вектору магнитной индукции (вектор магнитной индукции перпендикулярен направлению тока в проводнике).

Задача 5 Определить силу, действующую на заряд 0,005 Кл, движущийся в магнитном поле с индукцией 0,3 Тл со скоростью 200 м/с под углом 45o к вектору магнитной индукции.

Задача 6 Какова скорость заряженного тела, перемещающегося в магнитном поле с индукцией 2 Тл, если на него со стороны магнитного поля действует сила 32 Н. Скорость и магнитное поле взаимно перпендикулярны. Заряд тела равен 0,5 мКл.

3.Самостоятельная работа по карточкам

4. Рефлексия

5. Д.з.

https://youtube.com/watch?v=eMa11WYguzk

https://youtube.com/watch?v=7IUpOAsKKvI

https://youtube.com/watch?v=mmAB-_2VYPk

Теория Лоренца

Хендрик Антон Лоренц

В 1892 г. голландский физик-теоретик Хендрик Антон Ло́ренц опубликовал работу «Электромагнитная теория Максвелла и её применение к движущимся телам», в которой объединил теорию поля и созданную им теорию электронного строения вещества. Лоренц предположил, что все молекулы вещества состоят из частиц, имеющих электрический заряд. Величина этих зарядов одинакова. Но одни из них заряжены отрицательно, другие положительно. Все эти элементарные заряды создают микроскопические электромагнитные поля, которые описываются уравнениями Максвелла.

Конечно, теория Лоренца имела недостатки и отличалась от современной электронной теории. Но в этой работе учёный вывел формулу силы, действующей на электрический заряд со стороны электромагнитного поля. Эту силу впоследствии назвали силой Лоренца.

Но что же такое электрический ток? Это направленное движение электрических зарядов. И если на каждую заряженную частицу действует сила Лоренца, то на отрезок проводника с током в электромагнитном поле должна действовать сила, величина которой равна сумме всех сил Лоренца, действующих на заряды, образующие электрический ток в проводнике.

И такая сила была открыта задолго до Лоренца. Ещё не зная о существовании силы, действующей на отдельный электрический заряд, французский физик Мари Андре Ампер в 1820 г. описал силу, действующую со стороны электромагнитного поля на проводник с током. Её назвали силой Ампера.

Применение силы Лоренца в технике

Кинескоп

Кинескоп, стоявший до недавнего времени, когда на смену ему пришел LCD-экран (плоский), в каждом телевизоре, не смог бы работать, не будь силы Лоренца. Для формирования на экране телевизионного растра из узкого потока электронов служат отклоняющие катушки, в которых создается линейно изменяющееся магнитное поле. Строчные катушки перемещают электронный луч слева направо и возвращают обратно, кадровые отвечают за вертикальное перемещение, двигая бегающий по горизонтали луч сверху вниз. Такой же принцип используется в осциллографах – приборах, служащих для изучения переменного электрического напряжения.

Watch this video on YouTube

Масс-спектрограф

Масс-спектрограф – прибор, использующий зависимость радиуса вращения заряженной частицы от ее удельного заряда. Принцип его работы следующий:

Источник заряженных частиц, которые набирают скорость с помощью созданного искусственно электрического поля, с целью исключения влияния молекул воздуха помещается в вакуумную камеру. Частицы вылетают из источника и, пройдя по дуге окружности, ударяются в фотопластинку, оставляя на ней следы. В зависимости от удельного заряда меняется радиус траектории и, значит, точка удара. Этот радиус легко измерить, а зная его, можно вычислить массу частицы. С помощью масс-спектрографа, например, изучался состав лунного грунта.

Циклотрон

Независимость периода, а значит, и частоты вращения заряженной частицы от её скорости в присутствии магнитного поля используется в приборе, называемом циклотроном и предназначенном для разгона частиц до высоких скоростей. Циклотрон – это два полых металлических полуцилиндров – дуанта (по форме каждый из них напоминает латинскую букву D), помещенных прямыми сторонами навстречу друг другу на небольшом расстоянии.

Дуанты помещаются в постоянное однородное магнитное поле, а между ними создается переменное электрическое поле, частота которого равна частоте вращения частицы, определяемой напряженностью магнитного поля и удельным зарядом. Попадая дважды за период вращения (при переходе из одного дуанта в другой) под воздействие электрического поля, частица каждый раз ускоряется, увеличивая при этом радиус траектории, и в определенный момент, набрав нужную скорость, вылетает из прибора через отверстие. Таким способом можно разогнать протон до энергии в 20 МэВ (мегаэлектронвольт).

Магнетрон

Устройство, называемое магнетроном, который установлен в каждой микроволновой печи, – еще один представитель приборов, использующих силу Лоренца. Магнетрон служит для создания мощного СВЧ-поля, которое разогревает внутренний объем печи, куда помещается пища. Магниты, входящие в его состав, корректируют траекторию движения электронов внутри прибора.

Магнитное поле Земли

А в природе сила Лоренца играет крайне важную для человечества роль. Её наличие позволяет магнитному полю Земли защитить людей от смертоносного ионизирующего излучения космоса. Поле не дает возможности заряженным частицам бомбардировать поверхность планеты, заставляя их менять направление движения.

Закон Кулона, определение и формула — электрические точечные заряды и их взаимодействие

Определение направления вектора магнитной индукции с помощью правила буравчика и правила правой руки

Что такое ЭДС индукции и когда возникает?

История открытия электричества

Как перевести амперы в ватты и обратно?

Как подключить однофазный электродвигатель — схема с конденсатором

Формула силы трения

Сила трения высчитывается путем произведения реакции опоры N и коэффициента трения k. Формула силы трения будет иметь следующий вид:

Fтр = k * N.

В некоторых формулах коэффициент трения k обозначается символом µ.

Написанные выше расчеты справедливы в самом простом случае, когда тело лежит на строго горизонтальной поверхности.

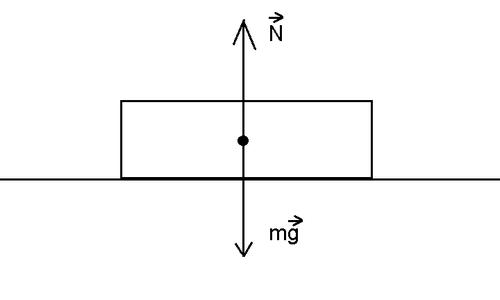
Если же движение происходит по наклонной плоскости, то расчеты силы трения несколько усложняются. На тело, как и раньше, действует сила гравитации и реакция опоры поверхности, но не в одном направлении.

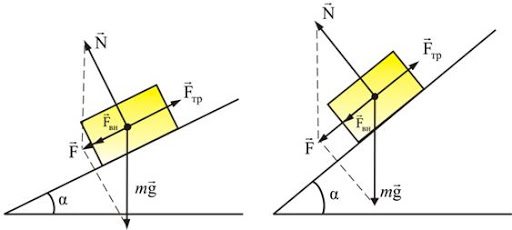
Таким образом, формула силы трения для тела, которое движется по наклонной поверхности, будет иметь следующий вид:

Fтр = k * m * g * cosα.

Где k – коэффициент трения, m – масса тела, g гравитационная постоянная (помним, что она равна 9,8 м/с2), cosα – отношение катета, прилежащего к углу, к гипотенузе треугольника (косинус).

При определении силы трения на наклонных поверхностях ярко проявляется связь между физикой и геометрией.

Магнитное поле

В случае, когда скорость частицы υ→ имеет составляющую υ∥→ вдоль направления магнитного поля, подобная частица в однородном магнитном поле будет совершать спиралевидное движение. Радиус такой спирали R зависит от модуля перпендикулярной магнитному полю составляющей υ┴ вектор υ→, а шаг спирали p – от модуля продольной составляющей υ∥ (рис. 1.18.5).

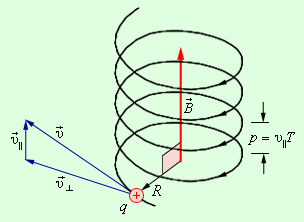
Рисунок 1.18.5. Движение заряженной частицы по спирали в однородном магнитном поле.

Исходя из этого, можно сказать, что траектория заряженной частицы в каком-то смысле «навивается» на линии магнитной индукции. Данное явление используется в технике для магнитной термоизоляции высокотемпературной плазмы — полностью ионизированного газа при температуре порядка 106 K. При изучении управляемых термоядерных реакций вещество в подобном состоянии получают в установках типа «Токамак». Плазма не должна касаться стенок камеры. Термоизоляция достигается путем создания магнитного поля специальной конфигурации. На рисунке 1.18.6 в качестве примера проиллюстрирована траектория движения несущей заряд частицы в магнитной «бутылке» (или ловушке).

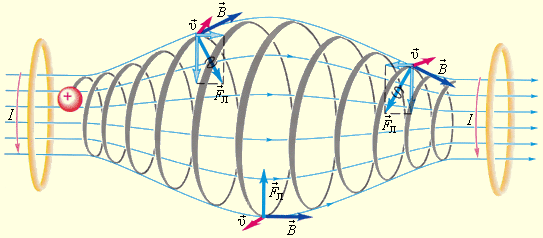
Рисунок 1.18.6. Магнитная «бутылка». Заряженные частицы не выходят за ее пределы. Необходимое магнитное поле может быть создано с помощью двух круглых катушек с током.

Такое же явление происходит в магнитном поле Земли, которое защищает все живое от потока несущих заряд частиц из космического пространства.

Определение 7

Быстрые заряженные частицы из космоса, по большей степени от Солнца, «перехватываются» магнитным полем Земли, вследствие чего образуются радиационные пояса (рис. 1.18.7), в которых частицы, будто в магнитных ловушках, перемещаются туда и обратно по спиралеобразным траекториям между северным и южным магнитными полюсами за доли секунды.

Исключением являются полярные области, в которых часть частиц прорывается в верхние слои атмосферы, что может приводить к возникновению таких явлений, как «полярные сияния». Радиационные пояса Земли простираются от расстояний около 500 км до десятков радиусов нашей планеты. Стоит вспомнить, что южный магнитный полюс Земли находится поблизости с северным географическим полюсом на северо-западе Гренландии. Природа земного магнетизма до сих пор не изучена.

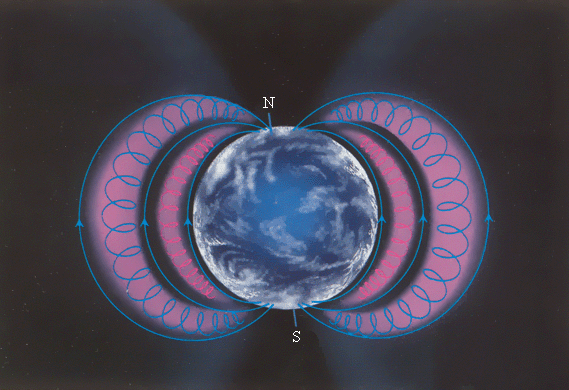
Рисунок 1.18.7. Радиационные пояса Земли. Быстрые заряженные частицы от Солнца, в основном электроны и протоны, попадают в магнитные ловушки радиационных поясов.

Возможно их вторжение в верхние слои атмосферы, служащее причиной возникновения «северных сияний».

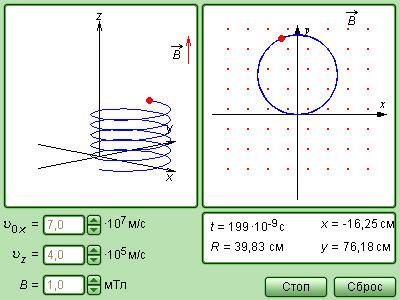
Рисунок 1.18.8. Модель движения заряда в магнитном поле.

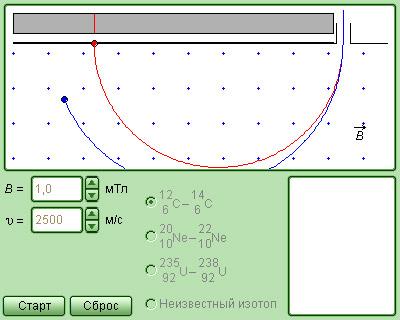
Рисунок 1.18.9. Модель Масс-спектрометра.

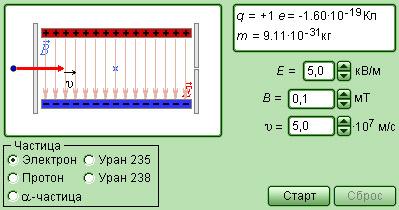
Рисунок 1.18.10. Модель селектора скоростей.

Всё ещё сложно?
Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

Определение и формула

Рис. 1. Выводы Лоренца

Обратите внимание на расположение векторов (рисунок слева, вверху). Векторы, указывающие направления скорости и силы Лоренца, лежат в одной плоскости XOY, причём они расположены под углом 90º. Вектор магнитной индукции сориентирован вдоль оси Z, перпендикулярной плоскости XOY, а значит, в выбранной системе координат он перпендикулярен к векторам силы и скорости

По закону Ампера:

Учитывая, что

Модуль F вычисляется по формуле:

Из формулы следует:

Сила Лоренца приобретает максимальное значение, если угол α прямой.
Если точечный заряд, например, электрон, попадает в среду однородного магнитного поля, обладая некой начальной скоростью, перпендикулярной к линиям электромагнитной индукции, тогда вектор F будет перпендикулярен к вектору скорости. На точечный заряд будет действовать центробежная сила, которая заставит его вращаться по кругу. При этом работа равняется нулю (см. рис.2).
Если угол между вектором индукции и скоростью частицы не равняется 90º, тогда заряд будет двигаться по спирали. Направление вращения зависит от полярности заряда (рис. 3).

Рис. 2. Заряженная частица между полюсами магнитовРис. 3. Ориентация вектора в зависимости от полярности заряда

Из рисунка 3 видно, что вектор F направлен в противоположную сторону, если знак заряда меняется на противоположный (при условии, что направления остальных векторов остаются неизменными).

В чём измеряется?

Когда возникает?

Для возникновения силы Лоренца необходимо выполнить три условия:

У частицы должен быть отрицательный или положительный заряд.
Заряженная частица должна находиться в магнитном поле.
Частица должна быть в движении, то есть вектор v ≠ 0.

Если хотя бы одно из условий не выполняется, сила Лоренца не возникает.

Подключение к карте палатки

Воспроизведение результатов Лоренца, созданных в системе Mathematica . Точки над красной линией соответствуют лепесткам переключения системы.

На рисунке 4 своей статьи Лоренц построил относительное максимальное значение в направлении z, полученное системой, против предыдущего относительного максимума в направлении z. Эта процедура позже стала известна как карта Лоренца (не путать с графиком Пуанкаре , который отображает пересечения траектории с заданной поверхностью). Полученный участок имеет форму, очень похожую на карту палатки . Лоренц также обнаружил, что когда максимальное значение z выше определенного порогового значения, система переключится на следующий лепесток. Объединив это с хаосом, который, как известно, демонстрируется картой палатки, он показал, что система переключается между двумя лепестками хаотично.

Значение и определение

Закон силы Лоренца описывает влияние E и B на точечный заряд, но такое воздействие не показывает всю картину. Заряженные частицы не просто дрейфуют в однородном электромагнитном поле. Возможно, они подвергаются и другим воздействиям, например, гравитации. В реальных материалах выводы физика не подходят для описания коллективного поведения таких частиц, как в принципе и для вычисления, поскольку тела не только реагируют на поля E и B, но и генерируют их.

Сложные уравнения переноса должны решаться для определения временной и пространственной реакции зарядов, например, равенств:

Больцмана;
Фоккера — Планка;
Навье — Стокса.

Для большей точности следует пояснить, что под силой Лоренца понимается следующее эмпирическое утверждение: F на пробном заряде в данной точке и данном времени является определённой функцией заряда q и скорости V, которая может быть параметризована ровно двумя векторами E и B в форме F = q (E + v x B).

Это справедливо даже для частиц, приближающихся к скорости света. Таким образом, два векторных поля (магнитное и электрическое) определяются во всём пространстве и времени относительно того, какую силу получит испытательный заряд.

Собственно, это только определение в принципе, потому что реальная частица (в отличие от гипотетической) будет генерировать собственные конечные поля E и B, изменяющие электромагнитную силу, которую он испытывает. Кроме того, когда у заряда есть ускорение, как если бы он был вынужден двигаться по искривлённой какими-либо внешними агентами траектории, от него исходит излучение, вызывающие торможение. Эти эффекты происходят как через прямое воздействие, так и косвенное. Помимо прочего, нужно учитывать гравитацию и другие силы.

Сила лоренца просто и понятно: определение, формула, правило левой руки

История

Усиление и движущая ЭДС

Сила тяжести: формула

Определение[править | править код]

Действие магнитного поля на движущийся заряд. Сила Лоренца

Примеры из жизни

Насколько вы сильны?

Определение и формула

В чём измеряется?

Когда возникает?

Урок физики в 9 классе по теме : » Решение задач по теме : «Сила Ампера. Сила Лоренца»»

Теория Лоренца

Применение силы Лоренца в технике

Кинескоп

Масс-спектрограф

Циклотрон

Магнетрон

Магнитное поле Земли

Формула силы трения

Магнитное поле

Определение и формула

В чём измеряется?

Когда возникает?

Подключение к карте палатки

Значение и определение

Похожие записи: