Сила лоренца правило левой руки

Частные случаи (примеры применения)[править | править код]

В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частица будет равномерно двигаться по окружности постоянного радиуса rr
. Сила Лоренца в этом случае является центростремительной силой:
mv2r=|q|vB⇒r=m|q|⋅vB{mv^2\over r} = |q|vB\Rightarrow r = {m\over |q|}\cdot{v\over B}
(в СИ)
mv2r=|q|cvB⇒r=cm|q|⋅vB{mv^2\over r} = {|q|\over c}vB\Rightarrow r = {cm\over |q|}\cdot{v\over B}
(в СГС)

При скорости vv
намного меньшей скорости света период TT
не зависит от vv
:
T=2πB⋅m|q|T = {2\pi\over B}\cdot{m\over |q|}
(в СИ)
T=2πB⋅mc|q|T = {2\pi\over B}\cdot{mc\over |q|}
(в СГС)

Если заряженная частица движется в магнитном поле так, что вектор скорости vv
составляет с вектором магнитной индукции BB
угол α\alpha
, то траекторией движения частицы является винтовая линия с радиусом rr
и шагом винта hh
:
r=m|q|⋅vsin Синус αB,r = {m\over |q|}\cdot{v\sin\alpha\over B},h=2πB⋅m|q|⋅vcos Косинус αh = {2\pi\over B}\cdot{m\over |q|}\cdot v\cos\alpha
(в СИ)
r=mc|q|⋅vsin Синус αB,r = {mc\over |q|}\cdot{v\sin\alpha\over B},h=2πB⋅mc|q|⋅vcos Косинус αh = {2\pi\over B}\cdot{mc\over |q|}\cdot v\cos\alpha
(в СГС)

Сила Лоренца используется в телевизионных электронно-лучевых трубках, а также в масс-спектрометрии.

Теория Лоренца

Хендрик Антон Лоренц

В 1892 г. голландский физик-теоретик Хендрик Антон Ло́ренц опубликовал работу «Электромагнитная теория Максвелла и её применение к движущимся телам», в которой объединил теорию поля и созданную им теорию электронного строения вещества. Лоренц предположил, что все молекулы вещества состоят из частиц, имеющих электрический заряд. Величина этих зарядов одинакова. Но одни из них заряжены отрицательно, другие положительно. Все эти элементарные заряды создают микроскопические электромагнитные поля, которые описываются уравнениями Максвелла.

Конечно, теория Лоренца имела недостатки и отличалась от современной электронной теории. Но в этой работе учёный вывел формулу силы, действующей на электрический заряд со стороны электромагнитного поля. Эту силу впоследствии назвали силой Лоренца.

Но что же такое электрический ток? Это направленное движение электрических зарядов. И если на каждую заряженную частицу действует сила Лоренца, то на отрезок проводника с током в электромагнитном поле должна действовать сила, величина которой равна сумме всех сил Лоренца, действующих на заряды, образующие электрический ток в проводнике.

И такая сила была открыта задолго до Лоренца. Ещё не зная о существовании силы, действующей на отдельный электрический заряд, французский физик Мари Андре Ампер в 1820 г. описал силу, действующую со стороны электромагнитного поля на проводник с током. Её назвали силой Ампера.

Как связано магнитное поле с Буравчиком и руками

Рассматривая движение полей токовой и магнитной природы, можно легко проследить взаимную связь правила Буравчика с канонами правой и левой руки. Для более качественного сравнения этих понятий, следует рассмотреть, что они представляют собой по отдельности.

Закон Буравчика точно устанавливает направленность напряженности, вызываемой магнитными полями. При этом само поле должно размещаться в прямом направлении по отношению к проводящему материалу с электротоком.

Для более полного представления берется штопор с правой резьбой и ввинчивается по часовой стрелочке в сторону протекания тока. Направленность магнетических полей соответствует правостороннему движению штопорной рукоятки.

Правило правой руки может рассматриваться в двух вариантах. В одном из них пальцы, согнутые в кулак, охватывают неподвижный токопроводник. Они обозначают, в какую сторону смотрит вектор магнитных линий, который, как и у рукоятки Буравчика, будет по ходу часовой стрелки. Самый крупный палец отступает на 90º и показывает, в какую сторону движется ток.

Если же токопровод движется, то правая рука размещается иным способом. Ладонь устанавливается между северным и южным полюсами так, чтобы она была в перпендикулярности с силовыми линиями, проходящими через нее. Крупный палец фиксируется в вертикальном положении и показывает в сторону направленного движения проводника. Оставшиеся пальцы, протянутые вперед, смотрят в ту же сторону, что и индукционный ток. Эта установка нашла свое применение в расчетах катушечных соленоидов, оказывающих воздействие на физические свойства тока.

Отделяя друг от друга правило правой и левой руки, их физика показывает, что второй вариант, используемый в расчетах, действует по-другому. Левая ладошка размещается в таком положении, чтобы четыре пальца были направлены в сторону тока, продвигающегося по проводнику. Магнитные линии, перемещаясь от одного полюса к другому, заходят в ладошку под 90 градусов. Оттопыренный крупный палец смотрит в ту же сторону, что и сила, воздействующая на токопроводник.

Какое правило применить

Слова синонимы: рука, винт, буравчик

Вначале разберем слова-синонимы, многие начали спрашивать себя: если тут повествование должно затрагивать буравчик, почему текст постоянно касается рук. Введем понятие правой тройки, правой системы координат. Итого, 5 слов-синонимов.

Потребовалось выяснить векторное произведение векторов, оказалось: в школе это не проходят. Проясним ситуацию любознательным школьникам.

Декартова система координат

Школьные графики на доске рисуют в декартовой системе координат Х-Y. Горизонтальная ось (положительная часть) направлена вправо – надеемся, вертикальная – указывает вверх. Делаем один шаг, получая правую тройку. Представьте: из начала отсчета в класс смотрит ось Z. Теперь школьники знают определение правой тройки векторов.

В Википедии написано: допустимо брать левые тройки, правые, вычисляя векторное произведение, несогласны. Усманов в этом плане категоричен. С разрешения Александра Евгеньевича приведем точное определение: векторным произведением векторов называют вектор, удовлетворяющий трем условиям:

1. Модуль произведения равен произведению модулей исходных векторов на синус угла меж ними.
2. Вектор результата перпендикулярен исходным (вдвоем образуют плоскость).
3. Тройка векторов (по порядку упоминания контекстом) правая.

Правую тройку знаем. Итак, если ось Х – первый вектор, Y – второй, Z будет результатом. Почему назвали правой тройкой? По-видимому, связано с винтами, буравчиками. Если закручивать воображаемый буравчик по кратчайшей траектории первый вектор-второй вектор, поступательное движение оси режущего инструмента станет происходить в направлении результирующего вектора:

1. Правило буравчика применяется к произведению двух векторов.
2. Правило буравчика качественно указывает направление результирующего вектора этого действия. Количественно длина находится выражением, упомянутым (произведение модулей векторов на синус угла меж ними).

Простые приемы запоминания правил буравчика

Люди забывают, что силу Лоренца проще определять правилом буравчика с левосторонней резьбой. Желающий понять принцип действия электрического двигателя должен как дважды два щелкать подобные орешки. В зависимости от конструкции число катушек ротора бывает значительным, либо схема вырождается, становясь беличьей клеткой. Ищущим знания помогает правило Лоренца, описывающее магнитное поле, где движутся медные проводники.

Для запоминания представим физику процесса. Допустим, движется электрон в поле. Применяется правило правой руки для нахождения направления действия силы. Доказано: частица несет отрицательный заряд. Направление действия силы на проводник находится правилом левой руки, вспоминаем: физики совершенно с левых ресурсов взяли, что электрический ток течет в направлении противоположном тому, куда направились электроны. И это неправильно. Поэтому приходится применять правило левой руки.

Не всегда следует идти такими дебрями. Казалось бы, правила больше запутывают, не совсем так. Правило правой руки часто применяется для вычисления угловой скорости, которая является геометрическим произведением ускорения на радиус: V = ω х r. Многим поможет визуальная память:

1. Вектор радиуса круговой траектории направлен из центра к окружности.
2. Если вектор ускорения направлен вверх, тело движется против часовой стрелки.

https://youtube.com/watch?v=enwbrdUcbvU

Посмотрите, здесь опять действует правило правой руки: если расположить ладонь так, чтобы вектор ускорения входил перпендикулярно в ладонь, персты вытянуть по направлению радиуса, отогнутый на 90 градусов большой палец укажет направление движения объекта. Достаточно однажды нарисовать на бумаге, запомнив минимум на половину жизни. Картинка действительно простая. Больше на уроке физики не придется ломать голову над простым вопросом – направление вектора углового ускорения.

Аналогичным образом определяется момент силы. Исходит перпендикулярно из оси плеча, совпадает направлением с угловым ускорением на рисунке, описанном выше. Многие спросят: зачем нужно? Почему момент силы не скалярная величина? Зачем направление? В сложных системах непросто проследить взаимодействия. Если много осей, сил, помогает векторное сложение моментов. Можно значительно упростить вычисления.

Сила в физике

Сила – мера взаимодействия тел. Взаимное действие тел друг на друга полностью описывает процессы, связанные с изменением скорости или деформацией тел.

Как физическая величина сила имеет единицу измерения (в системе СИ – Ньютон) и прибор для ее измерения – динамометр. Принцип действия силомера основан на сравнении силы, действующей на тело, с силой упругости пружины динамометра.

За силу в 1 ньютон принята сила, под действием которой тело массой 1 кг изменяет свою скорость на 1 м за 1 секунду.

Сила как векторная величина определяется:

• направлением действия;
• точкой приложения;
• модулем, абсолютной величиной.

Описывая взаимодействие, обязательно указывают эти параметры.

Виды природных взаимодействий: гравитационные, электромагнитные, сильные, слабые. Гравитационные силы (сила всемирного тяготения с ее разновидностью – силой тяжести) существуют благодаря влиянию гравитационных полей, окружающих любое тело, имеющее массу. Исследование полей гравитации не закончено до сих пор. Найти источник поля пока не представляется возможным.

Больший ряд сил возникает вследствие электромагнитного взаимодействия атомов, из которых состоит вещество.

Магнитное поле. Магнитная индукция. Правила буравчика и правой руки. Сила Ампера. Правило левой руки

Подробности

Просмотров: 532

– это особый вид материи, посредством которой осуществляется взаимодействие между движущимися электрически заряженными частицами.

Свойства стационарного магнитного поля

Постоянное (или стационарное) магнитное поле – это магнитное поле, неизменяющееся во времени .

1. Магнитное поле создается движущимися заряженными частицами и телами, проводниками с током, постоянными магнитами.

2. Магнитное поле действует на движущиеся заряженные частицы и тела, на проводники с током, на постоянные магниты, на рамку с током.

3. Магнитное поле вихревое, т.е. не имеет источника.

Магнитные силы

– это силы, с которыми проводники с током действуют друг на друга.

………………

Магнитная индукция

– это силовая характеристика магнитного поля.

Вектор магнитной индукции направлен всегда так, как сориентирована свободно вращающаяся магнитная стрелка в магнитном поле.

Единица измерения магнитной индукции в системе СИ:

– это линии, касательными к которой в любой её точке является вектор магнитной индукции.

Однородное магнитное поле – это магнитное поле, у которого в любой его точке вектор магнитной индукции неизменен по величине и направлению; наблюдается между пластинами плоского конденсатора, внутри соленоида (если его диаметр много меньше его длины) или внутри полосового магнита.

Магнитное поле прямого проводника с током:

или

где

– направление тока в проводнике на нас перпендикулярно плоскости листа,

– направление тока в проводнике от нас перпендикулярно плоскости листа.

Магнитное поле соленоида:

Магнитное поле полосового магнита:

– аналогично магнитному полю соленоида.

Свойства линий магнитной индукции

– имеют направление;
– непрерывны;
-замкнуты (т.е. магнитное поле является вихревым);
– не пересекаются;
– по их густоте судят о величине магнитной индукции.

Направление линий магнитной индукции

– определяется по правилу буравчика или по правилу правой руки.

Правило буравчика ( в основном для прямого проводника с током):

Если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением линий магнитного поля тока.

Правило правой руки

( в основном для определения направления магнитных линий внутри соленоида):

Если обхватить соленоид ладонью правой руки так, чтобы четыре пальца были направлены вдоль тока в витках, то отставленный большой палец покажет направление линий магнитного поля внутри соленоида.

Существуют другие возможные варианты применения правил буравчика и правой руки.

Сила Ампера

– это сила, с которой магнитное поле действует на проводник с током.

Модуль силы Ампера равен произведению силы тока в проводнике на модуль вектора магнитной индуции, длину проводника и синус угла между вектором магнитной индукции и направлением тока в проводнике.

Сила Ампера максимальна, если вектор магнитной индукции перпендикулярен проводнику.

Если вектор магнитной индукции параллелен проводнику, то магнитное поле не оказывает никакого действия на проводник с током, т.е. сила Ампера равна нулю.

Направление силы Ампера определяется по правилу левой руки:

Если левую руку расположить так, чтобы перпендикулярная проводнику составляющая вектора магнитной индукции входила в ладонь, а 4 вытянутых пальца были направлены по направлению тока, то отогнутый на 90 градусов большой палец покажет направление силы, действующий на проводник с током.

Примеры:

или

Действие магнитного поля на рамку с током

Однородное магнитное поле ориентирует рамку (т.е. создается вращающий момент и рамка поворачивается в положение, когда вектор магнитной индукции перпендикулярен плоскости рамки).

Неоднородное магнитное поле ориентирует + притягивает или отталкивает рамку с током.
Так, в магнитном поле прямого проводника с током (оно неоднородно) рамка с током ориентируется вдоль радиуса магнитной линии и притягивается или отталкивается от прямого проводника с током в зависимости от направления токов.

Следующая страница «Действие магнитного поля на движущийся заряд.Магнитные свойства вещества»

Назад в раздел «10-11 класс»

Электромагнитное поле – Класс!ная физика

Взаимодействие токов. Магнитное поле. Вектор магнитной индукции. Сила Ампера —
Действие магнитного поля на движущийся заряд.Магнитные свойства вещества —
Явление электромагнитной индукции. Магнитный поток. Направление индукционного тока. Правило Ленца —
ЭДС электромагнитной индукции. Вихревое электрическое поле —
ЭДС индукции в движущихся проводниках —
Самоиндукция. Индуктивность. Энергия магнитного поля. Вопросы к пр/работе

Сила упругости

При изменении формы тела (его деформации) появляется сила, которая стремится вернуть телу его первоначальную форму. Этой силе дали название «сила упругости». Возникает она вследствие электрического взаимодействия частиц, из которых состоит тело.

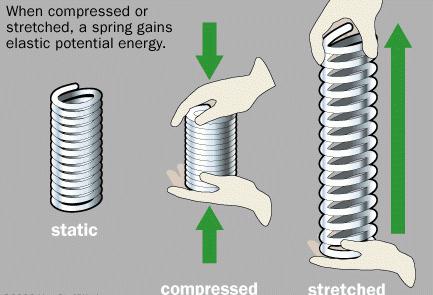
Рассмотрим простейшую деформацию: растяжение и сжатие. Растяжение сопровождается увеличением линейных размеров тел, сжатие – их уменьшением. Величину, характеризующую эти процессы, называют удлинением тела. Обозначим ее «x». Формула силы упругости напрямую связана с удлинением. Каждое тело, подвергающееся деформации, имеет собственные геометрические и физические параметры. Зависимость упругого сопротивления деформации от свойств тела и материала, из которого оно изготовлено, определяется коэффициентом упругости, назовем его жесткостью (k).

Математическая модель упругого взаимодействия описывается законом Гука.

Сила, возникающая при деформации тела, направлена против направления смещения отдельных частей тела, прямо пропорциональна его удлинению:

Fy = -kx (в векторной записи).

Знак «-» говорит о противоположности направления деформации и силы.

В скалярной форме отрицательный знак отсутствует. Сила упругости, формула которой имеет следующий вид Fy = kx, используется только при упругих деформациях.

Уравнение (единицы СИ)

Заряженная частица

Силой F действующий на частицу электрического заряда q с мгновенной скоростью v, из-за внешнего электрического поля E и магнитного поля B, дают:

где векторный продукт креста. Все жирные количества – векторы. Более явно заявленный:

в котором r – вектор положения заряженной частицы, t – время, и сверхточка – производная времени.

Положительно заряженная частица будет ускорена в той же самой линейной ориентации как область E, но изогнется перпендикулярно и к мгновенному скоростному вектору v и к области B согласно правому правилу (подробно, если большой палец правых пунктов вдоль v и указательный палец вдоль B, то средний палец указывает вдоль F).

Термин qE называют электрической силой, в то время как термин qv B называют магнитной силой. Согласно некоторым определениям, термин «сила Лоренца» относится определенно к формуле для магнитной силы с полной электромагнитной силой (включая электрическую силу) данный некоторое другое (нестандартное) имя. Эта статья не будет следовать этой номенклатуре: В дальнейшем термин «сила Лоренца» отнесется только к выражению для полной силы.

Магнитный компонент силы силы Лоренца проявляется как сила, которая действует на находящийся под напряжением провод в магнитном поле. В том контексте это также называют лапласовской силой.

Непрерывное распределение обвинения

Для непрерывного распределения обвинения в движении уравнение силы Лоренца становится:

где dF – сила на маленькой части распределения обвинения с обвинением dq. Если обе стороны этого уравнения разделены на объем этой маленькой части распределения обвинения dV, результат:

где f – плотность силы (сила за единичный объем), и ρ – плотность обвинения (обвинение за единичный объем). Затем, плотность тока, соответствующая движению континуума обвинения, является

таким образом, непрерывный аналог уравнению –

Полная сила – интеграл объема по распределению обвинения:

Устраняя ρ и J, используя уравнения Максвелла и управляя использованием теорем векторного исчисления, эта форма уравнения может использоваться, чтобы получить тензор напряжения Максвелла σ, в свою очередь это может быть объединено с вектором Пойнтинга S, чтобы получить электромагнитный тензор энергии напряжения T используемый в Общей теории относительности.

С точки зрения σ и S, другим способом написать силу Лоренца (за единицу 3-й объем) является

где c – скорость света и ∇ · обозначает расхождение области тензора. Вместо суммы обвинения и его скорости в электрических и магнитных полях, это уравнение связывает энергетический поток (поток энергии в единицу времени за расстояние единицы) в областях к силе, проявленной на распределении обвинения. Дополнительную информацию см. в Ковариантной формулировке классического электромагнетизма.

Физическая основа правил

Прогнозирование направления плотности потока ( B ), учитывая, что ток I течет в направлении большого пальца.

Когда электроны или любые заряженные частицы текут в одном и том же направлении (например, как электрический ток в электрическом проводнике , таком как металлический провод ), они создают цилиндрическое магнитное поле , охватывающее проводник (как обнаружил Ганс Кристиан Эрстед. ).

Направление индуцированного магнитного поля можно запомнить по правилу штопора Максвелла . То есть, если обычный ток течет от наблюдателя, магнитное поле движется по часовой стрелке вокруг проводника в том же направлении, в котором штопор должен был бы повернуться, чтобы уйти от наблюдателя. Направление индуцированного магнитного поля также иногда запоминается правилом для правой руки , как показано на иллюстрации, с большим пальцем, показывающим направление обычного тока, и пальцами, показывающими направление магнитного поля. Существование этого магнитного поля может быть подтверждено размещением магнитных компасов в различных точках по периферии электрического проводника, по которому проходит относительно большой электрический ток.

Большой палец показывает направление движения, указательный палец показывает линии поля, а средний палец показывает направление индуцированного тока.

Если внешнее магнитное поле приложено горизонтально, так что оно пересекает поток электронов (в проводнике или в электронном пучке), два магнитных поля будут взаимодействовать. Майкл Фарадей представил для этого визуальную аналогию в виде воображаемых магнитных силовых линий : те, что в проводнике, образуют концентрические круги вокруг проводника; те, которые находятся во внешнем магнитном поле, идут параллельными линиями. Если те, которые находятся на одной стороне проводника, движутся (от северного магнитного полюса к южному) в направлении, противоположном тем, которые окружают проводник, они будут отклонены так, что они пройдут с другой стороны проводника (потому что магнитные силовые линии не могут пересекаются или бегут друг против друга). Следовательно, будет большое количество силовых линий магнитного поля в небольшом пространстве на этой стороне проводника и их недостаток на исходной стороне проводника. Поскольку силовые линии магнитного поля больше не являются прямыми линиями, а изогнуты, чтобы проходить вокруг электрического проводника, они находятся под напряжением (как растянутые эластичные ленты), а энергия связана в магнитном поле. Так как это энергетическое поле сейчас в основном не встречает сопротивления, его наращивание или вытеснение в одном направлении создает — аналогично третьему закону движения Ньютона — силу в противоположном направлении. Поскольку в этой системе есть только один подвижный объект (электрический проводник), на который действует эта сила, результирующий эффект представляет собой физическую силу, работающую, чтобы вытеснить электрический проводник из внешнего магнитного поля в направлении, противоположном тому, на которое магнитный поток перенаправляется на — в этом случае (двигатели), если проводник проводит обычный ток вверх , а внешнее магнитное поле перемещается от наблюдателя, физическая сила будет толкать проводник влево . Это причина крутящего момента в электродвигателе. (Электродвигатель затем сконструирован так, что выталкивание проводника из магнитного поля заставляет его помещаться в следующее магнитное поле, и это переключение продолжается бесконечно.)

Закон Фарадея : индуцированная электродвижущая сила в проводнике прямо пропорциональна скорости изменения магнитного потока в проводнике.

Примеры из жизни

Насколько вы сильны?

Рассмотрим простейший пример. Ваш ребёнок сел на санки и просит вас его покатать. С какой силой вам нужно тянуть эти санки, чтобы ребёнок остался доволен быстрой ездой ? Пока санки с ребёнком остаются в состоянии покоя, все силы, действующие на них, уравновешены. Состояние покоя — это частный случай инерции. Здесь на санки действуют две силы: тяжести Fт = m•g, направленная вертикально вниз, и нормального давления N, направленная вертикально вверх. Поскольку санки не движутся, то N – m•g = 0. Тогда из этого равенства следует, что N = m•g.

Когда вы решили покатать своего ребёнка, вы прикладываете силу тяги (Fтяги) к санкам с ребёнком. Когда вы начинаете тянуть санки, возникает сопротивление движению, вызванное силой трения (Fтр.), направленной в противоположную сторону. Это так называемая сила трения покоя. Когда тело не движется, она равна нулю. Стоит потянуть за санки — и появляется сила трения покоя, которая меняется от нуля до некоторого максимального значения (Fтр. max). Как только Fтяги превысит Fтр.max, санки с ребёнком придут в движение.

Чтобы найти Fтяги, применим второй закон Ньютона: Fтяги – Fтр.max = m•a, где a – ускорение, с которым вы тянете санки, m – масса санок с ребёнком. Допустим, вы разогнали санки до определённой скорости, которая не изменяется. Тогда a = 0 и вышеприведённое уравнение запишется в виде: Fтяги – Fтр. max = 0, или Fтяги = Fтр.max. Есть известный закон из физики, который устанавливает определённую зависимость для Fтр.max и N. Эта зависимость имеет вид: Fтр.max = fmax • N, где fmax – максимальный коэффициент трения покоя.

Если в эту формулу подставить выражение для N, то мы получим Fтр.max = fmax•m•g. Тогда формула искомой силы тяги примет вид: Fтяги = fmax•m•g = fск•m•g, где fск = fmax – коэффициент трения скольжения, g – ускорение свободного падения. Допустим, fск = 0,7, m = 30 кг, g = 9,81 м/с², тогда Fтяги = 0,7 • 30 кг • 9,81 м/с² = 206,01 Н (Ньютона).

Сила Лоренца. Движение зарядов в магнитном поле

Электрические заряды, движущиеся в определенном направлении, создают вокруг себя магнитное поле, скорость распространения которого в вакууме равно скорости света, а в других средах чуть меньше. Если движение заряда происходит во внешнем магнитном поле, то между внешним магнитным полем и магнитным полем заряда возникает взаимодействие. Так как электрический ток – это направленное движение заряженных частиц, то сила, которая будет действовать в магнитном поле на проводник с током, будет являться результатом отдельных (элементарных) сил, каждая из которых прикладывается к элементарному носителю заряда.

Процессы взаимодействия внешнего магнитного поля и движущихся зарядов исследовались Г. Лоренцом, который в результате многих своих опытов вывел формулу для расчета силы, действующей на движущуюся заряженную частицу со стороны магнитного поля. Именно поэтому силу, которая действует на движущийся в магнитном поле заряд, называют силой Лоренца.

Сила, действующая на проводник стоком (из закона Ампера), будет равна:

По определению сила тока равна I = qn (q – заряд, n – количество зарядов, проходящее через поперечное сечение проводника за 1 с). Отсюда следует:

Где: n0 – содержащееся в единице объема количество зарядов, V – их скорость движения, S – площадь поперечного сечения проводника. Тогда:

Подставив данное выражение в формулу Ампера, мы получим:

Данная сила будет действовать на все заряды, находящиеся в объеме проводника: V = Sl. Количество зарядов, присутствующих в данном объеме будет равно:

Тогда выражение для силы Лоренца будет иметь вид:

Отсюда можно сделать вывод, что сила Лоренца, действующая на заряд q, который двигается в магнитном поле, пропорциональна заряду, магнитной индукции внешнего поля, скорости его движения и синусу угла между V и В, то есть:

За направление движения заряженных частиц принимают направление движения положительных зарядов. Поэтому направление данной силы может быть определено с помощью правила левой руки.

Сила, действующая на отрицательные заряды, будет направлена в противоположную сторону.

Сила Лоренца всегда направлена перпендикулярно скорости V движения заряда и поэтому работу она не совершает. Она изменяет только направление V, а кинетическая энергия и величина скорости заряда при его движении в магнитном поле остаются неизменными.

Когда заряженная частица движется одновременно в магнитном и электрическом полях, на него будет действовать сила:

Где Е – напряженность электрического поля.

Рассмотрим небольшой пример:

Электрон, прошедший ускоряющую разность потенциалов 3,52∙103 В, попадает в однородное магнитное поле перпендикулярно линиям индукции. Радиус траектории r = 2 см, индукция поля 0,01 Т. Определить удельный заряд электрона.

Решение:

Удельный заряд – это величина, равная отношению заряда к массе, то есть e/m.

В магнитном поле с индукцией В на заряд, движущийся со скоростью V перпендикулярно линиям индукции, действует сила Лоренца FЛ = BeV. Под ее действием заряженная частица будет перемещаться по дуге окружности. Так как при этом сила Лоренца вызовет центростремительное ускорение, то согласно 2-му закону Ньютона можно записать:

Кинетическую энергию, которая будет равна mV2/2, электрон приобретает за счет работы А сил электрического поля (А = eU), подставив в уравнение получим:

Преобразовав эти соотношения и исключив из них скорость, получим формулу для определения удельного заряда электрона:

Подставив исходные данные, выраженные в СИ, получим:

Проверяем размерность:

И кому интересно — видео о движении заряженных частиц:

Похожие материалы:

• Сила тока. Электродвижущая сила. Разность потенциалов
• Основные законы для электрических зарядов
• Как контроллер микрошагов обеспечивает более плавное…
• Электростатический диполь. Электростатическое поле.…
• Поле намагниченного вещества. Микроскопические…

Формулировка и формулы

Частица с зарядом q испытывает силу F, когда движется со скоростью v в электрическом (E) и магнитном (B) полях. Определяется она как F = qE + qv x B и измеряется в единицах СИ — N (ньютон). С точки зрения декартовых компонентов имеется:

• F x = q (E x + ⱴ y B z — ⱴ z B y);
• F y = q (E y + ⱴ z B x — ⱴ x B z);
• F z = q (E z + ⱴ x B y — ⱴ y B x).

Ускорение частицы будет происходить в той же линейной ориентации, что и поле E, но станет изгибаться перпендикулярно как вектору мгновенной скорости v, так и полю B. Это говорит о соответствии формулы силы Лоренца и «правила левой руки». Также здесь будет работать и «правило буравчика» (если пальцы расширяются, чтобы указывать в направлении v, а затем скручиваются, показывая в сторону B, тогда большой палец будет смотреть на F).

Комбинация q E называется электрической силой, а q (v + B) — магнитной. В этом контексте её можно называть силой Лапласа. Она не влияет на мощность, потому что всегда перпендикулярна скорости частицы.

Для непрерывного распределения заряда в движении уравнение принимает вид dE = dq (E + v + B). Если обе части равенства будут разделены на объём небольшого фрагмента dV, результат будет выглядеть следующим образом: f = p (E + v x B). Поэтому непрерывным аналогом уравнения является f = pE + J x B, где J — плотность тока.

Суммарная сила — интеграл объёма по распределению заряда: F = ∫∫∫ (p E + J x B) dV. Устраняя p и J, используя уравнения Максвелла и манипулируя с помощью теорем векторного исчисления, эту форму можно использовать для получения тензора напряжения σ. В свою очередь, это можно объединить с вектором Пойнтинга s для получения электромагнитного тензора энергии-импульса T, используемого в общей теории относительности. Если разделить полный заряд и ток на их связанные частицы, то получится плотность силы Лоренца. Она, в свою очередь, может объяснить крутящий момент.

Урок физики в 9 классе по теме : » Решение задач по теме : «Сила Ампера. Сила Лоренца»»

Тема урока:

«Решение задач по теме «Сила Ампера. Сила Лоренца».

Место урока в системе уроков по теме:

На предыдущем уроке обучающиеся получили знания о векторе магнитной индукции, силе Ампера, силе Лоренца. Данный урок позволяет отработать навыки решения задач по формуле силы Ампера и силы Лоренца .

Цель урока:

показать теоретическую значимость закона Ампера при решении задач, научить применять полученные знания при решении задач.

Задачи урока:

• Дидактическая

  – создавать условия для усвоения нового учебного материала через проблемно-деятельностный подход.

• Образовательная

  – рассмотреть применение закона Ампера в ходе решения различных задач.

• Развивающая

  – развивать логическое мышление обучающихся при решении задач на расчёт силы Амперы и силы Лоренца.

• Воспитательная

  – прививать культуру умственной деятельности.

Планируемые результаты.

Обучающиеся должны:

• овладеть алгоритмом решения задач по данной теме.
• уметь решать задачи с применением закона Ампера, формулы для нахождения силы Лоренца .

Техническое обеспечение урока:

1. Компьютер, проектор, экран.

Дополнительное методическое и дидактическое обеспечение урока:

1. Презентация к уроку.
2. Карточки с задачами.

Мобилизующее начало урока («исходная мотивация»). Позитивный настрой на урок.

“Умение решать задачи — это практическое

искусство, подобное плаванию или катанию

на лыжах, или игре на фортепиано: научиться

этому можно, лишь подражая избранным

образцам и постоянно тренируясь”

Д. Пойа

В данной теме рассмотрим основные типы задач, а также попытаемся выделить общую методику их решений. В представленной теме можно выделить три типа задач:

1) на расчет полей (вычисление магнитной индукции, в какой либо точке магнитного поля);

2) о силовом действии магнитного поля на проводники или контур с током;

3) о силовом действии магнитного поля на движущиеся в нем заряженные частицы.

1.Фронтальный опрос:

1.Как называют физ. Величину характеризующую магнитное поле?

2. Какой буквой обозначают?

3. В каких единицах измеряют?

4. Что означает 1 Тл?

5.Какую силу называют силой Ампера? Запишите на доске формулу для расчёта Силы Ампера.

6. Как определяется направление силы Ампера? Сформулируйте правило левой руки.

7.Чему равен модуль вектора магнитной индукции?

8. Какую силу называют силой Лоренца? Запишите на доске формулу для расчёта Силы Лоренца

9. Как определяется направление силы Лоренца? Сформулируйте правило левой руки.

2. Решение задач :

Задача 1 Определить силу, с которой однородное магнитное поле действует на проводник длиной 20 см, если сила тока в нем 300 мА, расположенный под углом 45 градусов к вектору магнитной индукции. Магнитная индукция составляет 0,5 Тл.

Задача 2 Проводник с током 5 А находится в магнитном поле с индукцией 10 Тл. Определить длину проводника, если магнитное поле действует на него с силой 20Н и перпендикулярно проводнику.

Задача 3 Определить силу тока в проводнике длиной 20 см, расположенному перпендикулярно силовым линиям магнитного поля с индукцией 0,06 Тл, если на него со стороны магнитного поля действует сила 0,48 Н.

Задача 4 Проводник длиной 20см с силой тока 50 А находится в однородном магнитном поле с индукцией 40 мТл. Какую работу совершит источник тока, если проводник переместится на 10 см перпендикулярно вектору магнитной индукции (вектор магнитной индукции перпендикулярен направлению тока в проводнике).

Задача 5 Определить силу, действующую на заряд 0,005 Кл, движущийся в магнитном поле с индукцией 0,3 Тл со скоростью 200 м/с под углом 45o к вектору магнитной индукции.

Задача 6 Какова скорость заряженного тела, перемещающегося в магнитном поле с индукцией 2 Тл, если на него со стороны магнитного поля действует сила 32 Н. Скорость и магнитное поле взаимно перпендикулярны. Заряд тела равен 0,5 мКл.

3.Самостоятельная работа по карточкам

4. Рефлексия

5. Д.з.

https://youtube.com/watch?v=eMa11WYguzk

https://youtube.com/watch?v=7IUpOAsKKvI

https://youtube.com/watch?v=mmAB-_2VYPk

Взаимодействие токов

Рассмотрим два случая. Первый – ток течет по прямому проводу. Второй – по круговому витку. Как мы знаем, ток создает магнитное поле.

В первом случае магнитная индукция провода с током I на расстоянии R от него считается по формуле:

Мю – магнитная проницаемость вещества, мю с индексом ноль – магнитная постоянная.

Во втором случае магнитная индукция в центре кругового витка с током равна:

Также при решении задач может пригодиться формула для магнитного поля внутри соленоида. Соленоид – это катушка, то есть множество круговых витков с током.

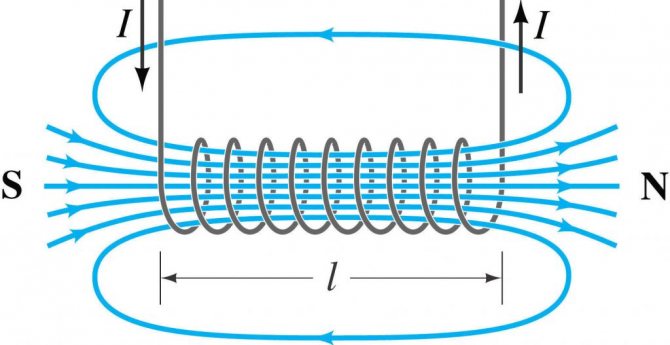
Пусть их количество – N, а длина самого соленоилда – l. Тогда поле внутри соленоида вычисляется по формуле:

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Похожие записи:

Тда 7377 даташит на русском Что такое эдс индукции и когда возникает? Задние фонари ваз 2107 Запуск синхронного двигателя с тиристорным Как по параметрам подобрать блок питания для компьютера Центральный замок с дистанционным управлением своими руками