Особенности включения
Для упрощения темы смешанного соединения резисторов решение задач следует ограничить схемами с подключением к источнику постоянного тока без реактивных компонентов. В этом случае можно исключить сложные колебательные процессы, сопряженные с циклами изменения потребления энергии в нагрузке. Для определения базовых зависимостей достаточно использовать классическую формулу закона Ома:
I (ток) = U (напряжение) / R (сопротивление).
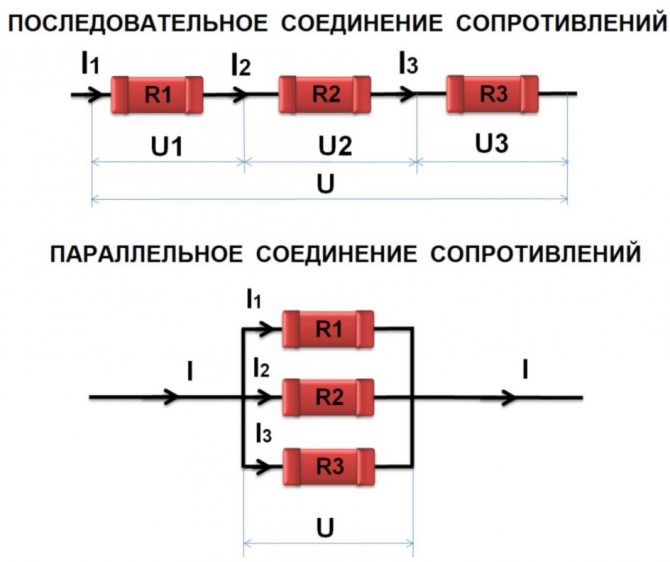
Основные виды соединений
На первой части рисунка показан последовательный проводник. Одинаковый ток можно измерить в любом разрыве с помощью мультиметра. Но даже без экспериментов понятно, что такой результат обеспечен единством пути его прохождения, который создан без разветвлений. Однако при установке разных резисторов (R1≠R2≠R3) напряжение на отдельных элементах отличается (U1≠U2≠U3). Суммарная величина будет равна потенциалу на клеммах источника питания (Uип = U1 + U2 + U3). Аналогичным образом вычисляют суммарное сопротивление:
Rобщ = R1 + R2 + R3.
Следующий пример – параллельное подключение. Здесь каждый ток проходит после разветвления по своему пути (ветке). По предыдущему алгоритму рассуждений несложно установить соответствующие зависимости:
- если R1≠R2≠R3, то I1≠I2≠I3;
- Iип = I1 + I2 + I3;
Если использовано параллельное соединение, формула для напряжений трансформируется в равенство:
Uип = U1 = U2 = U3.
К сведению. Другие виды соединений – это комбинации представленных вариантов. На отдельных участках цепи действительны рассмотренные выше правила.
Расчет сопротивления
В случае подключения деталей друг с другом, с применением параллельной схемы для расчета суммарного сопротивления, будет использоваться следующая формула:
R(общ)=1/(1/R1+1/R2+1/R3+1/Rn).
причем :
- R(общ) – суммарное значение сопротивления;
- R1- R3 и Rn – резисторы, подсоединенные по параллельной схеме.
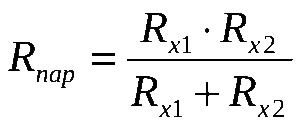Причем, если цепь создается на основе только двух элементов, то для определения суммарного номинального сопротивления следует использовать такую формулу:
R(общ)=R1*R2/R1+R2.
причем:
- R(общ) – суммарное сопротивление;
- R1 и R2 – резисторы, подсоединенные по параллельной схеме.
Видео: Пример расчёта сопротивления
https://youtube.com/watch?v=nEYXMjbZHbc
Универсальная схема расчета
Применительно к радиотехнике следует уделить внимание одному важному правилу: если подключаемые друг к другу элементы по параллельной схеме имеют одинаковый показатель, то для расчета суммарного номинала необходимо общее значение разделить на число подключенных узлов:
R(общ)=R1n.
причем :
- R(общ) – суммарное значение сопротивления;
- R – номинал резистора, подсоединенного по параллельной схеме;
- n – число подключенных узлов.
Особое внимание следует обратить на то, что конечный показатель сопротивления в случае использования параллельной схемы подключения обязательно будет меньше по сравнению с номиналом любого элемента, подключаемого в цепь
Последовательное соединение резисторов.
Последовательным называют соединение, при котором резисторы следуют друг за другом и образуют электрическую цепь из нескольких элементов, в которой конец одного резистора соединен с началом другого и т.д.
В последовательной цепи электрической ток поочередно протекает по всем резисторам и преодолевает сопротивление каждого из них. При этом ток в этой цепи одинаков. И если последовательно соединить два резистора R1 и R2, их общее (полное) сопротивление Rобщ будет равно сумме их сопротивлений. Это условие справедливо для любого числа резисторов, где:
Например.При соединении двух резисторов с номиналами R1 = 150 Ом и R2 = 330 Ом их общее сопротивление составит Rобщ = 150 + 330 = 480 Ом.
При соединении трех резисторов R1 = 20 кОм, R2 = 68 кОм и R3 = 180 кОм их общее сопротивление составит Rобщ = 20 + 68 + 180 = 268 кОм.
Запомните. Из нескольких соединенных последовательно резисторов их общее сопротивление Rобщ определяет тот, у которого сопротивление больше по отношению к другим резисторам в этой цепи.
Разница между последовательным и параллельным соединением, преимущества и недостатки
Принципиальные отличия между последовательным и параллельным соединение проводников по ключевым электротехническим параметрам приведены в таблице:
| Параметр/тип соединения | Последовательное | Параллельное |
| Электросопротивление | Равняется сумме электросопротивлений всех электропотребителей. | Меньше значения электросопротивления каждого отдельного из подключенных электроприборов. |
| Напряжение | Равняется совокупному вольтажу всех электропотребителей. | Одинаковая величина на всех участках электроцепи. |
| Сила тока | Одинаковая величина на всех участках электроцепи. | Равняется совокупному значению токов на каждом из приборов. |
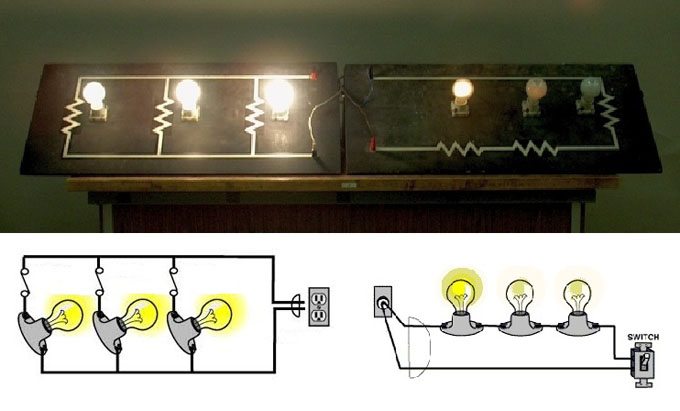
За счет своих особенностей каждый из типов сборки цепей имеет свои преимущества и недостатки. Это позволяет использовать данные способы для решения разных электротехнических задач.
Плюсы и минусы последовательного соединения
Основными преимуществам электроцепей из последовательно соединенных приборов являются их следующие особенности:
- простота проектирования и построения схемы;
- низкая стоимость комплектации;
- возможность подключения приборов, рассчитанных на меньшее рабочее напряжение, по сравнению с номинальным напряжением сети;
- выполнение функции регулирования тока – обеспечивает равномерные нагрузки на все приборы.
Однако у этого способа компоновки электросхемы есть и серьезные недостатки. Главным из них является ненадежность цепи из последовательно соединенных проводников. При выходе из строя любого из подключенных приборов, происходит отключение всей цепи.
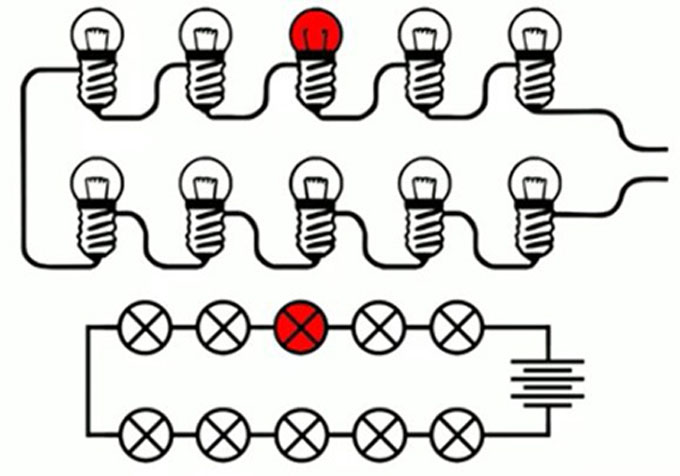
Кроме того, минусом является снижение напряжения при увеличении количества подключенных потребителей. Примером может служить последовательное соединение нескольких ламп. Чем больше осветительных приборов подключено таким способом к источнику электропитания, тем менее яркий свет они будут давать.
Плюсы и минусы параллельного соединения
При использовании параллельного соединения проводников обеспечиваются такой набор преимуществ:
- стабильность напряжения на электроприборах, вне зависимости от их числа;
- возможность включения или отключения отдельных участков в нужный момент без нарушения работы всей электроцепи;
- надежность – при выходе одного или нескольких компонентов из строя сама электроцепь продолжает сохранять работоспособность.
Недостатком является более сложный расчет и сложная схема, использование которой повышает стоимость комплектации электросети.
Не допускается подключение приборов, с номинальным рабочим вольтажом меньше сетевого. Параллельное соединение аккумуляторов с разным значением вольтажа связано с перетеканием тока в АКБ с меньшей его величиной, что может вызывать ускоренный износ батареи.
Что такое последовательное соединение проводников
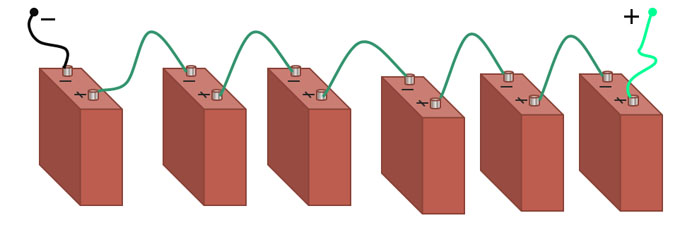
Суть этого способа заключается в том, что компоненты цепи подключаются друг к другу поочередно. Первый проводник одним проводом подключается к источнику питания. Второй его провод соединяется со вторым проводником, от которого идет конец на третий проводник и т.д., пока цепь не будет замкнута. Классическим примером последовательной электроцепи можно назвать подключение лампочек в гирлянде.
Ток проходит по цепи приборов, состоящей из резисторов, ламп или других нагрузок, протекая через каждый включенный в электроцепь прибор. В собранной таким способом цепи отсутствует эффект деления и накопления заряда на разных ее участках. Соответственно, физическая величина ампеража будет на всех участках одинаковой.
Совокупное электросопротивление всех последовательно соединенных нагрузок, приборов и устройств любого типа равняется сумме их индивидуальных сопротивлений. Таким образом, его значение прямо зависит от количества подключенных приборов и их параметров.
Аналогично рассчитывается и совокупный вольтаж. Он равняется сумме напряжений, действующих на каждом отдельном электроприборе.
Последовательное соединение проводников
Сопротивление при последовательном соединении проводников
Последовательное соединение проводников – это когда к одному проводнику мы соединяем другой проводник и так по цепочке. Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.
последовательное соединение резисторов
Чему же будет равняться их общее сопротивление? Оказывается, все просто. Оно будет равняться сумме всех сопротивлений проводников в этой цепи.
Получается, можно записать, что
формула при последовательном соединении резисторов
Пример
У нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.
Решение
Rобщее =R1 + R2 + R3 = 3+5+2=10 Ом.
То есть, как вы видите, цепочку из 3 резисторов мы просто заменили на один резистор RAB .
показать на реальном примере с помощью мультиметра Видео где подробно расписывается про эти соединения:
Сила тока через последовательное соединение проводников
Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома I=U/R.
Получается, если через резистор RAB течет какой-то определенный ток, следовательно, если разложить наш резистор на составляющие R1 , R2 , R3 , то получится, что через них течет та же самая сила тока, которая текла через резистор RAB .
сила тока через последовательное соединение проводников
Получается, что при последовательном соединении проводников сила тока, которая течет через каждый проводник одинакова. То есть через резистор R1 течет такая же сила тока, как и через резистор R2 и такая же сила тока течет через резистор R3 .
Напряжение при последовательном соединении проводников
Давайте еще раз рассмотрим цепь с тремя резисторами
Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока. Но вот что будет с напряжением на каждом резисторе и как его найти?
Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на любом резисторе. Давайте так и сделаем.
Пусть у нас будет цепь с такими параметрами.
Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.
Получается, что в данном случае RAB =R1 + R2 + R3 = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.
Половина дела сделано. Теперь осталось узнать, какое напряжение падает на каждом резисторе. То есть нам надо найти значения UR1 , UR2 , UR3 . Но как это сделать?
Да все также, через закон Ома. Мы знаем, что через каждый резистор проходит сила тока 1 Ампер, мы уже вычислили это значение. Закон ома гласит I=U/R , отсюда получаем, что U=IR.
Следовательно,
UR1 = IR1 =1×2=2 Вольта
UR2 = IR2 = 1×3=3 Вольта
UR3 = IR3 =1×5=5 Вольт
Теперь начинается самое интересное. Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.
Получается
U=UR1+UR2+UR3
Мы получили самый простой делитель напряжения.
Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.
Основные законы
Проектирование электрических цепей предполагает наличие хороших знаний основных закономерностей последовательного и параллельного подключения нагрузки. Это касается не только закона Ома, но и постулатов Кирхгофа. Эти физики внесли большой вклад в развитие электротехники. Для более простого восприятия основных законов все формулы стоит рассматривать в следующей последовательности:
- при последовательном соединении через каждый участок цепи протекает ток одинаковой силы;
- общее сопротивление схемы при последовательном подключении равно сумме сопротивления всех проводников;
- напряжение в электросети при параллельном подключении одинаково для каждого участка;
Для последовательного соединения нагрузок применим второй закон Кирхгофа. Согласно ему, сумма ЭДС в замкнутом электрическом контуре равна сумме падений напряжений на каждой нагрузке. В результате общее сопротивление можно определить с помощью следующей формулы: Ro = R1 + R2.
Также можно рассчитать и индуктивность при различных видах соединения катушек. В случае с последовательным все довольно просто, достаточно использовать следующую формулу: Lo = L1 + L2. По сути, вместо двух элементов можно установить один с соответствующим показателем индуктивности.
При параллельном подсоединении катушек ситуация усложняется, так как возможны три варианта:
- магнитные поля катушек не пересекаются: Lo = L1 * L2 / L1 + L2;
- катушки подсоединены в одном направлении и их поля пересекаются: Lo = L1 * L2-М2 / L1 + L2 — 2 М;
- пересечение полей наблюдается при встречном подсоединении: Lo = L1 * L2-М2 / L1 + L2 + 2 М.
Последовательное соединение
Последовательным называется соединение двух и более резисторов, при котором конец первого элемента соединяется с началом второго и так далее. В результате получается последовательная цепочка, где по всем ее составляющим проходит одинаковый ток. В качестве примера можно взять последовательную цепь, состоящую из трех резисторов R1, R2 и R3. Сопротивление в источнике тока принимается с нулевым значением. В соответствии со вторым законом Кирхгофа получается следующая формула: E = IR1 + IR2 + IR3 = I(R1 + R2 + R3) = IRэк.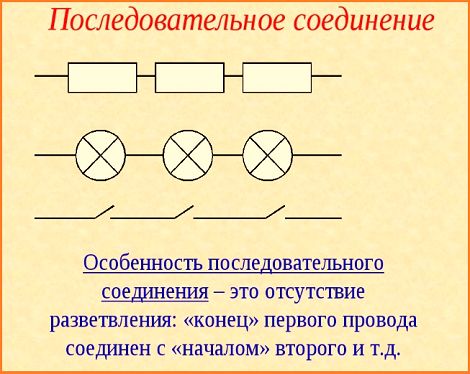
В этой формуле значение эквивалентного сопротивления последовательной цепи составит сумму сопротивлений всех резисторов, имеющихся в данной цепи: Rэк = R1 + R2 + R3. По закону Ома напряжение при последовательном соединении на отдельных участках будет иметь следующее значение, поскольку E = U: U1=IR1; U2 = IR2, U3 = IRз, то есть U = U1 + U2 +U3. Данные формулы показывают, что в резисторах, последовательно соединенных между собой, напряжения распределяются пропорционально их сопротивлениям. То есть, чем выше сопротивление любого из резисторов, тем больше напряжение, приложенное к нему. В виде формулы — это утверждение будет выглядеть следующим образом: U1 : U2 : U3 = R1 : R2 : R3.
При последовательном соединении сопротивление R1 нескольких резисторов в количестве n, будет одинаковым. Следовательно, значение эквивалентного сопротивления цепи будет в n раз превышать сопротивление каждого из них: Rэк = nR1. Следовательно напряжение на каждом отдельном резисторе будет в n раз меньше, чем общее напряжение цепи: U1 = U/n.
Таким образом, изменение сопротивления любого из резисторов при последовательном соединении, приводит к изменению напряжения на других резисторах, находящихся с ним в одной цепи. Поэтому, если электрическая цепь обрывается или выключается в одной из нагрузок, в других нагрузках также прекращается течение тока. Из-за этого последовательное соединение в электрических схемах используется довольно редко.
Параллельное соединение сопротивлений
При параллельном подключении все сопротивления подключаются началами к одной точке источника питания, а концами к другой. Далеко ходить не будем, и посмотрим вокруг себя. Фен, утюг, стиральная машинка, тостер, микроволновка и любой другой электрический прибор имеют вилку с двумя рабочими концами и одним защитным (заземлением). Напряжение в розетке это наш источник питания. Сколько бы электроприборов мы не включили в сеть – мы их все включаем параллельно к одному источнику питания. Давайте нарисуем схему, чтобы стало более понятно.
Сколько бы эту схему не добавилось потребителей – ровным счётом ничего не меняется. Один конец электроприбора подключается к нулевой шине, а второй к фазе. Теперь несколько преобразуем схему:
Теперь перед нами три сопротивления:
Утюг 2,2 кВт – R1 (22 Ом);
Плита 3,5 кВт – R2 (14 Ом);
Лампочка 100 Вт – R3 (484 Ом).
Таковы реальные значения сопротивления этих потребителей электрическому току. Включаем по очереди наши потребители в сеть, и что происходит со счетчиком? Правильно, он начинает быстрее считать деньги в нашем кошельке. Теперь вспоминаем закон Ома, который гласит, что сила тока обратно пропорциональна сопротивлению и понимаем, что чем меньше сопротивление, тем выше сила тока. А чтобы еще проще было понять, что происходит, представьте себе концертный зал с тремя разными по габаритам выходами и толпой людей. Чем больше по габаритам открывается дверь, тем больше человек одновременно могут через нее пройти, а чем больше откроется дверей, тем больше это увеличит пропускную способность. Ну а теперь перейдём к формулам.
К каждому сопротивлению приложено одно и то же напряжение – 220 вольт.
Из схемы и из практики видим, что токи складываются в один общий, следовательно, получаем следующее уравнение:
Если внимательно присмотритесь к уравнению, то заметите, что верхняя часть уравнения у нас неизменна и её можно принять за единицу, получив следующую формулу:
Ещё есть частная формула для расчёта двух параллельно соединенных сопротивлений:
Ну и давайте на практике сделаем расчёт.
И получим общее сопротивление 8,407 Ом.
В предыдущей статье я рассматривал баланс мощности и давайте его проверим.
Мощность цепи будет:
Считаем наши мощности: 2000+3500+100=5600, что почти равно 5757, такая большая погрешность обусловлена тем, что я округлил значения сопротивлений до целых чисел.
Какие можно сделать выводы. Как видите, общее сопротивление (его ещё называют эквивалентным) всегда будет меньше, чем самое малое сопротивление цепи. В нашем случае это плита с сопротивлением 14 Ом и эквивалентное 8,4 Ом. Оно и понятно. Помните пример с дверями в концертном зале? Сопротивление можно назвать пропускной способностью. Так вот общее количество выходящих людей (электронов) из зала будет в сумме больше, чем пропускная способность каждой отдельно взятой двери. То есть, количество тока увеличивается. Другими словами, для тока каждое из сопротивлений будет еще одной дверью, через которые он может протекать.
Последовательное соединение сопротивлений
При последовательном соединении конец одного сопротивления соединяется с другим. Типовой пример такого соединения – новогодняя гирлянда.
Насколько известно из школьного курса физики по замкнутому контуру протекает только один ток. Таким образом, что мы имеем:
Лампочка 200 ватт – R1 (242 Ом)
Лампочка 100 ватт – R2 (484 Ом)
Лампочка 50 ватт – R3 (968 Ом)
Снова вернёмся к аллегории и представим концертный зал, но только в этот раз из него будет вести длинный коридор с тремя дверями. Теперь у тока (людей) только один путь последовательно пройти от одной двери к другой. Для решения этой задачи нам придется отталкиваться от напряжения. Исходя из того, что сумма на источнике питания равна сумме падений напряжений на сопротивлениях получим следующую формулу:
Отсюда следует:
Делим обе части уравнения на общую величину приходим к выводу, что при последовательном соединении для получения эквивалентного сопротивления цепи надо суммировать все сопротивления этой цепи:
Проверяем. R=242+484+968=1694 Ом
Как видим, баланс мощности почти сошёлся
А теперь внимание на одну особенность, которая ещё раз раскроет понятие «сопротивление». Обратите внимание, что наибольшая мощность у нас будет на самой слабой лампочке:
Казалось бы, должно быть все наоборот, более мощная лампочка должна светить ярче. Возвращаемся к нашей аллегории. Как вы думаете, где будет давка сильнее возле широкой двери или возле узкой? Где будет горячее? Конечно же, возле узкой двери возникнет давка, а там где давка, там будет горячо, потому что люди будут стараться проложить себе путь побыстрее. В токе роль людей выполняют электроны. Вот такой вот парадокс возникает при включении в последовательную цепь резисторов разного номинала и именно поэтому в гирляндах стараются применять одинаковые лампочки. Теперь, зная принципы последовательного соединения сопротивлений, вы можете рассчитать любую гирлянду. Например, у вас имеются автомобильные лампы на 12 вольт. Зная, что общее напряжение равно сумме падений напряжений нам достаточно 220 вольт разделить на 12 вольт и получим 18,3 лампы. То есть, если взять 18 или 19 одинаковых 12 вольтовых ламп и соединить последовательно, то их можно включить в 220 вольт и они не перегорят.
Подведём итоги
При параллельном соединении сопротивлений эквивалентное сопротивление уменьшается (концертный зал опустошается в три раза быстрее, грубо говоря, люди разбегаются по трем коридорам), а при последовательном соединении сопротивление увеличивается (как бы люди не хотели быстрее покинуть зал, делать им это придется только по одному коридору и чем коридор уже, тем больше сопротивление он создает).
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
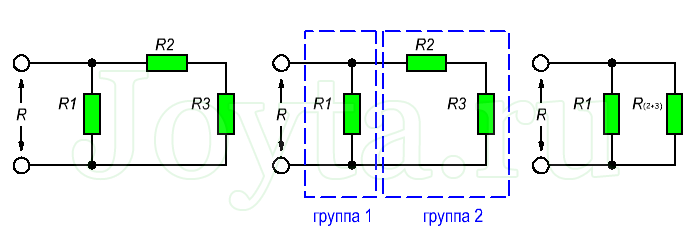
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
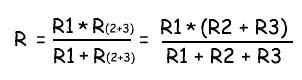
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Пример расчёта
Для большей наглядности можно рассмотреть следующий пример: допустим, у нас есть три резистора, чьи номиналы соответственно равны 100, 150 и 30 Ом. Если воспользоваться первой формулой для определения общего номинала, то получим следующее:
R(общ)=1/(1/100+1/150+1/30)=
1/(0,01+0,007+0,03)=1/0,047=21,28Ом.
Если выполнить несложные расчеты, то можно получить следующее: для цепи, включающей в себя три детали, где наименьший показатель сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального значения номинала в цепи практически на 30%.
Последовательное соединение проводников
Сопротивление при последовательном соединении проводников
Последовательное соединение проводников – это когда к одному проводнику мы соединяем другой проводник и так по цепочке. Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.
последовательное соединение резисторов
Чему же будет равняться их общее сопротивление? Оказывается, все просто. Оно будет равняться сумме всех сопротивлений проводников в этой цепи.
Получается, можно записать, что
формула при последовательном соединении резисторов
Пример
У нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.
Решение
Rобщее =R1 + R2 + R3 = 3+5+2=10 Ом.
То есть, как вы видите, цепочку из 3 резисторов мы просто заменили на один резистор RAB .
показать на реальном примере с помощью мультиметра
Видео где подробно расписывается про эти соединения:
https://youtube.com/watch?v=0hFWeR8ybxs
Сила тока через последовательное соединение проводников
Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома I=U/R.
Получается, если через резистор RAB течет какой-то определенный ток, следовательно, если разложить наш резистор на составляющие R1 , R2 , R3 , то получится, что через них течет та же самая сила тока, которая текла через резистор RAB .
сила тока через последовательное соединение проводников
Получается, что при последовательном соединении проводников сила тока, которая течет через каждый проводник одинакова. То есть через резистор R1 течет такая же сила тока, как и через резистор R2 и такая же сила тока течет через резистор R3 .
Напряжение при последовательном соединении проводников
Давайте еще раз рассмотрим цепь с тремя резисторами
Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока. Но вот что будет с напряжением на каждом резисторе и как его найти?
Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на любом резисторе. Давайте так и сделаем.
Пусть у нас будет цепь с такими параметрами.
Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.
Получается, что в данном случае RAB =R1 + R2 + R3 = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.
Половина дела сделано. Теперь осталось узнать, какое напряжение падает на каждом резисторе. То есть нам надо найти значения UR1 , UR2 , UR3 . Но как это сделать?
Да все также, через закон Ома. Мы знаем, что через каждый резистор проходит сила тока 1 Ампер, мы уже вычислили это значение. Закон ома гласит I=U/R , отсюда получаем, что U=IR.
Следовательно,
UR1 = IR1 =1×2=2 Вольта
UR2 = IR2 = 1×3=3 Вольта
UR3 = IR3 =1×5=5 Вольт
Теперь начинается самое интересное. Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.
Получается
U=UR1+UR2+UR3
Мы получили самый простой делитель напряжения.
Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.
