Магнитный поток

Причины возникновения индукционного тока в движущихся и неподвижных проводниках

Причин, по которым может происходить изменение магнитного потока, пронизывающего замкнутый контур, две:

1. Изменение магнитного потока вследствие перемещения всего контура или отдельных его частей в магнитном поле, которое не изменяется со временем;
2. Изменение магнитного поля при неподвижном контуре.

Перейдем к рассмотрению этих случаев подробнее.

Перемещение контура или его частей в неизменном магнитном поле

При движении проводников и свободных носителей заряда в магнитном поле возникает ЭДС индукции. Объяснить возникновение δинд можно действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца здесь – это сторонняя сила.

Пример 2

На рисунке мы изобразили пример индукции, когда прямоугольный контур помещен в однородное магнитное поле B→ направленное перпендикулярно плоскости контура. Одна из сторон контура перемещается по двум другим сторонам с некоторой скоростью.

Рисунок 1.20.3. Возникновение ЭДС индукции в движущемся проводнике. Отражена составляющая силы Лоренца, которая действует на свободный электрон

На свободные заряды подвижной части контура воздействует сила Лоренца. Основная составляющая силы Лоренца в данном случае направлена вдоль проводника и связана с переносной скоростью зарядов υ→. Модуль этой сторонней силы равен:

FЛ=eυ→B.

Работа силы FЛ на пути l равна:

A=FЛ·l=eυBl.

По определению ЭДС: 

δинд=Ae=υBl.

Значение сторонней силы для неподвижных частей контура равно нулю. Для соотношения δинд можно записать другой вариант формулы. Площадь контура с течением времени изменяется на ΔS=lυΔt. Соответственно, магнитный поток тоже будет с течением времени изменяться: ΔΦ=BlυΔt.

Следовательно, 

δинд=∆Φ∆t.

Знаки в формуле, которая связывает δинд и ∆Φ∆t, можно установить в зависимости от того, какие направления нормали и направления контура будут выбраны. В случае выбора согласованных между собой по правилу правого буравчика направлений нормали n→ и положительного направления обхода контура l→ можно прийти к формуле Фарадея.

При условии, что сопротивление всей цепи – это R, то по ней будет протекать индукционный ток, который равен Iинд=δиндR. За время Δt на сопротивлении R выделится джоулево тепло:

∆Q=RIинд2∆t=υ2B2l2R∆t

Парадокса здесь нет. Мы просто не учли воздействие на систему еще одной силы. Объяснение заключается в том, что при протекании индукционного тока по проводнику, расположенному в магнитном поле, на свободные заряды действует еще одна составляющая силы Лоренца, которая связана с относительной скоростью движения зарядов вдоль проводника. Благодаря этой составляющей появляется сила Ампера FА→.

Для рассмотренного выше примера модуль силы Ампера равен FA =IBl. Направление силы Ампера таково, что она совершает отрицательную механическую работу Aмех. Вычислить эту механическую работу за определенный период времени можно по формуле:

Aмех=-Fυ∆t=-IBlυ∆t=-υ2B2l2R∆t

Проводник, перемещающийся в магнитном поле, испытывает магнитное торможение. Это приводит к тому, что полная работа силы Лоренца равна нулю. Джоулево тепло может выделяться либо за счет уменьшения кинетической энергии движущегося проводника, либо за счет энергии, которая поддерживает скорость перемещения проводника в пространстве.

Изменение магнитного поля при неподвижном контуре

Определение 3

Вихревое электрическое поле – это электрическое поле, которое вызывается изменяющимся магнитным полем.

В отличие от потенциального электрического поля работа вихревого электрического поля при перемещении единичного положительного заряда по замкнутому проводящему контуру равна δинд в неподвижном проводнике.

В неподвижном проводнике электроны могут приводиться в движение только под действием электрического поля. А возникновение δинд нельзя объяснить действием силы Лоренца.

Первым, кто ввел понятие вихревого электрического поля, был английский физик Джон Максвелл. Случилось это в 1861 году.

Фактически, явления индукции в подвижных и неподвижных проводниках протекают одинаково. Так что в этом случае мы тоже можем использовать формулу Фарадея. Отличия касаются физической причины возникновения индукционного тока: в движущихся проводниках δинд обусловлена силой Лоренца, в неподвижных – действием на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Рисунок 1.20.4. Модель электромагнитной индукции

Рисунок 1.20.5. Модель опытов Фарадея

Рисунок 1.20.6. Модель генератора переменного тока

Всё ещё сложно?
Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

Закон электромагнитной индукции

Закон электромагнитной индукции (закон Фарадея) звучит так:

ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром.

Математически его можно описать формулой:

Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре всегда направлен так, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.

Если контур состоит из ​N витков (то есть он — катушка), то ЭДС индукции будет вычисляться следующим образом.

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ​R​:

Если проводник длиной l будет двигаться со скоростью ​v​ в постоянном однородном магнитном поле с индукцией ​B​ ЭДС электромагнитной индукции равна:

Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.

Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:

• вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле
• вследствие изменения во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея

Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:

• в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца
• в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Постоянные магниты

Источником магнитного поля (МП) могут служить постоянные магниты. Они изготавливаются из магнетита. В природе он известен как оксид железа. Это минерал чёрной окраски, имеющий молекулярное строение FeO·Fe2O3. Свойства магнитов известны с давних времён. Магниты имеют два полюса – северный и южный.

Постоянные магниты можно классифицировать по следующим критериям:

• материал, из которого изготовлен магнит;
• форма;
• сфера использования.

Магниты с постоянными полюсами изготавливаются из различных материалов:

• ферритов – прессованных изделий из порошков оксида железа и оксидов иных металлов;
• редкоземельных – нодимовых (NdFeB), самариевых (SmCo), литых (сплавы металлов), полимерных (магнитопласты).

Форма магнитов самая различная:

• цилиндрическая (прямоугольная);
• подковообразная;
• кольцеобразная;
• дискообразная.

Направление линий МП в зависимости от формы магнита

Постоянные магниты нашли широкое применение в различных отраслях народного хозяйства:

• МРТ – медицинский прибор для диагностики человеческого организма;
• приводы жёстких дисков в современных компьютерах;
• в радиотехнике, при изготовлении динамиков;
• производство декоративных украшений с применением магнитов на полимерной основе.

В двигателях постоянного тока такие магниты вмонтированы в корпус индуктора.

Магнитное поле проводника с током

Оказывается, если через какой-либо проводник пропустить электрический ток, то вокруг проводника образуется магнитное поле.

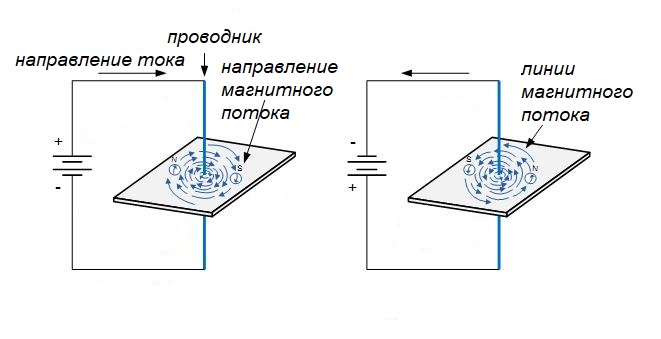
Здесь можно вспомнить знаменитое правило буравчика, но для наглядности я лучше буду использовать правило самореза, так как почти все хоть раз в жизни ввинчивали либо болт, либо саморез.

Ввинчиваем по часовой стрелке – саморез идет вниз. В нашем случае он показывает направление электрического тока. Движение наших рук показывает направление линий магнитного поля. Все то же самое, когда мы начинаем откручивать саморез. Он начинает вылазить вверх, то есть в нашем случае показывает направление электрического тока, а наша рука в этом время рисует в воздухе направление линий магнитного поля.

Также часто в учебниках физики можно увидеть, что направление электрического тока от нас рисуют кружочком с крестиком, а к нам – кружочком с точкой. В этом случае опять представляем себе саморез и уже в голове увидим направление магнитного поля.

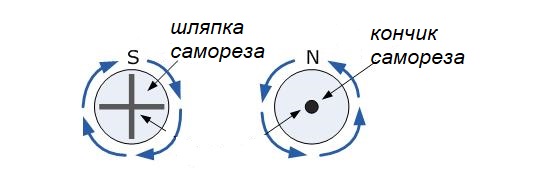
Как думаете, что будет если мы сделаем вот такую петельку из провода? Что изменится в этом случае?

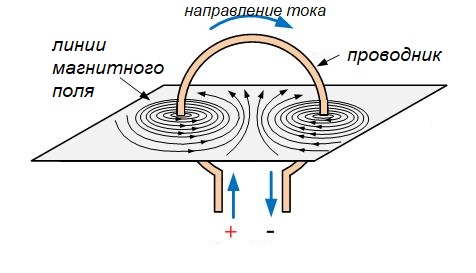
Давайте же рассмотрим этот случай более подробно. Так в этой плоскости оба проводника создают магнитное поле, то по идее они должны отталкиваться друг от друга. Но если они хорошо закреплены, то начинается самое интересное. Давайте рассмотрим вид сверху, как это выглядит.

Как вы можете заметить, в области, где суммируются магнитные силовые линии плотность магнитного потока прям зашкаливает.

Взаимодействие магнита с контуром

В качестве наглядного примера взаимодействия магнита и контура в сделанную из медного провода катушку помещают магнит. Если магнит медленно вставлять внутрь катушки, происходит постепенное увеличение пересекающего ее витки создаваемого магнитом потока. Появляющееся вследствие такой манипуляции упорядоченное движение частиц в катушке будет направлено по часовой стрелке, создавая собственное магнитное поле, ослабляющее поле магнита, отталкивая его тем самым от катушки.

Если магнит отдаляют от контура, его поток уменьшается, а заряженные частицы начинают двигаться против часовой стрелки, вследствие чего возникающая совокупность силовых магнитных линий будет притягивать магнит.

На заметку. В случае с незамкнутым (открытым) контуром: металлическим или алюминиевым кольцом, имеющим прорезь; катушкой, витки которой не замкнуты через амперметр, источник питания, данная закономерность, как и правило Ленца, не работает.

Основные уравнения

Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в огромное множество уравнений, иногда непосредственно, иногда через связанную с ним напряжённость магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, это пожалуй разве только чистая электростатика.

(Здесь формулы приведем в СИ, в виде для вакуума, где есть варианты для вакуума — для среды; запись в другом виде и подробности — см. по ссылкам).

В магнитостатике

В магнитостатическом пределе наиболее важными являются:

• Закон Био — Савара — Лапласа: играет в магнитостатике ту же роль, что закон Кулона в электростатике:

  B→(r→)=μ4π∫L1I(r→1)dL1→×(r→−r→1)|r→−r→1|3,{\displaystyle {\vec {B}}\left({\vec {r}}\right)={\mu _{0} \over 4\pi }\int \limits _{L_{1}}{\frac {I\left({\vec {r}}_{1}\right){\vec {dL_{1}}}\times \left({\vec {r}}-{\vec {r}}_{1}\right)}{\left|{\vec {r}}-{\vec {r}}_{1}\right|^{3}}},}

  B→(r→)=μ4π∫j→(r→1)dV1×(r→−r→1)|r→−r→1|3,{\displaystyle {\vec {B}}\left({\vec {r}}\right)={\mu _{0} \over 4\pi }\int {\frac {{\vec {j}}\left({\vec {r}}_{1}\right)dV_{1}\times \left({\vec {r}}-{\vec {r}}_{1}\right)}{\left|{\vec {r}}-{\vec {r}}_{1}\right|^{3}}},}

• Теорема Ампера о циркуляции магнитного поля:

  ∮∂S⁡B→⋅dl→=μIS≡μ∫Sj→⋅dS→,{\displaystyle \oint \limits _{\partial S}{\vec {B}}\cdot {\vec {dl}}=\mu _{0}I_{S}\equiv \mu _{0}\int \limits _{S}{\vec {j}}\cdot {\vec {dS}},}

  rotB→≡∇→×B→=μj→.{\displaystyle \mathrm {rot} \,{\vec {B}}\equiv {\vec {\nabla }}\times {\vec {B}}=\mu _{0}{\vec {j}}.}

В общем случае

Основные уравнения (классической) электродинамики общего случая (то есть независимо от ограничений магнитостатики), в которых участвует вектор магнитной индукции B→{\displaystyle {\vec {B}}}:

Три из четырех уравнений Максвелла (основных уравнений электродинамики)

divE→=ρε,   rotE→=−∂B→∂t{\displaystyle \mathrm {div} \,{\vec {E}}={\frac {\rho }{\varepsilon _{0}}},\ \ \ \mathrm {rot} \,{\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}}}

divB→=,    rotB→=μj→+1c2∂E→∂t{\displaystyle \mathrm {div} \,{\vec {B}}=0,\ \ \ \ \,\mathrm {rot} \,{\vec {B}}=\mu _{0}{\vec {j}}+{\frac {1}{c^{2}}}{\frac {\partial {\vec {E}}}{\partial t}}}

а именно:

Закон отсутствия монополя:

divB→=,{\displaystyle \mathrm {div} \,{\vec {B}}=0,}

Закон электромагнитной индукции Фарадея:

rotE→=−∂B→∂t,{\displaystyle \mathrm {rot} \,{\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}},}

Закон Ампера — Максвелла:

rotB→=μj→+1c2∂E→∂t.{\displaystyle \mathrm {rot} \,{\vec {B}}=\mu _{0}{\vec {j}}+{\frac {1}{c^{2}}}{\frac {\partial {\vec {E}}}{\partial t}}.}

Формула силы Лоренца:

F→=qE→+qv→×B→,{\displaystyle {\vec {F}}=q{\vec {E}}+q\left,}

Следствия из неё, такие как

Выражение для силы Ампера, действующей со стороны магнитного поля на ток (участок провода с током)

dF→=Idl→×B→,{\displaystyle d{\vec {F}}=\left,}

dF→=j→dV×B→,{\displaystyle d{\vec {F}}=\left,}

выражение для момента силы, действующего со стороны магнитного поля на магнитный диполь (виток с током, катушку или постоянный магнит):

M→=m→×B→,{\displaystyle {\vec {M}}={\vec {m}}\times {\vec {B}},}

выражение для потенциальной энергии магнитного диполя в магнитном поле:

U=−m→⋅B→,{\displaystyle U=-{\vec {m}}\cdot {\vec {B}},}

• а также следующих из них выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле и т. д..
• Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:

F→=Kqmr→r3.{\displaystyle {\vec {F}}=K{\frac {q_{m}{\vec {r}}}{r^{3}}}.}

(это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).

Выражение для плотности энергии магнитного поля

w=B22μ{\displaystyle w={\frac {B^{2}}{2\mu _{0}}}}

Оно в свою очередь входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля и в лагранжиан электромагнитного поля и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).

Магнитное поле снаружи прямолинейного тока.

Магнитное поле прямолинейного тока

наблюдают, продев сквозь расположенный горизонтально лист картона вертикальный прямолинейный провод, представляющий собой часть электрической цепи. Опилки-стрелочки при замыкании тока в цепи и после легкого постукивания по листу образуют цепочки в виде окружностей с общим центром на оси тока. Поэтому магнитное поле электрического тока графически изображают в виде линий магнитной индукции, аналогичных линиям напряженности электростатического поля. Линии магнитной индукции представляют собой окружности с центрами на оси тока, расположенные в плоскостях, перпендикулярных направлению тока. Их направление определяют по правилу правого винта: при поступательном движении винта в направлении тока его вращение указывает направление магнитного поля этого тока. Различие между линиями магнитной индукции и линиями напряженности электростатического поля: первые замкнуты и окружают электрический ток; вторые – разомкнуты, начинаются на поверхности положительно заряженных тел и оканчиваются на поверхности отрицательно заряженных.

Магнитосфера Земли

Магнитосферой называется пространство, прилежащее к небесному телу и обладающее особыми свойствами, которые определяются взаимодействием МП планеты с заряженными частицами из внешнего пространства. Для Земли диаметр этой сферы составляет более 90 тысяч километров.

Наша планета обладает основным и переменным магнитными полями. Первое формируется электротоками, образующимися на плотном ядре вследствие разницы температур. Второе образуется из-за действия внешних сил (электротоков в атмосфере) и отличается большой нестабильностью. С ним связаны такие явления, как магнитные бури и северное сияние.

Полевое пространство Земли может быть описано рядом показателей, например, его напряженность описывает силу и привязана к географической широте. Магнитное склонение показывает разницу между меридианом (с вектором, направленным на север) и соответствующей позицией магнитной стрелки.

Конвертер величин

Калькуляторы

В этой части Конвертера физических единиц TranslatorsCafe.com представлена группа калькуляторов, выполняющих расчеты в различных областях электротехники, радиотехники и электроники.

Магнитостатика, магнетизм и электродинамика

Магнитостатика — раздел классической электродинамики, изучающий взаимодействие постоянных токов посредством создаваемого ими постоянного магнитного поля и способы расчета магнитного поля в этом случае.

Электродинамика

— раздел физики, изучающий силы, возникающие при взаимодействии электрически заряженных частиц и тел. Эти силы объясняются в электродинамике с помощью электромагнитных полей. Силы электромагнитного взаимодействия лежат в основе большинства явлений, с которыми мы встречаемся в повседневной жизни. Часть привычных явлений обусловлена действием гравитационных сил.

Электромагнитное поле

— физическое поле, появляющееся при взаимодействии движущихся заряженных телами или частиц. Электромагнитное поле можно рассматривать как сочетание электрического и магнитного полей.

Электрическое поле

— физическое поле, окружающее электрически заряженные частицы, проводники с проходящими в них электрическими токами и изменяющиеся во времени и пространстве магнитные поля.

Магнитное поле

— физическое силовое поле, окружающее заряженные частицы, проводники с электрическим током, магнитные материалы и переменные электрические поля, а также действующее на проводники с электрическим током, движущиеся электрические заряды и тела, обладающие магнитным моментом. Магнитное поле в любой точке определяется направлением и силой и таким образом является векторным полем. Магнитное поле характеризуется двумя основными величинам — вектором магнитной индукцииВ и вектором напряженности магнитного поляH .

Конвертер магнитного потока

Магнитный поток

определяется как интеграл вектора магнитной индукции через конечную поверхность. Также магнитный поток можно рассчитать как скалярное произведение вектора магнитной индукции на вектор площади. Для измерения магнитного потока используют флюксметр, который измеряет напряжение на измерительной катушке.

В СИ единицей магнитного потока является вебер

(Вб, размерность — В·с = кг·м²·с⁻²·А⁻¹). Магнитный поток, равный 1 Вб, создается магнитным полем с индукцией 1 Тл, пронизывающим по направлению нормали плоский контур площадью 1 м². В системе СГС — магнитный поток измеряется вмаксвеллах (Мкс).

Использование конвертера «Конвертер магнитного потока»

На этих страницах размещены конвертеры единиц измерения, позволяющие быстро и точно перевести значения из одних единиц в другие, а также из одной системы единиц в другую. Конвертеры пригодятся инженерам, переводчикам и всем, кто работает с разными единицами измерения.

Изучайте технический английский язык и технический русский язык с нашими видео! — Learn technical English and technical Russian with our videos!

Пользуйтесь конвертером для преобразования нескольких сотен единиц в 76 категориях или несколько тысяч пар единиц, включая метрические, британские и американские единицы. Вы сможете перевести единицы измерения длины, площади, объема, ускорения, силы, массы, потока, плотности, удельного объема, мощности, давления, напряжения, температуры, времени, момента, скорости, вязкости, электромагнитные и другие. Примечание.

В связи с ограниченной точностью преобразования возможны ошибки округления. В этом конвертере целые числа считаются точными до 15 знаков, а максимальное количество цифр после десятичной запятой или точки равно 10.

Для представления очень больших и очень малых чисел в этом калькуляторе используется компьютерная экспоненциальная запись

, являющаяся альтернативной формой нормализованной экспоненциальной (научной) записи, в которой числа записываются в форме a · 10x. Например: 1 103 000 = 1,103 · 106 = 1,103E+6. Здесь E (сокращение отexponent ) — означает «· 10^», то есть«…умножить на десять в степени…» . Компьютерная экспоненциальная запись широко используется в научных, математических и инженерных расчетах.

Мы работаем над обеспечением точности конвертеров и калькуляторов TranslatorsCafe.com, однако мы не можем гарантировать, что они не содержат ошибок и неточностей. Вся информация предоставляется «как есть», без каких-либо гарантий. Условия.

Если вы заметили неточность в расчётах или ошибку в тексте, или вам необходим другой конвертер для перевода из одной единицы измерения в другую, которого нет на нашем сайте — напишите нам!

Канал Конвертера единиц TranslatorsCafe.com на YouTube

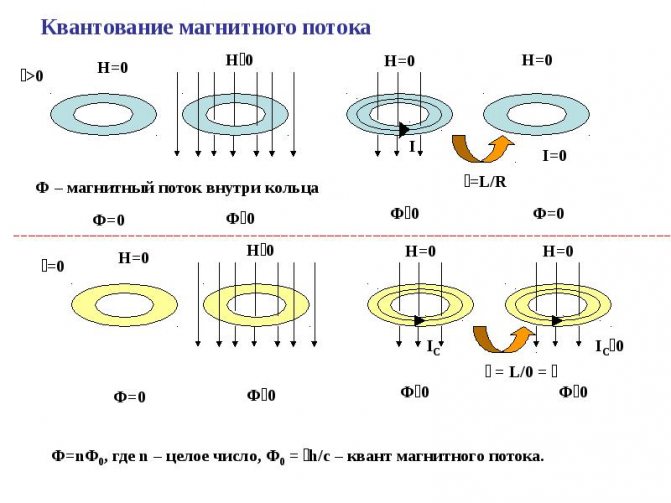
Квантование магнитного потока

В 1961 году практически было установлено, что, если направить магнитный поток через закольцованный сверхпроводник, по которому протекает электричество, то величина Φ будет кратной кванту потока Φ0 = h/2e = 2.067833758*10-15Вб. Это значение в системе СИ.

Сопротивление тока: формула

Такой эксперимент выполнили американцы Дивер и Фейрбенк. Они выполнили квантование, используя трубку полой конструкции, пропуская по ней круговые токи сверхпроводящей природы. Их результат квантовой размерности оказался в два раза меньше. Это было обусловлено тем, что электроны в сверхпроводящей ситуации разбивались на пары. Частицы образовывали двойки с зарядом 2е. Именно движение этих пар составляет природу сверхпроводящего тока.

К сведению. Сверхпроводники – это материалы, у которых при понижении температуры до определённого значения резко падает сопротивление. Оно практически равно нулю, тогда можно говорить о сверхпроводящих свойствах. Металлы, которые являются отличными проводниками, – золото, серебро, платина, не приобретают сверхпроводящих способностей в таких условиях.

Квантование магнитного потока

Похожие записи:

Распиновка цоколя лампы h4. led лампы autoleader h4 в фары Обзор makita 5704r Установка столба на дачном участке. установка столбов под электричество Топ-7 лучших терморегуляторов: какой выбрать, для теплого пола, с датчиком, отзывы, цена Автоматическое включение фар при запуске двигателя автомобиля своими руками Топ новых гаджетов 2020 года