Поиск ответа
| Вопрос № 301473 |
Ответ справочной службы русского языка
Ответ справочной службы русского языка
Ответ справочной службы русского языка
Ответ справочной службы русского языка
О создании ППЭ и назначение ответственного руководителя ППЭ
В целях обеспечения эффективной подготовки к Единому государственному экзамену в 2008/2009 учебном году Приказываю:
1. Создать Пункт проведения экзамена (ППЭ) по адресу: г. Москва, ул., д., Количество аудиторий – 4. Вместимость – 60 человек. 2. Назначить руководителем Пункта проведения экзамена (ППЭ) методиста Иванову И.Ю. Контактный телефон: 3. Назначить организаторов в аудитории: преподавателя Петрову А.И., зав.отделения по воспитательной работе Капитанову Е.Н., преподавателя Звенигородскую Н.С., педагога-организатора Можарову О.А. 4. Назначить дежурных по этажу: зав. отделения Серпецкую С.В., библиотекаря Кригер В.П., старшего мастера Касаткину В.К. 5. Назначить дежурных на регистрации: мастера п/о Илюхину Н.А, мастера п/о Возвышаеву Е.В., мастера п/о Антонову Л.В. 6. Назначить оператором ПЭВМ мастера п/о Пряхину Е.А. 7. Ответственность за исполнение настоящего приказа возложить на методиста Сурову И.Ю. Директор Соколова И.О. хотелось бы узнать правильно ли я написала окончания при таком сотавлении приказа.
Ответ справочной службы русского языка
В названии приказа должно быть: О создании ППЭ и назначени и .
Обратите внимание: слово заведующий управляет творительным падежом. Правильно: зав
отделени ем .
Ответ справочной службы русского языка
Ответ справочной службы русского языка
Ответ справочной службы русского языка
Ответ справочной службы русского языка
Ответ справочной службы русского языка
Ответ справочной службы русского языка
Ответ справочной службы русского языка
Источник статьи: http://new.gramota.ru/spravka/buro/search-answer?s=%D0%B2%D0%BC%D0%B5%D1%81%D1%82%D0%B8%D0%BC%D0%BE%D1%81%D1%82%D1%8C
Свойства
Емкость
. Это основное свойство конденсатора. Измеряется в Фарадах и вычисляется по следующей формуле (для плоского конденсатора):
где С, q, U — это соответственно емкость, заряд, напряжение между обкладками, S –площадь обкладок, d – расстояние между ними, — диэлектрическая проницаемость, — диэлектрическая постоянная, равная 8,854*10^-12 Ф/м..
Полярность конденсатора
Номинальное напряжение
Удельная емкость и другие
Величина емкости конденсатора зависит от
Площадь пластин
. Это понятно из формулы: емкость прямо пропорциональна заряду. Естественно, увеличив площадь обкладок, получаем большее количество заряда.
Расстояния между обкладками
. Чем они ближе расположены, тем больше напряженность получаемого электрического поля.
Значение слова «ёмкость»

1. Способность вместить в себя определенное количество чего-л.; вместимость. Емкость сосуда. □ Дом поразил его своей удивительной емкостью. 466 Он был так тесно набит людьми, что казалось — людей в нем больше, чем во всей деревне Китежной. М. Горький, Трое.
2. мн. ч. (ёмкости, –ей). Спец. Сосуды для хранения чего-л. Емкости с горючим.
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
Ёмкость — многозначное слово, может означать:
Ёмкость — внутренний объём сосуда, вместимость, то есть максимальный объём помещающейся внутрь него чего либо.
Ёмкость — сосуд, контейнер или резервуар для хранения или транспортирования жидкостей, газов, сыпучих тел и другого.
ЁМКОСТЬ, и, мн. нет, ж. (книжн.). Внутренний объем, способность вместить определенное количество содержимого. Е. винной бутылки равняется 0,7 литра. || Способность вместить, разместить в себе. Е. рынка. ◊
ёмкость
1. свойство по значению прилагательного ёмкий; способность вмещать что-либо; вместимость ◆ Галеран хотел ещё измерить ёмкость сарая, пустых ящиков и бочек, загромождавших маленький двор лавки. Грин, «Дорога никуда», 1929 г. (цитата из НКРЯ) ◆ Надо только уметь учить, а ёмкость мозга такова, что она вместит невероятное количество знаний. Ефремов, «Лезвие бритвы», 1959–1963 г.
2. перен. сосуд, вместилище для жидких и сыпучих тел
3. физ. техн. электрическая характеристика, способность накапливать заряд
4. техн. разг. то же, что конденсатор
5. техн. характеристика химического источника тока, количество электричества, которое может быть отдано в электрическую цепь ◆ Изобретение уплотнения электричества, приведшее к созданию аккумуляторов огромной ёмкости и компактных, но мощных электромоторов, было крупнейшей технической революцией нового времени. Ефремов, «Туманность Андромеды», 1956 г.
6. техн. количество информации, которое может быть записано на какой-либо носитель (например, на дискету, жёсткий диск)
Делаем Карту слов лучше вместе
Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова сплачиваться (глагол), сплачиваются:
Источник статьи: http://kartaslov.ru/%D0%B7%D0%BD%D0%B0%D1%87%D0%B5%D0%BD%D0%B8%D0%B5-%D1%81%D0%BB%D0%BE%D0%B2%D0%B0/%D1%91%D0%BC%D0%BA%D0%BE%D1%81%D1%82%D1%8C
Электроемкость и конденсаторы
Напряжение, которое возникает между двумя по-разному заряженными телами, зависит от многих параметров – в первую очередь, от геометрических размеров тел, их электрических свойств, а также от свойств окружающей среды. Однако, пропорциональность этого напряжения заряду всегда сохраняется. Данное обстоятельство позволяет ввести специальную величину, характеризующую способность тел накапливать заряды – электроемкость (обозначается латинской буквой $C$).
Рис. 2. Электроемкость.
Как правило, в реальных электрических схемах для создания электроемкости в качестве заряженных тел используются проводящие пластины, а чтобы создаваемые на них заряды не смешивались и не компенсировали друг друга, пространство между пластинами заполняется диэлектриком (например, воздухом).
Рис. 3. Переменный конденсатор с воздушным диэлектриком.
Конденсаторам, обладающим большой емкостью, легко передавать заряды, для этого требуется совершить мало работы. Конденсаторам с малой емкостью, наоборот, заряды передавать трудно, работы для этого требуется больше. Поскольку работа, совершаемая при переносе заряда, характеризуется потенциалом, то емкость конденсатора будет равна отношению переданного заряда к разности потенциалов (напряжению) между обкладками:
$$С ={q \over U}$$
Из данной формулы можно вывести единицу электроемкости – Фарад. Фарад – это емкость конденсатора, у которого при передаче ему заряда в 1 Кулон на обкладках возникнет напряжение 1 Вольт:
$$1Ф ={1 Кл \over 1В}$$
1 Фарад – это очень большая емкость. Конденсаторы, использующиеся в силовой электротехнике, имеют емкость, порядка десятков и сотен микрофарад. Конденсаторы, использующиеся в высокочастотной радиотехнике (например, изображенный выше), имеют емкости порядка десятков и даже единиц пикофарад ($1пФ = 10^{-12}Ф$).
Что мы узнали?
Электроемкость – это способность тел накапливать электрические заряды. Единицей электроемкости является Фарад. В реальных схемах для создания электроемкости используются конденсаторы, состоящие из проводящих пластин, разделенных диэлектриком.
Тест по теме
-
Вопрос 1 из 5
При электризации тел…
- повышается температура тел
- телам сообщается некоторый электрический заряд
- изменяется форма тел
- телам придается некоторое ускорение
Начать тест(новая вкладка)
Принцип работы конденсаторов
При подсоединении цепи к источнику электрического тока через конденсатор начинает течь электрический ток. В начале прохождения тока через конденсатор его сила имеет максимальное значение, а напряжение – минимальное. По мере накопления устройством заряда сила тока падает до полного исчезновения, а напряжение увеличивается.
В процессе накопления заряда электроны скапливаются на одной пластинке, а положительные ионы – на другой. Между пластинами заряд не перетекает из-за присутствия диэлектрика. Так устройство накапливает заряд. Это явление называется накоплением электрических зарядов, а конденсатор –накопителем электрического поля.
Единица измерения емкости
В Международной системе СИ за единицу измерения ёмкости конденсатора принимают фарад:
= Ф, где С – обозначение ёмкости устройства.
Международное обозначение – F. Названа в честь английского физика М.Фарадея и используется в Международной системе СИ с 1960г.
Формула для расчёта электроёмкости записывается следующим образом:
С = Dq / U (1), где:
- Dq – заряд (измеряется в кулонах, или Кл),
- U – разность потенциалов между обкладками (измеряется в вольтах или В).
Следовательно, 1Ф = 1Кл / 1В.
То есть конденсатор ёмкостью в 1 фарад накапливает на обкладках заряд, равный 1 кулон, создавая напряжение между ними, равное 1 вольт.
В фарадах измеряются электроёмкости проводников и конденсаторов.
Согласно правилам написания, принятых в СИ, если название происходит от фамилии учёного, то полное её название «фарад» пишется с маленькой (строчной) буквы, а её сокращённое название «Ф» – с прописной.
Единица измерения электроёмкости в других системах
Помимо СИ, есть ещё устаревшая система СГС, которой пользовались ранее. Первые три символа в названии обозначают:
- С – сантиметр,
- Г – грамм,
- С – секунда.
- 1см » 1,1126 · 10-12Ф,
- 1Ф » 8,99 · 1011 статФ.
Сантиметр по-другому может называться статфарад, или статФ.
В системе СГСМ единицей измерения является абфарад, или абФ. Абфарад связан с фарадом следующим образом:
1абф = 1·109 Ф = 1ГФ.
Для перевода из СГСЭ и СГСМ в СИ в сети Интернет имеются специальные сервисы, которые позволяют автоматизировать эти действия.
Онлайн переводчик из СГС в СИ
Единица и формулы расчёта
Ёмкость в виде электрического свойства, способного хранить заряды, измеряется в фарадах (Ф) и обозначается С. Величина названа в честь английского физика Майкла Фарадея. Конденсатор ёмкостью 1 фарад способен хранить заряд в 1 кулон на пластинах с напряжением 1 вольт. Значение С всегда положительно.
Математическое выражение фарада
Ёмкость конденсатора — постоянная величина, означающая потенциальную способность хранить энергию. Количество заряда, хранимое в отдельно взятый момент, определяется уравнением Q=CV, где V — приложенное напряжение. Таким образом, регулируя напряжение на пластинах, можно увеличивать или уменьшать заряд. Эта формула ёмкости в виде C=Q/V в единичных значениях определяет, в чём измеряется ёмкость конденсатора в СИ, и является математическим выражением фарада.
Специалисты по электронике единицу в один фарад считают не совсем практичной, поскольку она представляет собой огромное значение. Даже 1/1000 F — это очень большая ёмкость. Как правило, для реальных электрических компонентов применяют следующие величины:
- пикофарад — 10—12 Ф;
- нанофарад — 10—9 Ф;
- микрофарад — 10—6 Ф.
Вам это будет интересно Защита электросети с помощью автоматического выключателя
Диэлектрическая проницаемость
Фактор, благодаря которому изолятор определяет ёмкость конденсатора, называется диэлектрической проницаемостью. Обобщённая формула расчёта ёмкости конденсатора с параллельными пластинами представлена выражением C= ε (A / d), где:
- А — площадь меньшей пластины;
- d — расстояние между ними;
- ε — абсолютная проницаемость используемого диэлектрического материала.
Диэлектрическая проницаемость вакуума ε0 является константой и имеет значение 8,84х10—12 фарад на метр. Как правило, проводящие пластины разделены слоем изоляционного материала, а не вакуума. Чтобы найти ёмкость конденсатора, пластины которого находятся в воздухе, можно воспользоваться значением ε0. Разницей диэлектрической проницаемости атмосферы и вакуума можно пренебречь, поскольку их значения очень близки.
На практике в формулах нахождения ёмкости конденсатора используется относительная диэлектрическая проницаемость в качестве коэффициента, означающая, насколько электрическое поле между зарядами уменьшается в диэлектрике по сравнению с вакуумом. Некоторые значения этой величины для различных материалов:
- 1,0006 — воздух;
- 2,5—3,5 — бумага;
- 3—10 — стекло;
- 5—7 — слюда.
Что такое электроемкость проводников
Если у нас есть два проводника, изолированных друг от друга, которым мы сообщаем некоторые заряды (обозначим их соответственно q1 и q2), то между ними возникнет определенная разность потенциалов. Ее величина будет зависеть от формы проводников, а также от исходных величин зарядов. Обозначим такую разность Δφ. Если мы говорим о разности, возникающей в электрическом поле между двумя точками, то ее обычно обозначают U.
В рамках темы данной статьи нам больше всего интересна такая разность потенциалов между проводниками, когда их заряды противоположны по знаку, но равны друг другу по модулю. В таком случае мы можем ввести новое понятие – электрическая емкость (электроемкость).
Определение 1
Электрической емкостью системы, состоящей из двух проводников, называется отношение заряда одного проводника (q) к разности потенциалов между этими двумя проводниками.
В виде формулы это записывается так: C=q∆φ=qU.
Для измерения электрической емкости применяется единица, называемая фарад. Она обозначается буквой Ф.
1Φ=1 Кл1 В.
Конфигурации и размеры проводников, а также свойства диэлектрика определяют величину электроемкости заданной системы. Наибольший интерес для нас представляют проводники особой формы, называемые конденсаторами.
Определение 2
Конденсатор – это проводник, конфигурация которого позволяет локализовать (сосредотачивать) электрическое поле в одной выделенной части пространства. Проводники, составляющие конденсатор, называются обкладками.
Определение 3
Если мы возьмем две плоские пластины из проводящего материала, расположим их на небольшом расстоянии друг от друга и проложим между ними слой диэлектрика, то мы получим простейший конденсатор, называемый плоским. При его работе электрическое поле будет располагаться преимущественно в промежутке между пластинами, но небольшая часть этого поля будет рассеиваться вокруг них.
Определение 4
Часть электрического поля вблизи конденсатора называется полем рассеяния.
Иногда в задачах мы можем не учитывать его и работать только с той частью электрического поля, которое расположено между обкладками. Однако пренебрегать полем рассеяния допустимо далеко не всегда, поскольку это может привести к ошибочным расчетам из-за нарушения потенциального характера электрического поля.
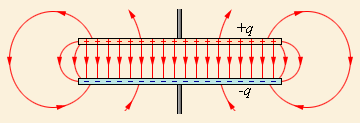
Рисунок 1.6.1. Электрическое поле в плоском конденсаторе.
Рисунок 1.6.2. Электрическое поле конденсатора без учета поля рассеяния, не обладающее потенциальностью.
Модуль напряженности электрического поля, которое создает каждая обкладка в плоском конденсаторе, выражается соотношением следующего вида:
E1=σ2ε.
Исходя из принципа суперпозиции, можно утверждать, что напряженность E→ поля, которое создают обе пластины конденсатора, будет равна сумме напряженностей E+→ и E-→ полей каждой пластины, то есть E→=E+→+E-→.
Векторы напряженностей обеих пластин во внутренней части конденсатора будут параллельны друг другу. Значит, мы можем выразить модуль напряженности их суммарного поля в виде формулы E=2E1=σε.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Расчёт ёмкости плоских конденсаторов
Конденсатор — для чего нужен, устройство и принцип работы
В идеальных условиях для определения емкости конденсатора (C) можно применить формулу:
С0 = q/ U.
Диэлектрические свойства промежуточного слоя учитывают дополнением C = C0 * e.
Базовая единица (фарад или сокращенно Ф) слишком велика для типовых электротехнических схем. Поэтому применяют кратные уменьшительные приставки:
- миллифарад (мФ) – 10-3 Ф;
- микрофарад (мкФ) – 10-6 Ф;
- нанофарад (нФ) – 10-9 Ф;
- пикофарад (пФ) – 10-12 Ф.
Емкость один фарад соответствует накопленному единичному заряду (1 Кл), который создает разницу потенциалов на пластинах 1 В. По формуле емкости шара можно вычислить потенциал Земли –700 микрофарад.
Практические измерения
Значение ёмкости конденсатора обозначается на корпусе в дробных фарадах или с помощью цветового кода. Но со временем компоненты способны потерять свои качества, поэтому для некоторых критических случаев последствия могут быть неприемлемыми. Существуют и другие обстоятельства, требующие измерений. Например, необходимость знать общую ёмкость цепи или части электрооборудования. Приборов, осуществляющих непосредственное считывание ёмкости, не существует, но значение может быть вычислено вручную или интегрированными в измерительные устройства процессорами.
Для обнаружения фактической ёмкости нередко используют осциллограф как средство измерения постоянной времени (т). Эта величина обозначает время в секундах, за которое конденсатор заряжается на 63%, и равна произведению сопротивления цепи в омах на ёмкость цепи в фарадах: т=RC. Осциллограф позволяет легко определить постоянную времени и даёт возможность с помощью расчётов найти искомую ёмкость.
Существует также немало моделей любительского и профессионального электронного измерительного оборудования, оснащённого функциями для тестирования конденсаторов. Многие цифровые мультиметры обладают возможностью определять ёмкость. Эти устройства способны контролируемо заряжать и разряжать конденсатор известным током и, анализируя нарастание результирующего напряжения, выдавать довольно точный результат. Единственный недостаток большинства таких приборов — сравнительно узкий диапазон измеряемых величин.
Вам это будет интересно Выбор и особенности подключения счётчика энергомера
https://youtube.com/watch?v=8TpQzXyb9u4
Конденсатор постоянной емкости
Конденсаторы, емкость которых изменять нельзя, называются конденсаторами постоянной емкости.
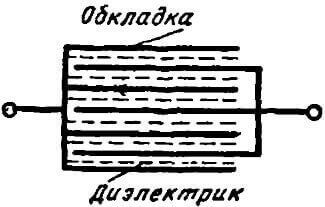
Рисунок 2. Схема устройства конденсаторапостоянной емкости
Наиболее распространенные в настоящее время конденсаторы постоянной емкости состоят из очень тонких металлических (станиолевых) листов с парафинированной бумажной или слюдяной прослойкой между ними.
Для увеличения емкости (увеличения площади пластин конденсатора) чаще всего берут по нескольку станиолевых листов и соединяют их в две группы, входящие одна в другую и разделенные диэлектриком, как схематически показано на рисунке 2. Иногда также берут две длинные станиолевые пластины, прокладывают между ними и снаружи парафинированную бумагу и затем свертывают все в компактный пакет или трубку. Конденсаторы большой емкости во многих случаях помещают в металлическую коробку и заливают парафином.

Рисунок 3. Внешний вид современных конденсаторов постоянной емкости
Определим емкость плоского конденсатора. Возьмем произвольную замкнутую поверхность вокруг одной из пластин конденсатора. Тогда по теореме Гаусса поток вектора напряженности, проходящий через любую замкнутую поверхность, внутри которой находится электрический заряд, равен:
| (1) |
Предполагая, что поле конденсатора однородно (пренебрегая искажением поля у краев пластин), получаем напряженность электрического поля в конденсаторе:
| (2) |
где d – расстояние между пластинами или толщина диэлектрика. Подставив значение E из формулы (2) в формулу (1), получим:
откуда
Так как
то выражение емкости плоского конденсатора примет вид:
где S – площадь пластин в м²; d – толщина диэлектрика в м; ε – относительная электрическая проницаемость диэлектрика (диэлектрическая проницаемость).
Таким образом, для увеличения емкости плоского конденсатора нужно увеличить площадь его пластин (обкладок) S, уменьшить расстояние между ними d и в качестве диэлектрика поставить материал с большой относительной электрической проницаемостью (ε).
Видео об устройстве конденсатора постоянной емкости:
https://youtube.com/watch?v=2FrHllRJ654
Соединение конденсаторов
Во многих случаях, чтобы создать нужную электроемкость, конденсаторы соединяют в группу, которая называется батареей.
Последовательным называют такое соединение конденсаторов, при котором отрицательно заряженная обкладка предварительного конденсатора соединена с положительно заряженной обкладкой следующего. В случае последовательного соединения на всех обкладках конденсаторов будут одинаковые по модулю заряды, соответственно одинаковыми будут и потенциалы обкладок, соединенных между собой проводниками.
Учтя это, выведем формулу для вычисления электроемкости батареи последовательно соединенных конденсаторов. Напряжение на батарее U бы равна сумме напряжений на последовательно соединенных конденсаторах, действительно (φ 1 — φ 2 ) + (φ 2 — φ 3 ) + … + (φ n -1 — φ n ) = φ 1 — φ n или U 1 + U 2 + … + U n = U бы . Использовав соотношение q = CU, получим
Сократив на q, получим
Следовательно, для последовательного соединение электроемкость батареи меньше наименьшей из электроемкости отдельных конденсаторов.
Параллельным называется соединение конденсаторов, при котором все положительно заряженные обкладки присоединены к одному проводнику, а отрицательно заряженные — к другому. В этом случае напряжения на всех конденсаторах одинаковы и равны U, а заряд на батареи равна сумме зарядов на отдельных конденсаторах, q б = q 1 + q 2 + … + q n , откуда C бы U = C 1 U + C 2 U + … + C n U. После сокращения получаем формулу для вычисления электроемкости батареи параллельно соединенных конденсаторов, С б = C 1 + C 2 + … + C n. Для параллельного соединения электроемкость батареи больше, чем самая большая из электроемкости отдельных конденсаторов (равна сумме емкостей всех конденсаторов).
Энергия заряженного конденсатора. Как и любая система заряженных тел, конденсатор обладает энергией. Для того чтобы зарядить конденсатор, нужно выполнить работу, затрачиваемое на разделение положительных и отрицательных зарядов. Согласно закону сохранения энергии, эта работа равна энергии конденсатора A = W эл .
Как известно, работа сил электрического поля по перемещению заряда на определенное расстояние равно A = qU, если напряжение постоянное (U = const). В случае подзарядки конденсатора напряжение на его обкладках растет от нуля до U, и, вычисляя работу поля, в этом случае нужно использовать ее среднее значение
соответственно энергия заряженного конденсатора
Поскольку q = CU, то получим еще две формулы для вычисления энергии конденсатора:
Конденсаторы
Для практического использования электрической энергии необходимо уметь ее накапливать. Для этого используют специальные устройства — конденсаторы.
Конденсаторы — это устройства, которые состоят из двух или более проводников, разделенных тонким слоем диэлектрика.
Проводники, из которых состоит конденсатор, называются обкладками
Как правило, при зарядке конденсатора заряды его обкладок равны по величине и противоположны по знаку. Под зарядом конденсатора
понимают значение заряда положительно заряженной обкладки.
Термин «конденсатор » от латинского слова condensare — сгущать ввел А.Вольта (итальянский физик) в 1782 г. Первые электрические конденсаторы были изготовлены Э.Клейстом и П. Ван Мушенбреком в 1745 г. По имени города Лейдена, где работал Мушенбрек, французкий физик Жан Нолле назвал их лейденскими банками.
При небольших размерах конденсатор отличается значительной емкостью, не зависящей от наличия вблизи него других зарядов или проводников.
Электроемкостью конденсатора называют физическую величину, численно равную отношению заряда конденсатора к разности потенциалов между его обкладками:
\(~C = \dfrac{q}{\varphi_1 — \varphi_2}\) или \(~C = \dfrac qU .\)
Из этой формулы видно, что чем больше напряжение между обкладками конденсатора, тем больше на них заряд. Но для каждого конденсатора существует предельное (максимальное)напряжение , выше которого диэлектрик начнет разрушаться. При этом заряды обкладок конденсатора мгновенно нейтрализуются, происходитпробой , т.е. конденсатор выходит из строя.
Виды конденсаторов
Конденсаторы можно классифицировать по следующим признакам и свойствам:
- по форме обкладок различают конденсаторы плоские, сферические, цилиндрические и др.;
- по типу диэлектрика (рис. 1) —бумажные (а), воздушные (б), слюдяные, керамические, электролитические (в) и т.д.;
- по рабочему напряжению — низковольтные (напряжение пробоя до 100 В) и высоковольтные (выше 100 В);
- по возможности изменения своей емкости — постоянной емкости (см. рис. 1, а, в), переменной емкости (см. рис. 1, б), подстроечные (рис. 2).
- а
- б
- в
Рис. 1
- Рис. 2
- Рис. 3
Другие виды конденсаторов показаны на рисунке 3.
См. так же Wikipedia Классификация конденсаторов
Электроемкость плоского конденсатора C
зависит от площади обкладокS , расстояния между нимиd и диэлектрической проницаемости диэлектрика ε, заполняющего пространство между обкладками конденсатора, но не зависит от материала, из которого эти пластины изготовлены \(~C = \dfrac{\varepsilon_0 \cdot \varepsilon \cdot S}{d},\) где ε0 — электрическая постоянная.
*Вывод формулы
Поле плоского конденсатора можно рассматривать как совокупность полей двух бесконечных разноименно заряженных плоскостей (рис. 2, а и б). Напряженность поля (рис. 2, в) можно найти по принципу суперпозиции:
\(\vec{E}=\vec{E}_{1} +\vec{E}_{2},\)
где \( E_{1} = E_{2} =\dfrac{\sigma }{2\varepsilon _{0} \cdot \varepsilon } =\dfrac{q}{2\varepsilon _{0} \cdot \varepsilon \cdot S}\) — напряженности электрических полей каждой из обкладок конденсатора, σ
— поверхностная плотность заряда на обкладках конденсатора. Тогда в проекциях на ось 0Х:
справа и слева от пластин — \(E_х = 0\);
между пластин — \(E=2E_{1} =\dfrac{q}{\varepsilon _{0} \cdot \varepsilon \cdot S}.\)
- а
- б
- в
Рис. 4 Электроемкость плоского конденсатора \(~C = \dfrac qU\), где \(U = E \cdot d,\) d
— расстояние между пластин. Следовательно, \(C =\dfrac{q}{E\cdot d} = \dfrac{q}{d} \cdot \dfrac{1}{E} = \dfrac{q}{d} \cdot \dfrac{\varepsilon _{0} \cdot \varepsilon \cdot S}{q} = \dfrac{\varepsilon _{0} \cdot \varepsilon \cdot S}{d}.\).
- При быстром разряде конденсатора можно получить импульс большой мощности, например, в фотовспышках, электромагнитных ускорителях, импульсных лазерах и т. п.
- Так как конденсатор способен длительное время сохранять заряд, то его можно использовать в качестве элемента памяти или устройства хранения электрической энергии.
- Емкость конденсатора заметно изменяется при малейших изменениях параметра конденсатора. Так малое изменение расстояния между обкладками учитывается в измерителях малых перемещений, изменение состава диэлектрика при изменении влажности фиксируется в измерителях влажности, учет изменения высоты диэлектрика между обкладками конденсатора позволяет измерять уровень жидкости и т.п.
- Конденсаторы (совместно с катушками индуктивности и/или резисторами) используются для построения различных цепей с частотно-зависимыми свойствами, в частности, фильтров, цепей обратной связи, колебательных контуров и т. п.





