Содержание
1.2 Двоичная
В предыдущем примере мы перевели все десятичные числа в другие системы счислений, одна из которых двоичная. Теперь переведем каждое число с двоичной формы.
1.2.1 Двоичная → Десятичная
Для перевода чисел с двоичной формы в десятичную нужно знать два нюанса. Первый – у каждого нолика и единички есть множитель 2 в n-й степени, при котором n увеличивается справа налево ровно на единичку. Второй – после перемножения все числа нужно сложить и мы получим число в десятичной форме. В итого у нас будет формула такого вида:
Где,D – это число в десятичной форме, которое мы ищем;n – количество символов в двоичном числе;a – число в двоичной форме на n-й позиции (т.е. первый символ, второй, и т.п.);p – коэффициент, равный 2,8 или 16 в степени n (в зависимости от системы счисления)
К примеру возьмем число 110102. Смотрим на формулу и записываем:
- Число состоит из 5 символов (n=5)
-
a5 = 1, a4 = 1, a3 = 0, a2 = 1, a1 = 0
- p = 2 (так как переводим из двоичной в десятичную)
В итоге имеем:
Кто привык записывать справа на лево, форму будет выглядеть так:
Но, как мы знаем, от перестановки слагаемых сумма не меняется. Давайте теперь переведем наши числа в десятичную форму.
Рисунок 1.5 – Перевод чисел из двоичной в десятичную систему
1.2.2 Двоичная → Восьмеричная
При переводе нам нужно двоичное число разбить на группы по три символа справа налево. Если последняя группа не состоит из трех символов, то мы просто возмещаем недостающие биты ноликами. К примеру:
10101001 = 10 101 001
1011100 = 001 011 100
Каждая группа битов – это одно из восьмеричных чисел. Чтобы узнать какое, нужно использовать написанную выше формулу 1.2.1 для каждой группы битов. В результате мы получим.
Рисунок 1.6 – Перевод чисел из двоичной в восьмеричную систему
1.2.3 Двоичная → Шестнадцатеричная
Здесь нам нужно двоичное число разбивать на группы по четыре символа справа налево с последующим дополнением недостающих битов группы ноликами, как писалось выше. Если последняя группа состоит из ноликов, то их нужно игнорировать.
110101011 = 0001 1010 1011
1011100 = 101 1100
001010000 = 000101 0000 = 0101 0000
Каждая группа битов – это одно из шестнадцатеричных чисел. Используем формулу 1.2.1 для каждой группы битов.
Рисунок 1.7 – Перевод чисел из двоичной в шестнадцатеричную систему
Знаковое представление величины
Это представление также называется представлением «знак-величина» или «знак и величина». В этом подходе знак числа представлен битом знака : установка этого бита (часто самого старшего бита ) на 0 для положительного числа или положительного нуля и установка на 1 для отрицательного числа или отрицательного нуля. Остальные биты числа указывают величину (или абсолютное значение ). Например, в восьмибитном байте только семь битов представляют величину, которая может находиться в диапазоне от 0000000 (0) до 1111111 (127). Таким образом, числа в диапазоне от -127 10 до +127 10 могут быть представлены после добавления знакового бита (восьмого бита). Например, -43 10, закодированный в восьмибитном байте, составляет 1 0101011, а 43 10 — 0101011. Использование представления величины со знаком имеет несколько последствий, что делает их более сложными для реализации:
- Есть два способа представить ноль: 00000000 (0) и 10000000 ( -0 ).
- Сложение и вычитание требуют разного поведения в зависимости от знакового бита, тогда как одно дополнение может игнорировать знаковый бит и просто выполнять сквозной перенос, а два дополнения могут игнорировать знаковый бит и зависеть от поведения переполнения.
- Сравнение также требует проверки знакового бита, тогда как в дополнении до двух можно просто вычесть два числа и проверить, является ли результат положительным или отрицательным.
- Минимальное отрицательное число -127 вместо -128 в случае дополнения до двух.
Этот подход напрямую сопоставим с обычным способом показа знака (размещение «+» или «-» рядом с величиной числа). Некоторые ранние бинарные компьютеры (например, IBM 7090 ) использовали это представление, возможно, из-за его естественного отношения к обычному использованию. Величина со знаком — это наиболее распространенный способ представления мантиссы в значениях с плавающей запятой .
Ссылки [ править ]
- ^ Choo, Hunsoo; Мухаммад, К .; Рой, К. (февраль 2003 г.). «Множитель совместного использования вычислений с дополнением до двух и его приложения к высокопроизводительному DFE» . Транзакции IEEE по обработке сигналов . 51 (2): 458–469. DOI : 10.1109 / TSP.2002.806984 .
- ^ Справочное руководство по программированию GE-625/635 . General Electric . Январь 1966 . Проверено 15 августа 2013 года .
- ^ Руководство разработчика программного обеспечения для архитектур Intel 64 и IA-32 . Intel . Раздел 4.2.1 . Проверено 6 августа 2013 года .
- ^ Power ISA версии 2.07 . Power.org . Раздел 1.4 . Проверено 6 августа 2013 года .,
- ^ Бэкон, Джейсон В. (2010–2011). «Информатика 315 Конспект лекций» . Проверено 21 февраля 2020 года .
- ^ US 4484301 , «Array мультипликатор работает в одном формате дополнения», выпущенный 1981-03-10
- ^ США 6760440 , «поразрядное дополнение криптографической объединитель», выданная 1999-12-11
- ^ Шедлецкий, Джон Дж. (1977). «Комментарий к последовательному и неопределенному поведению сумматора с непрерывным переносом» . Транзакции IEEE на компьютерах . 26 (3): 271–272. DOI10.1109 / TC.1977.1674817 .
- ^ Дональд Кнут: Искусство компьютерного программирования , том 2: получисловые алгоритмы, глава 4.1
- ↑ Томас Финли (апрель 2000 г.). «Два дополнения» . Корнельский университет . Проверено 15 сентября 2015 года .
- ^ Буферы протокола: целые числа со знаком
- Иван Флорес, Логика компьютерной арифметики , Прентис-Холл (1963)
- Исраэль Корен, Компьютерные арифметические алгоритмы , AK Peters (2002), ISBN 1-56881-160-8
База -2 [ править ]
В обычных двоичных системах счисления основание или основание системы счисления равно 2; таким образом, крайний правый бит представляет 2 , следующий бит представляет 2 1 , следующий бит 2 2 и так далее. Однако возможна и двоичная система счисления с основанием −2. Самый правый бит представляет (-2) = +1 , следующий бит представляет (-2) 1 = -2 , следующий бит (-2) 2 = +4 и так далее, с переменным знаком. Числа, которые могут быть представлены четырьмя битами, показаны в сравнительной таблице ниже.
Диапазон чисел, которые могут быть представлены, асимметричен. Если слово имеет четное число битов, величина наибольшего отрицательного числа, которое может быть представлено, вдвое больше, чем наибольшее положительное число, которое может быть представлено, и наоборот, если слово имеет нечетное число битов.
История [ править ]
Первые дни цифровых вычислений были отмечены множеством конкурирующих идей как в отношении аппаратных технологий, так и математических технологий (систем счисления). Одним из самых больших споров был формат отрицательных чисел, некоторые из ведущих экспертов эпохи имели очень сильные и разные мнения. [ необходима цитата ] Один лагерь поддерживал два дополнения , систему, которая сегодня доминирует. Другой лагерь поддерживал дополнение, где любое положительное значение превращается в его отрицательный эквивалент путем инвертирования всех битов в слове. Третья группа поддерживает «знак и величину» (знак-величина), где значение изменяется с положительного на отрицательное просто путем переключения бита знака (старшего разряда) слова.
Были аргументы за и против каждой из систем. Знак и величина позволили упростить отслеживание дампов памяти (распространенный процесс в 1960-х годах), поскольку для небольших числовых значений используется меньше 1 бит. Внутри этих систем выполнялась математика с дополнением единиц, поэтому числа должны были быть преобразованы в значения дополнения единиц, когда они были переданы из регистра в математический блок, а затем преобразованы обратно в знаковую величину, когда результат был передан обратно в регистр. Электронике требовалось больше вентилей, чем другим системам, что было ключевой проблемой, когда стоимость и упаковка дискретных транзисторов были критическими. IBM была одним из первых сторонников знаковой величины, и их компьютеры серий , и 709x были, пожалуй, самыми известными системами, в которых она использовалась.
Их дополнение позволило несколько упростить конструкцию оборудования, поскольку не было необходимости преобразовывать значения при передаче в математический блок и из него. Но у него также есть нежелательная характеристика со знаком-величиной — способность представлять отрицательный ноль (-0). Отрицательный ноль ведет себя точно так же, как положительный ноль; при использовании в качестве операнда в любом вычислении результат будет одинаковым независимо от того, является ли операнд положительным или отрицательным нулем. Однако недостатком является то, что наличие двух форм одного и того же значения требует двух, а не одного сравнения при проверке равенства нулю. Вычитание дополнительных элементов также может привести к заимствованию на конец периода.(описано ниже). Можно утверждать, что это усложняет логику сложения / вычитания или упрощает ее, поскольку вычитание требует простого инвертирования битов второго операнда при его передаче в сумматор. PDP-1 , CDC 160 серии , CDC 3000 серии, CDC серии 6000 , UNIVAC 1100 серии, а также ЛИНК дополнение представление компьютера использовать поразрядное.
Дополнение до двух проще всего реализовать на оборудовании, что может быть основной причиной его широкой популярности. Процессоры на ранних мэйнфреймах часто состояли из тысяч транзисторов — устранение значительного количества транзисторов было значительной экономией. Мэйнфреймы , такие как IBM System / 360 , в серии GE-600 , и PDP-6 и PDP-10 использовать два с дополнением, как и миникомпьютеры , такие , как PDP-5 и PDP-8 и PDP-11 и VAX . Архитекторы первых процессоров на базе интегральных схем ( Intel 8080и т. д.) решили использовать математику с дополнением до двух. По мере развития технологии ИС практически все использовали технологию дополнения до двух. Процессоры x86 , m68k , Power ISA , MIPS , SPARC , ARM , Itanium , PA-RISC и DEC Alpha дополняют друг друга.
Сравнительная таблица
В следующей таблице показаны положительные и отрицательные целые числа, которые можно представить с помощью четырех битов.
| Десятичный | Неподписанный | Знак и величина | Дополнение | Два дополнения | Превышение-8 (необъективно) | База −2 |
|---|---|---|---|---|---|---|
| +16 | Нет данных | Нет данных | Нет данных | Нет данных | Нет данных | Нет данных |
| +15 | 1111 | Нет данных | Нет данных | Нет данных | Нет данных | Нет данных |
| +14 | 1110 | Нет данных | Нет данных | Нет данных | Нет данных | Нет данных |
| +13 | 1101 | Нет данных | Нет данных | Нет данных | Нет данных | Нет данных |
| +12 | 1100 | Нет данных | Нет данных | Нет данных | Нет данных | Нет данных |
| +11 | 1011 | Нет данных | Нет данных | Нет данных | Нет данных | Нет данных |
| +10 | 1010 | Нет данных | Нет данных | Нет данных | Нет данных | Нет данных |
| +9 | 1001 | Нет данных | Нет данных | Нет данных | Нет данных | Нет данных |
| +8 | 1000 | Нет данных | Нет данных | Нет данных | Нет данных | Нет данных |
| +7 | 0111 | 0111 | 0111 | 0111 | 1111 | Нет данных |
| +6 | 0110 | 0110 | 0110 | 0110 | 1110 | Нет данных |
| +5 | 0101 | 0101 | 0101 | 0101 | 1101 | 0101 |
| +4 | 0100 | 0100 | 0100 | 0100 | 1100 | 0100 |
| +3 | 0011 | 0011 | 0011 | 0011 | 1011 | 0111 |
| +2 | 0010 | 0010 | 0010 | 0010 | 1010 | 0110 |
| +1 | 0001 | 0001 | 0001 | 0001 | 1001 | 0001 |
| +0 | 0000 | 0000 | 0000 | 0000 | 1000 | 0000 |
| −0 | 1000 | 1111 | ||||
| −1 | Нет данных | 1001 | 1110 | 1111 | 0111 | 0011 |
| −2 | Нет данных | 1010 | 1101 | 1110 | 0110 | 0010 |
| −3 | Нет данных | 1011 | 1100 | 1101 | 0101 | 1101 |
| −4 | Нет данных | 1100 | 1011 | 1100 | 0100 | 1100 |
| −5 | Нет данных | 1101 | 1010 | 1011 | 0011 | 1111 |
| −6 | Нет данных | 1110 | 1001 | 1010 | 0010 | 1110 |
| −7 | Нет данных | 1111 | 1000 | 1001 | 0001 | 1001 |
| −8 | Нет данных | Нет данных | Нет данных | 1000 | 0000 | 1000 |
| −9 | Нет данных | Нет данных | Нет данных | Нет данных | Нет данных | 1011 |
| −10 | Нет данных | Нет данных | Нет данных | Нет данных | Нет данных | 1010 |
| −11 | Нет данных | Нет данных | Нет данных | Нет данных | Нет данных | Нет данных |
Та же таблица, если смотреть со стороны «учитывая эти двоичные биты, какое число интерпретируется системой представления»:
| Двоичный | Неподписанный | Знак и величина | Дополнение | Два дополнения | Превышение-8 | База −2 |
|---|---|---|---|---|---|---|
| 0000 | −8 | |||||
| 0001 | 1 | 1 | 1 | 1 | −7 | 1 |
| 0010 | 2 | 2 | 2 | 2 | −6 | −2 |
| 0011 | 3 | 3 | 3 | 3 | −5 | −1 |
| 0100 | 4 | 4 | 4 | 4 | −4 | 4 |
| 0101 | 5 | 5 | 5 | 5 | −3 | 5 |
| 0110 | 6 | 6 | 6 | 6 | −2 | 2 |
| 0111 | 7 | 7 | 7 | 7 | −1 | 3 |
| 1000 | 8 | −0 | −7 | −8 | −8 | |
| 1001 | 9 | −1 | −6 | −7 | 1 | −7 |
| 1010 | 10 | −2 | −5 | −6 | 2 | −10 |
| 1011 | 11 | −3 | −4 | −5 | 3 | −9 |
| 1100 | 12 | −4 | −3 | −4 | 4 | −4 |
| 1101 | 13 | −5 | −2 | −3 | 5 | −3 |
| 1110 | 14 | −6 | −1 | −2 | 6 | −6 |
| 1111 | 15 | −7 | −0 | −1 | 7 | −5 |
Нормализованная запись числа.
Нормализованная запись отличного от нуля действительного числа – это запись вида a= m*P q , где q – целое число (положительное, отрицательное или ноль), а m – правильная P-ичная дробь, у которой первая цифра после запятой не равна нулю, то есть . При этом m называется мантиссой числа, q – порядком числа.
Примеры:
- 3,1415926 = 0, 31415926 * 10 1 ;
- 1000=0,1 * 10 4 ;
- 0,123456789 = 0,123456789 * 10 0 ;
- 0,00001078 = 0,1078 * 8 -4 ; (порядок записан в 10-й системе)
- 1000,00012 = 0, 100000012 * 2 4 .
Так как число ноль не может быть записано в нормализованной форме в том виде, в каком она была определена, то считаем, что нормализованная запись нуля в 10-й системе будет такой: 0 = 0,0 * 10 0 .
Нормализованная экспоненциальная запись числа – это запись вида a= m*P q , где q – целое число (положительное, отрицательное или ноль), а m – P-ичная дробь, у которой целая часть состоит из одной цифры. При этом (m-целая часть) называется мантиссой числа, q – порядком числа.
Кодирование вещественных чисел
Несколько иной способ применяется для представления в памяти
персонального компьютера действительных чисел. Рассмотрим представление
величин с плавающей точкой.
Любое действительное число можно записать в стандартном виде M × 10p,
где 1 £ M p целое. Например, 120100000 = 1,201 × 108. Поскольку
каждая позиция десятичного числа отличается от соседней на степень числа
10, умножение на 10 эквивалентно сдвигу десятичной запятой на одну позицию
вправо. Аналогично деление на 10 сдвигает десятичную запятую на позицию
влево. Поэтому приведенный выше пример можно продолжить: 120100000 = 1,201 × 108 = 0,1201 × 109 = 12,01 × 107. Десятичная запятая «плавает» в числе
и больше не помечает абсолютное место между целой и дробной частями.
В приведенной выше записи M называют мантиссой числа, а p его
порядком. Для того чтобы сохранить максимальную точность, вычислительные
машины почти всегда хранят мантиссу в нормализованном виде, что означает,
что мантисса в данном случае есть число, лежащее между 1(10) и 2(10) (1 £ M
Современный персональный компьютер
позволяет работать со следующими действительными типами (диапазон значений
указан по абсолютной величине; в некоторых случаях перечень типов данных может быть расширен):
| Тип | Диапазон | Мантисса | Байты |
|---|---|---|---|
| Real | 2,9×10-39..1,7×1038 | 11-12 | 6 |
| Single | 1,5×10-45..3,4×1038 | 7-8 | 4 |
| Double | 5,0×10-324..1,7×10308 | 15-16 | 8 |
| Extended | 3,4×10-4932..1,1×104932 | 19-20 | 10 |
Покажем преобразование действительного числа для представления его в
памяти ЭВМ на примере величины типа Double.
Как видно из таблицы, величина это типа занимает в памяти 8 байт. На
рисунке ниже показано, как здесь представлены поля мантиссы и порядка (нумерация битов осуществляется справа налево):
| S | Смещенный порядок | Мантисса |
| 63 | 62..52 | 51..0 |
Можно заметить, что старший бит, отведенный под мантиссу, имеет номер
51, т.е. мантисса занимает младшие 52 бита. Черта указывает здесь на
положение двоичной запятой. Перед запятой должен стоять бит целой части
мантиссы, но поскольку она всегда равна 1, здесь данный бит не требуется и
соответствующий разряд отсутствует в памяти (но он подразумевается).
Значение порядка хранится здесь не как целое число, представленное в
дополнительном коде. Для упрощения вычислений и сравнения действительных
чисел значение порядка в ЭВМ хранится в виде смещенного числа, т.е. к
настоящему значению порядка перед записью его в память прибавляется
смещение. Смещение выбирается так, чтобы минимальному значению порядка
соответствовал нуль. Например, для типа Double порядок занимает 11 бит и
имеет диапазон от 2-1023 до 21023, поэтому смещение равно 1023(10) =
1111111111(2). Наконец, бит с номером 63 указывает на знак числа.
Таким образом, из вышесказанного вытекает следующий алгоритм для
получения представления действительного числа в памяти ЭВМ:
- перевести модуль данного числа в двоичную систему счисления;
- нормализовать двоичное число, т.е. записать в виде M × 2p, где M
мантисса (ее целая часть равна 1(2)) и p порядок, записанный в
десятичной системе счисления; - прибавить к порядку смещение и перевести смещенный порядок в двоичную
систему счисления; - учитывая знак заданного числа (0 положительное; 1 отрицательное),
выписать его представление в памяти ЭВМ.
Пример. Запишем код числа -312,3125.
- Двоичная запись модуля этого числа имеет вид 100111000,0101.
- Имеем 100111000,0101 =
1,001110000101 × 28. - Получаем смещенный порядок 8 + 1023 = 1031. Далее имеем
1031(10) = 10000000111(2). - Окончательно
1 10000000111 0011100001010000000000000000000000000000000000000000 63 62..52 51..0
Очевидно, что более компактно полученный код стоит записать следующим
образом: C073850000000000(16).
Другой пример иллюстрирует обратный переход от кода действительного
числа к самому числу.
Пример. Пусть дан код 3FEC600000000000(16) или
| 01111111110 | 1100011000000000000000000000000000000000000000000000 | |
| 63 | 62..52 | 51..0 |
- Прежде всего замечаем, что это код положительного числа, поскольку в
разряде с номером 63 записан нуль. Получим порядок этого числа:
01111111110(2) = 1022(10); 1022 — 1023 = -1. - Число имеет вид 1,1100011 × 2-1 или
0,11100011. - Переводом в десятичную систему счисления получаем 0,88671875.
Можно проверить себя:
Онлайн преобразователь для IEEE 754 чисел с двойной точностью
См. также стандарт IEEE 754
Контрольная работа по предсталению информации в памяти ЭВМ
А.П. Шестаков, 1999-2009
Сайт создан в системе uCoz
Представление чисел в компьютере
Существует несколько вариантов для отображения чисел в ЭВМ, и зависят они от формата числа.
Представление целых чисел в ЭВМ
Для представления целых чисел, в вычислительных машинах существует несколько способов, которые используют 8,16, 24 или 32 разряда памяти (1, 2, 3 и 4 байта).
Первым способом является беззнаковое представление. С его помощью представляются только целые положительные величины, которые не учувствуют в арифметических операциях и выступают в роли констант (дата, время и т.д.).
Чтобы представить число в беззнаковой форме необходимо перевести его в двоичную систему счисления и дополнить с начала нулями до нужной разрядности (дополняем до 1,2,3 или 4 байт).
Также следует отметить, что есть ограничения на количество чисел, которые можно представить в n разрядной ячейке. Для беззнаковых величин оно составляет \( 2^n \).

Пример: Перевести 54 в беззнаковый формат.
Находим представление 54 в бинарной системе счисления:
\( 1) \ 54:2 \ = \ 27 \ | \ Остаток \ 0 \)\( 2) \ 27:2 \ = \ 13 \ | \ Остаток \ 1 \)\( 3) \ 13:2 \ = \ 6 \ | \ Остаток \ 1 \)\( 4) \ 6:2 \ = \ 3 \ | \ Остаток \ 0 \)\( 5) \ 3:2 \ = \ 1 \ | \ Остаток \ 1 \)
Итого \( 54_{10} \) равняется \( 110110_{2} \).
Дополняем результат до одной из стандартных разрядностей (8 бит) = 00110110.
Ответ: 00110110.
Для представлениях чисел, которые учавствуют в вычислительных операциях, используется представление со знаком. В такой форме записи старший разряд всегда отводится под знак (0 для положительных чисел и 1 для отрицательных).
В случае со знаковым представлением также существуют ограничения. Так как один разряд отводится под знак, то в n-разрядную ячейку можно записать \( (2^{n-1} -1) \) положительных и \( 2^{n-1} \) отрицательных значений.
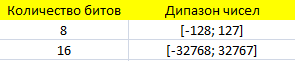
Также следует отметить следующую особенность — все отрицательные значения в компьютере хранятся в обратном или дополнительном коде, а положительные в прямом.
Для того чтобы перевести число в обратный и дополнительный код вам надо:
- Взять его значение по модулю и перевести в двоичную систему счисления (получим прямой код).
- Все нули заменить на 1, а единицы на нули (получаем обратный код).
- Для получения дополнительного кода прибавляем к нулевому разряду единицу.
Пример: Перевести -54 в дополнительный код.
- Из предыдущего примера — 54 в бинарной системе и беззнаковой форме равняется 00110110.
- Для получения обратного кода меняем 0 на 1, а 1 на 0 — 11001001.
- Чтобы получить дополнительный код прибавляем в конец единицу — 11001001 + 00000001 = 11001010.
Почему же для хранения отрицательных чисел используют обратный или дополнительный код? Это позволяет изменить операцию вычитания на операцию сложения. В противном случае компьютеру бы каждый раз приходилось выяснять, где положительная величина, а где отрицательная и после этого сравнивать их модули, для определения конечного знака, что очень сильно усложняло бы весь алгоритм.
Представление вещественных чисел
Всего существует два способа для представления множества вещественных значений – естественная или экспоненциальная форма.
В жизни мы пользуемся естественной формой. Так число 42,6 мы можем записать несколькими способами. Например:
- \( 426*10^{-1} \);
- \( 4,26*10^1 \);
- \( 42,6*10^0 \).
В компьютере же используется экспоненциальная форма записи. Выглядит она так:
Здесь m – мантисса, которая представляет собой правильную дробь (в правильных дробях числитель меньше знаменателя).
q – система счисления, в которой представлено число.
P – порядок.
В ЭВМ отводится один разряд под знак мантиссы, один под знак порядка и различное число бит под саму мантиссу и порядок. Данный формат записи называется «С плавающей запятой».
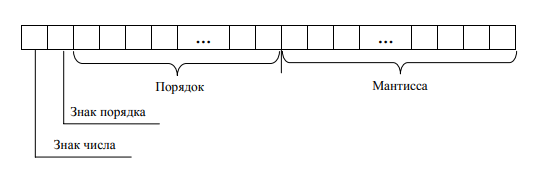
Чем больше бит отводится под мантиссу, тем точнее представляемая величина, чем больше ячеек отводится под порядок, тем шире диапазон от наименьшего числа, до наибольшего числа, представляемого в компьютере при заданном формате.
Так как компьютерная память величина дискретная и конечная, то и множество вещественных чисел, с которым работает ЭВМ также конечно.
Алгоритм представления числа с плавающей запятой.
- Перевести число из p-ичной системы счисления в двоичную;
- представить двоичное число в нормализованной экспоненциальной форме;
- рассчитать смещённый порядок числа;
- разместить знак, порядок и мантиссу в соответствующие разряды сетки.
Пример: Представить число -25,625 в машинном виде с использованием 4 байтового представления (где 1 бит отводится под знак числа, 8 бит – под смещённый порядок, остальные биты – под мантиссу).
2510=10001120,62510=0,1012-25,62510= -100011,10122. -100011,1012 = -1,000111012 * 2 4 3. СП=127+4=131 4.
Можно заметить, что представление действительного числа не очень удобно изображать в двоичной системе, поэтому часто используют шестнадцатеричное представление:
Окончательный ответ: C1CD0000.
Знаковое представление величины
Это представление также называется представлением «знак-величина» или «знак и величина». В этом подходе знак числа представлен в виде знаковый бит: установка этого кусочек (часто старший бит) на 0 для положительного числа или положительного нуля и установка на 1 для отрицательного числа или отрицательного нуля. Остальные биты в номере указывают величину (или абсолютная величина). Например, в восьмибитном байт, только семь битов представляют величину, которая может варьироваться от 0000000 (0) до 1111111 (127). Таким образом, числа в диапазоне от -12710 до +12710 может быть представлен после добавления знакового бита (восьмого бита). Например, −4310 закодировано в восьмибитном байте 10101011 а 4310 является 0101011. Использование представления величины со знаком имеет несколько последствий, что делает их более сложными для реализации:
- Есть два способа представить ноль: 00000000 (0) и 10000000 (−0).
- Сложение и вычитание требуют различного поведения в зависимости от знакового бита, в то время как одно дополнение может игнорировать знаковый бит и просто выполнять сквозной перенос, а два дополнения могут игнорировать знаковый бит и зависеть от поведения переполнения.
- Сравнение также требует проверки знакового бита, тогда как в дополнении до двух можно просто вычесть два числа и проверить, положительный или отрицательный результат.
- Минимальное отрицательное число -127 вместо -128 в случае дополнения до двух.
Этот подход напрямую сопоставим с обычным способом показа знака (размещение «+» или «-» рядом с величиной числа). Некоторые ранние бинарные компьютеры (например, IBM 7090) используют это представление, возможно, из-за его естественного отношения к обычному использованию. Знаковая величина — наиболее распространенный способ представления значимое в плавающая точка значения.
Другие системы
Существуют и другие базы подписанных цифр, такие как база . Ярким примером этого является кодирование Бута , в котором цифра установлена с помощью и , но используется основание . В стандартной двоичной системе счисления используются только цифры значения .
б ≠ б + + б — + 1 {\ displaystyle b \ neq b _ {+} + b _ {-} + 1} D знак равно { 1 ¯ , , 1 } {\ Displaystyle {\ mathcal {D}} = \ lbrace {\ bar {1}}, 0,1 \ rbrace} б + знак равно 1 {\ displaystyle b _ {+} = 1} б — знак равно 1 {\ displaystyle b _ {-} = 1} б знак равно 2 < 3 знак равно б + + б — + 1 {\ displaystyle b = 2 <3 = b _ {+} + b _ {-} + 1} { , 1 } {\ Displaystyle \ lbrace 0,1 \ rbrace}
Обратите внимание, что нестандартные представления цифр со знаком не уникальны. Например:
- 0111 D знак равно 4 + 2 + 1 знак равно 7 {\ displaystyle 0111 _ {\ mathcal {D}} = 4 + 2 + 1 = 7}
- 10 1 ¯ 1 D знак равно 8 — 2 + 1 знак равно 7 {\ displaystyle 10 {\ bar {1}} 1 _ {\ mathcal {D}} = 8-2 + 1 = 7}
- 1 1 ¯ 11 D знак равно 8 — 4 + 2 + 1 знак равно 7 {\ displaystyle 1 {\ bar {1}} 11 _ {\ mathcal {D}} = 8-4 + 2 + 1 = 7}
- 100 1 ¯ D знак равно 8 — 1 знак равно 7 {\ displaystyle 100 {\ bar {1}} _ {\ mathcal {D}} = 8-1 = 7}
Несмежная форма (НВС) кодирований Бута действительно гарантирует уникальное представление для каждого целого значения. Однако это применимо только к целочисленным значениям. Например, рассмотрим следующие числа в NAF:
- 2 3 знак равно 10 ¯ D знак равно 1. 1 ¯ ¯ D {\ displaystyle {\ frac {2} {3}} = 0. {\ overline {10}} _ {\ mathcal {D}} = 1. {\ overline {0 {\ bar {1}}}} _ { \ mathcal {D}}}
Общие сведения
Для кодирования информации используются различные формы представления данных. Это объясняется тем, что компьютер «не понимает» обыкновенного человеческого языка напрямую. Любая команда переводится в машинный код при помощи специальных алгоритмов кодирования данных. Чтобы в них разобраться, нужно освоить базовые понятия, к которым относятся следующие:

- Разрядная сетка.
- Виды СС.
- Перевод числовой информации на примере восьмеричной системы счисления.
https://youtube.com/watch?v=7Iy_jPXEedU
Разрядная сетка
Разрядной сеткой называется совокупность цифр, расположенных в определенном порядке значимости элементов. На первый взгляд, определение является сложным для понимания. Однако это не так. Чтобы в этом убедиться, необходимо разобрать число «126789». Оно состоит из компонентов, которые называются цифрами, где каждая принимает значение из диапазона от 0 до 9. Любая из них находится на определенном месте, а именно:

- 9 — единицы.
- 8 — десятки.
- 7 — сотни.
- 6 — тысячи.
- 2 — десятки тысяч.
- 1 — сотни тысяч.
Следует отметить, что значимость элементов определяется очень просто. Для этого нужно сравнить для примера сотни и единицы. Первые больше, чем вторые. На основании этого примера утверждение о значимости доказано.
https://youtube.com/watch?v=HdO3AbPdwio
Виды систем счисления
Системы счисления условно делятся на две группы. К ним относятся следующие:
- Позиционные.
- Унарные.
В первом случае расположение математических символов (цифр) играет важную роль, поскольку влияет на величину числа в целом. Чтобы в этом убедиться, нужно разобрать значение в десятичном формате 192. Для опыта необходимо переставить знаки. При этом получаются пять числовых величин:

- 921.
- 912.
- 219.
- 291.
- 129.
Следует отметить, что каждое из них отличается от другого. Все пять чисел можно также сравнить с исходным значением. Из выполненного опыта можно сделать вывод, что расположение компонентов в разрядной сетке имеет значение. К позиционным СС относятся следующие основные формы представления чисел:
- Двоичная.
- Восьмеричная.
- Шестнадцатеричная.
Однако существуют и другие формы представления числовых величин, а именно: третичная, четвертичная, пятеричная и т. д. Основным их отличием является основание.

Другим примером является подсчет количества мешков сахара, погруженных на грузовую машину. При загрузке одного мешка бригадир ставит обыкновенный произвольный символ, обозначающий единицу. У каждой системы счисления существует определенный алфавит или символы, используемые для записи цифр и чисел.
https://youtube.com/watch?v=x1bx7o2uESg
Двоичный код
Перед тем как начать работу с восьмеричным кодом нужно ознакомиться с двоичным. Чтобы перевести число из десятичной формы в двоичную, требуется воспользоваться следующим алгоритмом:

- Записать величину: 19.
- Поделить ее на двойку, обозначив остаток (1 — нацело не делится, 0 — целочисленное деление): 19/2=9 (в остатке 1).
- Поделить частное во втором пункте на 2: 9/2=4 (1).
- 4/2=2 (0).
- 2/2=1 (0).
- 1 — остаток
- Искомое значение (записывается снизу вверх): {2}.
Обратная операция выполняется по более упрощенной методике. Она имеет такой вид:
- Записать двоичный код: {2}.
- Умножить каждый его элемент на определенную степень, т. е. 1*2^4+0*2^3+0*2^2+1*2^1+1*2^0=19.
- Искомое значение: {2}.
Дополнительный код (дополнение до двух)[править]
Нумерация двоичных чисел в представлении c дополнением до двух.
Чаще всего для представления отрицательных чисел используется код с дополнением до двух (англ. Two’s complement).
Алгоритм получения дополнительного кода числа:
- если число неотрицательное, то в старший разряд записывается ноль, далее записывается само число;
- если число отрицательное, то все биты модуля числа инвертируются, то есть все единицы меняются на нули, а нули — на единицы, к инвертированному числу прибавляется единица, далее к результату дописывается знаковый разряд, равный единице.
В качестве примера переведём число в дополнительный восьмибитный код. Прямой код модуля : , обратный — , прибавляем , получаем , приписываем в качестве знакового разряда, в результате получаем .
Также дополнительный код отрицательного числа , хранящегося в битах, равен . По сути, дополнительный код представляет собой дополнение до : так как в -разрядной арифметике (двоичная запись этого числа состоит из единицы и нулей, а в -разрядную ячейку помещаются только младших разрядов, то есть нулей), то верно равенство .
Для получения из дополнительного кода самого числа нужно инвертировать все разряды кода и прибавить к нему единицу. Можно проверить правильность, сложив дополнительный код с самим числом: результат должен быть равен . Переведём обратно. Инвертируем — , прибавляем , получаем — модуль исходного числа . Проверим: .
Можно получить диапазон значений .
Длинная арифметика для чисел, представленных с помощью кода с дополнением до двухправить
Дополнительный код также удобно использовать для вычислений в длинной арифметике, особенно для операций сложения и вычитания. Это операции удобно выполнять с числами одинаковой длины, поэтому в старшие разряды меньшего числа нужно поместить нули (если число положительно) или единицы (если число отрицательно). Тогда числа будут выглядеть следующим образом: в старших разрядах бесконечное число нулей (единиц), а в младших разрядах уже встречаются и нули, и единицы, которые кодируют само число, а не знак. Удобство заключается в том, что нам не обязательно проделывать операции сложения с каждой парой бит, если мы знаем, что на этом отрезке в числах стоят либо единицы, либо нули. Таким образом, на этом отрезке в получившемся числе тоже будут либо только единицы, либо только нули. Операцию сложения можно выполнить только один раз для старших битов, таким образом мы узнаем знак получившегося числа. Вычитание тоже выполняется просто: инвертируем число, прибавляем один и получаем это число с минусом, затем просто делаем сложение.
Однако умножение с числами, представленными дополнительным кодом, выполнять не всегда оптимально: алгоритм либо слишком медленный (наивный алгоритм работает за ), либо слишком сложный. Лучше для умножение использовать прямой код (бит под знак). Тогда можно числа перевести в десятичную систему счисления, выполнить быстрое преобразование Фурье за , затем перевести их обратно в двоичную. Обычно такой алгоритм работает быстрее, чем выполнение операции напрямую с двоичными числами. Для деления обычно тоже лучше использовать прямой код.
Достоинства представления чисел с помощью кода с дополнением до двухправить
- Возможность заменить арифметическую операцию вычитания операцией сложения и сделать операции сложения одинаковыми для знаковых и беззнаковых типов данных, что существенно упрощает архитектуру процессора и увеличивает его быстродействие.
- Нет проблемы двух нулей.
Недостатки представления чисел с помощью кода с дополнением до двухправить
Ряд положительных и отрицательных чисел несимметричен, но это не так важно: с помощью дополнительного кода выполнены гораздо более важные вещи, желаемые от способа представления целых чисел.
В отличие от сложения, числа в дополнительном коде нельзя сравнивать как беззнаковые, или вычитать без расширения разрядности.
Несмотря на недостатки, дополнение до двух в современных вычислительных системах используется чаще всего.