Электрический заряд и элементарные частицы. закон сохранения заряда

Потенциал электрического поля. Разность потенциалов

Потенциал – скалярная физическая величина, равная отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда.

Обозначение – \( \varphi \), единица измерения в СИ – вольт (В).

Потенциал \( \varphi \) является энергетической характеристикой электростатического поля.

Разность потенциалов численно равна работе, которую совершает электрическая сила при перемещении единичного положительного заряда между двумя точками поля:

Обозначение – \( \Delta\varphi \), единица измерения в СИ – вольт (В).

Иногда разность потенциалов обозначают буквой \( U \) и называют напряжением.

Важно!
Разность потенциалов \( \Delta\varphi=\varphi_1-\varphi_2 \), а не изменение потенциала \( \Delta\varphi=\varphi_2-\varphi_1 \). Тогда работа электростатического поля равна:. Важно!
Эта формула позволяет вычислить работу электростатических сил в любом поле

В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки

Важно!
Эта формула позволяет вычислить работу электростатических сил в любом поле. В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки. В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность

В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность

В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки. В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Потенциал поля точечного заряда \( q \) в точке, удаленной от него на расстояние \( r \), вычисляется по формуле:

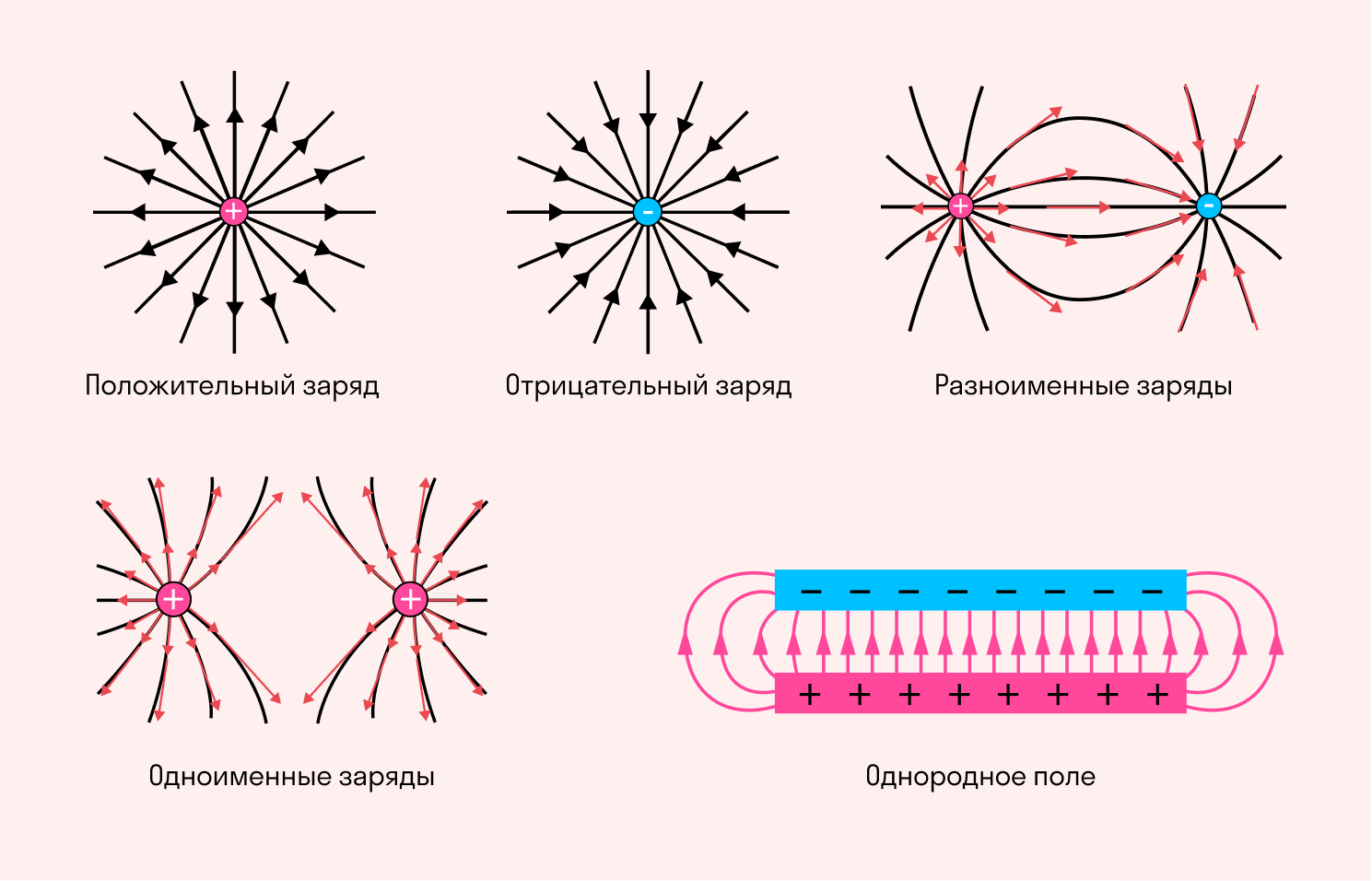
Для наглядного представления электрического поля используют эквипотенциальные поверхности.

Важно!
Внутри проводящего шара потенциал всех точек внутри шара равен потенциалу поверхности шара и вычисляется по формуле потенциала точечного заряда (\( r =R \), где \( R \) – радиус шара). Напряженность поля внутри шара равна нулю. Эквипотенциальной поверхностью, или поверхностью равного потенциала, называется поверхность, во всех точках которой потенциал имеет одинаковое значение

Эквипотенциальной поверхностью, или поверхностью равного потенциала, называется поверхность, во всех точках которой потенциал имеет одинаковое значение.

Свойства эквипотенциальных поверхностей

Вектор напряженности перпендикулярен эквипотенциальным поверхностям и направлен в сторону убывания потенциала.
Работа по перемещению заряда по эквипотенциальной поверхности равна нулю.

В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей. Для точечного заряда эквипотенциальные поверхности представляют собой концентрические окружности.

Разность потенциалов и напряженность связаны формулой:

Из принципа суперпозиции полей следует принцип суперпозиции потенциалов:

Потенциал результирующего поля равен сумме потенциалов полей отдельных зарядов.

Важно!
Потенциалы складываются алгебраически, а напряженности – по правилу сложения векторов. Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил. Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил

Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил.

Алгоритм решения таких задач:

установить характер и особенности электростатических взаимодействий объектов системы;
ввести характеристики (силовые и энергетические) этих взаимодействий, сделать рисунок;
записать законы сохранения и движения для объектов;
выразить энергию электростатического взаимодействия через заряды, потенциалы, напряженности;
составить систему уравнений и решить ее относительно искомой величины;
проверить решение.

Линии напряженности

Электрическое поле нельзя увидеть невооруженным глазом, но можно изобразить с помощью линий напряженности. Графически это будут непрерывные прямые, которые связывают заряженные объекты. Условная точка начала такой прямой — на положительном заряде, а конечная точка — на отрицательном.

Линии напряженности — это прямые, которые совпадают с силовыми линиями в системе из положительного и отрицательного зарядов. Касательные к ним в каждой точке электрического поля имеют то же направление, что и напряженность этого поля.

При графическом изображении силовых линий можно передать не только направление, но и величину напряженности электрического поля (разумеется, условно). В местах, где модуль напряженности выше, принято делать более густой рисунок линий. Есть и случаи, когда густота линий не меняется — это бывает при изображении однородного поля.

Однородное электрическое поле создается разноименными зарядами с одинаковым модулем, расположенными на двух металлических пластинах. Линии напряженности между этими зарядами представляют собой параллельные прямые всюду, за исключением краев пластин и пространства за ними.

Кулоновская сила

Концепция Кулона характеризует взаимодействие между двумя зарядами, пребывающими в состоянии покоя. Она гласит: два недвижимых заряда отталкивают либо притягивают один другого с силой, которая прямо пропорциональна произведению величин зарядов, но обратна длине расстояния между этими зарядами во второй степени. Вместе с этим, сила взаимодействия пары зарядов не может измениться при присутствии третьего.

С помощью кулоновского принципа естествоиспытатель может отыскать состояние равновесия в ситуации свободного перемещения зарядов под воздействием силы другого типа, при котором заряды будут распределяться с постоянным коэффициентом. Сила Кулона предопределена третьим законом Ньютона, который утверждает, что заряды воздействуют один на другого с силами, которые равны по модулям, но противоположны по направлениям.

Суперпозиция полей

Закон Кулона и все вытекающие из него утверждения являются лишь основой для другого, более масштабного принципа – закона суперпозиции. Исходя из этого фундаментального утверждения, силы, которые действуют на заряды, каждый из которых располагается в конкретной точке объединённой системы, являют собой сумму сил, имеющих строгое направление и формируемых отдельными группами зарядов по отдельности и влияющих на заряды в конкретных точках.

Принцип суперпозиции полей

В отличие от закона Кулона, принцип суперпозиции может быть недостаточным в рамках некоторых квантовых явлений в электрическом поле.

Формула заряда конденсатора, q

По назначению конденсатор можно сравнить с батарейкой. Но имеется принципиальное отличие в работе данных элементов. Существуют отличия в предельной емкости и скорости зарядки конденсатора и батарейки.

Формула заряда конденсатора

Величина заряда конденсатора (q) связана с его емкостью (C) и разностью потенциалов (U) между его обкладками как:

где q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками.

Электроемкость конденсатора — это величина, которая зависит то размеров и устройства конденсатора.

Заряд на пластинах плоского конденсатора равен:

где – электрическая постоянная; – площадь каждой (или наименьшей) пластины; – расстояние между пластинами; – диэлектрическая проницаемость диэлектрика, который находится между пластинами конденсатора.

Заряд на обкладках цилиндрического конденсатора вычисляется при помощи формулы:

где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.

Заряд на обкладках сферического конденсатора найдем как:

где – радиусы обкладок конденсатора.

Заряд конденсатора связан с энергией поля (W) внутри него:

Из формулы (6) следует, что заряд можно выразить как:

Рассмотрим последовательное соединение из N конденсаторов ( рис. 1).

Здесь (рис.1) положительная обкладка одного конденсатора соединяется с отрицательной обкладкой следующего конденсатора. При таком соединении, обкладки соседних конденсаторов создают единый проводник. У всех конденсаторов, соединенных последовательно на обкладках имеются равные по величине заряды.

При параллельном соединении конденсаторов (рис.2), соединяют обкладки, имеющие заряды одного знака. Суммарный заряд соединения (q) равен сумме зарядов конденсаторов.

Электрическое поле (к задачнику Рымкевича для 10-11 классов)

Электрическое поле к задачнику по физике за 10-11 классы «Физика. 10-11 класс. Пособие для общеобразовательных учебных заведений» Рымкевич А.П.

Электрическое поле и электрический заряд — первичные понятия, которые не определяются аналогично понятиям точки и прямой в геометрии. Неподвижный заряд создает вокруг себя электрическое поле. Если замкнутая система обладала зарядом q, то при любых изменениях в ней заряд q сохраняется. Это фундаментальное утверждение носит название закона сохранения заряда.

Точечным зарядом называется заряд исчезающе малых размеров. Из эксперимента известно, что два точечных заряда q1 и q2 на расстоянии r взаимодействуют с силой F, значение которой определяется законом Кулона:

где

— коэффициент пропорциональности. Когда заряды одноименные, то они отталкиваются, когда разноименные — притягиваются.

Силовой характеристикой электрического поля является вектор напряженности E;. Рассмотрим некоторый заряд q, внесенный в электрическое поле E;. Тогда на него будет действовать сила F;, которая определяется формулой: F; = qE;. Это формула может служить определением вектора напряженности электрического поля. Для графического представления электростатического поля пользуются понятием линий напряженности. Эти линии начинаются на положительных зарядах и заканчиваются на отрицательных. Касательная в каждой точке линии напряженности направлена также, как и вектор E; . Если имеется N зарядов, каждый из которых создает свое поле E1;, E2;,…, EN; , то полная напряженность в любой точке пространства E; определяется как векторная сумма этих напряженностей (принцип суперпозиции):

Для точечного заряда q значение напряженности E в точке, удаленной от него на расстоянии r, выражается формулой:

Проводником называется тело, содержащее свободные заряды. Если мы сообщим проводнику некоторый заряд q, то он распределится по поверхности, а внутри проводника поле будет равно нулю. Поверхностной плотностью о называется отношение заряда к площади поверхности проводника

Поле заряженного проводящего шара снаружи от него совпадает с полем точечного заряда, а внутри него равно нулю. Поле бесконечной заряженной проводящей плоскости с поверхностной плотностью заряда о определяется формулой:

где ε0 = 8,854⋅10-12 Ф/м — электрическая постоянная.

Диэлектриком называется тело, в котором отсутствуют свободные заряды. При помещении диэлектрика в электрическое поле происходит его поляризация, при этом поле E в диэлектрике уменьшается в ε раз:

где E0 — напряженность поля вне диэлектрика, ε — диэлектрическая проницаемость. При перемещении заряда q в электрическом поле E; на

расстояние

совершается работа A:

Изменение потенциальной энергии ΔWP равно:

Потенциал φ — энергетическая характеристика электрического поля, он определяется формулой:

Эквипотенциальные поверхности — это такие поверхности, в каждой точке которых потенциал постоянен. Потенциал поля φ в некоторой точке пространства, созданный N зарядами, равен алгебраической сумме потенциалов φ1, φ2,…, φN созданных отдельными зарядами (принцип суперпозиции): φ = φ1 + φ2 + … +

φN- Потенциал поля точечного заряда q на расстоянии r от него определяется формулой:

Напряжением U между точками A и B называется разность потенциалов:

где φ1 — потенциал в точке A, φ2 — потенциал в точке B. Напряжение U связано с напряженностью E электрического поля следующей формулой:

Конденсатором называется устройство, способное накапливать заряд. Емкость конденсатора C определяется как отношение заряда q на его обкладках к приложенному напряжению U:

Емкость не зависит от заряда и напряжения на нем, а определяется его геометрическими свойствами (формой и размером) и родом среды. Для плоского конденсатора емкость равна:

где ε — диэлектрическая проницаемость среды между обкладками, S — площадь обкладок, d — расстояние между обкладками. Энергия заряженного конденсатора W определяется формулой:

Плотность энергии ω электрического поля E выражается формулой:

Закон сохранения электрического заряда. Закон Кулона

Подробности: Просмотров: 654

Электродинамика — наука о свойствах электромагнитного поля.Электромагнитное поле — определяется движением и взаимодействием заряженных частиц.Проявление эл/магнитного поля — это действие эл/магнитных сил:
1) силы трения и силы упругости в макромире;
2) действие эл/магнитных сил в микромире (строение атома, сцепление атомов в молекулы, превращение элементарных частиц)Открытие эл/магнитного поля — Дж. Максвелл.

ЭЛЕКТРОСТАТИКА

— раздел электродинамики, изучает покоящиеся электрически заряженные тела.Элементарные частицы могут иметь эл. заряд, тогда они называются заряженными;
— взаимодействуют друг с другом с силами, которые зависят от расстояния между частицами, но превышают во много раз силы взаимного тяготения (это взаимодействие называется электромагнитным).Электрический заряд — физическая величина, определяет интенсивность электромагнитных взаимодействий.
Существует 2 знака эл.зарядов: положительный и отрицательный.
Частицы с одноименными зарядами отталкиваются, с разноименными — притягиваются.
Протон имеет положительный заряд, электрон — отрицательный, нейтрон — электрически нейтрален.Элементарный заряд — минимальный заряд, разделить который невозможно.
Чем объяснить наличие электромагнитных сил в природе? — в состав всех тел входят заряженные частицы.
В обычном состоянии тела электрически нейтральны (т.к. атом нейтрален), и электромагнитные силы не проявляются.Тело заряжено, если имеет избыток зарядов какого-либо знака:
отрицательно заряжено — если избыток электронов;
положительно заряжено — если недостаток электронов.Электризация тел — это один из способов получения заряженных тел, например, соприкосновением).
При этом оба тела заряжаются , причем заряды противоположны по знаку, но равны по модулю.

Закон сохранения электрического заряда

В замкнутой системе алгебраическая сумма зарядов всех частиц остается неизменной.
( … но, не числа заряженных частиц, т.к. существуют превращения элементарных частиц).

Замкнутая система- система частиц, в которую не входят извне и не выходят наружу заряженные частицы.

Закон Кулона — основной закон электростатики.

Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей заряда и обратно пропорциональна квадрату расстояния между ними.
Когда тела считаются точечными? — если расстояние между ними во много раз больше размеров тел.
Если у двух тел есть электрические заряды, то они взаимодействуют по закону Кулона.Единица электрического заряда: 1 Кл — это заряд, проходящий за 1 секунду через поперечное сечение проводника при силе тока 1 А.
1 Кл — очень большой заряд. Элементарный заряд:

Коэффициент пропорциональности

Принято записывать коэффициент пропорциональности в законе Кулона в вакууме в виде

где электрическая постоянная

Закон Кулона для величины силы взаимодействия зарядов в произвольной среде (в СИ):

Диэлектрическая проницаемость среды характеризует электрические свойства среды. В вакууме

Таким образом, сила Кулона зависит от свойств среды между заряженными телами.

Следующая страница «Близкодействие и дальнодействие. Электрическое поле. Напряженность электрического поля. Принцип суперпозиции полей. Силовые линии электрического поля»

Назад в раздел «10-11 класс»

Электростатика и законы постоянного тока — Класс!ная физика

Электрический заряд. Электризация. Закон сохранения электрического заряда. Закон Кулона. Единица электрического заряда —
Близкодействие и дальнодействие. Электрическое поле. Напряженность электрического поля. Принцип суперпозиции полей. Силовые линии электрического поля —
Проводники и диэлектрики в электростатическом поле. Поляризация диэлектриков —
Потенциальная энергия тела в электростатическом поле. Потенциал электростатического поля и разность потенциалов. Связь между напряженностью электростатического поля и разхностью потенциалов —
Электроемкость. Конденсаторы. Энергия заряженного конденсатора —
Электрический ток. Сила тока. Условия, необходимые для существования электрического тока. Закон Ома для участка цепи. Сопротивление —
Работа и мощность тока

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Если массивную гирю поставить на пластину из изолятора и соединить с электрометром, а затем несколько раз ударить по ней куском меха, то гиря приобретёт отрицательный заряд и стрелка электрометра отклонится. При этом кусок меха приобретёт заряд

1) равный нулю
2) положительный, равный по модулю заряду гири
3) отрицательный, равный заряду гири
4) положительный, больший по модулю заряда гири

2. Два точечных заряда будут притягиваться друг к другу, если заряды

1) одинаковы по знаку и любые по модулю
2) одинаковы по знаку и обязательно одинаковы по модулю
3) различны по знаку, но обязательно одинаковы по модулю
4) различны по знаку и любые по модулю

3. На рисунках изображены три пары одинаковых лёгких заряженных шариков, подвешенных на шёлковых нитях. Заряд одного из шариков указан на рисунках. В каком(-их) случае(-ях) заряд второго шарика может быть отрицателен?

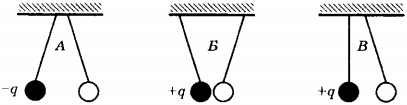
1) только А
2) А и Б
3) только В
4) А и В

4. Ученик во время опыта по изучению взаимодействия металлического шарика, подвешенного на шёлковой нити, с положительно заряженным пластмассовым шариком, расположенным на изолирующей стойке, зарисовал в тетради наблюдаемое явление: нить с шариком отклонилась от вертикали на угол \( \alpha \). На основании рисунка можно утверждать,что металлический шарик

1) имеет положительный заряд
2) имеет отрицательный заряд
3) не заряжен
4) либо не заряжен, либо имеет отрицательный заряд

5. Отрицательно заряженное тело отталкивает подвешенный на нити лёгкий шарик из алюминиевой фольги. Заряд шарика:

A. положителен
Б. отрицателен
B. равен нулю

Верными являются утверждения:

1) только Б
2) Б и В
3) А и В
4) только В

6. Металлический шарик 1, укреплённый на длинной изолирующей ручке и имеющий заряд \( +q \), приводят поочерёдно в соприкосновение с двумя такими же изолированными незаряженными шариками 2 и 3, расположенными на изолирующих подставках.

Какой заряд в результате приобретёт шарик 2?

1) 0
2) \( \frac{q}{4} \)
3) \( \frac{q}{3} \)
4) \( \frac{q}{2} \)

7. От капли, имеющей электрический заряд \( -2e \), отделилась капля с зарядом \( +e \). Каков электрический заряд оставшейся части капли?

1) \( -e \)
2) \( -3e \)
3) \( +e \)
4) \( +3e \)

8. Металлическая пластина, имевшая отрицательный заряд \( -10e \), при освещении потеряла четыре электрона. Каким стал заряд пластины?

1) \( +6e \)
2) \( +14e \)
3) \( -6e \)
4) \( -14e \)

9. К водяной капле, имевшей электрический заряд \( +5e \) присоединилась кайля с зарядом \( -6e \). Каким станет заряд объединенной капли?

1) \( +e \)
2) \( -e \)
3) \( +11e \)
4) \( -11e \)

10. На рисунке изображены точечные заряженные тела. Тела А и Б имеют одинаковый отрицательный заряд, а тело В равный им по модулю положительный заряд. Каковы модуль и направление равнодействующей силы, действующей на заряд Б со стороны зарядов А и В?

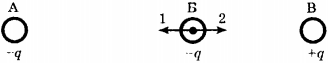
1) \( F=F_А+А_В \); направление 2
2) \( F=F_А-А_В \); направление 2
3) \( F=F_А+А_В \); направление 1
4) \( F=F_А-А_В \); направление 1

11. Из перечня приведённых ниже высказываний выберите два правильных и запишите их номера в таблицу.

1) Сила взаимодействия между электрическими зарядами тем больше, чем больше расстояние между ними.
2) При электризации трением двух тел их суммарный заряд равен нулю.
3) Сила взаимодействия между электрическими зарядами тем больше, чем больше заряды.
4) При соединении двух заряженных тел их общий заряд будет меньше, чем алгебраическая сумма их зарядов до соединения.
5) При трении эбонитовой палочки о мех заряд приобретает только эбонитовая палочка.

12. В процессе трения о шёлк стеклянная линейка приобрела положительный заряд. Как при этом изменилось количество заряженных частиц на линейке и шёлке при условии, что обмен атомами при трении не происходил? Установите соответствие между физическими величинами и их возможными изменениями при этом. Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) количество протонов на шёлке
Б) количество протонов на стеклянной линейке
B) количество электронов на шёлке

ХАРАКТЕР ИЗМЕНЕНИЯ
1) увеличилась
2) уменьшилась
3) не изменилась

Потенциал. Эквипотенциальные поверхности.

В механике взаимодействие тел характеризует силой или потенциальной энергией. Электрическое поле, которое обеспечивает взаимодействие между электрически заряженными телами, также характеризуют двумя величинами. Напряженность электрического поля — это силовая характеристика. Теперь введем энергетическую характеристику — потенциал. С помощью этой величины можно будет сравнивать между собой любые точки электрического поля. Таким образом, потенциал как характеристика поля должен зависеть от значения заряда, содержащегося в этих точках. Поделим обе части формулы A = W₁ — W₂ на заряд q, получим

Отношение W/q не зависит от значения заряда и принимается за энергетическую характеристику, которую называют потенциалом поля в данной точке. Обозначают потенциал буквой φ.

Потенциал электрического поля φ — скалярная энергетическая характеристика поля, которая определяется отношением потенциальной энергии W положительного заряда q в данной точке поля к величине этого заряда:

Единица потенциала — вольт:

Подобно потенциальной энергии значения потенциала в данной точке зависит от выбора нулевого уровня для отсчета потенциала. Чаще всего в электродинамике за нулевой уровень берут потенциал точки, лежащей в бесконечности, а в электротехнике — на поверхности Земли.

С введением потенциала формулу для определения работы по перемещению заряда между точками 1 и 2 можно записать в виде

Поскольку при перемещении положительного заряда в направлении вектора напряженности электрическое поле выполняет положительную работу A = q (φ₁ — φ₂ )> 0, то потенциал φ₁ больше чем потенциал φ₂ . Таким образом, напряженность электрического поля направлена в сторону уменьшения потенциала.

Если заряд перемещать с определенной точки поля в бесконечность, то работа A = q (φ — φ_∞ ). Поскольку φ_∞ = 0, то A = qφ. Таким образом, величина потенциала φ определенной точки поля определяется работой, которую выполняет электрическое поле, перемещая единичный положительный заряд из этой точки в бесконечность,

Если электрическое поле создается точечным зарядом q, то в точке, лежащей на расстоянии r от него, потенциал вычисляют по формуле

По этой формуле рассчитывают и потенциал поля заряженного шара. В таком случае r — это расстояние от центра шара до выбранной точки поля. С этой формулы видно, что на одинаковых расстояниях от точечного заряда, который создает поле, потенциал одинаков. Все эти точки лежат на поверхности сферы, описанной радиусом r вокруг точечного заряда. Такую сферу называют эквипотенциальной поверхностью.

Эквипотенциальные поверхности — геометрическое место точек в электрическом поле, которые имеют одинаковый потенциал, — один из методов наглядного изображения электрических полей.

Эквипотенциальные поверхности электрических полей, созданных точечными зарядами разных знаков

Силовые линии всегда перпендикулярны эквипотенциальных поверхностей. Это означает, что работа сил поля по перемещению заряда по эквипотенциальной поверхности равна нулю.

В случае наложения электрических полей, созданных несколькими зарядами, потенциал электрического поля равен алгебраической сумме потенциалов полей, созданных отдельными зарядами, φ = φ₁ + φ₂ + φ₃ . Эквипотенциальные поверхности таких систем имеют сложную форму. Например, для системы из двух одинаковых по значению одноименных зарядов эквипотенциальные поверхности имеют вид, изображенный на рисунке. Эквипотенциальные поверхности однородного поля явлются плоскостями.

Эквипотенциальные поверхности: а — поля двух одинаковых зарядов б — однородного поля

Закон кулона, определение и формула