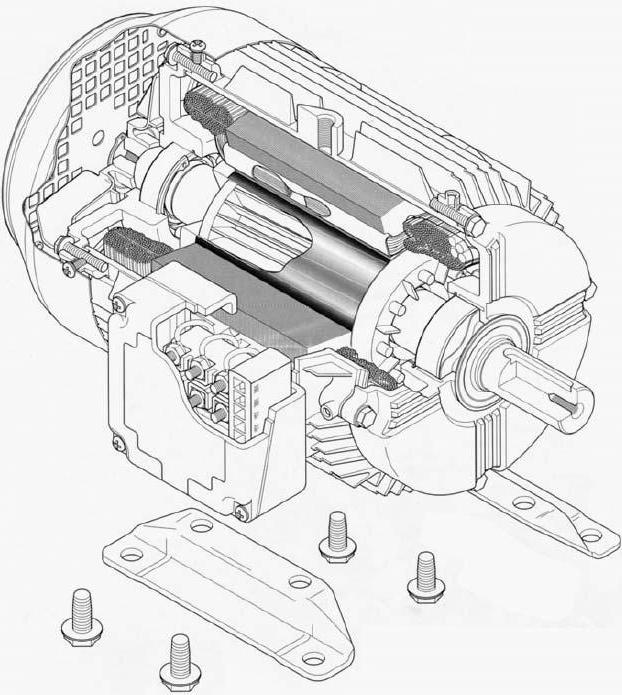
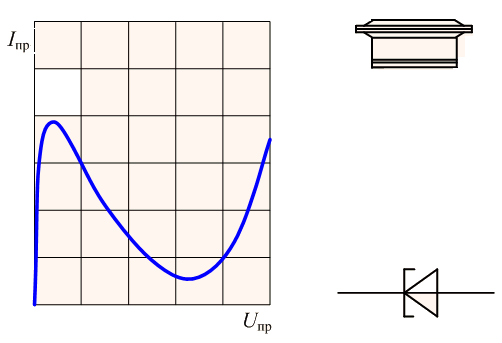
↑ Печатная плата
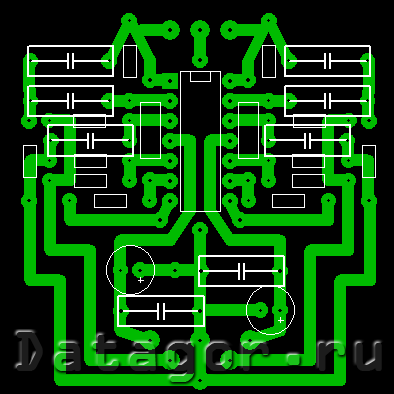
В качестве ОУ я применил счетверенный ОУ типа К1401УД2. Эта плата под него. Для стереосистемы из двух двухполосных АС достаточно собрать 1 плату.
#09/02/2021
Печатка От Игоря (Datagor) под LM324, LM2902, LM224, LM124:
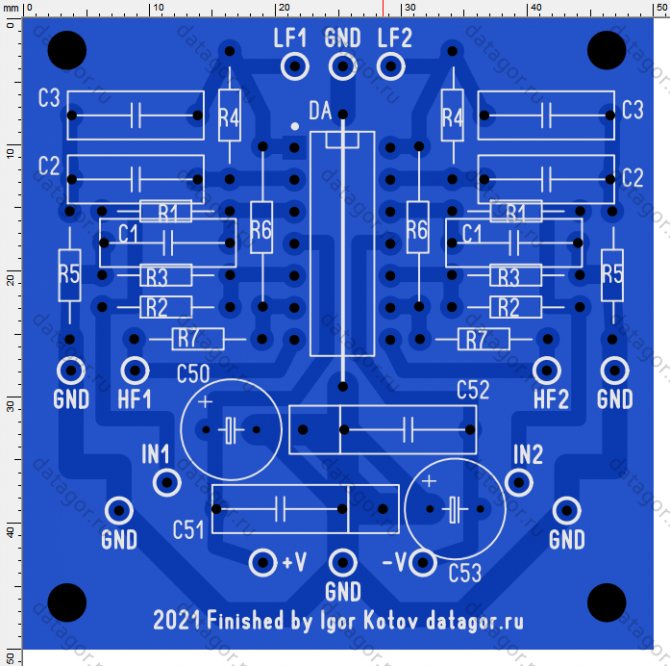
Причесал ПП, изменил питание под импортные ОУ (!), подписал компоненты согласно схеме, подписал входы и выходы и т.п. GND — общий питания, земля; +V, −V — питание ±12V … 15V; IN1, IN2 — аудиовходы (ЛК, ПК) от источника (зв.карта, ЦАП, пред, телефон); HF1, HF2 — выходы ВЧ-полос, на усилители; LF1, LF2 — выходы НЧ-полос, на усилители; Конденсаторы по питанию, которых нет на схеме: С50, С53 — 100μF … 470μF 16V (электролит); С51, С52 — 0.1μF … 0.68μF (плёнка или керамика); ОУ — LM324, LM2902, LM224, LM124 и др, счетверённые (dip-14 quadruple opamp).
Обратите внимание:
у импортных ОУ и у К1401УД2 питание инверсное! Шутка отечественных разработчиков. Выбирайте ПП соответственно вашему ОУ.
Забирайте ПП в файлах.
Что такое полосовой фильтр
Как следует из названия, полосовой фильтр фильтрует все частоты, пропуская только частоты, находящиеся в определенном диапазоне. Все частоты за пределами данного частотного диапазона ослабляются.
Есть два основных параметра определяющие характеристики полосового фильтра: полоса пропускания, где фильтр пропускает сигналы и полоса затухания, в которой сигналы ослабляются.
Идеальный полосовой фильтр имеет ровную полосу пропускания (усиление и отсутствие затухания сигнала по всей полосе пропускания) и полное затухание вне полосы пропускания. Кроме того, переход из полосы пропускания абсолютно резкий.
Тестер транзисторов / ESR-метр / генератор
Многофункциональный прибор для проверки транзисторов, диодов, тиристоров…
Подробнее
Но на практике невозможно создать идеальный полосовой фильтр. Реальный фильтр неспособен полностью задержать все частоты за границами желаемого диапазона частот. В частности, имеется область в непосредственной близости у границы заданного диапазона, где сигнал частично ослабляется, но не отфильтровывается полностью. Эта область носит название крутизна спада фильтра, и измеряется в дБ затухания на октаву. Как правило, при проектировании, стремятся сделать данный спад как можно более узким, что позволяет получить фильтр максимально приближенным к заданным параметрам.
Фильтр для усилителя PAM8403
В статье я не буду открывать никакой Америки. Однако, представленную ниже информацию в нужном контексте в Интернете я не нашел и решил это исправить.
История вот в чем. Есть у меня некоторое количество модулей усилителей класса D на базе микросхем PAM8403. Это, наверное, самая популярная и дешевая микросхема усилителей, которая применяется в море DIY самоделок. Но звучит она, мягко говоря, так себе. Тем не менее, у меня есть предложение, как сделать её лучше.
Причиной этих мыслей стало применение такой микросхемы в качестве колонки, которая подключена к моему компу и я слушаю через неё музычку. Городить что-то сложнее нет желания, но страдать от звука тоже не хочется. С предисловием закончили, переходим к практике.
Для начала, давайте подключим к усилителю динамик 8 Ом 1 Вт и посмотрим на сигнал на выходе
Тут важно помнить, что микросхема имеет мостовую схему выхода, поэтому нельзя соединять минус выхода и землю. Все измерения я проводил на реальном динамике, а не на резистивной нагрузке
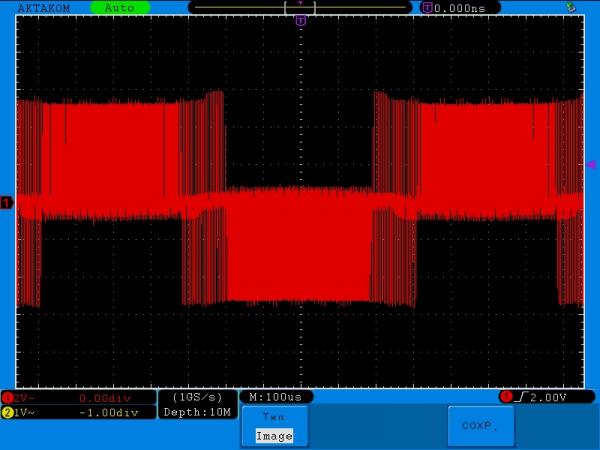
Вы видите синус 1 кГц? Вот и я не вижу, а он есть. Понятное дело, что это D класс и «китайцы», в силу удешевления и простоты, не стали заморачиваться с выходными фильтрами, чтобы подавлять ВЧ импульсы, и просто написали в описании микросхемы:
Оно-то как бы работает, но что-то из ушей вытекает все-таки… Собственно, предлагаемая мной доработка представляет собой LC фильтр по следующей топологии. Я использую только один канал, если вы хотите такое для стерео, то надо собрать два таких фильтра.
Берем две индуктивности и пару конденсаторов. Значение индуктивности должно быть от 10 до 50 мкГн, конденсаторы должны быть от 0.22 до 1 мкФ. В моем случае я раздобыл пару колец T94-2 и намотал на них около 47 витков проводом от витой пары, что должно было дать примерно 20 мкГн, конденсаторы по 0.47 мкФ. Как-то так это выглядит.

А теперь немного измерений. Сначала спектр с шагом 1 кГц и 10 кГц при выключенном входном сигнале. Шаг по амплитуде (вертикали) 20 дБ.
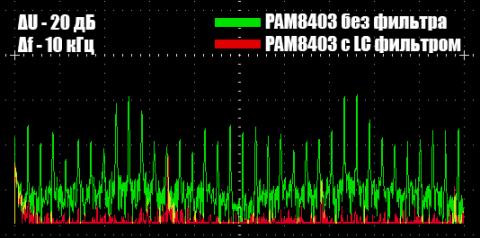
А теперь синус в 1 кГц. Шаг по частоте и амплитуде аналогичен предыдущим картинкам.
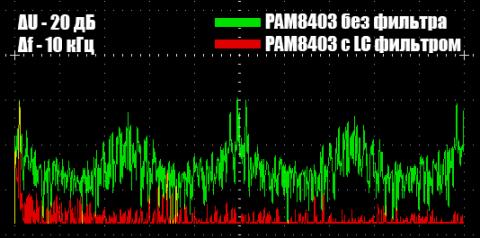
Фильтр уменьшает уровень шума на 20 дБ.
Теперь подаем немного шума, дабы примерно понять АЧХ получившегося фильтра. Здесь шаг по частоте 5 кГц, по амплитуде по прежнему 20 дБ.
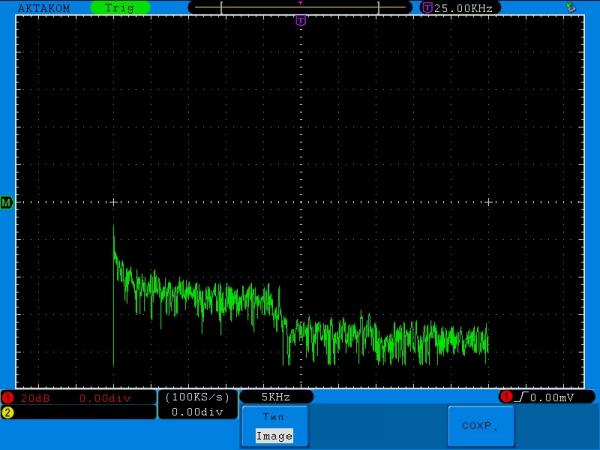
Получился спад примерно на 23 кГц, что меня вполне устраивает. Хотя, тут, безусловно, существует влияние цепей аудиовыхода компьютера. Ну и помните мнимый синус в 1 кГц? Теперь он выглядит так.
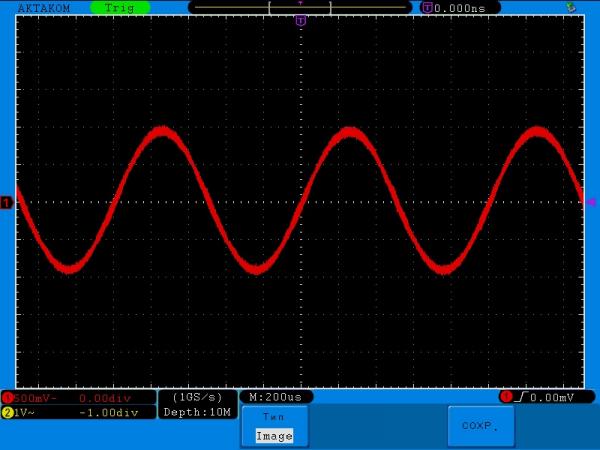
Теперь мой мозг не вытекает от высокочастотного шума из колонки. При питании от USB советую добавить еще по питанию LC фильтр. Но не переборщите с емкостью конденсатора, иначе чего-нибудь да сгорит. И еще совет. Подавайте звук на усилитель через переменный резистор. Лучше держать громкость на компьютере на высоком уровне и регулировать её резистором. Таким образом вы увеличите соотношение сигнал-шум и уменьшите цифровой шум, который в любом случае будет проникать в сигнал. У меня получилась следующая схема подключения.
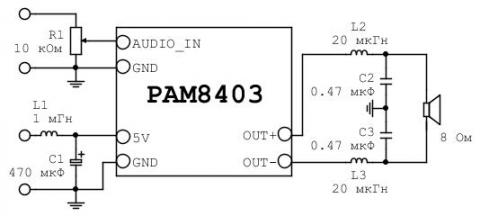
Надеюсь, статья будет кому-нибудь полезна. Крепкого всем здоровья. И слушайте музыку, а не усилители.
Калькулятор простых фильтров: https://sim.okawa-denshi.jp/en/Fkeisan.htm
Список радиоэлементов
| Обозначение | Тип | Номинал | Количество | Примечание | Магазин | Мой блокнот |
| Микросхема | PAM8403 | 1 | Поиск в магазине Отрон | В блокнот | ||
| L1 | Катушка индуктивности | 1 мГн | 1 | фильтр USB | Поиск в магазине Отрон | В блокнот |
| L2, L3 | Катушка индуктивности | 20 мкГн | 2 | для одного канала | Поиск в магазине Отрон | В блокнот |
| C1 | Конденсатор | 470 мкФ | 1 | фильтр USB | Поиск в магазине Отрон | В блокнот |
| C2, C3 | Конденсатор | 0.47 мкФ | 2 | для одного канала | Поиск в магазине Отрон | В блокнот |
| R1 | Переменный резистор | 10 кОм | 1 | Поиск в магазине Отрон | В блокнот | |
| Добавить все |
Фазовый сдвиг фильтра низких частот
До сих пор мы обсуждали способ, которым фильтр изменяет амплитуду различных частотных составляющих в сигнале. Однако реактивные элементы цепи в дополнение к влиянию на амплитуду всегда вносят сдвиг фазы.
Понятие фазы относится к значению периодического сигнала в определенный момент цикла. Таким образом, когда мы говорим, что схема вызывает сдвиг фазы, то имеем в виду, что она создает смещение между входным и выходным сигналами: входной и выходной сигналы больше не начинают и заканчивают свои циклы в один и тот же момент времени. Значение сдвига фазы, например, 45° или 90°, показывает, какое было создано смещение.
Каждый реактивный элемент в цепи вводит сдвиг фазы на 90°, но этот фазовый сдвиг происходит не сразу. Фаза выходного сигнала, так же как и амплитуда выходного сигнала, изменяется постепенно по мере увеличения частоты входного сигнала. В RC фильтре нижних частот у нас есть один реактивный элемент (конденсатор), и, следовательно, схема в конечном итоге будет вводить сдвиг фазы на 90°.
Как и в случае амплитудно-частотной характеристикой, фазо-частотную характеристику легче всего оценить, изучив график, на котором частота на горизонтальной оси приведена в логарифмическом масштабе. Приведенное ниже описание дает общее представление, а затем вы можете заполнить детали, изучив график.
- Сдвиг фазы изначально равен 0°.
- Он постепенно увеличивается до достижения 45° на частоте среза; на этом участке характеристики скорость изменения увеличивается.
- После частоты среза сдвиг фазы продолжает увеличиваться, но скорость изменения уменьшается.
- Скорость изменения становится очень малой, когда сдвиг фазы асимптотически приближается к 90 °.
Рисунок 11 – Сплошная линия – это амплитудно-частотная характеристика, а пунктирная линия – это фазо-частотная характеристика. Частота среза составляет 100 кГц
Обратите внимание, что на частоте среза сдвиг фазы составляет 45°
Полосовые резонансные фильтры
Полосовые резонансные частотные фильтры – предназначены для выделения, или режекции (вырезания) определённой полосы частот. Резонансные частотные фильтры могут состоять из одного, двух, или трех колебательных контуров, настроенных на определённую частоту. Резонансные фильтры обладают наиболее крутым подъёмом (или спадом) АЧХ, по сравнению с другими (не резонансными) фильтрами. Полосовые резонансные частотные фильтры могут быть одноэлементными — с одним контуром, Г-образными – с двумя контурами, Т и П-образными – с тремя контурами, многозвенными – с четырьмя и более контурами.
На рисунке представлена схема Т-образного полосового резонансного фильтра, предназначенного для выделения определённой частоты. Состоит он из трёх колебательных контуров. CL и CL – последовательные колебательные контуры, на резонансной частоте имеют малое сопротивление протекающему току, а на других частотах наоборот – большое. Параллельный контур CL наоборот, имеет большое сопротивление на резонансной частоте, обладая малым сопротивлением на других частотах. Для расширения ширины полосы пропускания такого фильтра, уменьшают добротность контуров, изменяя конструкцию катушек индуктивности, расстраивая контура «вправо, влево» на частоту, немного отличающуюся от центральной резонансной, параллельно контуру CL подключают резистор.
На следующем рисунке представлена схема Т-образного режекторного резонансного фильтра, предназначенного для подавления определённой частоты. Он, как и предыдущий фильтр состоит из трёх колебательных контуров, но принцип выделения частот у такого фильтра другой. CL и CL – параллельные колебательные контуры, на резонансной частоте имеют большое сопротивление протекающему току, а на других частотах – маленькое. Параллельный контур CL наоборот, имеет малое сопротивление на резонансной частоте, обладая большим сопротивлением на других частотах. Таким образом, если предыдущий фильтр резонансную частоту выделяет, а остальные частоты подавляет, то этот фильтр, беспрепятственно пропускает все частоты, кроме резонансной частоты.
Порядок расчёта полосовых резонансных фильтров основан всё на том же делителе напряжения, где в качестве единичного элемента выступает LC контур с его характеристическим сопротивлением. Как рассчитывается колебательный контур, определяются его резонансная частота, добротность и характеристическое (волновое) сопротивление вы можете найти в статье Колебательный контур.
Электромагнитная совместимость частотных преобразователей
Электромагнитная совместимость технических средств — это нормальная (с требуемым качеством) работоспособность технического оборудования в реальной окружающей обстановке несмотря на непреднамеренное воздействие электромагнитных помех и способность не создавать недопустимых помех другой технике.
Все модели векторных преобразователей частоты оснащаются сетевыми фильтрами, чем обеспечивается необходимый уровень ЭМС. Фильтры допускается не применять в диапазоне до 30 кВт. Все преобразователи частоты большей мощности снабжаются встроенными фильтрами по умолчанию. Встроенный фильтр даёт возможность доводить до минимума наводки и помехи в электронной технике.
Область применения
Фильтр высокой частоты можно использовать для того, чтобы выделять высокочастотные сигналы. Также часто его применяют при обработке аудиосигналов, например, в раздельных фильтрах, которые еще называют кроссоверными. Также они используются для обрабатывания изображений, чтобы можно было осуществить преобразование в частотной области.
Вот из чего состоит простейший фильтр высоких частот:
- Резистор.
- Конденсатор.
Работа сопротивления на емкость (R х С) есть постоянной времени (длительность протекания процесса) для данного фильтра, которая будет обратно пропорциональна частоте среза в герцах (единица измерения процессов колебаний).
Фильтр на гираторах
В глубинах документации от Burr Brown был найден очень интересный документ AB-026. Он повествует о построении ими фильтров на гираторах для демонстрационных плат с ЦАП и АЦП.
Хорошая у них документация, не так давно у них же была найдена схема усилителя для наушников.
Ребята из Burr Brown рекомендуют применять для ЦАП фильтр на гираторе третьего порядка, а для АЦП фильтр на гираторах 6-го порядка.
В статье будет рассмотрен только фильтр третьего порядка. Ибо фильтр 6-го порядка это два фильтра третьего порядка включенные последовательно.
Схему фильтра мы рассмотрим чуть позже, а пока рассмотрим зачем это вообще нужно.
7.2.2. Пассивные LC-фильтры
LC-фильтры были первыми фильтрами, которые использовались в устройствах передачи сигналов.
Пассивный фильтр, реализующий характеристики Баттерворта или Чебышева, представляет лестничную LC-цепь, включенную между резистивным сопротивлением источника сигнала и нагрузкой (рис. 7.4). Элементы фильтра рассчитывают таким образом, чтобы обеспечить передачу максимальной мощности в полосе пропускания.
Рис. 7.4
С помощью лестничной LC-цепи можно реализовать только передаточные функции, нули передачи которых расположены на мнимой оси. Однако это не является серьезным ограничением, так как нули передачи частотно-селективных фильтров, как правило, расположены на мнимой оси, включая начало координат и бесконечность.
В простейшем случае нули передачи находятся в бесконечности. Таким свойством обладают передаточные функции фильтров нижних частот Баттерворта и Чебышева. Продольные ветви LC-цепи содержат индуктивности, а поперечные – емкости. Если нули передачи расположены в начале координат (фильтр верхних частот), то продольные ветви содержат емкостные элементы, а поперечные – индуктивные. Отличие фильтров Баттерворта и Чебышева в этом случае заключается только в разных значениях реактивных элементов, получаемых в процессе расчета. Количество реактивных элементов определяется порядком фильтра n.
Методы синтеза LC-фильтров хорошо разработаны. Существует обширная справочная литература, которая содержит данные о фильтрах различных порядков. Процедура расчета фильтра сводится к выбору типа и порядка фильтра.
Пассивные фильтры устойчивы, не требуют источников питания, имеют низкую чувствительность характеристик к изменениям номиналов элементов. Их основной недостаток при работе на частотах меньше 100 МГц – большие габариты и вес, обусловленные размерами индуктивных катушек.
В настоящее время во многих областях радиоэлектроники LC-фильтры почти вытеснены цифровыми и аналоговыми активнымиRC-фильтрами. Однако пассивные фильтры по-прежнему используются на частотах, превышающих 100 кГц.
Методы проектирования аналоговых фильтров с типовыми амплитудно-частотными характеристиками хорошо разработаны. Имеются многочисленные справочники, в которых приведены подробные таблицы с параметрами фильтров различных порядков. В табл. 7.1 и 7.2 приведены значения элементов нормированных фильтров Баттерворта и Чебышева с частотой среза 1 рад/с.
Таблица 7.2.1.
Значения элементов фильтров Баттерворта
|
n |
С1 |
L2 |
C3 |
L4 |
C5 |
L6 |
C7 |
L8 |
C9 |
|
2 |
1,4142 |
1,4142 |
|||||||
|
3 |
1,0000 |
2,0000 |
1,0000 |
||||||
|
4 |
0,7654 |
1,8478 |
1,8478 |
0,7654 |
|||||
|
5 |
0,6180 |
1,6180 |
2,0000 |
1,6180 |
0,6180 |
||||
|
6 |
0,5176 |
1,4142 |
1,9319 |
1,9319 |
1,4142 |
0,5176 |
|||
|
7 |
0,4450 |
1,2470 |
1,8019 |
2,0000 |
1,8019 |
1,2470 |
0,4450 |
||
|
8 |
0,3902 |
1,1111 |
1,6629 |
1,9616 |
1,9616 |
1,6629 |
1,1111 |
0,3902 |
|
|
9 |
0,3473 |
1,0000 |
1,5321 |
1,8794 |
2,0000 |
1,8794 |
1,5321 |
1,0000 |
0,3473 |
Таблица 8.3.
Значения элементов фильтров Чебышева при Амакс = 1 дБ
Частота среза
Диапазон частот, для которого фильтр не вызывает значительного ослабления, называется полосой пропускания, а диапазон частот, для которых фильтр вызывает существенное ослабление, называется полосой задерживания. Аналоговые фильтры, такие как RC фильтр нижних частот, переходят из полосы пропускания в полосу задерживания всегда постепенно. Это означает, что невозможно идентифицировать одну частоту, на которой фильтр прекращает пропускать сигналы и начинает их блокировать. Однако инженерам нужен способ, чтобы удобно и кратко охарактеризовать амплитудно-частотную характеристику фильтра, и именно здесь в игру вступает понятие частоты среза.
Когда вы посмотрите на график амплитудно-частотной характеристики RC фильтра, вы заметите, что термин «частота среза» не очень точен. Изображение спектра сигнала, «разрезанного» на две половины, одна из которых сохраняется, а другая отбрасывается, неприменимо, поскольку затухание увеличивается постепенно по мере того, как частоты перемещаются от значений ниже частоты среза к значениям выше частоты среза.
Частота среза RC фильтра нижних частот фактически является частотой, на которой амплитуда входного сигнала уменьшается на 3 дБ (это значение было выбрано, поскольку уменьшение амплитуды на 3 дБ соответствует снижению мощности на 50%). Таким образом, частоту среза также называют частотой -3 дБ, и на самом деле это название является более точным и более информативным. Термин полоса пропускания относится к ширине полосы пропускания фильтра, и в случае фильтра нижних частот полоса пропускания равна частоте -3 дБ (как показано на диаграмме ниже).
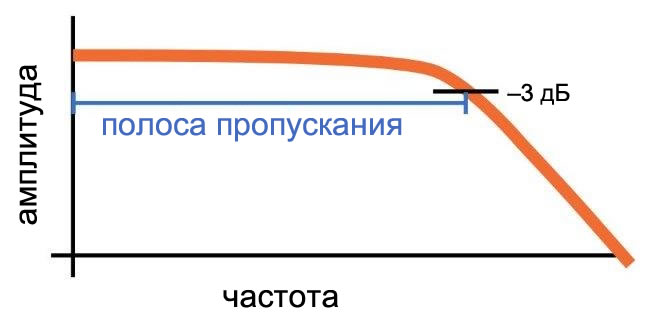
Рисунок 8 – Данная диаграмма показывает общие особенности амплитудно-частотной характеристики RC фильтра нижних частот. Ширина полосы пропускания равна частоте -3 дБ.
Как объяснялось выше, пропускающее низкие частоты поведение RC фильтра обусловлено взаимодействием между частотно-независимым импедансом резистора и частотно-зависимым импедансом конденсатора. Чтобы определить подробности амплитудно-частотной характеристики фильтра, нам нужно математически проанализировать взаимосвязь между сопротивлением (R) и емкостью (C); мы также можем манипулировать этими значениями, чтобы разработать фильтр, который соответствует точным спецификациям. Частота среза (fср) RC фильтра нижних частот рассчитывается следующим образом:
\
Давайте посмотрим на простой пример. Значения конденсаторов являются более сдерживающими, чем значения резисторов, поэтому мы начнем с распространенного значения емкости (например, 10 нФ), а затем воспользуемся формулой для определения необходимого значения сопротивления. Цель состоит в том, чтобы разработать фильтр, который будет сохранять аудиосигнал 5 кГц и подавлять шум 500 кГц. Мы попробуем частоту среза 100 кГц, а позже в этой статье мы более тщательно проанализируем влияние этого фильтра на обе частотные составляющие.
\
Таким образом, резистор 160 Ом в сочетании с конденсатором 10 нФ даст нам фильтр, который дает амплитудно-частотную характеристику, близкую к необходимой.
Построение цифрового фильтра с конечной импульсной характеристикой
Вступление издалека
Недавно передо мной встала достаточно интересная задача, с которой я раньше никогда не сталкивался — борьба с шумом. Мы принимали сигнал с датчиков на аналогово-цифровой преобразователь (АЦП) А так как данная тема для меня была (хотя и сейчас есть кое-где) темным лесом, я пошел мучить вопросами гугл, мне показалось освещена эта тема не очень подробно и доступно, поэтому решил написать статью с примером разработки и готовым исходником.
Ближе к делу
Цифровые фильтры могут быть двух видов – с конечной и с бесконечной импульсной характеристикой (КИХ и БИХ). Для решения моей задачи подходит КИХ-фильтр, поэтому про него и расскажу. Для начала посмотрим как же он работает:
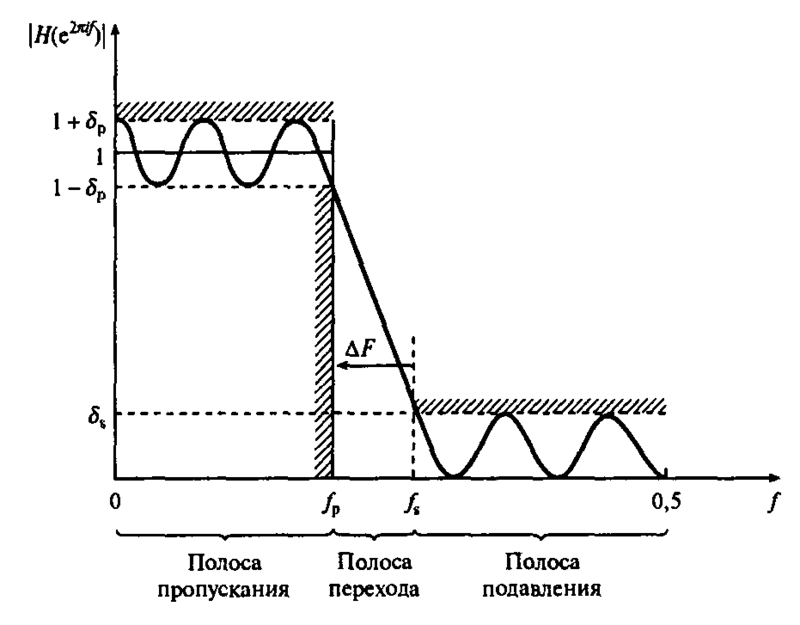
Здесь показан пример фильтра нижних частот, как видно на рисунке, этот фильтр пропускает нижние частоты, а все остальные старается отсечь (подавление), или хотя бы ослабить (переход). Отклонения в полосе пропускания и полосе подавления выбираются в зависимости от принимаемого сигнала, но при использовании различных весовых функций, на них могут накладываться определенные ограничения. Например, если используется весовая функция Хэмминга, то эти отклонения будут равны между собой. Ширина полосы перехода ∆F зависит от длины фильтра и от весовой функции (для функции Блэкмена ∆F=5,5|N).
Работает фильтр довольно просто: фильтр получает значения, с помощью коэффициентов преобразует их и выдаёт выходную последовательность, тогда с формулой самого фильтра всё понятно:
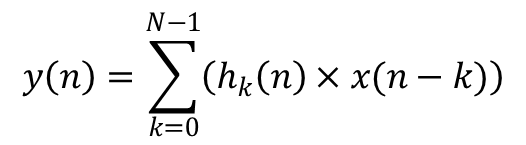
Она реализуется через цикл, но постойте, а где же взять нужные коэффициенты? Вот тут-то как раз и зарыта собака (и не одна).
Параметры фильтра
Естественно для разных фильтров нужны разные коэффициенты, и для этого нужно определиться с параметрами фильтра, это обычно сначала делается теоретически (с умным видом прикидываем какая у нашего сигнала частота, потом частоты, которые надо отсеивать), а потом изучаем АЧХ реальных измерений (и осознаем, как сильно мы ошибались). По этим АЧХ мы определяемся с идеальной частотной характеристикой (какие частоты проходят свободно, какие мы убираем и как сильно), теперь нам нужна идеальная импульсная характеристика её можно посчитать как Фурье-образ от идеальной частотной: где H_D(w) – идеальная характеристика.
Но можно пойти и по более простому пути – есть уже заранее вычисленные идеальные импульсные характеристики, например для фильтра нижних частот формула выглядит следующим образом:
где fc и wc – частота среза.
Итак, осталось уже немного идеал идеалом, а мы имеем дело с практикой, и нам нужна «реальная» импульсная характеристика. Для её расчета нам понадобится весовая функция w(n), их есть несколько разновидностей, в зависимости от требований к фильтру (Хэмминга, Хеннинга, Блэкмена, Кайзера, о них не говорю, ибо статья и так большая), в нашем случае я использую функцию Блэкмена:
где N – длина фильтра, т.е. количество коэффициентов.
Теперь надо перемножить идеальную импульсную характеристику и весовую функцию:
Финишная прямая
Теперь мы готовы рассчитать выходные значения, по формуле фильтра, она самая первая в этой статье, ну вот и всё, в завершение привожу исходный код фильтра: void Filter (const double in[], double out[], int sizeIn) { const int N = 20; //Длина фильтра long double Fd = 2000; //Частота дискретизации входных данных long double Fs = 20; //Частота полосы пропускания long double Fx = 50; //Частота полосы затухания long double H = {0}; //Импульсная характеристика фильтра long double H_id = {0}; //Идеальная импульсная характеристика long double W = {0}; //Весовая функция //Расчет импульсной характеристики фильтра double Fc = (Fs + Fx) / (2 * Fd); for (int i=0;i=0) out+= H*in; } }При подготовке статьи использовались: Основные характеристики и параметры фильтров. analogiu.ru/6/6-5-2.html Айфичер Э. Джервис Б. Цифровая обработка сигналов. Практический подход. 2-е издание
Практическая работа
Плавно переходим от теории к практике. Достались мне винтажные колонки под названием Kompaktbox B 9251. И первое что было сделано — произведено прослушивание.
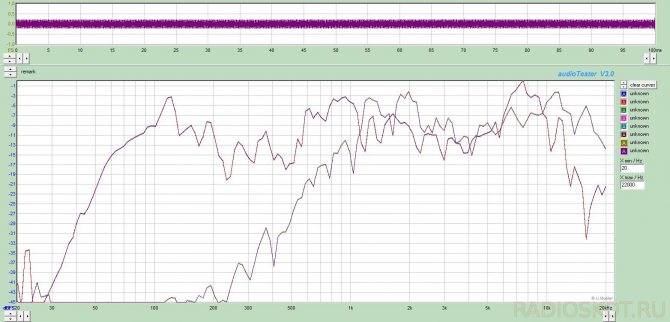
С холодным камнем звук был в среднем не плох, а если говорить конкретно, то местами хороший, а местами как попало. С теплой лампой играть вообще отказались. На основе этих наблюдений был сделан вывод о наличии глубоко зарытого потенциала. Вскрытие показало, что немецкие инженеры решили обойтись одним единственным конденсатором последовательно с ВЧ головкой. Измерение АЧХ дало страшную картину
На рисунке АЧХ одной колонки, кривая с глубокой дыркой на 6 кгц из-за плохого контакта разъема, на нее внимание не обращать. АЧХ отдельно ВЧ и НЧ приведены ниже
RС-фильтры
RС-фильтр высоких частот
Схема RC-фильтра верхних (высоких) частот и его амплитудно-частотная характеристика показаны на рис. 1.
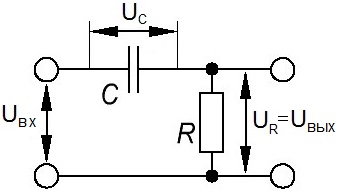
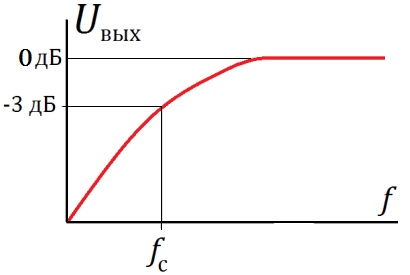
Рис. 1 — Схема и амплитудно-частотная характеристика высокочастотного CR-фильтра.
В этой схеме входное
напряжение прикладывается и к резистору,
и к конденсатору. Выходное же напряжение
снимается с сопротивления. При уменьшении
частоты сигнала возрастает реактивное
сопротивление конденсатора, а
следовательно, и полное сопротивление
цепи. Поскольку входное напряжение
остается постоянным, то ток, протекающий
через цепь уменьшается. Таким образом,
снижается и ток через активное
сопротивление, что приводит к уменьшению
падения напряжения на нем.
Фильтр характеризуется
затуханием, выраженным в децибелах,
которое он обеспечивает на заданной
частоте. RC-фильтры
рассчитываются таким образом, чтобы на выбранной частоте среза коэффициент передачи снижался приблизительно на 3
дБ (т.е. составлял 0,707 входного значения сигнала). Частота среза фильтра по уровню — 3 дБ определяется по формуле:
RС-фильтр низких частот
Фильтр низких частот имеет аналогичную структуру,
только емкость и сопротивление там
меняются местами. Амплитудно-частотную
характеристику такого фильтра можно
представить как зеркальное отображение
АЧХ предыдущего.
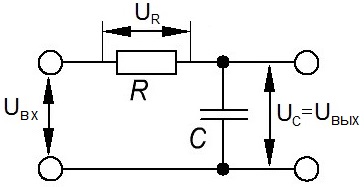
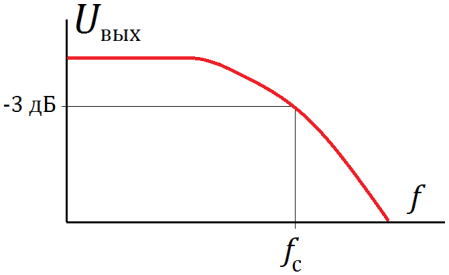
Рис. 2 — Схема и амплитудно-частотная характеристика низкочастотного RC-фильтра.
В этой цепи входное
напряжение также прикладывается и к
резистору, и к конденсатору, но выходное
напряжение снимается с конденсатора.
При увеличении частоты сигнала реактивное
сопротивление конденсатора, а
следовательно, и полное сопротивление
уменьшаются. Однако, поскольку это
полное сопротивление состоит из
реактивного и фиксированного активного
сопротивлений, его значение уменьшается
не так быстро, как реактивное сопротивление.
Следовательно, при увеличении частоты
снижение реактивного сопротивления (относительно полного сопротивления) приводит к уменьшению выходного напряжения. Частота среза этого фильтра по уровню -3 дБ также определяется по формуле предыдущего фильтра.
Рассмотренные
выше фильтры представляют собой RC-цепи,
которые характеризуются тремя параметрами,
а именно: активным, реактивным и полным
сопротивлениями. Обеспечиваемая этими
RC-фильтрами величина затухания зависит от отношения
активного или реактивного сопротивления
к полному сопротивлению.
При расчете любого RC-фильтра можно задать номинал либо резистора, либо конденсатора и вычислить значение другого элемента фильтра на заданной частоте среза. При практических расчетах
обычно задают номинал сопротивления,
поскольку он выбирается на основании
других требований. Например, сопротивление
фильтра является его выходным или
входным полным сопротивлением.
Полосовой RC-фильтр
Соединяя фильтры
верхних и нижних частот, можно создать
полосовой RC-фильтр,
схема и амплитудно-частотная характеристика
которого приведены на рис. 3.
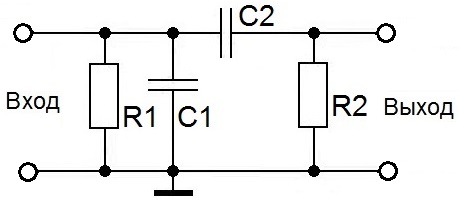
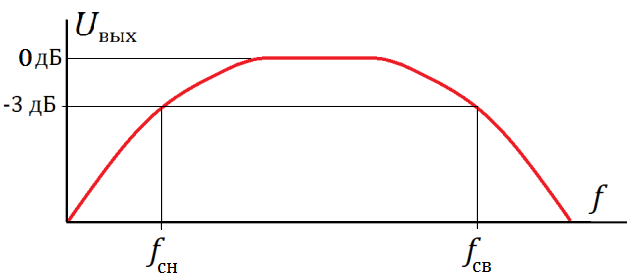
Рис. 3 — Схема и АЧХ полосового RC-фильтра.
На схеме рис. 2. R1 — полное входное сопротивление; R2 —
полное выходное сопротивление, а частоты
низкочастотного и высокочастотного
срезов определяются по формулам:
Следует отметить,
что значение верхней частоты среза
()
должно быть по крайней мере быть в 10 раз
больше нижней частоты среза (),
поскольку только в этом случае
полосно-пропускающий фильтр будет
работать достаточно эффективно.
Многозвенные RC-фильтры
Одиночный RC-фильтр
не может обеспечить достаточного
подавления сигналов вне заданного
диапазона частот, поэтому для формирования
более крутой переходной области довольно
часто используют многозвенные фильтры
(рис. 4, 5). Частота среза многозвенного
фильтра определяется по формуле ВЧ, НЧ
RC-фильтра.
Добавление каждого звена приводит к
увеличению затухания на заданной частоте
среза примерно на 6 дБ.
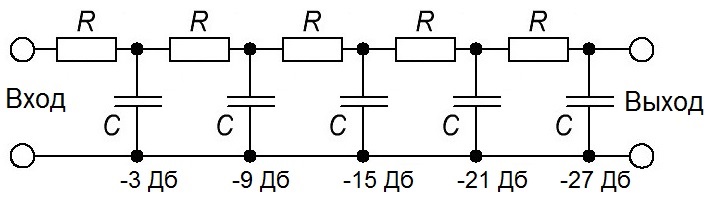
Рис. 4 — Многозвенный высокочастотный фильтр
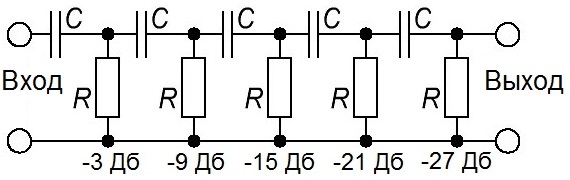
Рис. 5 — Многозвенный низкочастотный фильтр