Программирование&музыка: частотный фильтр баттервота. часть 3 / хабр

Определение частоты среза

Кривая на диаграмме Найквиста, конечно, не имеет типового спада характеристики, который мы хорошо знаем из графиков амплитудно-частотных характеристик, и фактически график Найквиста не дает нам конкретной информации о частоте среза схемы фильтра. Однако изучение взаимосвязи между частотой среза и кривой Найквиста является хорошим способом укрепить понимание концепции частоты среза в целом, а также даст нам некоторое представление об ограничениях подхода Найквиста для визуального изображения частотной характеристики.

Во-первых, нам нужно подумать о том, что на самом деле происходит на частоте среза, с точки зрения как амплитудно-частотной, так и фазо-частотной характеристики.

Частота среза относительно амплитуды

Вы, вероятно, знаете, что другое название для частоты среза – это «частота 3 дБ» (или –3 дБ), и это напоминает нам о том, что фильтр нижних частот первого порядка обеспечивает ослабление на 3 дБ (или, что эквивалентно, усилению –3 дБ), когда входная частота равна ω. Мы не используем децибелы на графике Найквиста, поэтому вместо –3 дБ мы используем соответствующий коэффициент передачи в разах, который равен \(\frac{1}{\sqrt{2}}\)

Когда мы работаем с графиком в полярной системе координат, мы всегда должны помнить о треугольниках; например, амплитуда (модуль) комплексного числа определяется как гипотенуза прямоугольного треугольника, два катета которого являются действительной и мнимой частями; а для вычисления фазы (угла) комплексного числа мы используем тригонометрические функции. Теперь, когда вы думаете с точки зрения треугольников, коэффициент \(\frac{1}{\sqrt{2}}\) дает вам какие-нибудь идеи?

Рисунок 2 – Прямоугольный треугольник. Длина катетов равна 1

Как показано выше, коэффициент \(\sqrt{2}\) вступает в игру всякий раз, когда у прямоугольного треугольника два катета равной длины. Если уменьшить длину катетов до 0,5, длина гипотенузы будет равна \(\sqrt{2} \times 0,5\), что то же самое, что \(\frac{1}{\sqrt{2}}\).

Рисунок 3 – Прямоугольный треугольник. Длина катетов равна 0,5

Итак, что же всё это значит? Рассмотрим следующий график Найквиста:

Рисунок 4 – Это график Найквиста для фильтра нижних частот первого порядка

Обратите внимание, что я не добавил часть графика, которая соответствует отрицательным частотам

Как видите, в самой нижней точке кривой коэффициент усиления фильтра равен \(\frac{1}{\sqrt{2}}\), где абсолютное значение действительной части равно абсолютному значению мнимой части; это и есть местоположение частоты среза на графике Найквиста для фильтра нижних частот первого порядка. То же самое отношение применяется к фильтру верхних частот первого порядка, за исключением того, что в этом случае частота среза находится в самой высокой точке кривой:

Рисунок 5 – Частота среза фильтра верхних частот первого порядка на диаграмме Найквиста

Разница заключается в том, что сдвиг фазы фильтра верхних частот с увеличением частоты изменяется от +90° до 0°, тогда как фаза фильтра нижних частот изменяется от 0° до –90°. Поскольку угол измеряется против часовой стрелки от положительной действительной оси, положительный сдвиг фазы отображается над действительной осью, а отрицательный сдвиг фазы отображается ниже действительной оси.

Также обратите внимание, что на этих двух графиках есть стрелки, указывающие в противоположных направлениях: на графике фильтра нижних частот стрелка указывает на начало координат, поскольку с увеличением частоты коэффициент усиления уменьшается; на графике фильтра верхних частот она указывает в сторону от начала координат, поскольку с увеличением частоты коэффициент усиления увеличивается

Частота среза относительно сдвига фазы

Мы также можем найти частоту среза на графике Найквиста, если вспомнить, что сдвиг фазы на 90°, создаваемый фильтром первого порядка, центрирован относительно частоты среза. Другими словами, фазовый сдвиг при ω составляет +45° или –45°. Вектор, нарисованный в комплексной плоскости, будет иметь угол +45° или –45°, если его действительная и мнимая части имеют одинаковые абсолютные значения, и это приводит нас к тем же геометрическим соотношениям, которые мы обнаружили при рассмотрении частоты среза с точки зрения амплитуды отклика.

Рисунок 6 – Частота среза фильтра нижних частот первого порядка на диаграмме НайквистаРисунок 7 – Частота среза фильтра верхних частот первого порядка на диаграмме Найквиста

Линейные фильтры с непрерывным временем

Линейная схема с непрерывным временем, пожалуй, наиболее распространенное значение для фильтра в мире обработки сигналов, и просто «фильтр» часто считается синонимом. Эти схемы обычно предназначены для удаления определенных частот и пропуска других. Цепи, которые выполняют эту функцию, обычно имеют линейный отклик или, по крайней мере, приблизительно таковы . Любая нелинейность потенциально может привести к тому, что выходной сигнал будет содержать частотные компоненты, отсутствующие во входном сигнале.

Современная методология проектирования линейных фильтров с непрерывным временем называется сетевым синтезом . Вот некоторые важные семейства фильтров, разработанные таким образом:

Фильтр Чебышева , имеет наилучшее приближение к идеальному отклику любого фильтра для указанного порядка и пульсации.
Фильтр Баттерворта , имеет максимально ровную АЧХ.
Фильтр Бесселя имеет максимально плоскую фазовую задержку .
Эллиптический фильтр имеет самое крутое отсечение из всех фильтров для указанного порядка и пульсации.

Разница между этими семействами фильтров состоит в том, что все они используют разные полиномиальные функции для приближения к идеальному отклику фильтра . Это приводит к тому, что каждый из них имеет различную передаточную функцию .

Еще одна старая, менее используемая методология — это метод параметров изображения . Фильтры, разработанные по этой методике, архаично называются «волновыми фильтрами». Некоторые важные фильтры, разработанные этим методом:

Постоянный k-фильтр , оригинальная и простейшая форма волнового фильтра.
Фильтр на основе m , модификация постоянной k с улучшенной крутизной среза и согласованием импеданса .

Терминология

Некоторые термины, используемые для описания и классификации линейных фильтров:

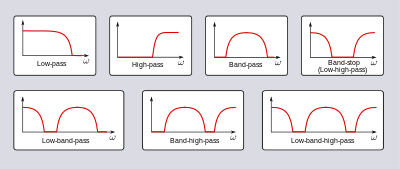
Амплитудно-частотную характеристику можно разделить на несколько различных полос частот, описывающих, какие полосы частот пропускает фильтр ( полоса пропускания ), а какие отклоняет ( полоса задерживания ):
- Фильтр низких частот — низкие частоты пропускаются, высокие — приглушаются.
- Фильтр высоких частот — высокие частоты пропускаются, низкие частоты приглушаются.
- Полосовой фильтр —
пропускаются только частоты в полосе частот.
Полосовой фильтр или режекторный фильтр — ослабляются только частоты в полосе частот.
Режекторный фильтр — отклоняет только одну конкретную частоту — крайний полосовой фильтр.
Гребенчатый фильтр — имеет несколько равномерно расположенных узких полос пропускания, придающих полосе вид гребенки.
Пропускной фильтр — пропускаются все частоты, но изменяется фаза выхода.

Частота среза — это частота, за которой фильтр не будет пропускать сигналы. Обычно он измеряется при определенном затухании, например, 3 дБ.

Спад — это скорость, с которой затухание увеличивается сверх частоты среза.

Полоса перехода , (обычно узкая) полоса частот между полосой пропускания и полосой задерживания.

— это изменение вносимых потерь фильтра в полосе пропускания.
Порядок фильтра — это степень аппроксимирующего полинома, а в пассивных фильтрах соответствует количеству элементов, необходимых для его построения. Порядок увеличения увеличивает спад и приближает фильтр к идеальному отклику.

Одно из важных применений фильтров — это телекоммуникации . Многие телекоммуникационные системы используют мультиплексирование с частотным разделением , при котором разработчики системы делят широкую полосу частот на множество более узких полос частот, называемых «временными интервалами» или «каналами», и каждому потоку информации выделяется один из этих каналов. Люди, которые проектируют фильтры на каждом передатчике и каждом приемнике, пытаются сбалансировать прохождение полезного сигнала как можно точнее, сохраняя как можно меньше помех от других взаимодействующих передатчиков и источников шума за пределами системы при разумных затратах.

Для многоуровневых и многофазных систем цифровой модуляции требуются фильтры с плоской фазовой задержкой — линейной фазой в полосе пропускания — для сохранения целостности импульса во временной области, что дает меньше межсимвольных помех, чем другие типы фильтров.

С другой стороны, аналоговые аудиосистемы , использующие аналоговую передачу, могут допускать гораздо большие колебания фазовой задержки , и поэтому разработчики таких систем часто сознательно жертвуют линейной фазой, чтобы получить фильтры, которые лучше в других отношениях — лучшее подавление полосы задерживания, меньшая амплитуда полосы пропускания. рябь, более низкая стоимость и т. д.

1.2 ЭЛЕМЕНТЫ АКТИВНЫХ ФИЛЬТРОВ

Как только получена
подходящая передаточная функция, разрабатывают схему фильтра, реализующую
данную передаточную функцию. При этом разработка выливается в проектирование
активных и пассивных фильтров.

Таким образом, для
применения фильтров в диапазоне низких частот из схем желательно исключить
катушки индуктивности. Это достигается разработкой активных фильтров на
основе резисторов, конденсаторов и одного или нескольких активных приборов,
таких как транзисторы, зависимые источники и т. д.

Активные
фильтры построены из сопротивлений, конденсаторов и усилителей (обычно
операционных) и предназначены для того, чтобы из всех подаваемых на их вход
сигналов пропускать на выход сигналы лишь некоторых заранее заданных частот.
Эти обладающие частотной избирательностью схемы используются для усиления или
ослабления определенных частот в звуковой аппаратуре, в генераторах
электромузыкальных инструментов, в сейсмических приборах, в линиях связи, а
также в исследовательской практике для изучения частотного состава самых
разнообразных сигналов, таких, например, как биотоки мозга или механические
вибрации. Активные фильтры находят применение почти в любой области электроники
и потому заслуживают нашего внимания .

Одним из наиболее часто
применяемых активных приборов, который в основном и будет использоваться,
является интегральная схема (ИС) операционного усилителя или ОУ условное
изображение которого приведено на рис.3.

Рис. 3. Операционный
усилитель.

Операционный усилитель
представляет собой многовходовый прибор, но для простоты показаны только три
его вывода: инвертирующий входной (1), неинвертирующий входной (2) и выходной
(3). В идеальном случае ОУ обладает бесконечным входным и нулевым выходным
сопротивлениями и бесконечным коэффициентом усиления. Вследствие этого можно,
при исследованиях рассматривать только напряжение между входными выводами, а
также считать, что ток во входных выводах равен нулю. Реальные ОУ по своим
характеристикам приближаются к идеальным наиболее близко только для
ограниченного диапазона частот, который зависит от типа ОУ.

Непоказанные на рис. 3
выводы — это обычно выводы подключения источника питания; выводы подключения
цепей коррекции, требуемой для ОУ, например типа 709; и выводы балансировки
нуля, необходимые для ОУ, типа 741. Эти дополнительные выводы используются в
соответствии с рекомендациями, предоставляемыми фирмой-изготовителем. В
основном ОУ с внешними цепями коррекции имеют лучшие результаты на более
высоких частотах по сравнению с ОУ с внутренней коррекцией, которые не имеют
выводов для подключения цепей коррекции.

При реализации активного
фильтра разработчик должен применять те же типы ОУ, которые отвечают
предъявленным требованиям по коэффициентам усиления и частотным диапазонам.
Например, коэффициент усиления ОУ с разомкнутой обратной связью должен по
крайней мере в 50 раз превышать коэффициент усиления фильтра.

В некритических
конструкциях фильтров наиболее часто используются дешевые угольные
композиционные резисторы. Для фильтров четвертого и более низкого порядка
достаточно применять угольные композиционные резисторы с 5%-ными допусками, в
частности, если предполагается использовать фильтр при комнатной температуре.
Для фильтров с высокими рабочими характеристиками необходимо применять
высококачественные типы резисторов. Чем выше порядок, тем меньше должны быть
допуски. Фильтры с порядком выше четвертого необходимо реализовывать на
резисторах с 2%-ным
или меньшими допусками.

Что касается
конденсаторов, то наиболее подходящим типом является майларовый конденсатор,
который можно успешно применять в большинстве конструкций фильтров.
Конденсаторы на основе полистирола и тефлона лучше, но применяются в высококачественных
фильтрах. Обычные экономичные дисковые керамические конденсаторы должны
использоваться исключительно в наименее критических условиях.

Математическое описание

Полосовой фильтр может быть представлен как комбинация фильтров нижних и верхних частот, если полоса пропускания достаточно велика, чтобы два фильтра не слишком сильно взаимодействовали. Более общий подход заключается в разработке прототипа фильтра нижних частот, который затем может быть преобразован в ограничитель полосы пропускания . Показанный простой режекторный фильтр можно непосредственно проанализировать. Передаточная функция:

ЧАС ( s ) знак равно s 2 + ω z 2 s 2 + ω п Q s + ω п 2 {\ displaystyle H (s) = {\ frac {s ^ {2} + \ omega _ {z} ^ {2}} {s ^ {2} + {\ frac {\ omega _ {p}} {Q} } s + \ omega _ {p} ^ {2}}}}

Здесь нулевая круговая частота и полюсная круговая частота. Нулевая частота является частотой среза и устанавливает тип режекторного фильтра: стандартный режекторный фильтр, режекторный фильтр нижних частот ( ) и режекторный фильтр верхних частот ( ). обозначает добротность.
ω z {\ displaystyle \ omega _ {z}} ω п {\ displaystyle \ omega _ {p}} ω п {\ displaystyle \ omega _ {p}} ω z знак равно ω п {\ displaystyle \ omega _ {z} = \ omega _ {p}} ω z > ω п {\ displaystyle \ omega _ {z}> \ omega _ {p}} ω z < ω п {\ displaystyle \ omega _ {z} <\ omega _ {p}} Q {\ displaystyle Q}

Для стандартного режекторного фильтра формулировку можно переписать как

ЧАС ( s ) знак равно s 2 + ω 2 s 2 + ω c s + ω 2 , {\ displaystyle H (s) = {\ frac {s ^ {2} + \ omega _ {0} ^ {2}} {s ^ {2} + \ omega _ {c} s + \ omega _ {0} ^ {2}}},}

где — центральная частота отклонения, а — ширина полосы отклонения.
ω {\ displaystyle \ omega _ {0}} ω c {\ displaystyle \ omega _ {c}}

Сложные фильтры

Что будет, если соединить два фильтра первого порядка друг за другом? Как ни странно, получится фильтр второго порядка.

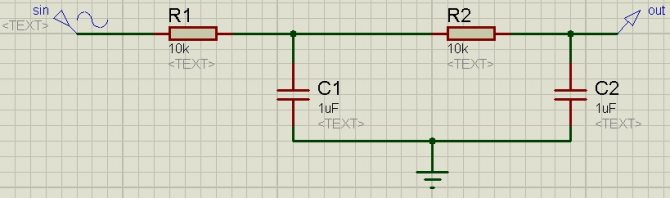
Его АЧХ будет более крутой, а именно 12 дБ/октаву, что характерно для фильтров второго порядка. Догадайтесь, какой наклон будет у фильтра третьего порядка

В приведенных схемах мы строили АЧХ фильтра без внутреннего сопротивления генератора а также без нагрузки. То есть в данном случае сопротивление на выходе фильтра равняется бесконечности. Значит, желательно делать так, чтобы каждый последующий каскад имел значительно бОльшее входное сопротивление, чем предыдущий. В настоящее время каскадирование звеньев уже кануло в лету и сейчас используют активные фильтры, которые построены на ОУ.

Полосовые фильтры

В прошлой статье мы с вами рассматривали один из примеров полосового фильтра

Вот так выглядит АЧХ этого фильтра.

Особенность таких фильтров такова, что они имеют две частоты среза. Определяются они также на уровне в -3дБ или на уровне в 0,707 от максимального значения коэффициента передачи, а еще точнее Ku max/√2.

Полосовые резонансные фильтры

Если нам надо выделить какую-то узкую полосу частот, для этого применяются LC-резонанcные фильтры. Еще их часто называют избирательными. Давайте рассмотрим одного из их представителя.

LC-контур в сочетании с резистором R образует делитель напряжения. Катушка и конденсатор в паре создают параллельный колебательный контур, который на частоте резонанса будет иметь очень высокий импеданс, в народе – обрыв цепи. В результате, на выходе цепи при резонансе будет значение входного напряжения, при условии если мы к выходу такого фильтра не цепляем никакой нагрузки.

АЧХ данного фильтра будет выглядеть примерно вот так:

В реальной же цепи пик характеристики АЧХ будет сглажен за счет потерь в катушке и конденсаторе, так как катушка и конденсатор обладают паразитными параметрами.

Если взять по оси Y значение коэффициента передачи, то график АЧХ будет выглядеть следующим образом:

Постройте прямую на уровне в 0,707 и оцените полосу пропускания такого фильтра. Как вы можете заметить, она будет очень узкой. Коэффициент добротности Q позволяет оценить характеристику контура. Чем большее добротность, тем острее характеристика.

Как же определить добротность из графика? Для этого надо найти резонансную частоту по формуле:

где

f0— это резонансная частота контура, Гц

L — индуктивность катушки, Гн

С — емкость конденсатора, Ф

Подставляем L=1mH и С=1uF и получаем для нашего контура резонансную частоту в 5033 Гц.

Теперь надо определить полосу пропускания нашего фильтра. Делается это как обычно на уровне в -3 дБ, если вертикальная шкала в децибелах, либо на уровне в 0,707, если шкала линейная.

Давайте увеличим верхушку нашей АЧХ и найдем две частоты среза.

f1 = 4839 Гц

f2 = 5233 Гц

Следовательно, полоса пропускания Δf=f2 – f1 = 5233-4839=394 Гц

Ну и осталось найти добротность:

Q=5033/394=12,77

Режекторные фильтры

Другой разновидностью LC схем является последовательная LC-схема.

Ее АЧХ будет выглядеть примерно вот так:

Как можно увидеть, такая схема на резонансной частоте и вблизи нее как бы вырезает небольшой диапазон частот. Здесь вступает в силу резонанс последовательного колебательного контура. Как вы помните, на резонансной частоте сопротивление контура будет равняться его активному сопротивлению. Активное сопротивление контура составляют паразитные параметры катушки и конденсатора, поэтому падение напряжения на самом контуре будет равняться падению напряжения на паразитном сопротивлении, которое очень мало. Такой фильтр называют узкополосным режекторным фильтром.

На практике звенья таких фильтров каскадируют, чтобы получить различные фильтры с требуемой полосой пропускания. Но есть один минус у фильтров, в которых имеется катушка индуктивности. Катушки дорогие, громоздкие, имеют много паразитных параметров. Они чувствительны к фону, который магнитным путем наводится от расположенных поблизости силовых трансформаторов.

Конечно, этот недостаток можно устранить, поместив катушку индуктивности в экран из мю-металла, но от этого она станет только дороже. Проектировщики всячески пытаются избежать катушек индуктивности, если это возможно. Но, благодаря прогрессу, в настоящее время катушки не используются в активных фильтрах, построенных на ОУ.

Видео на тему “Как работает электрический фильтр”, рекомендую к просмотру:

Что такое фильтр?

Фильтр – это схема, которая удаляет или «отфильтровывает» определенный диапазон частотных компонентов. Другими словами, он разделяет спектр сигнала на частотные составляющие, которые будут передаваться дальше, и частотные составляющие, которые будут блокироваться.

Если у вас нет большого опыта анализа частотной области, вы можете быть не уверены в том, что представляют собой эти частотные компоненты и как они сосуществуют в сигнале, который не может иметь несколько значений напряжения одновременно. Давайте рассмотрим краткий пример, который поможет прояснить эту концепцию.

Давайте представим, что у нас есть аудиосигнал, который состоит из идеальной синусоидальной волны 5 кГц. Мы знаем, как выглядит синусоида во временной области, а в частотной области мы не увидим ничего, кроме частотного «всплеска» на 5 кГц. Теперь предположим, что мы включили генератор на 500 кГц, который вносит в аудиосигнал высокочастотный шум.

Сигнал, видимый на осциллографе, будет по-прежнему представлять собой только одну последовательность напряжений с одним значением на момент времени, но он будет выглядеть по-другому, поскольку его изменения во временной области теперь должны отражать как синусоидальную волну 5 кГц, так и высокочастотные колебания шума.

Однако в частотной области синусоида и шум являются отдельными частотными компонентами, которые присутствуют одновременно в этом одном сигнале. Синусоидальная волна и шум занимают разные участки представления сигнала в частотной области (как показано на диаграмме ниже), и это означает, что мы можем отфильтровать шум, направив сигнал через схему, которая пропускает низкие частоты и блокирует высокие частоты.

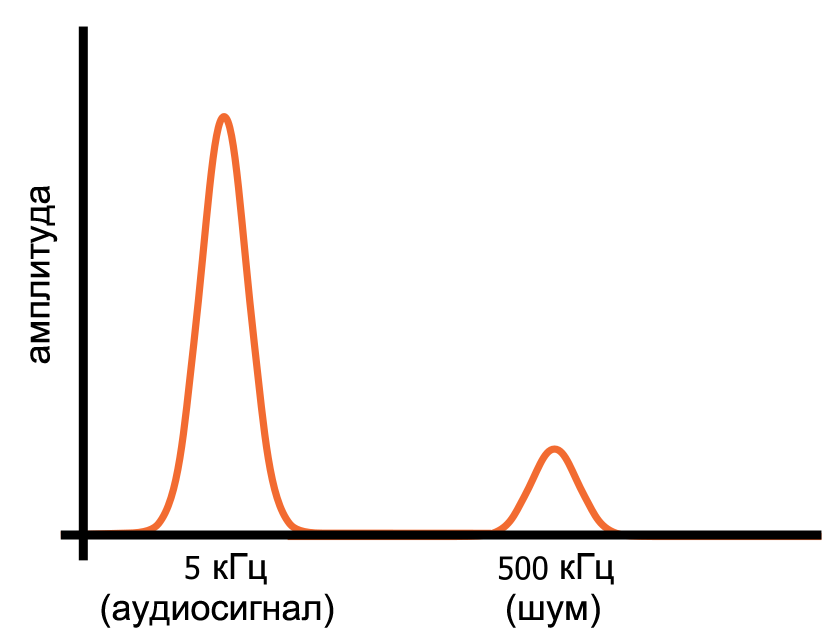Рисунок 3 – Представление аудиосигнала и высокочастотного шума в частотной области

5.1 РАСЧЕТ ФНЧ ЧЕТВЕРТОГО ПОРЯДКА

Фильтр
получен путем каскадного включения двух ФНЧ второго порядка.

Расчет
ведется в соответствии с п. 2.4. Коэффициенты звена второго порядка фильтра
Баттерворта берутся из приложения A . Для звена второго порядка В=1,1 и С=1,1. По условию курсовой работы
К=1 и f_c=18000 Гц.

·
Значение емкости
С₁ выбирается близким к значению 10/f_c мкФ.

10/f_c
мкФ=10/18000 мкФ=0,55 нФ.

Выберем
значение С₁=0,6нФ.

С₂
выбирается из условия

Получаем
условие С₂£0,165 нФ. Выбираем С₂=0,16 нФ.

R₁ находим по формуле

R₁=21,4
кОм.

R₂ находим по формуле

R₂=34,6
кОм.

Значения
элементов C₃, C₄, R₃ и R₄ выбираем следующими:

C₃=C₁=0,6нФ, C₄=C₂=0,16 нФ, R₃=R₁=21,4 кОм, R₄=R₂=34,6 кОм.

Ширина — полоса — пропускание — фильтр

Ширина полосы пропускания фильтра определяется параметрами волновода. При широкополосном согласовании возбуждающего и воспринимающего устройств она соответствует диапазону существования комплексных волн.

Ширина полосы пропускания фильтров шумомера или частотного анализатора должна быть равной одной октаве. Допускается применение приборов с шириной полосы пропускания, равной V октавы.

Ширину полосы пропускания фильтра обычно выбирают равной ширине полосы пропускания входного фильтра приемника ВЧ защиты или автоматики.

На ширину полосы пропускания фильтра оказывает большое влияние эквивалентная индуктивность резонатора. Поэтому для получения более широкой полосы следует выбирать срез с малой величиной коэффициента индуктивности, причем при продольных колебаниях толщина пластины резонатора должна быть возможно меньше.

Обычно считают разрешение анализатора удовлетворительным, если ширина полосы пропускания фильтра меньше четверти ширины самого узкого пика спектральной плотности мощности.

Сиелетная схема каяала ТТ с ЧМ 50.

Другие факторы, оказывающие влияние на выбор ширины полосы пропускания фильтра и на выбор отклонения ( девиации) частоты, рассмотрены ниже.

Продолжительность фронта импульса — величина, обратная удвоенной ширине полосы пропускания фильтра.

Схема гетеродина.

Минимально допустимое изменение частоты при манипуляции определяется шириной полос пропускания фильтров, разделяющих колебания положительных и отрицательных посылок в приемнике. Эти полосы пропускания в свою очередь определяются требованиями неискаженного воспроизведения телеграфных сигналов и необходимостью обеспечить устойчивый прием при уходе частот передатчика и гетеродина приемника в процессе эксплуатации. Поэтому применение частотной манипуляции требует обеспечения высокой устойчивости частоты передатчика и гетеродина приемника. В первом гетеродине приемника телеграфных сигналов с частотной манипуляцией применяется кварцевая стабилизация. На рис. 582 показана схема гетеродина с кварцевой стабилизацией, обеспечивающая возможность ручной подстройки частоты в небольших пределах для компенсации уходов частоты передатчика и гетеродина приемника в процессе эксплуатации.

Отклонение резистора и конденсатора от номиналов влияет н r ширину полосы пропускания фильтра так же, как и ненулевой иг педанс источника. Резисторы с допусками 5 или 1 % обходятся дешево, но прецизионные конденсаторы довольно дороги. Однако, поскольку требования к фильтрам в АСУ ТП, как правило, невысоки, влияние этого допуска редко играет заметную роль.

Из (8.87) следует, что время нарастания тн обратно пропорционально ширине полосы пропускания фильтра. Этот вывод вполне очевиден, так как чем шире полоса пропускания системы, тем больше частотных составляющих она пропускает.

Для достаточно узкополосных фильтров среднеквадратичная ошибка оценки спектральной плотности уменьшается при увеличении ширины полосы пропускания фильтра анализатора. Однако не следует забывать, что относительный вклад ошибки смещения в среднеквадратичную ошибку е увеличивается при расширении полосы пропускания, а разрешающая способность анализа снижается. Имеет смысл считать хорошо разрешенными те спектральные составляющие, для которых ошибка смещения мала.

Ширина диапазона частот, в котором производят измерение уровня помех, определяется шириной полосы пропускания фильтра присоединения и полосы заграждения ВЧ заградителя. Точки измерений следует выбирать таким образом, чтобы на частотах измерения отсутствовали сосредоточенные помехи. Помехи от короны создают в наушниках характерный шум, похожий на шум идущего дождя. При измерении уровня помех ( как и вообще при измерениях малых уровней избирательным указателем уровня) следует помнить, что измерение с помощью ИИУ может дать значительную погрешность, если на вход ИИУ дополнительно подается сигнал, превышающий на 30 — 40 дБ измеряемый сигнал. Погрешность обусловливается перегрузкой входного усилительного каскада большим сигналом.

Программирование&музыка: частотный фильтр баттервота. часть 3