При нагреве сопротивление увеличивается или уменьшается. § 48. зависимость сопротивления от температуры

Историческая справка

Медь является металлом, известным человеку с глубокой древности. Объясняется раннее знакомство людей с эти материалом прежде всего его широкой распространенностью в природе в виде самородков. Многие ученые считают, что именно медь была первым металлом, восстановленным человеком из кислородных соединений. Когда-то горные породы просто нагревали на костре и резко остужали, в результате чего они растрескивались. Позднее восстановление меди начали производить на кострах с добавлением угля и поддувом мехами. Совершенствование этого способа в конечном итоге привело к созданию шахтной печи. Еще позже этот металл начали получать методом окислительной плавки руд.

Зависимость сопротивления платинового термосопротивления от температуры

Для промышленных платиновых термометров сопротивления используется уравнение Каллендара-Ван Дьюзена (en), с известными коэффициентами, которые установлены экспериментально и нормированы в стандарте DIN EN 60751-2009 (ГОСТ 6651-2009):

RT=R1+AT+BT2+CT3(T−100)(−200∘CT∘C),{\displaystyle R_{T}=R_{0}\left\;(-200\;{}^{\circ }\mathrm {C}

RT=R1+AT+BT2(∘C≤T850∘C),{\displaystyle R_{T}=R_{0}\left\;(0\;{}^{\circ }\mathrm {C} \leq T

здесь RT{\displaystyle R_{T}} — сопротивление при температуре T{\displaystyle T} °C,

R{\displaystyle R_{0}} сопротивление при 0 °C,

A,B,C{\displaystyle A,B,C} — коэффициенты — константы, нормированные стандартом:

A=3.9083×10−3∘C−1{\displaystyle A=3.9083\times 10^{-3}\;{}^{\circ }\mathrm {C} ^{-1}}

B=−5.775×10−7∘C−2{\displaystyle B=-5.775\times 10^{-7}\;{}^{\circ }\mathrm {C} ^{-2}}

C=−4.183×10−12∘C−4.{\displaystyle C=-4.183\times 10^{-12}\;{}^{\circ }\mathrm {C} ^{-4}.}

Поскольку коэффициенты B{\displaystyle B} и C{\displaystyle C} относительно малы, сопротивление растёт практически линейно при увеличении температуры.

Для платиновых термометров повышенной точности и эталонных термометров выполняется индивидуальная градуировка в ряде температурных реперных точек и определяются индивидуальные коэффициенты вышеприведенной зависимости.

Виды и свойства полупроводников

Все полупроводники можно разделить на несколько основных видов. Среди них лидируют чистые или собственные материалы, в которых отсутствуют какие-либо примеси.

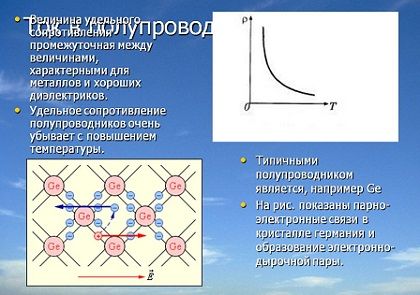
Для них характерна кристаллическая структура, где атомы расположены в периодическом порядке в ее узлах. Здесь существует устойчивая взаимная связь каждого атома с четырьмя атомами, расположенными рядом. Это дает возможность образовывать постоянные электронные оболочки, в состав которых входит восемь электронов. При температуре, равной абсолютному нулю, такой полупроводник становится диэлектриком, поскольку все электроны соединены ковалентными связями. Когда температура повышается или происходит какое-либо облучение, электроны могут выйти из ковалентных связей и превратиться в свободных носителей зарядов. Свободные места при перемещении постепенно занимаются другими электронами, поэтому электрический ток протекает только в одном направлении.

В электронных полупроводниках, кроме четырех атомов, составляющих основу кристаллической решетки, имеются так называемые доноры. Они представляют собой примеси в виде пятивалентных атомов. Электрон, содержащийся в таком атоме, не может нормально вступить в ковалентную связь и поэтому отделяется от донора. Таким образом, он превращается в свободный носитель заряда. В свою очередь донор становится положительным ионом, это может произойти даже при комнатной температуре.

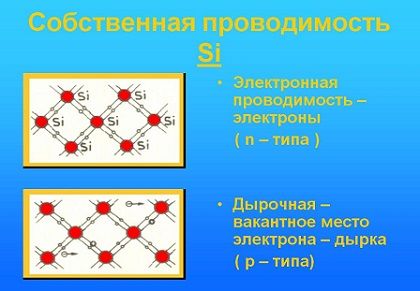
В дырочных полупроводниках имеется кристаллическая решетка с содержанием трехвалентных примесных атомов, называемых акцепторами. В такой решетке остается незаполненной одна ковалентная связь. Она может быть заполнена электроном, оторвавшимся от соседней связи. Происходит превращение примесного атома в отрицательный ион, а на месте ушедшего электрона появляется дырка.То есть, в этом случае также начинается одностороннее движение электрического тока.

Таблица удельных сопротивлений проводников

Материал проводника

Удельное сопротивление ρ в

Серебро Медь Золото Латунь Алюминий Натрий Иридий Вольфрам Цинк Молибден Никель Бронза Железо Сталь Олово Свинец Никелин (сплав меди, никеля и цинка) Манганин (сплав меди, никеля и марганца) Константан (сплав меди, никеля и алюминия) Титан Ртуть Нихром (сплав никеля, хрома, железа и марганца) Фехраль Висмут Хромаль

0,015 0,0175 0,023 0,025… 0,108 0,028 0,047 0,0474 0,05 0,054 0,059 0,087 0,095… 0,1 0,1 0,103… 0,137 0,12 0,22 0,42 0,43… 0,51 0,5 0,6 0,94 1,05… 1,4 1,15… 1,35 1,2 1,3… 1,5

Из таблицы видно, что железная проволока длиной 1 м и сечением 1 мм2 обладает сопротивлением 0,13 Ом. Чтобы получить 1 Ом сопротивления нужно взять 7,7 м такой проволоки. Наименьшим удельным сопротивлением обладает серебро. 1 Ом сопротивления можно получить, если взять 62,5 м серебряной проволоки сечением 1 мм2. Серебро — лучший проводник, но стоимость серебра исключает возможность его массового применения. После серебра в таблице идет медь: 1 м медной проволоки сечением 1 мм2 обладает сопротивлением 0,0175 Ом. Чтобы получить сопротивление в 1 Ом, нужно взять 57 м такой проволоки.

Химически чистая, полученная путем рафинирования, медь нашла себе повсеместное применение в электротехнике для изготовления проводов, кабелей, обмоток электрических машин и аппаратов. Широко применяют также в качестве проводников алюминий и железо.

Сопротивление проводника можно определить по формуле:

где r — сопротивление проводника в омах; ρ — удельное сопротивление проводника; l — длина проводника в м; S — сечение проводника в мм2.

Пример 1. Определить сопротивление 200 м железной проволоки сечением 5 мм2.

Пример 2. Вычислить сопротивление 2 км алюминиевой проволоки сечением 2,5 мм2.

Из формулы сопротивления легко можно определить длину, удельное сопротивление и сечение проводника.

Пример 3. Для радиоприемника необходимо намотать сопротивление в 30 Ом из никелиновой проволоки сечением 0,21 мм2. Определить необходимую длину проволоки.

Пример 4. Определить сечение 20 м нихромовой проволоки, если сопротивление ее равно 25 Ом.

Пример 5. Проволока сечением 0,5 мм2 и длиной 40 м имеет сопротивление 16 Ом. Определить материал проволоки.

Материал проводника характеризует его удельное сопротивление.

По таблице удельных сопротивлений находим, что таким сопротивлением обладает свинец.

Выше было указано, что сопротивление проводников зависит от температуры. Проделаем следующий опыт. Намотаем в виде спирали несколько метров тонкой металлической проволоки и включим эту спираль в цепь аккумулятора. Для измерения тока в цепь включаем амперметр. При нагревании спирали в пламени горелки можно заметить, что показания амперметра будут уменьшаться. Это показывает, что с нагревом сопротивление металлической проволоки увеличивается.

У некоторых металлов при нагревании на 100° сопротивление увеличивается на 40 — 50 %. Имеются сплавы, которые незначительно меняют свое сопротивление с нагревом. Некоторые специальные сплавы практически не меняют сопротивления при изменении температуры. Сопротивление металлических проводников при повышении температуры увеличивается, сопротивление электролитов (жидких проводников), угля и некоторых твердых веществ, наоборот, уменьшается.

Способность металлов менять свое сопротивление с изменением температуры используется для устройства термометров сопротивления. Такой термометр представляет собой платиновую проволоку, намотанную на слюдяной каркас. Помещая термометр, например, в печь и измеряя сопротивление платиновой проволоки до и после нагрева, можно определить температуру в печи.

температурный коэффициент сопротивления

— это изменение сопротивления проводника при его нагревании, приходящееся на 1 Ом первоначального сопротивления и на 1° температуры, обозначается буквой α.

Если при температуре t0 сопротивление проводника равно r0, а при температуре t равно rt, то температурный коэффициент сопротивления

Примечание. Расчет по этой формуле можно производить лишь в определенном интервале температур (примерно до 200°C).

Приводим значения температурного коэффициента сопротивления α для некоторых металлов (таблица 2).

Сфера использования

Высокая тепло- и электропроводность меди определяет ее широкое применение в самых разных отраслях промышленности. Конечно же, чаще всего этот металл используется в электротехнике. Однако это далеко не единственная сфера его применения. Помимо всего прочего, медь может использоваться:

в ювелирном деле;
в архитектуре;
при сборке водопроводных и отопительных систем;
в газопроводах.

Для изготовления разного рода ювелирных изделий используется в основном сплав меди с золотом. Это позволяет увеличить стойкость украшений к деформациям и истиранию. В архитектуре медь может использоваться при облицовке кровель и фасадов. Основным преимуществом такой отделки является долговечность. К примеру, листами именно этого металла обшита крыша широко известной архитектурной достопримечательности — католического собора в немецком городе Хильдесхайме. Медная кровля этого здания надежно защищает его внутреннее пространство вот уже почти 700 лет.

Сопротивление провода

Величина сопротивления провода зависит от трех параметров: удельного сопротивления металла, длины и диаметра самого провода. Формула для расчета сопротивления провода:

где: R — сопротивление провода (Ом) ρ — удельное сопротивление металла (Ом.m) L — длина провода (м) А — площадь поперечного сечения провода (м2)

В качестве примера рассмотрим проволочный резистор из нихрома с удельным сопротивлением 1.10×10-6 Ом.м. Проволока имеет длину 1500 мм и диаметр 0,5 мм. На основе этих трех параметров рассчитаем сопротивление провода из нихрома:

R=1,1*10-6*(1,5/0,000000196) = 8,4 Ом

Нихром и константан часто используют в качестве материала для сопротивлений. Ниже в таблице вы можете посмотреть удельное сопротивление некоторых наиболее часто используемых металлов.

Терморезисторы

Терморезистор — полупроводниковый резистор, электрическое сопротивление которого зависит от температуры.
Для терморезисторов характерны большой температурный коэффициент сопротивления, простота устройства, способность работать в различных климатических условиях при значительных механических нагрузках, стабильность характеристик во времени. Они могут иметь весьма малые размеры, что существенно для измерений температуры малых объектов и снижения инерционности измерения. Обычно терморезисторы имеют отрицательный температурный коэффициент сопротивления, в отличие от большинства металлов и металлических сплавов.

Удельное электрическое сопротивление

Сопротивление в омах проводника длиной 1 м, сечением 1 мм² называется удельным сопротивлением

и обозначается греческой буквойρ (ро).

В таблице 1 даны удельные сопротивления некоторых проводников.

Таблица 1

Удельные сопротивления различных проводников

Из таблицы видно, что железная проволока длиной 1 м и сечением 1 мм² обладает сопротивлением 0,13 Ом. Чтобы получить 1 Ом сопротивления нужно взять 7,7 м такой проволоки. Наименьшим удельным сопротивлением обладает серебро. 1 Ом сопротивления можно получить, если взять 62,5 м серебряной проволоки сечением 1 мм². Серебро – лучший проводник, но стоимость серебра исключает возможность его массового применения. После серебра в таблице идет медь: 1 м медной проволоки сечением 1 мм² обладает сопротивлением 0,0175 Ом. Чтобы получить сопротивление в 1 Ом, нужно взять 57 м такой проволоки.

Сопротивление проводника можно определить по формуле:

где r

– сопротивление проводника в омах;ρ – удельное сопротивление проводника;l – длина проводника в м;S – сечение проводника в мм².

Пример 1.

Определить сопротивление 200 м железной проволоки сечением 5 мм².

Пример 2.

Вычислить сопротивление 2 км алюминиевой проволоки сечением 2,5 мм².

Из формулы сопротивления легко можно определить длину, удельное сопротивление и сечение проводника.

Пример 3.

Для радиоприемника необходимо намотать сопротивление в 30 Ом из никелиновой проволоки сечением 0,21 мм². Определить необходимую длину проволоки.

Пример 4.

Определить сечение 20 м нихромовой проволоки, если сопротивление ее равно 25 Ом.

Пример 5.

Проволока сечением 0,5 мм² и длиной 40 м имеет сопротивление 16 Ом. Определить материал проволоки.

Материал проводника характеризует его удельное сопротивление.

По таблице удельных сопротивлений находим, что таким сопротивлением обладает свинец.

У некоторых металлов при нагревании на 100° сопротивление увеличивается на 40 – 50 %. Имеются сплавы, которые незначительно меняют свое сопротивление с нагревом. Некоторые специальные сплавы практически не меняют сопротивления при изменении температуры. Сопротивление металлических проводников при повышении температуры увеличивается, сопротивление электролитов (жидких проводников), угля и некоторых твердых веществ, наоборот, уменьшается.

Изменение сопротивления проводника при его нагревании, приходящееся на 1 Ом первоначального сопротивления и на 1° температуры, называется температурным коэффициентом сопротивления

и обозначается буквой α.

Если при температуре t

0 сопротивление проводника равноr 0 , а при температуреt равноr t , то температурный коэффициент сопротивления

Примечание.

Расчет по этой формуле можно производить лишь в определенном интервале температур (примерно до 200°C).

Приводим значения температурного коэффициента сопротивления α для некоторых металлов (таблица 2).

Таблица 2

Значения температурного коэффициента для некоторых металлов

Из формулы температурного коэффициента сопротивления определим r t

r t

=r 0 .

Пример 6.

Определить сопротивление железной проволоки, нагретой до 200°C, если сопротивление ее при 0°C было 100 Ом.

r t

=r 0 = 100 (1 + 0,0066 × 200) = 232 Ом.

Пример 7.

Термометр сопротивления, изготовленный из платиновой проволоки, в помещении с температурой 15°C имел сопротивление 20 Ом. Термометр поместили в печь и через некоторое время было измерено его сопротивление. Оно оказалось равным 29,6 Ом. Определить температуру в печи.

Соединение медных и алюминиевых проводов

В последнее время в быту и промышленности начало использоваться электрооборудование все более высокой мощности. Во времена СССР проводка изготавливалась в основном из дешевого алюминия. Новым требованиям ее эксплуатационные характеристики, к сожалению, уже не соответствуют. Поэтому сегодня в быту и в промышленности очень часто алюминиевые провода меняются на медные. Основным преимуществом последних, помимо тугоплавкости, является то, что при окислительном процессе их токопроводящие свойства не уменьшаются.

Часто при модернизации электросетей алюминиевые и медные провода приходится соединять. Делать это напрямую нельзя. Собственно, электропроводность алюминия и меди различается не слишком сильно. Но только у самих этих металлов. Окислительные же пленки у алюминия и меди свойства имеют неодинаковые. Из-за этого значительно снижается проводимость в месте соединения. Окислительная пленка у алюминия отличается гораздо большим сопротивлением, чем у меди. Поэтому соединение этих двух разновидностей проводников должно производиться исключительно через специальные переходники. Это могут быть, к примеру, зажимы, содержащие пасту, защищающую металлы от появления окиси. Данный вариант переходников обычно используется при соединении проводов на улице. В помещениях чаще применяются ответвительные сжимы. В их конструкцию входит специальная пластина, исключающая прямой контакт между алюминием и медью. При отсутствии таких проводников в бытовых условиях вместо скручивания проводов напрямую рекомендуется использовать шайбу и гайку в качестве промежуточного «мостика».

Газы

Газы выполняют роль диэлектрика и не могут проводить электроток. А для того чтобы он сформировался необходимы носители зарядов. В их роли выступают ионы, и они возникают за счет влияния внешних факторов.

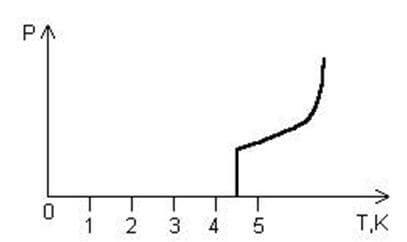
Зависимость можно рассмотреть на примере. Для опыта используется такая же конструкция, что и в предыдущем опыте, только проводники заменяются металлическими пластинами. Между ними должно быть небольшое пространство. Амперметр должен указывать на отсутствие тока. При помещении горелки между пластинами, прибор укажет ток, который проходит через газовую среду.

Ниже предоставлен график вольт-амперной характеристики газового разряда, где видно, что рост ионизации на первоначальном этапе возрастает, затем зависимость тока от напряжения остается неизменная (то есть при росте напряжения ток остается прежний) и резкий рост силы тока, который приводит к пробою диэлектрического слоя.

Рассмотрим проводимость газов на практике. Прохождение электрического тока в газах применяется в люминесцентных светильниках и лампах. В этом случае катод и анод, два электрода размещают в колбе, внутри которой есть инертный газ. Как зависит такое явление от газа? Когда лампа включается, две нити накала разогреваются, и создается термоэлектронная эмиссия. Внутри колба покрывается люминофором, который излучает свет, который мы видим. Как зависит ртуть от люминофора? Пары ртути при бомбардировании их электронами образуют инфракрасное излучение, которое в свою очередь излучает свет.

Если приложить напряжение между катодом и анодом, то возникает проводимость газов.

Свойства резистивных материалов

Удельное сопротивление металла зависит от температуры. Их значения приводится, как правило, для комнатной температуры (20°С). Изменение удельного сопротивления в результате изменения температуры характеризуется температурным коэффициентом.

Например, в термисторах (терморезисторах) это свойство используется для измерения температуры. С другой стороны, в точной электронике, это довольно нежелательный эффект. Металлопленочные резисторы имеют отличные свойства температурной стабильности. Это достигается не только за счет низкого удельного сопротивления материала, но и за счет механической конструкции самого резистора.

Много различных материалов и сплавов используются в производстве резисторов. Нихром (сплав никеля и хрома), из-за его высокого удельного сопротивления и устойчивости к окислению при высоких температурах, часто используют в качестве материала для изготовления проволочных резисторов. Недостатком его является то, что его невозможно паять. Константан, еще один популярный материал, легко паяется и имеет более низкий температурный коэффициент.

Таблица удельного электрического сопротивления некоторых металлов

Вид провода	ρ при 20℃, Ом-м
Серебряный	1,59×10⁻⁸
Медный	1,67×10⁻⁸
Золотой	2,35×10⁻⁸
Алюминиевый	2,65×10⁻⁸
Вольфрамовый	5,65×10⁻⁸
Никелевый	6,84×10⁻⁸
Железный	9,7×10⁻⁸
Платиновый	1,06×10⁻⁷
Стальной	1,6×10⁻⁷
Свинцовый	2,06×10⁻⁷
Дюралюминиевый	4,0×10⁻⁷
Нихромовый	1,05×10⁻⁶

Удельное сопротивление абсолютно независимо от формы и размеров проводника, однако варьируется в широком диапазоне при отклонении температуры от принятого за стандартное значения, равного 20 градусам Цельсия. Практическим электротехническим путем доказано, что увеличение температуры повышает сопротивляемость металлов течению тока, с обратной стороны — вместе со снижением температуры она снижается. Примерно подсчитать, насколько существенным будет изменение, можно с учетом того, что всем металлам присущ почти одинаковый уровень прироста убыли данной величины, в среднем составляющий 0,4% на 1°С.

Вам это будет интересно Фен для паяния

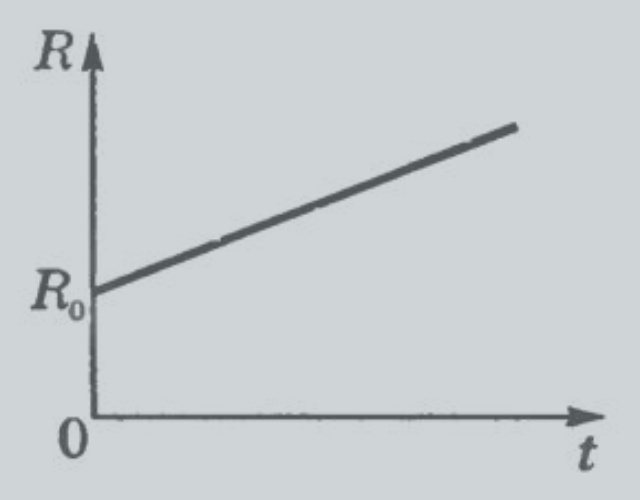
График сопротивления

Если же данный показатель нужно определить точно, то можно воспользоваться этой формулой:

ρ = ρ0 x (1 + α x (t — t))

, где ρ и ρ0 — соответственно удельные сопротивления при температурах t и t (20°С, табличное значение), α — температурный коэффициент сопротивления.

Вид провода	α
Никелевый	0,005866
Железный	0,005671
Молибденовый	0,004579
Вольфрамовый	0,004403
Алюминиевый	0,004308
Медный	0,004041
Серебряный	0,003819
Платиновый	0,003729
Золотой	0,003715
Цинковый	0,003847
Стальной	0,003
Нихромовый	0,00017

Так, к примеру, найдя в таблицах удельное сопротивление меди при 20 градусах Цельсия и ее температурный коэффициент, можно вычислить, что при нагреве до 100℃ ее сопротивление вырастет на 32%. Практически то же самое будет происходить с удельным сопротивлением алюминиевого кабеля с тем же коэффициентом (0,004). А вот удельное сопротивление стали повысится менее значительно — на 24%.

Нагрев

С увеличением температуры проводник насыщается тепловой энергией, передающейся всем атомам вещества. Этим обуславливается повышение интенсивности их теплового движения. Последний фактор и приводит к повышению сопротивляемости движению свободных электронов в определенном направлении, поскольку возрастает вероятность встречи свободных электронов с атомами. Когда температура снижается, меньшее количество атомов может препятствовать направленному движению электронов, следовательно, происходит обратное. В результате колоссального спада температуры возникает интереснейшее явление, называемое «сверхпроводимостью металлов»: сопротивляемость уменьшается до нуля в условиях, близких к абсолютному нулю (-273,15℃). В таких кондициях атомы металла замирают на своих позициях, и электроны движутся без каких-либо препятствий.

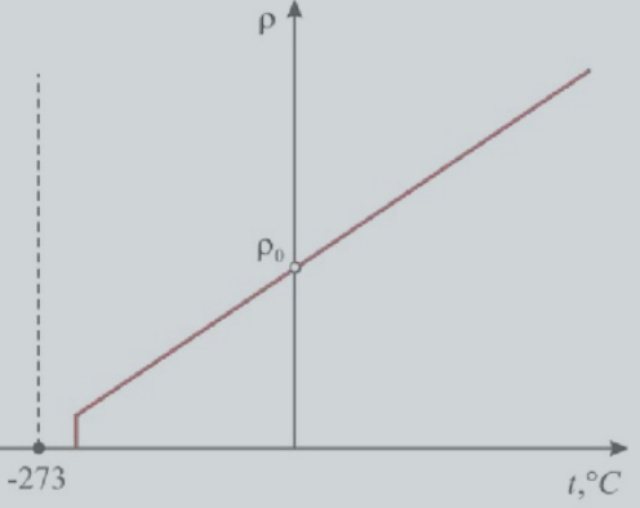
Сверхпроводимость

Железо как проводник в электротехнике

Железо — самый распространенный в природе и технике металл (после водорода, который металлом тоже является). Он и самый дешевый, и имеет прекрасные прочностные характеристики, поэтому применяется повсюду как основа прочности различных конструкций.

В электротехнике в качестве проводника железо используется в виде стальных гибких проводов там, где нужна физическая прочность и гибкость, а нужное сопротивление может быть достигнуто за счет соответствующего сечения.

Имея таблицу удельных сопротивлений различных металлов и сплавов, можно посчитать сечения проводов, выполненных из разных проводников.

В качестве примера попробуем найти электрически эквивалентное сечение проводников из разных материалов: проволоки медной, вольфрамовой, никелиновой и железной. За исходную возьмем проволоку алюминиевую сечением 2,5 мм.

Нам нужно, чтобы на длине в 1 м сопротивление провода из всех этих металлов равнялось сопротивлению исходной. Сопротивление алюминия на 1 м длины и 2,5 мм сечения будет равно

Где R – сопротивление, ρ – удельное сопротивление металла из таблицы, S – площадь сечения, L – длина.

Подставив исходные значения, получим сопротивление метрового куска провода алюминия в омах.

После этого разрешим формулу относительно S

Будем подставлять значения из таблицы и получать площади сечений для разных металлов.

Так как удельное сопротивление в таблице измерено на проводе длиной в 1 м, в микроомах на 1 мм 2 сечения, то у нас и получилось оно в микроомах. Чтобы получить его в омах, нужно умножить значение на 10 -6 . Но число ом с 6 нулями после запятой нам получать совсем не обязательно, так как конечный результат все равно находим в мм 2 .

Как видим, сопротивление железа достаточно большое, проволока получается толстая.

Но существуют материалы, у которых оно еще больше, например, никелин или константан.

Про закон Ома многие слышали, но не все знают, что это такое. Изучение начинается со школьного курса физики. Более подробно проходят на физфаке и электродинамике. Рядовому обывателю эти знания маловероятно пригодятся, но они необходимы для общего развития, а кому-то для будущей профессии. С другой стороны, элементарные знания об электричестве, его устройстве, особенностей в домашних условиях помогут предостеречь себя от беды. Недаром закон Ома называют основным законом электричества. Домашнему мастеру нужно обладать знаниями в области электричества, чтобы не допустить перенапряжения, что может повлечь увеличению нагрузки и возникновению пожара.

Описание

Закон Ома гласит, что, когда источник напряжения (V) подается между двумя точками в цепи, между ними будет протекать электрический ток (I), вызванный наличием разности потенциалов между этими двумя точками. Количество протекающего электрического тока ограничено величиной присутствующего сопротивления (R). Другими словами, напряжение стимулирует протекание тока (движение заряда), но это сопротивление препятствует этому.

Мы всегда измеряем электрическое сопротивление в Омах, где Ом обозначается греческой буквой Омега, Ω. Так, например: 50 Ом, 10 кОм или 4,7 МОм и т.д. Проводники (например, провода и кабели) обычно имеют очень низкие значения сопротивления (менее 0,1 Ом), и, таким образом, мы можем пренебречь ими, как мы предполагаем в расчетах анализа цепи, что провода имеют ноль сопротивление. С другой стороны, изоляторы (например, пластиковые или воздушные), как правило, имеют очень высокие значения сопротивления (более 50 МОм), поэтому мы можем их игнорировать и для анализа цепи, поскольку их значение слишком велико.

Но электрическое сопротивление между двумя точками может зависеть от многих факторов, таких как длина проводников, площадь их поперечного сечения, температура, а также фактический материал, из которого он изготовлен. Например, давайте предположим, что у нас есть кусок провода (проводник), который имеет длину L, площадь поперечного сечения A и сопротивление R, как показано ниже.

Электрическое сопротивление R этого простого проводника является функцией его длины, L и площади поперечного сечения A. Закон Ома говорит нам, что для данного сопротивления R ток, протекающий через проводник, пропорционален приложенному напряжению, поскольку I = V / R. Теперь предположим, что мы соединяем два одинаковых проводника вместе в последовательной комбинации, как показано на рисунке.

Здесь, соединив два проводника вместе в последовательной комбинации, то есть, к концу, мы фактически удвоили общую длину проводника (2L), в то время как площадь поперечного сечения A остается точно такой же, как и раньше. Но помимо удвоения длины, мы также удвоили общее сопротивление проводника, дав 2R как: 1R + 1R = 2R.

Таким образом , мы можем видеть , что сопротивление проводника пропорционально его длину, то есть: R ∝ L. Другими словами, мы ожидаем, что электрическое сопротивление проводника (или провода) будет пропорционально больше, чем оно длиннее.

Отметим также, что, удваивая длину и, следовательно, сопротивление проводника (2R), чтобы заставить тот же ток I, чтобы течь через проводник, как и раньше, нам нужно удвоить (увеличить) приложенное напряжение I = (2 В) / (2R). Далее предположим, что мы соединяем два идентичных проводника вместе в параллельной комбинации, как показано.

Здесь, соединяя два проводника в параллельную комбинацию, мы фактически удвоили общую площадь, дающую 2А, в то время как длина проводников L остается такой же, как у исходного одиночного проводника. Но помимо удвоения площади, путем параллельного соединения двух проводников мы фактически вдвое сократили общее сопротивление проводника, получив 1 / 2R, поскольку теперь каждая половина тока протекает через каждую ветвь проводника.

Таким образом, сопротивление проводника обратно пропорционально его площади, то есть: R 1 / ∝ A или R ∝ 1 / A. Другими словами, мы ожидаем, что электрическое сопротивление проводника (или провода) будет пропорционально меньше, чем больше его площадь поперечного сечения.

Кроме того, удваивая площадь и, следовательно, вдвое увеличивая суммарное сопротивление ветви проводника (1 / 2R), для того же тока, чтобы I протекал через параллельную ветвь провода, как раньше, нам нужно только наполовину уменьшить приложенное напряжение I = (1 / 2V) / (1 / 2R).

Надеемся, мы увидим, что сопротивление проводника прямо пропорционально длине (L) проводника, то есть: R ∝ L, и обратно пропорционально его площади (A), R ∝ 1 / A. Таким образом, мы можем правильно сказать, что сопротивление это:

Металлы

Как температура влияет на металлы? Чтобы узнать эту зависимость был проведен такой эксперимент: батарейку, амперметр, проволоку и горелку соединяют между собой с помощью проводов. Затем необходимо замерить показание тока в цепи. После того как показания были сняты, нужно горелку поднести к проволоке и нагреть ее. При нагревании проволоки видно, что сопротивление возрастает, а проводимость металла уменьшается.

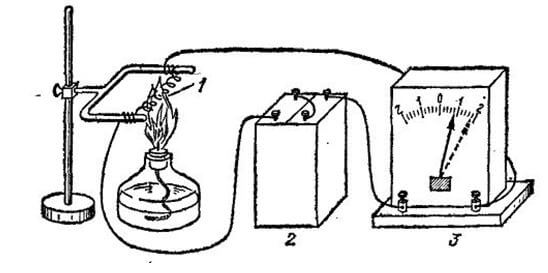
где:

Металлическая проволока
Батарея
Амперметр

Также нужно уделить внимание такому свойству, как сверхпроводимость. Если условия окружающей среды обычные, то охлаждаясь, проводники уменьшают свое сопротивление

График ниже показывает, как зависит температура и удельное сопротивление в ртути.

При нагреве сопротивление увеличивается или уменьшается