Единицы измерения электрического заряда

Содержание:

А точечная нагрузкаВ контексте электромагнетизма это тот электрический заряд настолько малых размеров, что его можно рассматривать как точку. Например, элементарные частицы, обладающие электрическим зарядом, протон и электрон, настолько малы, что их размеры можно не указывать во многих приложениях. Учет того, что заряд является точечно-ориентированным, значительно упрощает вычисление его взаимодействий и понимание электрических свойств материи.

Точечным зарядом могут быть не только элементарные частицы. Это также могут быть ионизированные молекулы, заряженные сферы, которые Чарльз А. Кулон (1736–1806) использовал в своих экспериментах, и даже сама Земля. Все можно считать точечными зарядами, если мы видим их на расстояниях, намного превышающих размер объекта.

Поскольку все тела состоят из элементарных частиц, электрический заряд является неотъемлемым свойством материи, как и масса. Вы не можете иметь электрон без массы, а также без заряда.

Работа поля точечного заряда.

Более правильно название данного раздела должно звучать
так: «Работа электростатического поля, созданного точечным зарядом Q, по перемещению точечного заряда
q из точки 1 в точку 2». Но мы с вами и так понимаем, о чем речь.

Начало координат выбрано в точке, в которой находится заряд Q. Из рис.6.2 видно, что
. Учитывая, что

,

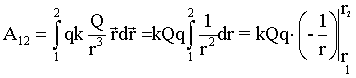(6.3)

Можно сделать вывод, что работа электростатического
поля, созданного точечным зарядом, а также любого другого центрально-симметричного
поля, не зависит от формы пути, а определяется только начальным и конечным положением.

очевидно, что работа поля при перемещении заряда по замкнутому контуру равна 0.

(6.4)

Гравитация и электричество

Эти две силы имеют одинаковую математическую форму. Конечно, они различаются величиной постоянной пропорциональности и тем, что гравитация работает с массами, а электричество работает с зарядами.

Но важно то, что оба значения зависят от обратной величины квадрата расстояния. Существует уникальный тип массы, и он считается положительным, поэтому сила гравитации всегда притягивает, а заряды могут быть положительными или отрицательными

По этой причине электрические силы могут быть притягивающими или отталкивающими, в зависимости от случая

Существует уникальный тип массы, и он считается положительным, поэтому сила гравитации всегда притягивает, а заряды могут быть положительными или отрицательными. По этой причине электрические силы могут быть притягивающими или отталкивающими, в зависимости от случая.

И у нас есть деталь, вытекающая из вышеизложенного: все объекты в свободном падении имеют одинаковое ускорение, пока они находятся близко к поверхности Земли.

Но если, например, мы выпустим протон и электрон около заряженной плоскости, электрон будет иметь гораздо большее ускорение, чем протон. Кроме того, ускорения будут иметь противоположные направления.

Наконец, электрический заряд квантуется, как и было сказано. Это означает, что мы можем найти заряды в 2,3 или 4 раза больше, чем у электрона, или у протона, но никогда не в 1,5 раза больше этого заряда. С другой стороны, массы не кратны какой-то одной массе.

В мире субатомных частиц электрическая сила больше силы тяжести. Однако в макроскопических масштабах сила тяжести является преобладающей. Куда? На уровне планет, солнечной системы, галактики и многого другого.

Физика для средней школы

Точечный и распределенный заряды

Идеальной физической моделью заряда в электростатике является точечный заряд.

Точечным зарядом называется заряд, сосредоточенный на теле, размерами которого можно пренебречь по сравнению с расстоянием до других тел или до рассматриваемой точки поля. Иными словами, точечный заряд — это материальная точка, которая имеет электрический заряд.

Если заряженное тело настолько велико, что его нельзя рассматривать как точечный заряд, то в этом случае необходимо знать распределение зарядов внутри тела.

Выделим внутри заряженного тела малый объем и обозначим через электрический заряд, находящийся в этом объеме. Предел отношения , когда объем неограниченно уменьшается, называют объемной плотностью электрического заряда в данной точке. Обозначают ее буквой :

Единицей объемной плотности заряда в СИ является кулон на кубический метр (Кл/м3).

В случае неравномерно заряженного тела плотность различна в разных точках. Распределение заряда в объеме тела задано, если известно как функция координат.

В металлических телах заряды распределяются только внутри тонкого слоя, прилегающего к поверхности. В этом случае удобно пользоваться поверхностной плотностью заряда , которая представляет собой предел отношения заряда к площади поверхности, по которой распределен этот заряд:

где — заряд, находящийся на участке поверхности площадью .

Следовательно, поверхностная плотность заряда измеряется зарядом, приходящимся на единицу поверхности тела. Распределение зарядов по поверхности описывается зависимостью поверхностной плотности (x, y, z) от координат точек поверхности.

Единицей поверхностной плотности заряда в СИ является кулон на квадратный метр (Кл/м2).

В том случае, если заряженное тело по форме представляет собой нить (диаметр поперечного сечения тела много меньше его длины , удобно использовать линейную плотность заряда

где — заряд, находящийся на длине тела.

Единицей линейной плотности заряда в СИ является кулон на метр (Кл/м).

Если известно распределение зарядов внутри тела, то можно вычислить напряженность электростатического поля, создаваемого этим телом. Для этого заряженное тело мысленно разбивают на бесконечно малые части и, рассматривая их как точечные заряды, вычисляют напряженность поля, создаваемую отдельными частями тела. Суммарную напряженность поля находят затем суммированием полей, создаваемых отдельными частями тела, т.е.

Как вычислять с помощью законов

Поскольку q и Q являются скалярными единицами, вычислить их с помощью законов можно через точные формулы, выведенные известными учеными-физиками. К примеру, в соответствии с законом Кулона, можно найти величину и силовое направление взаимодействия заряженных частиц между несколькими неподвижными телами.

Вам это будет интересно Особенности обозначения радиодеталей на схеме

Закон сохранения

Все элементарные частицы подразделяются на нейтральные или заряженные. Они вступают во взаимодействие друг с другом внутри электромагнитного поля. Частицы, которые имеют одноименный электрон, отталкиваются, а разноименный – притягиваются. В первом случае наблюдается избыток электронов, а во втором – их недостаток. Оба типа частиц заряжаются посредством электризации. На практике, при возникновении данного явления, заряженные частицы равны по модулю, несмотря на противоположность знаков. Когда разные частицы притягиваются, то между ними происходит электризация и сохранение электрона. При этом, сумма всех изолированных системных частиц не изменяется, то есть, q + q + q…= const.

Закон сохранения

Закон Кулона

Выше было сказано, что электрические заряженные микрочастицы бывают как положительными, так и отрицательными, а их наличие подтверждается силовым взаимодействием, которое с помощью экспериментов на весах описал в 1785 году О. Кулон, создав свой физико-математический закон.

Закон Кулона представляет собой физическую закономерность, которая описывает взаимодействие наэлектризованных частиц между не электризованными, в зависимости от промежутка между ними. В соответствии с этой формулировкой, чем больше электронов имеет частица, тем ближе она расположена к другой элементарной единице заряда, и, соответственно, сила возрастает.

Обратите внимание! При увеличении расстояния между частицами, сал их взаимодействия неизменно убывает. В математической формуле это выглядит так: F1 = F2 = K*(q1*q2/r2), где q1 и q2 считаются модулями заряженных микрочастиц, k является коэффициентом пропорциональности, который зависит от системного выбора единицы, а r — расстоянием

Закон Кулона

Главная
Справочник
Законы
Закон Кулона

Закон Кулона количественно описывает взаимодействие заряженных тел. Он является фундаментальным законом, то есть установлен при помощи эксперимента и не следует ни из какого другого закона природы. Он сформулирован для неподвижных точечных зарядов в вакууме. В реальности точечных зарядов не существует, но такими можно считать заряды, размеры которых значительно меньше расстояния между ними. Сила взаимодействия в воздухе почти не отличается от силы взаимодействия в вакууме (она слабее менее чем на одну тысячную).

Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.

Впервые закон взаимодействия неподвижных зарядов был открыт французским физиком Ш. Кулоном в 1785 г. В опытах Кулона измерялось взаимодействие между шариками, размеры которых много меньше расстояния между ними. Такие заряженные тела принято называть точечными зарядами.

На основании многочисленных опытов Кулон установил следующий закон:

Сила взаимодействия двух неподвижных точечных электрических зарядов в вакууме прямо пропорциональна произведению их модулей и обратно пропорциональна квадрату расстояния между ними. Она направлена вдоль прямой, соединяющей заряды, и является силой притяжения, если заряды разноименные, и силой отталкивания, если заряды одноименные.

Если обозначить модули зарядов через |q

1| и |q 2|, то закон Кулона можно записать в следующей форме:

Коэффициент пропорциональности k в законе Кулона зависит от выбора системы единиц.

Полная формула закона Кулона:

Где :

\( F \) — Сила Кулона

\( q_1 q_2 \) — Электрический заряд тела

\( r \) — Расстояние между зарядами

\( \varepsilon_0 = 8,85*10^{-12} \) — Электрическая постоянная

\( \varepsilon \) — Диэлектрическая проницаемость среды

\( k = 9*10^9 \) — Коэффициент пропорциональности в законе Кулона

Силы взаимодействия подчиняются третьему закону Ньютона: \( \vec{F}_{12}=\vec{F}_{21} \) . Они являются силами отталкивания при одинаковых знаках зарядов и силами притяжения при разных знаках.

Электрический заряд обычно обозначается буквами q или Q.

Совокупность всех известных экспериментальных фактов позволяет сделать следующие выводы:

Существует два рода электрических зарядов, условно названных положительными и отрицательными.
Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.
Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.

Взаимодействие неподвижных электрических зарядов называют электростатическим или кулоновским взаимодействием. Раздел электродинамики, изучающий кулоновское взаимодействие, называют электростатикой.

Закон Кулона справедлив для точечных заряженных тел. Практически закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними.

Отметим, чтоб выполнялся закон Кулона необходимо 3 условия:

Точечность зарядов — то есть расстояние между заряженными телами много больше их размеров.
Неподвижность зарядов. Иначе вступают в силу дополнительные эффекты: магнитное поле движущегося заряда и соответствующая ему дополнительная сила Лоренца, действующая на другой движущийся заряд .
Взаимодействие зарядов в вакууме.

В Международной системе СИ за единицу заряда принят кулон (Кл).

Кулон – это заряд, проходящий за 1 с через поперечное сечение проводника при силе тока 1 А. Единица силы тока (Ампер) в СИ является наряду с единицами длины, времени и массы основной единицей измерения.

ЗаконыФормулы Физика Теория Электричество Закон

Потенциал электрического поля. Разность потенциалов

Потенциал – скалярная физическая величина, равная отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда.

Обозначение – \( \varphi \), единица измерения в СИ – вольт (В).

Потенциал \( \varphi \) является энергетической характеристикой электростатического поля.

Разность потенциалов численно равна работе, которую совершает электрическая сила при перемещении единичного положительного заряда между двумя точками поля:

Обозначение – \( \Delta\varphi \), единица измерения в СИ – вольт (В).

Иногда разность потенциалов обозначают буквой \( U \) и называют напряжением.

Важно!
Разность потенциалов \( \Delta\varphi=\varphi_1-\varphi_2 \), а не изменение потенциала \( \Delta\varphi=\varphi_2-\varphi_1 \). Тогда работа электростатического поля равна:. Важно!
Эта формула позволяет вычислить работу электростатических сил в любом поле

В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки

Важно!
Эта формула позволяет вычислить работу электростатических сил в любом поле. В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки. В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность

В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность

В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки. В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Потенциал поля точечного заряда \( q \) в точке, удаленной от него на расстояние \( r \), вычисляется по формуле:

Для наглядного представления электрического поля используют эквипотенциальные поверхности.

Важно!
Внутри проводящего шара потенциал всех точек внутри шара равен потенциалу поверхности шара и вычисляется по формуле потенциала точечного заряда (\( r =R \), где \( R \) – радиус шара). Напряженность поля внутри шара равна нулю. Эквипотенциальной поверхностью, или поверхностью равного потенциала, называется поверхность, во всех точках которой потенциал имеет одинаковое значение

Эквипотенциальной поверхностью, или поверхностью равного потенциала, называется поверхность, во всех точках которой потенциал имеет одинаковое значение.

Свойства эквипотенциальных поверхностей

Вектор напряженности перпендикулярен эквипотенциальным поверхностям и направлен в сторону убывания потенциала.
Работа по перемещению заряда по эквипотенциальной поверхности равна нулю.

В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей. Для точечного заряда эквипотенциальные поверхности представляют собой концентрические окружности.

Разность потенциалов и напряженность связаны формулой:

Из принципа суперпозиции полей следует принцип суперпозиции потенциалов:

Потенциал результирующего поля равен сумме потенциалов полей отдельных зарядов.

Важно!
Потенциалы складываются алгебраически, а напряженности – по правилу сложения векторов. Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил. Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил

Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил.

Алгоритм решения таких задач:

установить характер и особенности электростатических взаимодействий объектов системы;
ввести характеристики (силовые и энергетические) этих взаимодействий, сделать рисунок;
записать законы сохранения и движения для объектов;
выразить энергию электростатического взаимодействия через заряды, потенциалы, напряженности;
составить систему уравнений и решить ее относительно искомой величины;
проверить решение.

Формула заряда конденсатора

Для выполнения зарядки, конденсатор должен быть подключен к цепи постоянного тока. С этой целью может использоваться генератор. У каждого генератора имеется внутреннее сопротивление. При замыкании цепи происходит зарядка конденсатора. Между его обкладками появляется напряжение, равное электродвижущей силе генератора: Uc = E.

Обкладка, подключенная к положительному полюсу генератора, заряжается положительно (+q), а другая обкладка получает равнозначный заряд с отрицательной величиной (- q). Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc.

В процессе зарядки одна из обкладок конденсатора приобретает, а другая теряет определенное количество электронов. Они переносятся по внешней цепи под влиянием электродвижущей силы генератора. Такое перемещение является электрическим током, известным еще как зарядный емкостной ток (Iзар).

Свойства

Насколько нам известно сегодня, существует два типа электрического заряда: положительный и отрицательный. Электроны имеют отрицательный заряд, а протоны — положительный.

Заряды одного знака отталкиваются, а заряды противоположного знака — притягиваются. Это справедливо для любого типа электрического заряда, точечного или распределенного по объекту измеримых размеров.

Более того, тщательные эксперименты показали, что заряд протона и электрона имеет одинаковую величину.

Еще один очень важный момент, который следует учитывать, — это квантование электрического заряда. На сегодняшний день не обнаружено изолированных электрических зарядов величиной меньше заряда электрона. Все они кратны этому.

Наконец, электрический заряд сохраняется. Другими словами, электрический заряд не создается и не разрушается, но он может передаваться от одного объекта к другому. Таким образом, если система изолирована, общая нагрузка остается постоянной.

Линии напряженности

Электрическое поле нельзя увидеть невооруженным глазом, но можно изобразить с помощью линий напряженности. Графически это будут непрерывные прямые, которые связывают заряженные объекты. Условная точка начала такой прямой — на положительном заряде, а конечная точка — на отрицательном.

Линии напряженности — это прямые, которые совпадают с силовыми линиями в системе из положительного и отрицательного зарядов. Касательные к ним в каждой точке электрического поля имеют то же направление, что и напряженность этого поля.

При графическом изображении силовых линий можно передать не только направление, но и величину напряженности электрического поля (разумеется, условно). В местах, где модуль напряженности выше, принято делать более густой рисунок линий. Есть и случаи, когда густота линий не меняется — это бывает при изображении однородного поля.

Однородное электрическое поле создается разноименными зарядами с одинаковым модулем, расположенными на двух металлических пластинах. Линии напряженности между этими зарядами представляют собой параллельные прямые всюду, за исключением краев пластин и пространства за ними.

Потенциал. Эквипотенциальные поверхности.

В механике взаимодействие тел характеризует силой или потенциальной энергией. Электрическое поле, которое обеспечивает взаимодействие между электрически заряженными телами, также характеризуют двумя величинами. Напряженность электрического поля — это силовая характеристика. Теперь введем энергетическую характеристику — потенциал. С помощью этой величины можно будет сравнивать между собой любые точки электрического поля. Таким образом, потенциал как характеристика поля должен зависеть от значения заряда, содержащегося в этих точках. Поделим обе части формулы A = W₁ — W₂ на заряд q, получим

Отношение W/q не зависит от значения заряда и принимается за энергетическую характеристику, которую называют потенциалом поля в данной точке. Обозначают потенциал буквой φ.

Потенциал электрического поля φ — скалярная энергетическая характеристика поля, которая определяется отношением потенциальной энергии W положительного заряда q в данной точке поля к величине этого заряда:

Единица потенциала — вольт:

Подобно потенциальной энергии значения потенциала в данной точке зависит от выбора нулевого уровня для отсчета потенциала. Чаще всего в электродинамике за нулевой уровень берут потенциал точки, лежащей в бесконечности, а в электротехнике — на поверхности Земли.

С введением потенциала формулу для определения работы по перемещению заряда между точками 1 и 2 можно записать в виде

Поскольку при перемещении положительного заряда в направлении вектора напряженности электрическое поле выполняет положительную работу A = q (φ₁ — φ₂ )> 0, то потенциал φ₁ больше чем потенциал φ₂ . Таким образом, напряженность электрического поля направлена в сторону уменьшения потенциала.

Если заряд перемещать с определенной точки поля в бесконечность, то работа A = q (φ — φ_∞ ). Поскольку φ_∞ = 0, то A = qφ. Таким образом, величина потенциала φ определенной точки поля определяется работой, которую выполняет электрическое поле, перемещая единичный положительный заряд из этой точки в бесконечность,

Если электрическое поле создается точечным зарядом q, то в точке, лежащей на расстоянии r от него, потенциал вычисляют по формуле

По этой формуле рассчитывают и потенциал поля заряженного шара. В таком случае r — это расстояние от центра шара до выбранной точки поля. С этой формулы видно, что на одинаковых расстояниях от точечного заряда, который создает поле, потенциал одинаков. Все эти точки лежат на поверхности сферы, описанной радиусом r вокруг точечного заряда. Такую сферу называют эквипотенциальной поверхностью.

Эквипотенциальные поверхности — геометрическое место точек в электрическом поле, которые имеют одинаковый потенциал, — один из методов наглядного изображения электрических полей.

Эквипотенциальные поверхности электрических полей, созданных точечными зарядами разных знаков

Силовые линии всегда перпендикулярны эквипотенциальных поверхностей. Это означает, что работа сил поля по перемещению заряда по эквипотенциальной поверхности равна нулю.

В случае наложения электрических полей, созданных несколькими зарядами, потенциал электрического поля равен алгебраической сумме потенциалов полей, созданных отдельными зарядами, φ = φ₁ + φ₂ + φ₃ . Эквипотенциальные поверхности таких систем имеют сложную форму. Например, для системы из двух одинаковых по значению одноименных зарядов эквипотенциальные поверхности имеют вид, изображенный на рисунке. Эквипотенциальные поверхности однородного поля явлются плоскостями.

Эквипотенциальные поверхности: а — поля двух одинаковых зарядов б — однородного поля

Как вычислять с помощью законов

Вам это будет интересно Расчет эквивалентного сопротивления

Закон сохранения

Закон Кулона

Элементарные частицы

Что же происходит с телами при электризации? Представьте себе два одинаковых металлических шара, но только один из них заряжен отрицательно, а другой не заряжен (см. рис. 10).

Рис. 10. Заряженный и незаряженный шары

Известно, что все тела состоят из атомов, а те, в свою очередь, состоят из протонов, нейтронов, электронов (см. рис. 11).

Рис. 11. Атом

Протоны заряжены положительно, электроны – отрицательно. Будем называть их элементарными зарядами, то есть неделимыми. Так вот, в большинстве случаев в атоме количество протонов равняется количеству электронов и получается, что они полностью компенсируют друг друга и в целом атом нейтрален

Важно понимать, что в атоме заряды никуда не исчезают, там по-прежнему есть положительные и отрицательные частицы, просто их действие на далекие предметы полностью компенсируется (см. рис. 12)

12).

Рис. 12. Действие частиц компенсировано

А вот в шаре, заряженном отрицательно, электронов больше, чем протонов, поэтому в целом в теле количество отрицательных элементарных зарядов больше, чем количество положительных элементарных зарядов, и тело заряжено отрицательно (см. рис. 13).

Рис. 13. Количество электронов в заряженном шаре

Заряд макроскопического тела (состоящего из большого количества атомов) – это величина, показывающая разность между положительными и отрицательными зарядами в теле. Если это количество одинаково, то заряд нулевой. Величина элементарного заряда известна и равна . Соответственно, заряд протона договорились считать положительным , а заряд электрона – отрицательным .

Что же происходит при трении тел друг о друга, например пластика о шерсть? Электроны с внешних оболочек атомов, входящих в состав шерсти, «перепрыгивают» на пластмассу (см. рис. 14).

Рис. 14. Движение электронов при трении

Получается, что в шерсти становится меньше отрицательных электронов и она заряжается положительно, а пластмасса – отрицательно, так как в ней появляется избыточное количество электронов. Можно даже сказать: если при контакте заряд одного тела увеличивается, то у другого уменьшается.

Что касается искр между людьми, то это происходит, если хотя бы один человек «заряжен» (допустим, человек ходил по шерстяному ковру, при трении подошвами по нему), и если другой человек не заряжен также, то заряд будет перетекать с одного человека на другого, иногда это перетекание может быть даже по воздуху, в таком случае и появляется искра. Стоит отметить, что искра появляется только благодаря движению электронов, протоны находятся в ядрах атомов, они менее подвижны и не могут покидать атомов отличие от электронов.

Зарядить тело можно и без контакта – через влияние электрическим полем. Представьте себе незаряженный шар, к которому подносят положительно заряженную палочку – разноименные заряды притягиваются, поэтому электроны, которые были в шаре, притянутся к положительно заряженной палочке и скопятся в той части шара, которая ближе к ней (см. рис. 15).

Рис. 15. Влияние положительно заряженной палочки на электроны

Почему незаряженные частицы фольги притягиваются к заряженной расческе?

Оказывается, незаряженный кусочек фольги будет притягиваться к заряженной расческе. Как же так? В целом кусочек фольги электрически нейтрален. Давайте посмотрим, что произойдет, если мы поднесем отрицательно заряженную расческу к кусочку фольги – отрицательно заряженная расческа притягивает к себе положительный заряд и отталкивает отрицательный. Поэтому электроны отодвинутся дальше от границы, а сторона, которая находится ближе к расческе, будет заряжена положительно (см. рис. 16) и притяжение будет сильнее, чем отталкивание, потому что положительная часть фольги находится ближе к расческе.

Рис. 16. Расположение электронов в фольге при поднесении расчески

Основные электрические величины

Содержание:

Работа поля точечного заряда.

Гравитация и электричество

Физика для средней школы

Точечный и распределенный заряды

Как вычислять с помощью законов

Закон сохранения

Закон Кулона

Закон Кулона

Потенциал электрического поля. Разность потенциалов

Формула заряда конденсатора

Свойства

Линии напряженности

Потенциал. Эквипотенциальные поверхности.

Как вычислять с помощью законов

Закон сохранения

Закон Кулона

Элементарные частицы

Похожие записи: