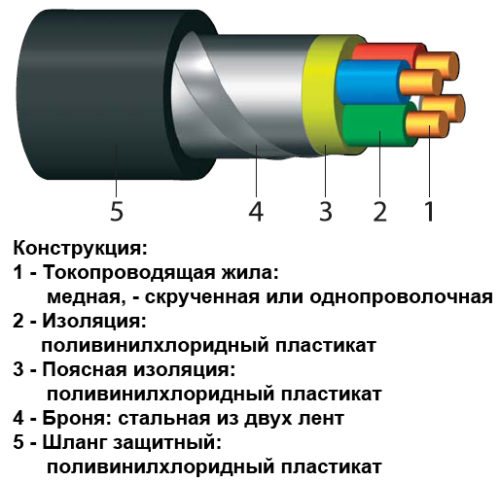
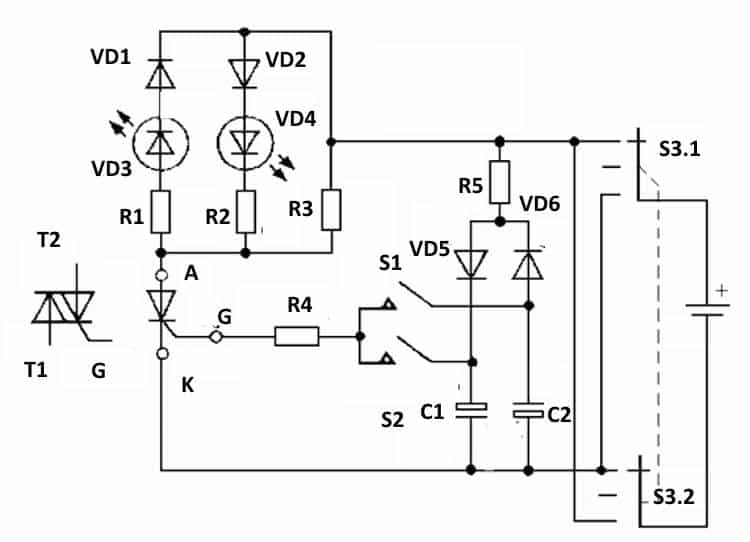
Логические функции на области числовых значений
Алгебра чисел пересекается с алгеброй логики в тех случаях, когда приходится проверять принадлежность значений алгебраических выражений некоторому множеству. Например, принадлежность значения числовой переменной X множеству положительных чисел выражается через высказывание: «X больше нуля». Символически это записывается так: Х > 0. В алгебре такое выражение называют неравенством. В логике — отношением.
Отношение X > О может быть истинным или ложным. Если X — положительная величина, то оно истинно, если отрицательная, то ложно. В общем виде отношение имеет следующую структуру:
<выражение 1> <знак отношения> <выражение 2>
Здесь выражения 1 и 2 — некоторые математические выражения, принимающие числовые значения. В частном случае выражение может представлять собой одну константу или одну переменную величину. Знаки отношений могут быть следующими:
= — равно;
≠ — не равно;
> — больше или равно;
≤ — меньше или равно;
> — больше;
< — меньше.
Например:
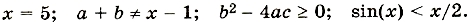
Итак, отношение — это простое высказывание, а значит, логическая величина. Оно может быть как постоянной: 5 > 0 — всегда ИСТИНА, 3 ≠ 6 : 2 — всегда ЛОЖЬ; так и переменной: а < Ь, х + 1 = с — d. Если в отношение входят переменные числовые величины, то и значение отношения будет логической переменной.
Отношение можно рассматривать как логическую функцию от числовых аргументов. Например: F(x) = (х > 0) или Р(х, у) = (х < у). Аргументы определены на бесконечном множестве действительных чисел, а значения функции — на множестве, состоящем из двух логических величин: ИСТИНА, ЛОЖЬ.
Логические функции от числовых аргументов еще называют термином предикат. В алгоритмах предикаты играют роль условий, по которым строятся ветвления и циклы. Предикаты могут быть как простыми логическими функциями, не содержащими логических операций, так и сложными, содержащими логические операции.
Пример 1. Записать предикат (логическую функцию) от двух вещественных аргументов X и У, который будет принимать значение ИСТИНА, если точка на координатной плоскости с координатами X и У лежит внутри единичной окружности с центром в начале координат (рис. 3.12).
Рис. 3.12
Из геометрических соображений понятно, что для всех точек, лежащих внутри единичной окружности, будет истинным значение следующей логической функции:
Для значений координат точек, лежащих на окружности и вне ее, значение функции F будет ложным.
Пример 2. Записать предикат, который будет принимать значение ИСТИНА, если точка на координатной плоскости с координатами X и У лежит внутри кольца с центром в начале координат, и радиусами R1 и R2.
Поскольку значения R1 и R2 — переменные величины, искомая логическая функция будет иметь четыре аргумента: X, У, R1, R2. Возможны две ситуации:
-
R12 < X2 + У2 < R22 и Rl < R2: R1 — внутренний радиус, R2 — внешний радиус;
- R22 < X2 + У2 < R12 и R2 < R1: R2 — внутренний радиус, R1 — внешний радиус.
Объединив дизъюнкцией оба этих утверждения и записав их по правилам алгебры логики, получим следующую логическую функцию:
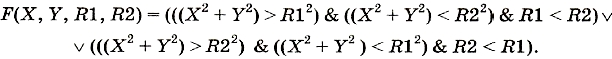
Пример 3. Записать предикат, который будет принимать значение ИСТИНА, если точка на координатной плоскости с координатами X и У лежит внутри фигуры, ограниченной жирными линиями на рис. 3.13.
Рис. 3.13
Фигура ограничена тремя границами, описываемыми уравнениями:
У = -X — левая граница, линейная функция;
У = 1 — верхняя граница, константа;
У = X2 — правая граница, парабола.
Рассматриваемая область есть пересечение трех полуплоскостей, описываемых неравенствами:
Во внутренних точках все эти три отношения являются одновременно истинными. Поэтому искомый предикат имеет вид:
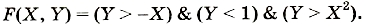
Законы алгебры логики
Имеется большое количество правил в данной сфере деятельности, но сегодня будет рассмотрено несколько основных.
Переместительный закон — предназначен для процесса сложения и вычитания. Суть данного правила в том, что обозначения А и В в операциях дизъюнкции и конъюнкции можно менять.
Сочетательный закон — применяется, когда есть или только операция дизъюнкции, или только операция конъюнкции. Тогда можно обходиться без скобок или хаотично ставить скобки.
Распределительный закон — имеется два типа данного правила: дистрибутивность дизъюнкции относительно конъюнкции и дистрибутивность конъюнкции относительно дизъюнкции. Первый тип схож с дистрибутивным законом алгебры, а второй — нет, поэтому его нужно доказывать.
Закон двойственности и инверсии (закон Моргана) — основоположником данного правила стал шотландский математик и логик де Морган. Он разработал правило, которое связывает логические операции конъюкцию (И) и дизъюнкцию (ИЛИ) с помощью отрицания.
Основные законы алгебры логики представлены в таблице:
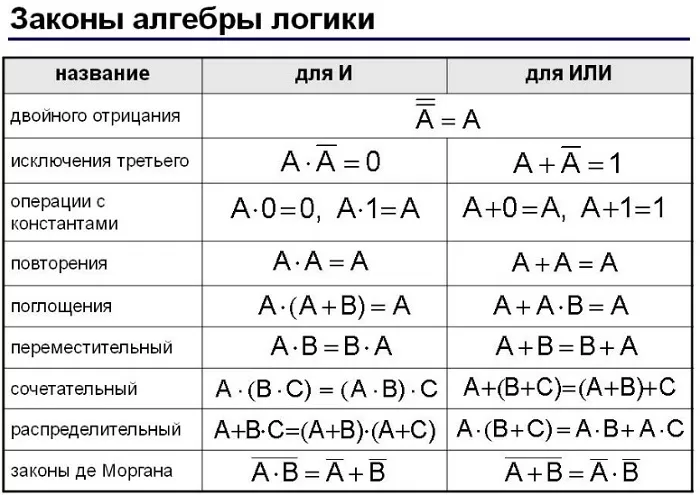
Унарные операции
Есть 4 унарные операции:
- Всегда правда
- Никогда не правда, унарная ложь
- Унарная идентичность
- Унарное отрицание
Выходное значение всегда истинно, независимо от входного значения p.
| п | Т |
|---|---|
| Т | Т |
| F | Т |
Логическая ложь
Выходное значение никогда не бывает истинным: то есть всегда ложно, независимо от входного значения p.
| п | F |
|---|---|
| Т | F |
| F | F |
Логическая идентичность
Логическая идентичность — это операция над одним логическим значением p, для которого выходное значение остается p.
Таблица истинности для оператора логической идентичности выглядит следующим образом:
| п | п |
|---|---|
| Т | Т |
| F | F |
Логическое отрицание
Логическое отрицание — это операция над одним логическим значением , обычно значением предложения , которая производит значение true, если его операнд ложен, и значение false, если его операнд истинен.
Таблица истинности для НЕ p (также записываемая как ¬p , Np , Fpq или ~ p ) выглядит следующим образом:
| п | ¬p |
|---|---|
| Т | F |
| F | Т |
Что такое таблица истинности?
Таблица истинности — это таблица, описывающая логическую функцию, а именно отражающую все значения функции при всех возможных значениях её аргументов. Таблица состоит из n+1 столбцов и 2 n строк, где n – число используемых переменных. В первых n столбцах записываются всевозможные значения аргументов (переменных) функции, а в n+1-ом столбце записываются значения функции, которые она принимает на данном наборе аргументов.
Довольно часто встречается вариант таблицы, в которой число столбцов равно n + число используемых логических операций. В такой таблице также первые n столбцов заполнены наборами аргументов, а оставшиеся столбцы заполняются значениями подфункций, входящих в запись функции, что позволяет упростить расчёт конечного значения функции за счёт уже промежуточных вычислений.
Аксиомы и законы
Построение таблиц в удобной форме позволяет определить, когда определённое действие или высказывание принимает верное значение, а в каком случае нет. В верхней строчке записывают логическую форму высказывания, а в столбцах — истинные значения. Некоторые комбинации высказываний всегда будут истинными или ложными, независимо от содержания. Поэтому и были сформулированы следующие законы:

- Торжества. Записывается в виде утверждения: А = А. В этом случае таблица будет состоять из двух комбинаций: ложной и правдивой. Бинарная логическая связка «Если А, то А» является материальной импликацией. Для такого варианта всегда можно сказать, что А есть А. Этот закон обозначает то, что нельзя подменять одно понятие другим, иначе возникнут логические ошибки.
- Противоречия. Согласно ему, утверждение, что А и НЕ-А, неверно: A & A = 0. Другими словами, если А истинное значение, то его отрицание не может быть ложным. То есть их перемножение будет всегда фальшивой операцией. Этот закон довольно часто применяется для упрощения сложных логических суждений.
- Третьего исключённого. Закон записывается в виде A v A = 1 и обозначает, что в один и тот же момент высказывание может быть только правдивым или ложным. То есть третьего не дано.
Эти три закона фундаментальны. Без их соблюдения сделать любое правильное утверждение невозможно.
Для решения логических задач с помощью таблиц истинности используют различные формулы, соответствующие разного вида операциям. Одно из них логическое умножение (конъюнкция). В этом случае считается, что функция истинная лишь тогда, когда оба выражения являются верными: F = A & B. Другое логическое сложение (дизъюнкция). Оно гласит, что если оба выражения ложны, то и логическая функция будет неверной.

Кроме того, используется закон:
- инверсии (отрицания) — если логическое высказывание истинно, то отрицание его будет ложным выражением;
- импликации (следования) — для всегда истинного сложного логического выражения ложь будет тогда, когда из верности следует отрицание;
- эквивалентности (равнозначности) — выражение будет истинным лишь тогда, когда оба высказывания имеют одинаковое значение.
Задача синтеза логических схем в базисах «И-НЕ» и «ИЛИ-НЕ»
Часто для сокращения числа микросхем используют элементы «И-НЕ» или/и «ИЛИ-НЕ».
Рассмтрим примеры, как построить схему, реализующую ту же функцию, что в предыдущем примере, но, сначала
в базисе «И-НЕ», а затем в базисе «ИЛИ-НЕ».
Пример 8. Построить в базисе «И-НЕ» логическую схему, реализующую
функцию алгебры логики .
Решение. Логическая функция должна быть приведена к виду, содержащему только операции
логического умножения (конъюнкции) и инвертирования (отрицания). Это делается при помощи двойного инвертирования
исходного выражения функции и применения :
Для построения логической схемы потребуются 8 схем «И-НЕ». Получаем следующую логическую схему:
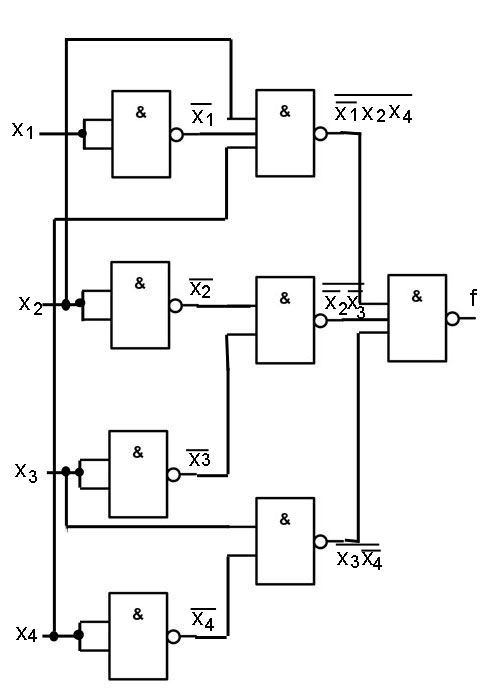
Пример 9. Построить в базисе «ИЛИ-НЕ» логическую схему, реализующую
функцию алгебры логики .
Пример задания
Пусть необходимо построить таблицу для логического выражения F = (A → B) * (A + B). Эта формула состоит из двух логических переменных A и B и нескольких операций. Начинают построение с определения строк. Используя формулу 2n+1 для рассматриваемого примера можно установить, что их число будет: x = 22 + 1 = 5.
Теперь следует определить число столбцов. Для этого используется формула, в которой учитывается количество переменных и операций. Последние можно просто посчитать, сложив количество разных знаков, используемых в записи формулы. Но правильней сначала расставить порядок операций, а затем посчитать. Согласно порядку действия над операциями их нумерацию можно представить в следующей очерёдности:
- Импликация в первой скобке.
- Инверсия во второй скобке переменной A.
- Отрицание во второй скобке неизвестной B.
- Сложение во втором члене.
- Конъюнкция.
В итоге получится, что столбцов будет: Y = 2 + 5 = 7. Теперь нужно построить таблицу 7Х5. В шапку первого и второго столбца вписывают переменные, а затем операции над ними. Затем в строках, соответствующих A и B нужно записать всё, что с ними может произойти. В итоге останется только правильно посчитать последний столбец.
Для этого нужно использовать законы. Необходимо выполнить логическое умножение значений в скобках. Первой и второй строчке будет соответствовать операция произведения один на один, что в ответе даст единицу. Третьей и четвёртой — ноль на один, что в итоге даст ноль. Последний столбец является главным для рассматриваемой логической функции. По нему можно узнать значение логической функции для любых форм переменных A и B.
Это довольно простая задача, содержащая всего две переменных. Но в реальности, например, в программировании, их может быть намного больше. Решать такие задания методом перебора проблематично. Поэтому при решении сложных примеров функцию вначале пытаются упростить.
Например, заданно выражение (x + y + z) * (x + y). По сути, оно записано в совершенно нормальной конъюнктивной форме. Но для приведения его к этому виду нужно, чтобы во втором выражении стояла z
Для того чтобы её добавить необходимо обратить внимание на то, что внутри скобок стоит логическое сложение. Поэтому дописав к нему ноль, результат не изменится
Добавить ноль через z можно, как ноль умножить на НЕ z. В итоге получится выражение (x + y + z) * (x + y + z + z), для которого, используя алгоритм составить таблицу уже не так и сложно.
Видеоинструкция к калькулятору
https://youtube.com/watch?v=0fbkpR41kKg
Используемые символы
В качестве переменных используются буквы латинского и русского алфавитов (большие и маленькие), а также цифры, написанные после буквы (индекс переменной). Таким образом, именами переменных будут: a , x , a1 , B , X , X1 , Y1 , A123 и так далее.
Для записи логических операций можно использовать как обычные символы клавиатуры ( * , + , ! , ^ , -> , = ), так и символы, устоявшиеся в литературе ( ∧ , ∨ , ¬ , ⊕ , → , ≡ ). Если на вашей клавиатуре отсутствует нужный символ операции, то используйте клавиатуру калькулятора (если она не видна, нажмите «Показать клавиатуру»), в которой доступны как все логические операции, так и набор наиболее часто используемых переменных.
Для смены порядка выполнения операций используются круглые скобки ().
Что умеет калькулятор
- Строить таблицу истинности по функции
- Строить таблицу истинности по двоичному вектору
- Строить совершенную конъюнктивную нормальную форму (СКНФ)
- Строить совершенную дизъюнктивную нормальную форму (СДНФ)
- Строить полином Жегалкина (методами Паскаля, треугольника, неопределённых коэффициентов)
- Определять принадлежность функции к каждому из пяти классов Поста
- Строить карту Карно
- Минимизировать ДНФ и КНФ
- Искать фиктивные переменные
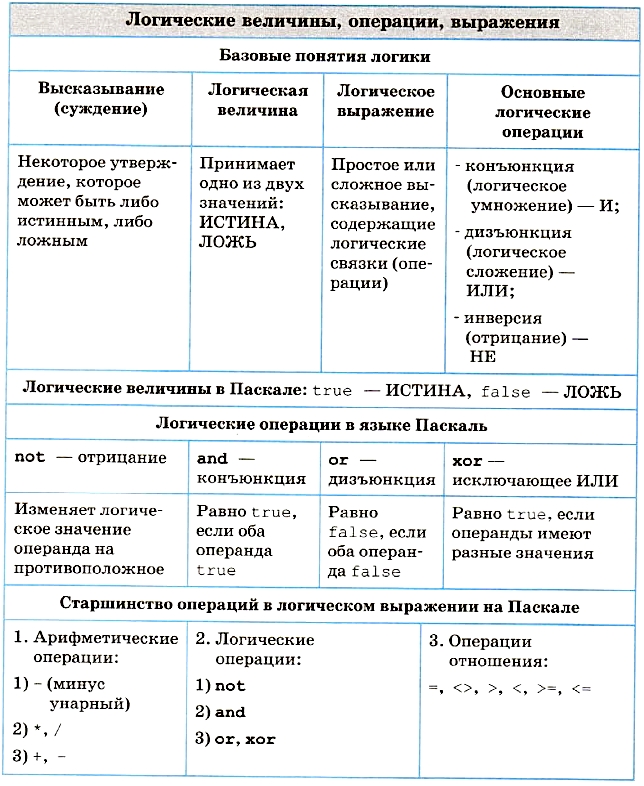
Логические выражения на Паскале
Уже говорилось о том, что в Паскале имеется логический тип данных.
Логические константы: true (истина), false (ложь).
Логические переменные: описываются с типом Boolean.
Операции отношения: осуществляют сравнение двух операндов и определяют, истинно или ложно соответствующее отношение между ними. Знаки операций отношения: = (равно), <> (не равно), > (больше), < (меньше), >= (больше или равно), <= (меньше или равно).
Логические операции: not — отрицание, and — логическое умножение (конъюнкция), or — логическое сложение (дизъюнкция), хог — исключающее ИЛИ. Таблица истинности для этих операций (Т — true; F — false):

Логическое выражение может состоять из логических констант и переменных, отношений, логических операций. Логическое выражение принимает значение true или false.
Например, логическая формула ¬Х & Y ∨ X & Z на Паскале запишется в виде следующего логического выражения:
где X, Y, Z — переменные типа boolean.
Логические операции располагаются в следующем порядке по убыванию старшинства (приоритета): 1) not, 2) and, 3) or, хог. Операции отношения имеют самый низкий приоритет. Поэтому если операндами логической операции являются отношения, то их следует заключать в круглые скобки. Например, математическому неравенству 1 < X < 50 соответствует следующее логическое выражение:
Логическая функция odd(x) принимает значение true, если значение целочисленного аргумента х является нечетным, иначе — false.
Для правильной записи сложного логического выражения (предиката) нужно учитывать относительные приоритеты арифметических, логических операций и операций отношений, поскольку все они могут присутствовать в логическом выражении. По убыванию приоритета операции располагаются в следующем порядке.
-
Арифметические операции:
-
Логические операции:
-
Операции отношения:
Еще раз обратите внимание, что в логическом выражении, соответствующем предикату из примера 3:
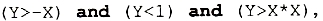
операции отношения заключены в скобки, поскольку они младше логических операций, а выполняться должны раньше.
Система основных понятий
Виды логических операций
В качестве наименьшей единицы измерения объёма данных принято считать бит. В него заносится одно из двух значений — ложь (0) или правда (1). Каждая ячейка, соответствующая биту, находится лишь в одном из этих состояний. Существуют определённые операции, используемые для действий с ячейками:
- AND (И) — применяется для сравнения двух бит. Результатом действия будет единица, но лишь в том случае, если значения двух ячеек одинаковое. При остальных вариантах итог будет иметь устойчивое нулевое состояние.
- OR (ИЛИ) — по сути, операция обратная AND. Результат становится нулевым, если содержимое двух сравниваемых бит одинаковое. В остальных случаях он равный единице.
- XOR (ИЛИ) — если значения, содержащиеся в двух сравниваемых битах противоположны, при выполнении логического действия результат будет равный единице. Во всех остальных случаях он будет равняться нулю.
- NOT (НЕ) — действие, используемое для одного бита. Если первоначально ячейка находилась в нулевом состоянии, то после выполнения над ней операции она станет равной единице и наоборот. Фактические это логическая инверсия.
Эти операции являются основными элементами при составлении таблиц истинности и получения возможного результата. На основании их построена алгебра Буля. Некоторые элементы получаются путём объединения нескольких операций. Так, существует состояние: NAND (И-НЕ) и NOR (ИЛИ-НЕ). Первый элемент является инверсией операции «И», а второй — «ИЛИ». На основании рассмотренных операторов строится работа всех цифровых интегральных схем.
Как задать логическую функцию
Есть множество способов задать булеву функцию:
- таблица истинности
- характеристические множества
- вектор значений
- матрица Грея
- формулы
Рассмотрим некоторые из них:
Чтобы задать функцию через вектор значений необходимо записать вектор из 2 n нулей и единиц, где n – число аргументов, от которых зависит функция. Например, функцию двух аргументов можно задать так: 0001 (операция И), 0111 (операция ИЛИ).
Чтобы задать функцию в виде формулы, необходимо записать математическое выражение, состоящее из аргументов функции и логических операций. Например, можно задать такую функцию: a∧b ∨ b∧c ∨ a∧c
Алгебраические преобразования логических выражений
Любое логическое выражение, как и его переменные (утверждения), принимают два значения: ложь или истина. Ложь обозначается нулём, а истина — единицей. Разобравшись с областью определения и областью допустимых значений, мы можем рассмотреть действия алгебры логики.
Отрицание
Отрицание и инверсия — самое простое логическое преобразование. Ему соответствует частица «не.» Это преобразование просто меняет утверждение на противоположное. Соответственно, значение утверждения тоже меняется на противоположное. Если утверждение А истинно, то «не А» — ложно. Например, утверждение «прямой угол — это угол, равный девяносто градусов» — истина. Тогда его отрицание «прямой угол не равен девяноста градусам» — ложь.
Таблица истинности для отрицания будет такова:
| А | не А |
| Л | И |
| И | Л |
Конъюнкция
Конъюнкция аналогична умножению и соответствует союзу «и». Такое выражение будет верно, только если верны все утверждения, объединённые конъюнкцией. То есть, утверждение «А и Б» будет истинным, только если А — истина и Б — истина. Во всех остальных случаях выражение «А и Б» ложно. Например, высказывание «Земля круглая и плоская» будет ложно, так как первая часть истина, а вторая — ложь.
Таблица истинности конъюнкции
| А | Б | А и Б |
| Л | Л | Л |
| Л | И | Л |
| И | Л | Л |
| И | И | И |
Дизъюнкция
Эта операция может быть обычной или строгой, их результаты будут различаться.
Обычная дизъюнкция или логическое сложение соответствует союзу «или». Она будет истинной если хотя бы одно из утверждений, входящих в неё — истина. Например, выражение «Земля круглая или стоит на трёх китах» будет истинным, так как первое утверждение — истинно, хоть второе и ложно.В таблице это будет выглядеть так:
| А | Б | А или Б |
| Л | Л | Л |
| Л | И | И |
| И | Л | И |
| И | И | И |
Строгую дизъюнкцию или сложение по модулю также называют «исключающим или». Эта операция может принимать вид грамматической конструкции «одно из двух: либо …, либо …». Здесь значение логического выражения будет ложным, если все утверждения, входящие в него, имеют одинаковую истинность. То есть, оба утверждения либо вместе истинны, либо вместе ложны.
Таблица значений исключающего или
| А | Б | либо А, либо Б |
| Л | Л | Л |
| Л | И | И |
| И | Л | И |
| И | И | Л |
Импликация и эквивалентность
Импликация представляет собой следствие и грамматически может быть выражена как «из А следует Б». Здесь утверждение А будет называться предпосылкой, а Б — следствием. Импликация может быть ложной, только в одном случае: если предпосылка истинна, а следствие ложно. То есть, ложь не может следовать из истины. Во всех остальных случаях импликация истинна. Варианты, когда оба утверждения имеют одинаковую истинность, вопросов не вызывают. Но почему верное следствие из неверной предпосылки — истина? Дело в том, что из ложной предпосылки может следовать что угодно. Это и отличает импликацию от эквивалентности.
В математике (и других доказательных дисциплинах) импликация используется для указания необходимого условия. Например, утверждение А — «точка О — экстремум непрерывной функции», утверждение Б — «производная непрерывной функции в точке О обращается в ноль». Если О, действительно, точка экстремума непрерывной функции, то производная в этой точке будет, и вправду, равна нулю. Если же О не является точкой экстремума, то производная в этой точке может быть нулевой, а может не быть. То есть Б необходимо для А, но не достаточно.
Таблица истинности для импликации выглядит следующим образом:
| А | Б | из А следует Б |
| Л | Л | И |
| Л | И | И |
| И | Л | Л |
| И | И | И |
Логическая операция эквивалентность, по сути, является взаимной импликацией. «А эквивалентно Б» означает, что «из А следует Б» и «из Б следует А» одновременно. Эквивалентность верна, когда оба утверждения либо одновременно верные, либо одновременно неверные.
| А | Б | А эквивалентно Б |
| Л | Л | И |
| Л | И | Л |
| И | Л | Л |
| И | И | И |
В математике эквивалентность используется для определения необходимого и достаточного условия. Например, утверждение А — «Точка О является точкой экстремума непрерывной функции», утверждение Б — «В точке О производная функции обращается в ноль и меняет знак». Эти два утверждения эквивалентны. Б содержит необходимое и достаточное условие для А
Обратите внимание, что в данном примере утверждений Б на самом деле является конъюнкцией двух других: «производная в точке О обращается в ноль» и «производная в точке О меняет знак»
Прочие логические функции
Выше были рассмотрены основные логические операции, которые часто используются. Есть и другие функции, которые используются:
- Штрих Шеффера или несовместимость представляет собой отрицание конъюнкции А и Б
- Стрелка Пирса представляет сбой отрицание дизъюнкции.
Приложения
Таблицы истинности могут использоваться для доказательства многих других логических эквивалентностей . Например, рассмотрим следующую таблицу истинности:
| п{\ displaystyle p} | q{\ displaystyle q} | ¬п{\ displaystyle \ lnot p} | ¬п∨q{\ Displaystyle \ lnot p \ lor q} | п⇒q{\ displaystyle p \ Rightarrow q} |
|---|---|---|---|---|
| Т | Т | F | Т | Т |
| Т | F | F | F | F |
| F | Т | Т | Т | Т |
| F | F | Т | Т | Т |
Это свидетельствует о том , что является логическим эквивалентом к .
п⇒q{\ displaystyle p \ Rightarrow q}¬п∨q{\ Displaystyle \ lnot p \ lor q}
Таблица истинности для наиболее часто используемых логических операторов
Вот таблица истинности, которая дает определения 7 наиболее часто используемых из :
| п | Q | п∧Q{\ displaystyle P \ land Q} | п∨Q{\ Displaystyle P \ lor Q} | п ∨_ Q{\ Displaystyle P \ {\ underline {\ lor}} \ Q} | п ∧_ Q{\ Displaystyle P \ {\ underline {\ land}} \ Q} | п⇒Q{\ Displaystyle P \ Rightarrow Q} | п⇐Q{\ Displaystyle P \ Leftarrow Q} | п⇔Q{\ displaystyle P \ Leftrightarrow Q} |
|---|---|---|---|---|---|---|---|---|
| Т | Т | Т | Т | F | Т | Т | Т | Т |
| Т | F | F | Т | Т | F | F | Т | F |
| F | Т | F | Т | Т | F | Т | F | F |
| F | F | F | F | F | Т | Т | Т | Т |
| п | Q | п∧Q{\ displaystyle P \ land Q} | п∨Q{\ Displaystyle P \ lor Q} | п ∨_ Q{\ Displaystyle P \ {\ underline {\ lor}} \ Q} | п ∧_ Q{\ Displaystyle P \ {\ underline {\ land}} \ Q} | п⇒Q{\ Displaystyle P \ Rightarrow Q} | п⇐Q{\ Displaystyle P \ Leftarrow Q} | п⇔Q{\ displaystyle P \ Leftrightarrow Q} |
| И (союз) | ИЛИ (дизъюнкция) | XOR (исключающее или) |
XNOR ( исключая ни) |
условное «если-то» | условное «тогда-если» | двусмысленное выражение «если и только если» | ||
|
куда Т значит правда и F означает ложь |
Сжатые таблицы истинности для бинарных операторов
Для бинарных операторов также используется сжатая форма таблицы истинности, где заголовки строк и заголовки столбцов определяют операнды, а ячейки таблицы определяют результат. Например, в булевой логике используется эта сжатая запись таблицы истинности:
[править] Второстепенные операции
Сильная дизъюнкция
Исключающая дизъюнкция, выражение «XOR», обозначается символами «⊻» или «⊕».
Таблица истинности для пары операндов — 0110. Возвращает 1 только тогда, когда только один из них равен 1, а второй равен 0.
Может быть определена через основные операции: (A ⊻ B) = ((A ∧ ¬ B) ⋁ (¬ A ∧ B)).
Эквивалентность
Тождество, равенство, выражение «EQ», обозначается символами «», «⇔» или «≡».
Таблица истинности для пары операндов — 1001. Возвращает 1 только тогда, когда оба операнда равны одновременно 0 или 1.
Может быть определена через основные операции: (A ⇔ B) = ((A ∧ B) ⋁ (¬ A ∧ ¬ B)).
Выражение «НЕ-ИЛИ»
Иначе стрелка Пирса, выражение «NOR», обозначается символом «↓».
Таблица истинности для пары операндов — 0001. Возвращает 1 только тогда, когда оба операнда одновременно равны 0.
Может быть определена через основные операции: (A ↓ B) = (¬ A ∧ ¬ B)
Также через NOR могут быть определены основные логические функции.
Импликация
Выражает зависимость причины и следствия, обозначается символами «⇒», «→» или «⊃».
Таблица истинности для пары операндов — 1011. То есть возвращает ложь только тогда, когда первый операнд равен 1, а второй — 0.
Может быть определена через основные операции: (A → B) = (¬ A ⋁ B).
Штрих Шеффера
Записывается обычно как «|»
Таблица истинности — 1110. Возвращает 0 только тогда, когда оба операнда равны 1.
Можно определить через основные операции как ¬(A ∧ B)
Операция И — логическое умножение (конъюнкция)
Логическая операция И выполняет функцию пересечения двух высказываний (аргументов), в качестве которых может быть и простое, и сложное логическое выражение. Результатом операции И является выражение, которое будет истинным тогда и только тогда, когда истинны оба исходных выражения.
Применяемые обозначения: А и В, А ? В, A & B, A and B.
Результат операции И определяется следующей таблицей истинности:
| A | B | А и B |
| 1 | ||
| 1 | ||
| 1 | 1 | 1 |
Результат операции И истинен тогда и только тогда, когда истинны одновременно высказывания А и В, и ложен во всех остальных случаях.
Приведем примеры логического умножения.
1. Рассмотрим высказывание «Умение и настойчивость приводит к достижению цели». Достижение цели возможно только при одновременной истинности двух предпосылок — умения И настойчивости.
Логическую операцию И можно сравнить с последовательным соединением лампочек в гирлянде. При наличии хотя бы одной неработающей лампочки электрическая цепь оказывается разомкнутой, то есть гирлянда не работает. Ток протекает только при одном условии — все составляющие цепи должны быть исправны.
Операция «ЕСЛИ-ТО» — логическое следование (импликация)
Эта операция связывает два простых логических выражения, из которых первое является условием, а второе — следствием из этого условия.
Применяемые обозначения:
если А, то В; А влечет В; if A then В; А? В.
Таблица истинности:
| A | B | А ? B |
| 1 | ||
| 1 | 1 | |
| 1 | ||
| 1 | 1 | 1 |
Результат операции следования (импликации) ложен только тогда, когда предпосылка А истинна, а заключение В (следствие) ложно.
Приведем примеры операции следования.
1. Рассмотрим высказывание «Если идет дождь, то на улице сыро». Здесь исходные высказывания «Идет дождь» и «На улице сыро». Если не идет дождь и не сыро на улице, результат операции следования — истина. На улице может быть сыро и без дождя, например, когда прошла поливочная машина или дождь прошел накануне. Результат операции ложен только тогда, когда дождь идет, а на улице не сыро.
2. Рассмотрим два высказывания: А {х делится на 9}, В {х делится на 3}. Операция А ? В означает следующее: «Если число делится на 9, то оно делится и на 3». Рассмотрим возможные варианты:
? А — ложно, В — ложно (1-я строка таблицы истинности). Можно найти такие числа, для которых истиной является высказывание «если А — ложно, то и В — ложно». Например, х = 4, 17, 22.
? А — ложно, В — истинно (2-я строка таблицы истинности). Можно найти такие числа, для которых истиной является высказывание «если А — ложно, то В — истинно». Например, х = б, 12, 21.
? А — истинно, В — ложно (3-я строка таблицы истинности). Невозможно найти такие числа, которые делились бы на 9, но не делились на 3. Истинная предпосылка не может приводить к ложному результату импликации.
? А — истинно, В — истинно (4-я строка таблицы истинности). Можно найти такие числа, для которых истиной является высказывание «если А — истинно, то и В — истинно». Например, х = 9, 18, 27.
Практика
Основных вариантов решения два: логические рассуждения, либо построение таблицы истинности. Иногда проще решать первым методом, иногда вторым.
Первый метод. Логические рассуждения.
Пример:
Логическая функция F задаётся выражением y ∧ (x → z) ∧ ¬w. Во фрагменте таблицы истинности приведены все строки, при которых значение функции F истинно.Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
Решение:
Итоговая функция всегда истинна для нашей таблицы (единички в значениях F). Заметим, что в последнюю очередь выполняются две конъюнкции, значение которых будет = 1 только тогда, когда значение каждого выражение равно 1.
Вывод:y = 1(x → z) = 1¬w = 1,а значит w = 0
y всегда 1, такой столбик лишь один: y — переменная 4w всегда 0, такой столбик лишь один: w — переменная 2
Для x и z остаётся переменная 1 и переменная 3. Осталось определится с порядком.(x → z) = 1, значит не может быть набора, когда x = 1, а z = 0. Во второй строчке перем1 = 1, а перем3 = 0. Следовательно, z — переменная 1, x — переменная 3.
z — переменная 1w — переменная 2x — переменная 3y — переменная 4Ответ: zwxy
Второй метод. Таблица истинности
Пример:
Логическая функция F задаётся выражением (y → w) ∨ (¬x ∧ z). Во фрагменте таблицы истинности приведены все строки, при которых значение функции F ложно. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
Решение:
Итоговая функция всегда равна нулю. Между скобками дизъюнкция, значит обе скобки должны быть ложными. Рассмотрим каждую скобку отдельно:
y → w = 0
¬x ∧ z = 0
Объединяем все переменные в одну таблицу:
Построение электронных схем, реализующих логические операции
Если рассмотреть электросхемы с точки зрения логики, особенно компьютерные, то их также можно описать при помощи «1» и «0» – электричество идет или не идет по проводам.
Попробуем нарисовать логические элементы схемы питания лампочки для нескольких простых операций.
Электросхема с конъюнктором

Рассмотрим все варианты:
- Все контакты включены, тогда источник света горит.
- Первый контакт в положении «выключено» – свет не горит.
- Второй контакт выключен – лампа не светит.
- Все контакты отключены – свет не горит.
Заключение – эта электрическая цепь реализует операцию «И».
Дизъюнктор, схема электропитания
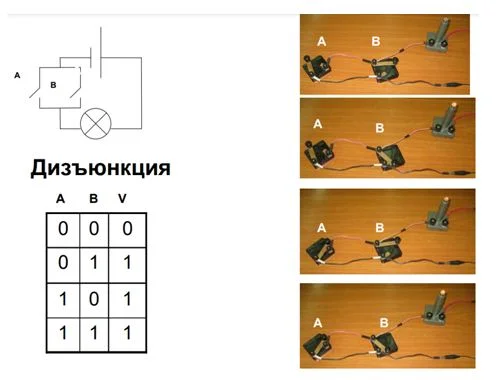
Рассмотрим этот вид электрической цепочки:
- Все контакты включены – лампа горит.
- Первый контакт включен, второй выключен – свет горит.
- Обратная ситуация – выключен первый, включен второй – лампа светится.
- Все контакты выключены – света нет.
Заключение – такой вид электросхем соответствует логической операции «ИЛИ».
Инвертор в электросхемах
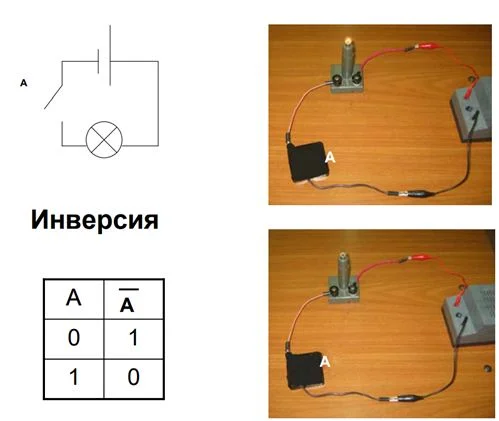
В этой схеме переключатель не ручной, а автоматический. Здесь процесс обратный – когда ток не идет, контакты замыкаются, горит свет. Если же в сеть подается электричество, пластинка размыкается вследствие электромагнитной индукции, и сеть разъединяется – света нет.
Заключение: схема соответствует логической операции «НЕ».
Умение читать и решать логические операции, строить соответствующие электросхемы, позволяет создавать иерархически более сложные конструкции, которые используются для реализации процессов в современных ПК.
[править] См. также
- Логическая функция
- Вычисление
- Булева логика
| Формальная |
Логические операции с понятиями
Изменение содержания понятия: отрицание • ограничение • обобщение • делениеИзменение объёма понятия: сложение • умножение • вычитаниеТипы: Многозначная логика • Бинарная логика |
|---|---|
| Математическая (теоретическая, символическая) |
Логические связки (операции) над высказываниями
Высказывание — построение над множеством {B, \lnot, \land, \lor, 0, 1} |
| См. также | импликация (\to) • Круги Эйлера/Диаграмма Венна • Полилогизм • Теория множеств |
Алгебра логики и решение задач
Несмотря на то, что логика, как наука о размышлении, существовала еще 5 в. До н.э., теперь это важная часть многих наук, а не только философии и риторики. Также логика существует, как отдельная наука уже более 200 лет.
Инструменты алгебры логики позволяют переводить словесные высказывания в сухие, объективные выражения, а с их помощью выполнять различные логические операции.Появился этот раздел математики 200 лет назад.
Стоит остановиться на базовых понятиях алгебры логики:
- константы (0,1);
- переменные;
- формула;
- знаки операций;
- скобки.
Логическая переменная – обозначение логического выражения, которое может быть true (t, правда, истина, да, 1) – false (f, ложь, нет, 0).
Формула– символьный способ выражения операции между переменными при помощи специальных знаков и скобок ().
Логическое высказывание – утверждение, в котором говорится только правда или только ложь.
Образец таких предложений: «Луна – вертится вокруг Марса» – ложно, а «После зимы всегда приходит весна» – истинно.
Частицы «не», «или», если», «и» и другие, которые являются связующими элементами в обычной речи, позволяют создавать элементарные логические выражения.
Элементарные высказывания – те, к которым нельзя применить понятие истинности или ложности. Их обозначают различными символами (латинские буквы, цифры), знаками. Ими занимаются те сферы, к которым они относятся. Они входят в состав высказываний логики.
Из одних высказываний можно образовывать другие, в результате получая составные высказывания. И от того, являются исходные элементы составного конечного высказывания правдивыми или неправдивыми, а также какие логические связки использовались, будет правдой или ложью все высказывание в целом.
Чтобы образовать такое составное предложение в обычной жизни, используют связки И, ИЛИ, НЕ. А научный подход заменил их на конъюнкцию, дизъюнкцию, инверсию и более сложные операции. Все эти процессы выражают словесно, таблично (таблицы истинности) или графически (диаграммы Эйлера-Венна).
Простые выражения содержат лишь одно выражение (правдивое или нет), и не содержит никаких логических операций.
Сложные могут содержать от 2 и больше аргументов (простых выражений), которые между собой связаны логическими операциями.
Еще используют понятие «предикат» – содержит любое количество переменных без перечисления всех составляющих данных. Это предикат простых, отрицательных P(x)=(x<0) чисел.
Чтобы исключить лишнюю информацию, оставив только логические связи, используют таблицы истинности, наглядно демонстрирующие, правдиво или неправдиво конечное предложение, если учесть все значения входящих в его состав простейших частей.
Такая форма оформления и решения задач используется в построении электросхем, для решения различных логических задач, в булевой алгебре, программировании.