Соединение резисторов последовательное, параллельное, смешанное. пример расчета

Последовательное соединение

Последовательным называется соединение двух и более резисторов, при котором конец первого элемента соединяется с началом второго и так далее. В результате получается последовательная цепочка, где по всем ее составляющим проходит одинаковый ток. В качестве примера можно взять последовательную цепь, состоящую из трех резисторов R1, R2 и R3. Сопротивление в источнике тока принимается с нулевым значением. В соответствии со вторым законом Кирхгофа получается следующая формула: E = IR1 + IR2 + IR3 = I(R1 + R2 + R3) = IRэк.
В этой формуле значение эквивалентного сопротивления последовательной цепи составит сумму сопротивлений всех резисторов, имеющихся в данной цепи: Rэк = R1 + R2 + R3. По закону Ома напряжение при последовательном соединении на отдельных участках будет иметь следующее значение, поскольку E = U: U1=IR1; U2 = IR2, U3 = IRз, то есть U = U1 + U2 +U3. Данные формулы показывают, что в резисторах, последовательно соединенных между собой, напряжения распределяются пропорционально их сопротивлениям. То есть, чем выше сопротивление любого из резисторов, тем больше напряжение, приложенное к нему. В виде формулы — это утверждение будет выглядеть следующим образом: U1 : U2 : U3 = R1 : R2 : R3.

При последовательном соединении сопротивление R1 нескольких резисторов в количестве n, будет одинаковым. Следовательно, значение эквивалентного сопротивления цепи будет в n раз превышать сопротивление каждого из них: Rэк = nR1. Следовательно напряжение на каждом отдельном резисторе будет в n раз меньше, чем общее напряжение цепи: U1 = U/n.

Таким образом, изменение сопротивления любого из резисторов при последовательном соединении, приводит к изменению напряжения на других резисторах, находящихся с ним в одной цепи. Поэтому, если электрическая цепь обрывается или выключается в одной из нагрузок, в других нагрузках также прекращается течение тока. Из-за этого последовательное соединение в электрических схемах используется довольно редко.

Зависимость сопротивления

Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:

Температура окружающей среды и материала.
Электрические величины.
Геометрические свойства вещества.
Тип материала, из которого изготовлен проводник (полупроводник).

https://youtube.com/watch?v=lVYhHuFjdio

Электрические величины

Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.

Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.

Тип и геометрические параметры

Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.

Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:

Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
Визуально определить форму материала.
Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.

В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.

https://youtube.com/watch?v=UR_SlbmYh0c

Температурные показатели

Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.

В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * . Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.

Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a<0. Для получения формулы, определяющей все зависимости, необходимо подставить все соотношения в общую формулу зависимости R от типа материала, температуры, длины и сечения: R = p0 * * L / S. Формулы используются только для расчетов и изготовления резисторов. Для быстрого измерения величины сопротивления применяется омметр.

Ток в цепи параллельно соединенных резисторов

В ходе рассмотрения соответствующих участков разветвленных схем необходимо помнить о равенстве токов на входе и выходе из каждого узла, а также до и после группы из параллельных резисторов. Это правило поможет проверить правильность расчетов. Если отмеченное соответствие не соблюдено, устраняют ошибку вычислений.

Сила тока при параллельном соединении

С применением рассмотренных выше исходных данных для двух сложных схем можно сделать расчет для каждой отдельной ветки.

Пример 1:

общий ток в цепи составляет 0,8 А;
распределение напряжений на отдельных участках несложно определить по рассчитанным эквивалентным сопротивлениям: U12 = I * Rэкв1 = 0,8 * (2*4)/ (2+4) = 0,8 * 1,3 = 1,04 V;
по стандартному алгоритму вычисляют значения токов: I1 = U12/R1 = 0,52 А, I2 = U12/R2 = 0,26 А;
суммированием проверяют корректность вычислений: I = I1 + I2 = 0,52 + 0,26 ≈ 0,8 А.

Пример 2 (смешанный способ соединения резисторов):

ток в этом варианте – 1,2 А;
напряжение на участке с группой параллельных резисторов составляет Uав = I * Rэкв(12345) = 1,2*2,5 =3V;
по аналогии с предыдущим примером несложно вычислить ток в каждой отдельной ветке: I12 = Uав/(R1 + R2) = 3/ (15 + 5) = 0,15 А;
I3 = Uав/ R3 = 3/ 5 = 0,6 А;
I4 = Uав/ R4 = 3/ 10 = 0,3 А;
I5 = Uав/ R5 = 3/20 = 0,15 А;
по правилу равенства токов на входе и выходе из узла проверяют правильность сделанных расчетов: I = I12 + I3 + I4 + I5 = 0,15 + 0,6 + 0,3 + 0,15 = 1,2 А.

Мощность при параллельном соединении

Для правильного выбора резистивных компонентов электрических цепей обязательно следует учитывать мощность рассеивания. Этот параметр (Р) рассчитывают по классической формуле P = U (напряжение на выводах, В) * I (сила тока в цепи, А). Он косвенно определяет энергию, которая расходуется на выделение тепла. Также применяют пропорции:

P = I2 *R = U2/ R.

К сведению. Конструкция каждого элемента рассчитана на определенный рабочий температурный диапазон. Превышение порога способно разрушить деталь, место пайки, соседние компоненты. Следует не забывать об одновременном существенном изменении сопротивления, которое способно нарушить функциональное состояние электрической схемы.

Для расчета выбирают подходящую формулу с учетом известных исходных параметров (данные из примера 2 в предыдущем разделе):

ток – 1,2 А;
на сопротивлении R6=7,5 Ом мощность рассеивания составит: P6 = I2 *R = 1,44 * 7,5 = 10,8 Вт;
найти такой резистор сложно, так как в стандартном ряду предлагаются номиналы от 0,05 до 5Вт;
в другой цепи (R5=20 Ом) расчетный ток составит 0,15 А, поэтому P5= 0,0225 * 20 = 0,45 Вт;
в этом случае можно выбрать изделие с подходящей мощностью рассеивания в стандартной номенклатуре 0,5 Вт (специалисты рекомендуют делать 1,52 кратный запас, поэтому лучше использовать резистор на 1 Вт).

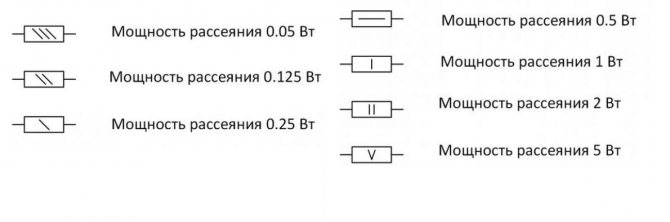
Стандартные обозначения на электрических схемах и типовые номиналы по мощности

К сведению. При выборе резисторов следует учитывать класс изделия по точности электрического сопротивления. В серийных деталях допустимы отклонения 5-20%.

Как найти сопротивление при параллельном соединении

Для расчета этого параметра применяют формулы:

1/G;
U/I;
U2/P;
P/I2.

Выбирают подходящий вариант (комбинацию) с учетом имеющихся исходных данных. Следует помнить о едином напряжении на входе и выходе и разных токах в отдельных ветках. Технология вычислений рассмотрена в предыдущих разделах.

Основные законы

Проектирование электрических цепей предполагает наличие хороших знаний основных закономерностей последовательного и параллельного подключения нагрузки. Это касается не только закона Ома, но и постулатов Кирхгофа. Эти физики внесли большой вклад в развитие электротехники. Для более простого восприятия основных законов все формулы стоит рассматривать в следующей последовательности:

при последовательном соединении через каждый участок цепи протекает ток одинаковой силы;
общее сопротивление схемы при последовательном подключении равно сумме сопротивления всех проводников;
напряжение в электросети при параллельном подключении одинаково для каждого участка;

Для последовательного соединения нагрузок применим второй закон Кирхгофа. Согласно ему, сумма ЭДС в замкнутом электрическом контуре равна сумме падений напряжений на каждой нагрузке. В результате общее сопротивление можно определить с помощью следующей формулы: Ro = R1 + R2.

Также можно рассчитать и индуктивность при различных видах соединения катушек. В случае с последовательным все довольно просто, достаточно использовать следующую формулу: Lo = L1 + L2. По сути, вместо двух элементов можно установить один с соответствующим показателем индуктивности.

При параллельном подсоединении катушек ситуация усложняется, так как возможны три варианта:

магнитные поля катушек не пересекаются: Lo = L1 * L2 / L1 + L2;
катушки подсоединены в одном направлении и их поля пересекаются: Lo = L1 * L2-М2 / L1 + L2 — 2 М;
пересечение полей наблюдается при встречном подсоединении: Lo = L1 * L2-М2 / L1 + L2 + 2 М.

Объединение резистивных радиокомпонентов

Для получения необходимого номинала сопротивления применяются два типа соединения резисторов: параллельное и последовательное. Если их соединить параллельно, то нужно два вывода одного резистора подключить к двум выводам другого. Если соединение является последовательным, то один вывод резистора соединяется с одним выводом другого резистора. Соединения используются для получения необходимых номиналов сопротивлений, а также для увеличения рассеивания мощности тока, протекающего по цепи.

Параллельное соединение

При параллельном подключении значение напряжения на всех резисторах одинаковое, а сила тока — обратно пропорциональна их общему сопротивлению. В интернете web-разработчики создали для расчета величины общего сопротивления параллельного соединения резисторов онлайн-калькулятор.

Рассчитывается общее сопротивление при параллельном соединении по формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + …+ (1 / Rn). Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ. Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).

При ремонте или проектировании схемы устройства возникает задача объединения нескольких резистивных элементов для получения конкретной величины сопротивления. Например, значение Rобщ для определенной цепочки элементов равно 8 Ом, которое получено при расчетах. Перед радиолюбителем стоит задача, какие нужно подобрать номиналы для получения нужного значения (в стандартном ряду резисторов отсутствует радиокомпонент с номиналом в 8 Ом, а только 7,5 и 8,2). В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:

Номинал резистора в 16 Ом подойдет.
Подставить в формулу: R = (16 * 16) / (16 + 16) = 256 / 32 = 8 (Ом).

Вам это будет интересно Устройство и принцип действия амперметра для измерения тока

В некоторых случаях следует потратить больше времени на подбор необходимых номиналов. Можно применять не только два, но и три элемента. Сила тока вычисляется с использованием первого закона Кирхгофа. Формулировка закона следующая: общее значение тока, входящего и протекающего по цепи, равен выходному его значению. Величина силы тока для цепи, состоящей из двух резисторов (параллельное соединение) рассчитывается по такому алгоритму:

Ток, протекающий через R1 и R2: I1 = U / R1 и I2 = U / R2 соответственно.
Общий ток — сложение токов на резисторах: Iобщ = I1 + I2.

Например, если цепь состоит из 2 резисторов, соединенных параллельно, с номиналами в 16 и 7,5 Ом. Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).

Последовательное подключение

Последовательное включение резисторов также применяется в радиотехнике. Методы нахождения общего сопротивления, напряжения и тока отличаются от параллельного подключения. Основные правила соединения следующие:

Ток не изменяется на участке цепи.
Общее напряжение равно сумме падений напряжений на каждом резисторе.
Rобщ = R1 + R2 + … + Rn.

Пример задачи следующий: цепочка, состоящая из 2 резисторов (16 и 7,5 Ом), питается от источника напряжением 12 В и током в 0,5 А. Необходимо рассчитать электрические параметры для каждого элемента. Порядок расчета следующий:

I = I1 = I2 = 0,5 (А).
Rобщ = R1 + R2 = 16 + 7,5 = 23,5 (Ом).
Падения напряжения: U1 = I * R1 = 0,5 * 16 = 8 (В) и U2 = I * R2 = 0,5 * 7,5 = 3,75 (В).

Не всегда выполняется равенство напряжений (12 В не равно 8 + 3,75 = 11,75 В), поскольку при этом расчете не учитывается сопротивление соединительных проводов. Если схема является сложной, и в ней встречается два типа соединений, то нужно выполнять расчеты по участкам. В первую очередь, рассчитать для параллельного соединения, а затем для последовательного.

Параллельное соединение большого числа резисторов

Если параллельно соединить N резисторов — R1,R2… RN, то, пользуясь вышеприведенными формулами и соображениями, можно получить выражение для обратной величины общего сопротивления такой цепи:

$$ {1over R}={ 1 over R1}+ {1 over R2}+…+{1 over RN}$$.

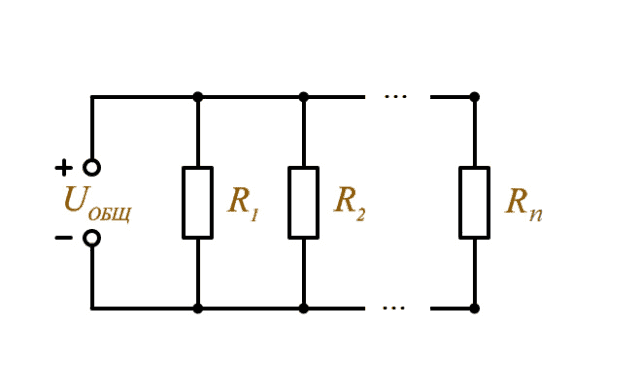
Рис. 3. Схема параллельного соединения нескольких резисторов R1,R2… Rn:.

Рассмотрим частный случай, когда все N резисторов одинаковы и равны R0. Тогда общее сопротивление цепи равно:

$$ R={R0 over N}$$

Таким образом, можно сформулировать общее правило: при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлений параллельно включенных проводников.

Российские химики разработали полимерные катоды для сверхбыстрых аккумуляторов

Спрос на литий-ионные аккумуляторы постоянно растет, но сырье для их изготовления ограничено, и ученые ищут другие варианты этой технологии. Российские исследователи из Сколтеха, РХТУ и ИПХФ синтезировали новые катодные материалы на основе полимеров и испытали их в литиевых двухионных батареях. Они показали, что такие катоды могут выдерживать до 25,000 циклов работы, а также заряжаться за несколько секунд, что превосходит возможности современных литий-ионных аккумуляторов. Также с применением новых катодов могут быть созданы калиевые двухионные аккумуляторы, не использующие дорогостоящий литий. Результаты работы опубликованы в журнале Energy Technology.

Что такое резистор и для чего он нужен

Резистор — это радиоэлемент, который увеличивает сопротивление цепи. Ставят его обычно для того, чтобы понизить/ограничить напряжение или ток. Есть сопротивления постоянные и переменные.

Например, светодиоды требуют небольшого тока, иначе перегревается и быстро выходит из строя. Чтобы ограничить ток, перед светодиодом поставьте сопротивление. Ток в цепи станет меньше.

Для чего нужны резисторы: для подстройки параметров питания

Постоянные сопротивления — это те, которые не меняют своего номинала в процессе работы. Если это и происходит, то считается выходом из строя.

Так выглядят переменные и постоянные резисторы

Переменные резисторы, наоборот, отличаются тем, что их сопротивление можно изменять. Они имеют бегунок или поворотную ручку, при помощи которых и изменяется номинал. На основе таких устройств делают регуляторы. Например, регулятор громкости, накала греющего элемента и т.д.

Смешанные электрические цепи

Определение 1

Смешанным соединением элементов называют всевозможные сочетания последовательной и параллельной разновидностей соединений. В такой цепи возможно различное количество узлов и ветвей.

Смешанным считают такое соединение, при котором в цепи существуют группы сопротивлений, включенных параллельно и последовательно.

Если все сопротивления в этой схеме принимаются за одинаковые, то есть это выглядит таким образом: $R_1 = R_2 = R_3 = R_4 = R_5 = R$, а сопротивления $R_4$ и $R_5$ будут включенными параллельно, то сопротивление участка цепи $cd$ определяется такой формулой:

$R_{cd} = \frac{R_4 R_5}{R_4+R_5} = \frac{R}{2}$

При последовательном соединении сопротивлений $R_3$ и $R_{cd}$ сопротивление участка цепи $ad$ определяется формулой:

$R_{ad} = R_3 + R_cd = R+\frac{R}{2}$

Смешанное соединение и сложные электрические цепи

Частым явлением в электрических цепях считается соединение смешанного типа (то есть комбинирование параллельного и последовательного соединений).

Ничего непонятно?

Попробуй обратиться за помощью к преподавателям

Если, например, взять 3 прибора, то возможными будут два варианта смешанного соединения. В первом случае мы наблюдаем соединение двух приборов параллельным образом при последовательном подключении к ним третьего.

https://youtube.com/watch?v=yPiOnYWXuDQ

При условии большего количества приборов, схемы смешанного соединения будут более сложными. Иногда встречаются также усложненные цепи, содержащие несколько ЭДС-источников.

Для расчета сложных цепей применяются различные методики. Наиболее распространенной считается методика, основанная на применении второго закона Кирхгофа. В наиболее общем формате закон сформулирован таким образом: в каком-либо замкнутом контуре алгебраическая сумма ЭДС будет равнозначной такого же типа сумме падений напряжений.

Алгебраическая сумма берется по той причине, что ЭДС, действующие встречным образом в отношении друг друга, или созданные противоположно направленными токами напряжения будут иметь разные знаки.

При расчетах сложной цепи в большинстве примеров бывают известными сопротивления отдельных участков цепи и ЭДС, включенных источников. Для нахождения токов следует (на основе второго закона Кирхгофа) составить уравнения (для замкнутых контуров), в которых токи будут считаться неизвестными величинами.

К таким уравнениям также добавляются уравнения для точек разветвления, составленные по принципу первого закона Кирхгофа. При решении такой системы уравнений определяются токи. В случае с более сложными цепями, подобный метод будет достаточно громоздким, что обусловлено наличием большого числа неизвестных.

Смешанное соединение резисторов

Резистор считается устройством со стабильным значением сопротивления, что позволяет производить регулирование параметров на любых участках электроцепи. Существуют определенные разновидности соединений, к которым, в том числе, будет относиться и соединение смешанного типа для резисторов.

От применения определенного способа в конкретной схеме будет зависеть показатель неустойчивости напряжения (падение напряжения), а также распределение токов в цепи. Вариант смешанного соединения состоит из подключений последовательного и параллельного видов активных сопротивлений. Это объясняет необходимость первоочередного рассмотрения этих двух типов соединений для понимания работы других схем.

Схеме смешанного соединения будут присущи свойства схем последовательного и параллельного соединений резисторов. В таком случае элементы будут частично подключены последовательным способом, а частично – параллельным.

В качестве примера, можно привести схему с последовательным включением резисторов $R_1$ и $R_2$ и при этом параллельным подключением $R_3$. $R_4$.

В свою очередь резистор $R_4$ включается последовательно с предыдущей группой резисторов $R_1$, $R_2$ и $R_3$. Расчет сопротивления для такой цепи будет сопряженным с определенными трудностями. Актуальным здесь будет использование метода преобразования, основанного на последовательном преобразовании (поэтапно) сложной цепи в простейшую за несколько этапов:

Физические формулы и примеры вычислений

Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:

параллельное присоединение определяют по формуле Rэкв. = (R1*R2)/R1+R2;
последовательное включение вычисляют, определяя его сумму Rэкв. = R1+R2.

У смешанного соединения резистивных элементов нет конкретной формулы. Чтобы не запутаться при длительных преобразованиях, здесь допустимо воспользоваться специальной программой из интернета. Это сервис «онлайн-калькулятор». Он поможет разобраться со сложными схемами соединения, будь то треугольник, квадрат, пятиугольник или иная схематичная фигура, образованная резистивными элементами.

Понять, как работают все формулы и методы, можно на конкретной задаче. На представленном первом рисунке – смешанная электрическая схема. Она включает в себя 10 резисторов. Элементы представлены в следующих номиналах:

R1 = 1 Ом;
R2 = 2 Ом;
R3 = 3 Ом;
R4 = 6 Ом;
R5 = 9 Ом;
R6 = 18 Ом;
R7 = 2Ом;
R8 = 2Ом;
R9 = 8 Ом;
R10 = 4 Ом.

Напряжение, поданное на схему:

U = 24 В.

Требуется рассчитать токи на всех резистивных элементах.

Исходная цепь

Для расчётов применяется закон Ома:

I = U/R, подставляя вместо R эквивалентное сопротивление.

Внимание! Для решения этой задачи сначала вычисляют общее (эквивалентное) R, после чего уже рассчитывают ток в цепи и напряжение на каждом резистивном компоненте. Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения. Делают расчёты для каждого такого звена, после – всей цепи целиком

Делают расчёты для каждого такого звена, после – всей цепи целиком

Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения. Делают расчёты для каждого такого звена, после – всей цепи целиком.

На рисунке выше изображено смешанное соединение сопротивлений. Его можно разбить на три участка:

АВ – участок, имеющий две параллельных ветви;
ВС – отрезок, вмещающий в себя последовательное сопряжение;
CD – отрезок схемы с расположением трёх параллельных цепочек.

Сопротивления R2 и R3, образующие нижнюю ветку отрезка АВ, соединены последовательно, что учитывается при расчёте.

Последовательно соединённые резисторы R2 и R3

Если посмотреть на участок СD, то можно отметить смешанное включение резистивных элементов.

Смешанное включение на участке CD

Начало расчётов состоит в определении эквивалентных сопротивлений для этих смешанных фрагментов. Выполняют это в следующем порядке:

Rэкв.2,3 = R2+R3=2 + 3 = 5 Ом;
Rэкв.7,8 = (R7*R8)/R7 + R8 = (2*2)/2 + 2 = 1 Ом;
Rэкв.7,8,9 = Rэкв.7,8 + R9 = 1 + 8 = 9 Ом.

Зная значения полученных эквивалентов, упрощают первоначальную схему. Она будет иметь вид, представленный на рисунке ниже.

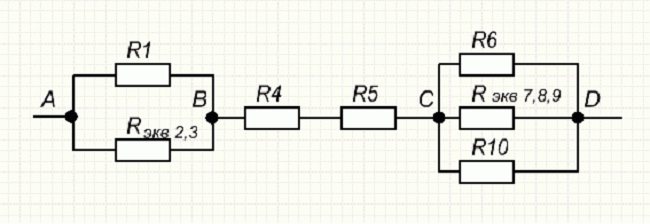
Результат первого свёртывания

Далее можно уже определить Rэкв. для участков AB, BC, CD, по формулам:

Rэкв.AB = (R1*Rэкв 2,3)/R1 + Rэкв 2,3 = (1*5)/1 + 5 = 0,83 Ом;
Rэкв.BC = R4 + R5 = 6 + 9 = 15 Ом;
1/Rэкв.CD = 1/R6 + 1/Rэкв.7,8,9 + 1/R10 = 1/18 + 1/9 + 1/4 = 0,05 + 0,11 + 0,25 = 0,41 Ом.

В результате выполненных вычислений получается эквивалентная схема, в которую входят три Rэкв. сопротивления. Она имеет вид, показанный на рисунке ниже.

Результат последующего свёртывания

Теперь можно определить эквивалентное сопротивление всей первоначальной схемы, сложив эквивалентные значения всех трёх участков:

Rэкв. = Rэкв.AB + Rэкв.BC + Rэкв.CD = 0,83 + 15 + 0,41 = 56,83 Ом.

Далее, используя закон Ома, находят ток в последнем последовательном участке:

I = U/ Rэкв. = 24/56,83 = 0,42 А.

Зная силу тока, можно найти, какое падение напряжения на рассмотренных участках AB, BC, CD. Это выполняется следующим образом:

UAB = I* Rэкв.AB= 0,42*0,83 = 0,35 В;
UBC = I* Rэкв.BC= 0,42*15 = 6,3В;
UCD = I* Rэкв.CD = 0,42*0,41 = 0,17 В.

Следующим шагом станет определение токов на параллельных отрезках AB и CD

I1 = UAB/R1 = 0,35/1 = 0,35 А;
I2 = UAB/Rэкв.2,3 = 0,35/5 = 0,07 А;
I3 = UCD/R6 = 0,17/18 = 0,009 А;
I6 = UCD/Rэкв.7,8,9= 0,17/9 = 0,02 А;
I7 = UCD/R10 = 0,17/4 = 0,04 А.

Далее, чтобы найти значения токов, проходящих через R7 и R8, нужно рассчитать напряжение на этих двух резисторах. Предварительно находят падение напряжения на R9.

U9 = R9*I6 = 8*0,02 = 0,16 В.

Теперь напряжение, падающее на Rэкв.7,8, будет разностью между U CD и U9.

U7,8 = UCD – U9= 0,17 – 0,16 = 1 В.

После этого можно уже узнать значение токов, движущихся по резисторам R7 и R8, используя формулы:

I4 = U7,8/R7 = 1/2 = 0,5 A;
I5 = U7,8/R8 = 1/2 = 0,5 A.

Рассчитывая схемы и решая задачи по нахождению значений электрических параметров, необходимо использовать эквивалентные сопротивления. С помощью такой замены сложные построения превращаются в элементарные цепи, которые сводятся к параллельным и последовательным соединениям резистивных элементов.

Соединение резисторов последовательное, параллельное, смешанное. расчет на примере