Сила лоренца

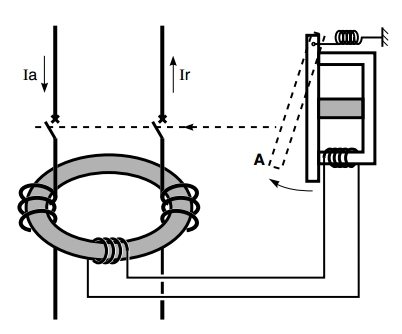
Следствия свойств силы Лоренца

Тело влетает в магнитном поле под каким-то определённым углом. Интуитивно понятно, что его величина имеет какое-то значение на характер воздействия на него поля, здесь нужно математическое выражение, чтобы стало понятнее. Следует знать, что как сила, так и скорость являются векторными величинами, то есть имеют направление. То же самое относится и к линиям магнитной напряженности. Тогда формулу можно записать следующим образом:

FЛ=qvBsinα,

sin α здесь – это угол между двумя векторными величинами: скоростью и потоком магнитного поля.

Как известно, синус нулевого угла также равен нулю. Получается, что если траектория движения частицы проходит вдоль силовых линий магнитного поля, то она никуда не отклоняется.

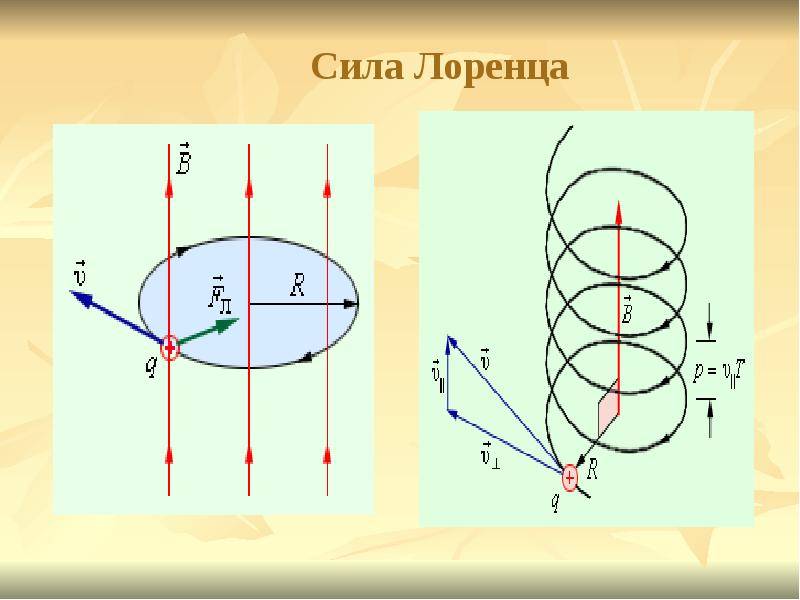
В однородном магнитном поле силовые линии имеют одинаковое и постоянное расстояние друг от друга. Теперь представим, что в таком поле перпендикулярно этим линиям движется частица. В этом случае сила Лоуренса заставит двигаться ее по окружности в плоскости, перпендикулярной силовым линиям. Чтобы найти радиус этой окружности, нужно знать массу частицы:

R=mvqB

Значение заряда не случайно взято как модуль

Это означает, что неважно, отрицательная или положительная частица входит в магнитное поле: радиус кривизны будет одинаков. Изменится только направление, в котором она полетит. Во всех остальных случаях, когда заряд имеет определенный угол α с магнитным полем, он будет двигаться по траектории, напоминающей спираль с постоянным радиусом R и шагом h

Его можно найти по формуле:

Во всех остальных случаях, когда заряд имеет определенный угол α с магнитным полем, он будет двигаться по траектории, напоминающей спираль с постоянным радиусом R и шагом h. Его можно найти по формуле:

R=mvsinαqB

h=2mvcosαqB

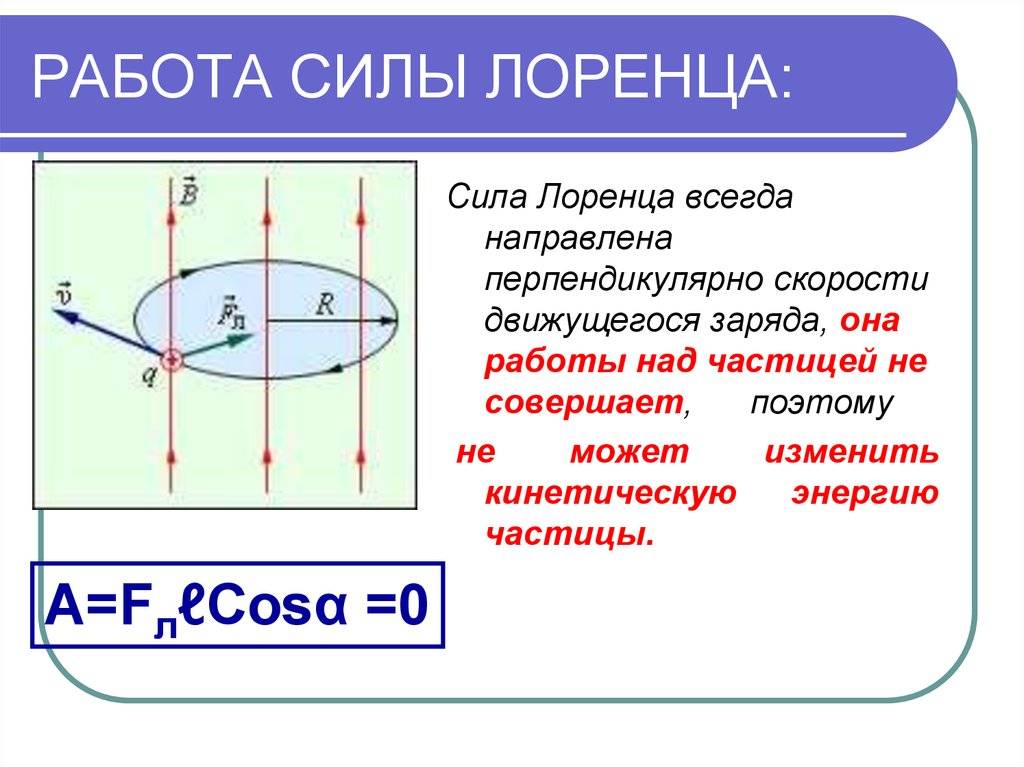
Еще одним следствием свойств этого явления является тот факт, что она не совершает никакой работы. То есть она не отдает и не забирает энергию у частицы, а лишь меняет направление ее движения.

Самая яркая иллюстрация этого эффекта взаимодействия магнитного поля и заряженных частиц – это северное сияние. Магнитное поле, окружающее нашу планету, отклоняет заряженные частицы, прилетающие от Солнца. Но так как оно слабее всего на магнитных полюсах Земли, то туда проникают электрически заряженные частицы, вызывая свечение атмосферы.

Центростремительное ускорение, которое придается частицам, используется в электрических машинах – электродвигателях. Хотя уместнее здесь говорить о силе Ампера – частном проявлении силы Лоуренса, которая воздействует на проводник.

Принцип действия ускорителей элементарных частиц также основан на этом свойстве электромагнитного поля. Сверхпроводящие электромагниты отклоняют частицы от прямолинейного движения, заставляя их двигаться по кругу.

Самое любопытное заключается в том, что сила Лоренца не подчиняется третьему закону Ньютона, который гласит, что всякому действию есть свое противодействие. Связано это с тем, что Исаак Ньютон верил, что всякое взаимодействие на любом расстоянии происходит мгновенно, однако это не так. На самом деле оно происходит с помощью полей. К счастью, конфуза удалось избежать, так как физикам удалось переработать третий закон в закон сохранения импульса, который выполняется в том числе и для эффекта Лоуренса.

Правило левой руки

Правило левой руки позволяет физикам определять направление и возврат вектора магнитной (электродинамической) энергии. Представьте себе, что наша левая рука расположена таким образом, что линии магнитного поля направлены перпендикулярно внутренней поверхности руки (так, что они проникают внутрь руки), а все пальцы за исключением большого указывают на направление протекания положительного тока, отклоненный большой палец указывает на направление электродинамической силы, действующий на положительный заряд, помещенный в это поле.

Вот так это будет выглядеть схематически.

Есть также и второй способ определения направления электромагнитной силы. Он заключается в расположении большого, указательного и среднего пальцев под прямым углом. В этом случае указательный палец будет показывать направление линий магнитного поля, средний – направление движение тока и большой – направление электродинамической силы.

Как связано магнитное поле с Буравчиком и руками

Рассматривая движение полей токовой и магнитной природы, можно легко проследить взаимную связь правила Буравчика с канонами правой и левой руки. Для более качественного сравнения этих понятий, следует рассмотреть, что они представляют собой по отдельности.

Закон Буравчика точно устанавливает направленность напряженности, вызываемой магнитными полями. При этом само поле должно размещаться в прямом направлении по отношению к проводящему материалу с электротоком.

Для более полного представления берется штопор с правой резьбой и ввинчивается по часовой стрелочке в сторону протекания тока. Направленность магнетических полей соответствует правостороннему движению штопорной рукоятки.

Правило правой руки может рассматриваться в двух вариантах. В одном из них пальцы, согнутые в кулак, охватывают неподвижный токопроводник. Они обозначают, в какую сторону смотрит вектор магнитных линий, который, как и у рукоятки Буравчика, будет по ходу часовой стрелки. Самый крупный палец отступает на 90º и показывает, в какую сторону движется ток.

Если же токопровод движется, то правая рука размещается иным способом. Ладонь устанавливается между северным и южным полюсами так, чтобы она была в перпендикулярности с силовыми линиями, проходящими через нее. Крупный палец фиксируется в вертикальном положении и показывает в сторону направленного движения проводника. Оставшиеся пальцы, протянутые вперед, смотрят в ту же сторону, что и индукционный ток. Эта установка нашла свое применение в расчетах катушечных соленоидов, оказывающих воздействие на физические свойства тока.

Отделяя друг от друга правило правой и левой руки, их физика показывает, что второй вариант, используемый в расчетах, действует по-другому. Левая ладошка размещается в таком положении, чтобы четыре пальца были направлены в сторону тока, продвигающегося по проводнику. Магнитные линии, перемещаясь от одного полюса к другому, заходят в ладошку под 90 градусов. Оттопыренный крупный палец смотрит в ту же сторону, что и сила, воздействующая на токопроводник.

Использование правила правой руки в электродинамике

Если в магнитном поле подвесить на тонком и гибком проводе рамку с током, то она будет поворачиваться и расположится определенным образом. Аналогично поведение магнитной стрелки. Это свидетельствует о векторном характере физической величины, характеризующей магнитное поле. При этом направление этого вектора будет связано с ориентацией рамки и стрелки. Физической векторной величиной, которая характеризует магнитное поле, стал вектор магнитной индукции ($\vec{B}$).

Готовые работы на аналогичную тему

• Курсовая работа Правило левой и правой руки для магнитного поля 420 руб.
• Реферат Правило левой и правой руки для магнитного поля 230 руб.
• Контрольная работа Правило левой и правой руки для магнитного поля 220 руб.

Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость Это один из главных параметров, описывающих состояние магнитного поля, поэтому необходимо уметь находить его величину и, конечно, направление.

Для определения направления вектора магнитной индукции используют:

• правило правого винта или
• правило правой руки.

Направлением вектора магнитной индукции, в месте локализации рамки с током, считают направление положительного перпендикуляра ($\vec{n}$) к этой рамке. Положительная нормаль ($\vec{n}$) будет иметь направление такое же, как направление поступательного перемещения правого винта, если его головку вращать по току в рамке (рис.1 (a)).

Рисунок 1. Определение направления вектора магнитной индукции. Автор24 — интернет-биржа студенческих работ

Так, обладая пробной рамкой с током, помещая ее в исследуемое поле, давая ей свободно вращаться в нем, можно определить, как направлен вектор магнитной индукции в каждой точке поля. Необходимо только дать рамке прийти в положение равновесия, затем использовать правило правого винта.

Ищешь идеи для учебной работы по данному предмету? Задай вопрос преподавателю и получи ответ через 15 минут! Задать вопрос

Теперь обратимся к правилу правой руки. Сожмем правую руку в неплотный кулак (рис.2). Отогнем большой палец на 90°. Руку разместим так, чтобы большой палец указывал направление течения тока, тогда согнутые остальные четыре пальца укажут направление линий магнитной индукции поля, которое создает ток. А мы помним, что касательная в каждой точке поля к силовой линии (линии магнитной индукции) указывает направление $\vec{B}$.

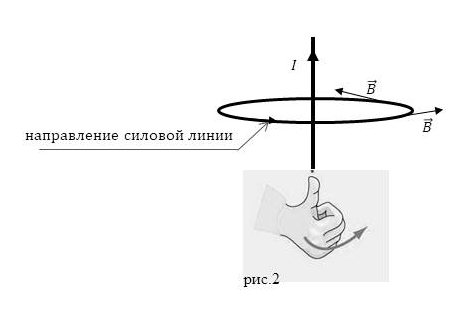
Рисунок 2. Правило правой руки. Автор24 — интернет-биржа студенческих работ

Рассмотрим соленоид. Обхватим правой ладонью его так, чтобы четыре пальца совпали с направлением тока в нем, тогда отогнутый на девяносто градусов палец укажет, как направлено магнитное поле, создаваемое у него внутри.

Нам известно, что если в магнитном поле перемещать проводник, то в этом проводнике будет возникать ток индукции. Правило правой руки можно использовать для определения направления течения тока индукции в таких проводниках. При этом:

• линии индукции магнитного поля должны входить в открытую ладонь правой руки,
• палец этой руки отогнуть на девяносто градусов, и направить по скорости перемещения проводника,
• вытянутые четыре пальца будут указывать, как направлен ток индукции.

Правилом правой руки можно воспользоваться при определении направления ЭДС индукции в контуре:

Согнутыми четырьмя пальцами правой руки охватить контур, в котором индуцируется ЭДС при изменении магнитного потока, отогнуть на девяносто градусов большой палец этой руки и направить его по направлению магнитного потока при его увеличении (или против направления магнитного потока при его уменьшении), тогда согнутые пальцы укажут на направление противоположное ЭДС.

Правило левой руки

Если определять физические величины по правилу левой руки, то ее ладонь располагается в таком положении, что четыре пальца направлены вперед, а большой отвернут в бок. Прямые пальцы указывают в сторону направления тока, а оттопыренный большой – направление устремления вектора приложенных усилий. При этом, направление индукции заходит и упирается в ладошку сверху под углом девяносто градусов.

Что определяет закон

По итогам выполнения многочисленных экспериментальных опытов было выведено определение, которое впоследствии стало именоваться правилом левой руки. Оно связало между собой направленности электротока и концентрических линий, а также влияние на проводящий материал силы магнетических полей. Живой пример отражен на картинке, где хорошо видно взаимодействие физических составляющих. Направленность силовых линий и функционирующего магнитного поля не совпадают, их действие направлено в совершенно разные места.

Когда направленность электротока и проводника будет совмещаться с линиями, то силовое влияние на проводящий материал в данном случае отсутствует. В результате, указанный постулат перестанет работать.

Сила Лоренца применение и формула

Действие электромагнитных полей порождает возникновение точечной заряженной частицы, на который воздействуют силы электрического и магнитного характера. В скомбинированном виде они получили наименование силы Лоренца.

Таким образом, сила Лоренца воздействует на любую частицу с зарядом, падающую с определенной быстротой в магнетическом поле. Степень влияния связана с электрическим зарядом частицы (q), показателем магнитной индукции (В) и быстротой падения частицы (V).

На основании полученных данных голландским ученым Хендриком Лоренцем была выведена формула: FL = |q|x V x B x sinα. Все условные обозначения приведены на рисунке.

В практической деятельности сила Лоренца получила применение в следующих областях:

• Кинескопы – электронно-лучевые или телевизионные трубки. В этих устройствах электроны, летящие в направлении экрана, отклоняются магнитным полем, которое создают специальные катушки.
• Масс-спектрографы. Определяют массы заряженных частиц, путем разделения их по удельным зарядам. Вакуумная камера помещается в магнитном поле. Заряженный частицы ускоряясь, двигаются по дуге и оставляют след на фотопластинке. Па радиусу траектории вначале определяется удельный заряд, на основании которого вычисляется и масса частицы.
• Циклотрон. Ускоряет заряженные частицы. Ускорение происходит под действием силы Лоренца, после чего траектория частиц сохраняется за счет магнитного поля. Прибор давно начали использовать в медицинских исследованиях с применением радионуклидных фармацевтических препаратов.
• Магнетрон. Электронная лампа высокой мощности для генерации микроволн, возникающих при взаимодействии электронного потока и магнитного поля. Используется с современных радиолокационных устройствах.

Сила ампера – формула

Сила Ампера непосредственно воздействует на проводник с током, расположенный внутри поля. Совсем кратко она выражается представленной формулой:

F = I x B x L x sinα, где F является силой Ампера, I – сила тока в проводнике, L – отрезок проводника, находящийся под действием магнитного поля, α – угол между направлением тока и вектором магнитной индукции.

Максимальное значение сила Ампера принимает, когда угол α становится равным 90 градусов. Единицей измерения служит ньютон (Н).

Определение направления силы Ампера выполняется с помощью правила левой руки. Ладонь смотрит вверх, четыре пальца направлены в сторону вектора движения тока. Вектор магнитной индукции перпендикулярен ладони и входит в нее. Направление силы Ампера совпадает с большим пальцем, отогнутым в сторону.

Направлением электрического тока условно считается движение от заряда с плюсом к заряду с минусом.

Урок физики в 9 классе по теме : » Решение задач по теме : «Сила Ампера. Сила Лоренца»»

Тема урока:

«Решение задач по теме «Сила Ампера. Сила Лоренца».

Место урока в системе уроков по теме:

На предыдущем уроке обучающиеся получили знания о векторе магнитной индукции, силе Ампера, силе Лоренца. Данный урок позволяет отработать навыки решения задач по формуле силы Ампера и силы Лоренца .

Цель урока:

показать теоретическую значимость закона Ампера при решении задач, научить применять полученные знания при решении задач.

Задачи урока:

• Дидактическая

  – создавать условия для усвоения нового учебного материала через проблемно-деятельностный подход.

• Образовательная

  – рассмотреть применение закона Ампера в ходе решения различных задач.

• Развивающая

  – развивать логическое мышление обучающихся при решении задач на расчёт силы Амперы и силы Лоренца.

• Воспитательная

  – прививать культуру умственной деятельности.

Планируемые результаты.

Обучающиеся должны:

• овладеть алгоритмом решения задач по данной теме.
• уметь решать задачи с применением закона Ампера, формулы для нахождения силы Лоренца .

Техническое обеспечение урока:

1. Компьютер, проектор, экран.

Дополнительное методическое и дидактическое обеспечение урока:

1. Презентация к уроку.
2. Карточки с задачами.

Мобилизующее начало урока («исходная мотивация»). Позитивный настрой на урок.

“Умение решать задачи — это практическое

искусство, подобное плаванию или катанию

на лыжах, или игре на фортепиано: научиться

этому можно, лишь подражая избранным

образцам и постоянно тренируясь”

Д. Пойа

В данной теме рассмотрим основные типы задач, а также попытаемся выделить общую методику их решений. В представленной теме можно выделить три типа задач:

1) на расчет полей (вычисление магнитной индукции, в какой либо точке магнитного поля);

2) о силовом действии магнитного поля на проводники или контур с током;

3) о силовом действии магнитного поля на движущиеся в нем заряженные частицы.

1.Фронтальный опрос:

1.Как называют физ. Величину характеризующую магнитное поле?

2. Какой буквой обозначают?

3. В каких единицах измеряют?

4. Что означает 1 Тл?

5.Какую силу называют силой Ампера? Запишите на доске формулу для расчёта Силы Ампера.

6. Как определяется направление силы Ампера? Сформулируйте правило левой руки.

7.Чему равен модуль вектора магнитной индукции?

8. Какую силу называют силой Лоренца? Запишите на доске формулу для расчёта Силы Лоренца

9. Как определяется направление силы Лоренца? Сформулируйте правило левой руки.

2. Решение задач :

Задача 1 Определить силу, с которой однородное магнитное поле действует на проводник длиной 20 см, если сила тока в нем 300 мА, расположенный под углом 45 градусов к вектору магнитной индукции. Магнитная индукция составляет 0,5 Тл.

Задача 2 Проводник с током 5 А находится в магнитном поле с индукцией 10 Тл. Определить длину проводника, если магнитное поле действует на него с силой 20Н и перпендикулярно проводнику.

Задача 3 Определить силу тока в проводнике длиной 20 см, расположенному перпендикулярно силовым линиям магнитного поля с индукцией 0,06 Тл, если на него со стороны магнитного поля действует сила 0,48 Н.

Задача 4 Проводник длиной 20см с силой тока 50 А находится в однородном магнитном поле с индукцией 40 мТл. Какую работу совершит источник тока, если проводник переместится на 10 см перпендикулярно вектору магнитной индукции (вектор магнитной индукции перпендикулярен направлению тока в проводнике).

Задача 5 Определить силу, действующую на заряд 0,005 Кл, движущийся в магнитном поле с индукцией 0,3 Тл со скоростью 200 м/с под углом 45o к вектору магнитной индукции.

Задача 6 Какова скорость заряженного тела, перемещающегося в магнитном поле с индукцией 2 Тл, если на него со стороны магнитного поля действует сила 32 Н. Скорость и магнитное поле взаимно перпендикулярны. Заряд тела равен 0,5 мКл.

3.Самостоятельная работа по карточкам

4. Рефлексия

5. Д.з.

https://youtube.com/watch?v=eMa11WYguzk

https://youtube.com/watch?v=7IUpOAsKKvI

https://youtube.com/watch?v=mmAB-_2VYPk

Взаимодействие токов

Рассмотрим два случая. Первый – ток течет по прямому проводу. Второй – по круговому витку. Как мы знаем, ток создает магнитное поле.

В первом случае магнитная индукция провода с током I на расстоянии R от него считается по формуле:

Мю – магнитная проницаемость вещества, мю с индексом ноль – магнитная постоянная.

Во втором случае магнитная индукция в центре кругового витка с током равна:

Также при решении задач может пригодиться формула для магнитного поля внутри соленоида. Соленоид – это катушка, то есть множество круговых витков с током.

Пусть их количество – N, а длина самого соленоилда – l. Тогда поле внутри соленоида вычисляется по формуле:

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Что такое линии магнитной индукции

Магнитное поле определено напряженностью в каждой точке его пространства. Кривые, объединяющие точки поля с равными по модулю напряженностями называются линиями магнитной индукции. Напряжённость магнитного поля в конкретной точке — силовая характеристика и для ее оценки применяется вектор магнитного поля В. Его направление в конкретной точке на линии магнитной индукции происходит по касательной к ней.

В случае, если на точку в пространстве влияет несколько магнитных полей, то напряженность определяется суммированием векторов магнитной индукции каждого действующего магнитного поля. При этом  напряженность в конкретной точке суммируется по модулю, а вектор магнитной индукции определяется как сумма векторов всех магнитных полей.

Несмотря на то, что линии магнитной индукции невидимые, они обладают определенными свойствами:

• Принято считать, что силовые линии магнитного поля выходят на полюсе (N), а возвращаются с (S).
• Направление вектора магнитной индукции происходит по касательной к линии.
• Несмотря на сложную форму, кривые не пересекаются и обязательно замыкаются.
• Магнитное поле внутри магнита однородно и плотность линий максимальна.
• Через точку поля проходит только одна линия магнитной индукции.

Уравнение (единицы СИ)

Заряженная частица

Силой F действующий на частицу электрического заряда q с мгновенной скоростью v, из-за внешнего электрического поля E и магнитного поля B, дают:

где векторный продукт креста. Все жирные количества – векторы. Более явно заявленный:

в котором r – вектор положения заряженной частицы, t – время, и сверхточка – производная времени.

Положительно заряженная частица будет ускорена в той же самой линейной ориентации как область E, но изогнется перпендикулярно и к мгновенному скоростному вектору v и к области B согласно правому правилу (подробно, если большой палец правых пунктов вдоль v и указательный палец вдоль B, то средний палец указывает вдоль F).

Термин qE называют электрической силой, в то время как термин qv B называют магнитной силой. Согласно некоторым определениям, термин «сила Лоренца» относится определенно к формуле для магнитной силы с полной электромагнитной силой (включая электрическую силу) данный некоторое другое (нестандартное) имя. Эта статья не будет следовать этой номенклатуре: В дальнейшем термин «сила Лоренца» отнесется только к выражению для полной силы.

Магнитный компонент силы силы Лоренца проявляется как сила, которая действует на находящийся под напряжением провод в магнитном поле. В том контексте это также называют лапласовской силой.

Непрерывное распределение обвинения

Для непрерывного распределения обвинения в движении уравнение силы Лоренца становится:

где dF – сила на маленькой части распределения обвинения с обвинением dq. Если обе стороны этого уравнения разделены на объем этой маленькой части распределения обвинения dV, результат:

где f – плотность силы (сила за единичный объем), и ρ – плотность обвинения (обвинение за единичный объем). Затем, плотность тока, соответствующая движению континуума обвинения, является

таким образом, непрерывный аналог уравнению –

Полная сила – интеграл объема по распределению обвинения:

Устраняя ρ и J, используя уравнения Максвелла и управляя использованием теорем векторного исчисления, эта форма уравнения может использоваться, чтобы получить тензор напряжения Максвелла σ, в свою очередь это может быть объединено с вектором Пойнтинга S, чтобы получить электромагнитный тензор энергии напряжения T используемый в Общей теории относительности.

С точки зрения σ и S, другим способом написать силу Лоренца (за единицу 3-й объем) является

где c – скорость света и ∇ · обозначает расхождение области тензора. Вместо суммы обвинения и его скорости в электрических и магнитных полях, это уравнение связывает энергетический поток (поток энергии в единицу времени за расстояние единицы) в областях к силе, проявленной на распределении обвинения. Дополнительную информацию см. в Ковариантной формулировке классического электромагнетизма.

История

Современное понятие электрических и магнитных полей сначала возникло в теориях Майкла Фарадея, особенно его идея линий силы, позже чтобы быть данным полное математическое описание лорда Келвина и Джеймса Клерка Максвелла. С современной точки зрения возможно определить в формулировке Максвелла 1865 года его уравнений поля форму уравнения силы Лоренца относительно электрических токов, однако, во время Максвелла, не было очевидно, как его уравнения имели отношение к силам при перемещении заряженных объектов. Дж. Дж. Томсон был первым, чтобы попытаться получить из уравнений поля Максвелла электромагнитные силы на перемещении заряженный объект с точки зрения свойств объекта и внешних областей. Заинтересованный определением электромагнитного поведения заряженных частиц в лучах катода, Thomson опубликовал работу в 1881 в чем, он дал силу на частицах из-за внешнего магнитного поля как

Thomson получил правильную каноническую форму формулы, но, из-за некоторых просчетов и неполного описания тока смещения, включал неправильный коэффициент пропорциональности половины перед формулой. Именно Оливер Хивизид, изобрел современное векторное примечание и применил их к уравнениям поля Максвелла, которые в 1885 и 1889 фиксировали ошибки происхождения Thomson и достигли правильной формы магнитной силы на перемещении заряженный объект. Наконец, в 1892, Хендрик Лоренц получил современную форму формулы для электромагнитной силы, которая включает вклады в полную силу и от электрического и от магнитных полей. Лоренц начал, оставив описания Maxwellian эфира и проводимости. Вместо этого Лоренц сделал различие между вопросом и luminiferous эфиром и стремился применить уравнения Максвелла в микроскопическом масштабе. Используя версию Хивизида уравнений Максвелла для постоянного эфира и применения лагранжевой механики (см. ниже), Лоренц достиг правильного, и заполните форму закона о силе, который теперь носит его имя.

Похожие записи:

Что лучше установить в щитке: «дифавтомат» или узо? Как выбрать катушку для спиннинга? (+видео) Укладка ламината на систему теплого водяного пола Разновидности уличных светодиодных светильников Какие светильники оптимально подходят для ванной комнаты Что такое герконовый датчик и где он применяется?