Как выбрать катушку для спиннинга? (+видео)

Особенности расчёта индуктивных элементов с сердечниками

В отличие от индуктивных элементов без сердечников, при расчёте которых учитывался магнитный поток пронизывающий только проводник с током, магнитный поток индуктивных элементов с сердечниками практически полностью замыкается на сердечники. Поэтому при расчёте индуктивности таких элементов необходимо учитывать размеры сердечника и материал, из которого он изготовлен, то есть его магнитную проницаемость.

Обобщённую формулу для расчёта индуктивных элементов с сердечниками можно выразит с помощью следующего выражения

где ω – количество витков катушки,

R_M – сопротивление магнитной цепи,

μ_а – абсолютная магнитная проницаемость вещества, из которого изготовлен сердечник,

S_M – площадь поперечного сечения сердечника,

l_M – длина средней магнитной силовой линии,

Таким образом, зная размеры сердечника можно достаточно просто вычислить индуктивность. Однако в связи с такой простотой выражения и разбросом магнитной проницаемости материала сердечника, погрешность в расчёте индуктивности составит 25 %.

Для сердечников, имеющих сложную конструктивную конфигурацию, вводится понятие эффективных (эквивалентных) размеров, которые учитывают особенности формы сердечников: эффективный путь магнитной линии l_e и эффективная площадь поперечного сечения S_e сердечника. Тогда индуктивность катушки с сердечником будет вычисляться по формуле

где ω – количество витков катушки,

μ – магнитная постоянная, μ = 4π*10-7,

μ_r – относительная магнитная проницаемость вещества,

S_e – эффективная площадь поперечного сечения сердечника,

l_e – эффективный путь магнитной линии сердечника.

Таким образом, расчёт индуктивности индуктивных элементов с сердечниками сводится к нахождению эффективных размеров сердечника. Для упрощения нахождения данных размеров сердечника ввели вспомогательные величины, называемые постоянные сердечников:

С₁ – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника, измеряется в мм-1;

С₂ – вторая постоянная сердечника, которая равна сумме отношений длин однородных по сечению участков сердечника к квадрату своего сечения, измеряется в мм-3;

где N – количество разнородных участков сердечника,

l_N – длина N – го участка сердечника,

S_N – площадь N – го участка сердечника.

Тогда величины S_e и l_e определятся из следующих выражений

Кроме индуктивности с помощью постоянных С₁ и С­₂ определяют эффективный объём V_e, который требуется для определения параметоров силовых индуктивных элементов – трансформаторов и дросселей. Если же есть необходимость рассчитать только индуктивность L, то используют только постоянную С₁ по следующему выражению

где ω – количество витков катушки,

μ – магнитная постоянная, μ = 4π*10-7,

μ_r – относительная магнитная проницаемость вещества,

С₁ – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника.

Несмотря на довольно сложные формулировки и формулы, вычисление индуктивности по ним достаточно простое.

Выпускается достаточно много типов сердечников, которые обладают различными конструктивными особенностями и свойствами, рассмотрим некоторые из них.

Эквивалентная схема реальной катушки индуктивности

Каждый дроссель можно представить в виде эквивалентной схемы.

Данная схема состоит из элементов:

• Rw – сопротивление обмотки с выводами;
• L – индуктивность;
• Cw – паразитная ёмкость;
• Rl – сопротивление потерь.

Изготавливая индуктивный элемент, стремятся снизить величину сопротивления потерь, паразитную ёмкость. При работе катушки на низкой частоте учитывают сопротивление её обмотки Rw. На таких частотах действуют токи большой величины.

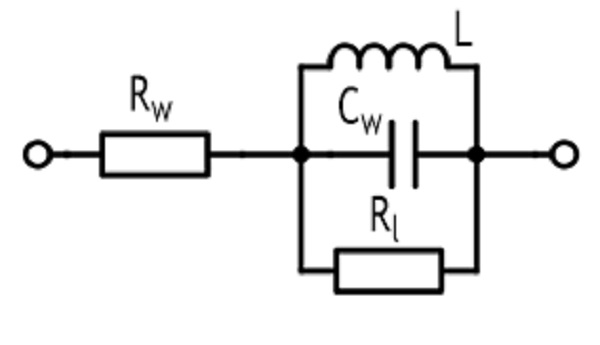
Эквивалентная схема дросселя

Правильно рассчитанная катушка индуктивности будет иметь высокую добротность (180-300) и стабильность работы при влиянии внешних условий (температуры и влажности). Зная способы различной намотки и манипуляции с шагом, можно уменьшить влияние паразитных факторов.

Катушка Тесла своими руками

Как изготовить что-то эффектное по изобретениям Тесла? Увидев его идеи и изобретения, будет сделана катушка Тесла своими руками.

Это трансформатор, создающий высокое напряжение. Вы можете трогать искру, зажигать лампочки.

Для изготовления нам нужен медный провод в эмали диаметром 0,15 мм. Подойдет любой от 0,1 до 0,3 мм. Вам нужно порядка двухсот метров. Его можно достать из различных приборов, допустим, из трансформаторов, либо купить на рынке, это будет лучше. Еще вам понадобится несколько каркасов. Во-первых, это каркас для вторичной обмотки. Идеальный вариант – это 5 метровая канализационная труба, но, подойдет что угодно диаметром от 4 до 7 см, длиной 15-30 см.

Для первичной катушки вам понадобится каркас на пару сантиметров больше первого. Также понадобится несколько радиодеталей. Это транзистор D13007, либо его аналоги, небольшая плата, несколько резисторов, 5, 75 килоом 0,25 Вт.

Проволоку мотаем на каркас около 1000 витков без перехлестов, без больших промежутков, аккуратно. Можно управиться за 2 часа. Когда намотка закончена, намазываем обмотку лаком в несколько слоев, либо другим материалом, чтобы она не пришла в негодность.

Намотаем первую катушку. Она мотается на каркасе больше и мотается проводом порядка 1 мм. Здесь подойдет провод, порядка 10 витков.

Если изготавливать трансформатор простого типа, то состав его – это две катушки без сердечника. На первой обмотке около десяти витков толстого провода, на второй – не менее тысячи витков. При изготовлении, катушка Тесла своими руками имеет коэффициент в десятки раз больше, чем число витков второй и первой обмоток.

Выходное напряжение трансформатора будет достигать миллионы вольт. Это дает красивое зрелище в несколько метров.

Сложно намотать катушку Тесла своими руками. Еще труднее создать облик катушке для привлечения зрителей.

Сначала необходимо определиться с питанием в несколько киловольт, закрепить к конденсатору. При лишней емкости изменяется значение параметров диодного моста. Далее, подбирается промежуток искры для создания эффекта.

• Два провода скрепляются, оголенные концы были повернуты в сторону.
• Выставляется зазор из расчета пробивания немного большем напряжении данной разности потенциалов. Для переменного тока разность потенциалов будет выше определенного.
• Подключается питание катушке Тесла своими руками.
• Наматывается вторичная обмотка 200 витков на трубу из изоляционного материала. Если все изготовлено по правилам, то разряд будет хороший, с ветвями.
• Заземление второй катушки.

Получается катушка Тесла своими руками, которую можно изготовить дома, владея элементарными познаниями в электричестве.

Расчёт катушки с П–образным сердечником прямоугольного сечения

В отличие от тороидальных сердечников, П – образные сердечники выполняются разборными и состоят из двух частей. Существует две модификации таких сердечников: состоящие из двух П – образных частей и из П – образной и прямоугольной замыкающей пластины.

Такие сердечники применяются в импульсных трансформаторах и трансформаторах строчной развертки и, обладая большой магнитной проницаемостью, обеспечивают малую потребляемую мощность.

П-образный сердечник с прямоугольным сечением: из двух П-образных частей (слева) и П-образной части с замыкающей прямоугольной пластиной (справа).

https://youtube.com/watch?v=Y8-saxraVlk

Для расчёта параметров сердечника рассмотрим сечение замкнутого П-образного сердечника

Сечение П-образного прямоугольного сердечника.

Данный сердечник состоит из нескольких участков l

имеющих различное сечение S

,. Тогда коэффициенты С

составят

Неизвестные величины можно найти следующим образом

Пример. Необходимо рассчитать индуктивность обмотки трансформатора, выполненного на П-образном сердечнике фирмы Epcos типа UU93/152/16, выполненного из двух П-образных половинок, материал сердечника N87 μr = 1950, количество витков ω = 150.

Сердечник Epcos U93/76/16.

Таким образом коэффициент С1 и индуктивность L составят

Кроме П-образных катушек с прямоугольным сечение, широко применяются П-образные катушки с круговым сечением. Они также состоят из двух П-образных частей

П-образный сердечник с круговым сечением.

Для расчёта рассмотрим сечение замкнутого сердечника состоящего из двух пловинок.

Сечение П-образного сердечника с круговым сечением.

Аналогично сердечнику с прямоугольным сечением выделим пять участков длины сердечника с различным сечением и расчёт соответственно тоже. Площадь круговых участков считается по известной формуле для площади круга, влиянием технологических пазов и отверстий можно пренебречь

Сердечник типа SDMR 40 UY20.

Параметры сердечника для расчёта составят

На сегодня всё. Продолжение смотри в следующей статье.

https://youtube.com/watch?v=BhnJnkggaXY

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

СДЕЛАЕМ УПРОЩЕННЫЙ РАСЧЕТ ТРАНСФОРМАТОРА 220/36 ВОЛЬТ.

Мощность во вторичной цепи: Р_2 = U_2 · I_2 = 60
ватт

Где:Р_2
– мощность на выходе трансформатора, нами задана 60 ватт
;

U
_2
– напряжение на выходе трансформатора, нами задано 36 вольт
;

I
_2
– ток во вторичной цепи, в нагрузке.

КПД трансформатора мощностью до 100 ватт
обычно равно не более η = 0,8
.КПД определяет, какая часть мощности потребляемой от сети идет в нагрузку. Оставшаяся часть идет на нагрев проводов и сердечника. Эта мощность безвозвратно теряется.

Определим мощность потребляемую трансформатором от сети с учетом потерь:

Р_1 = Р_2 / η = 60 / 0,8 = 75 ватт
.

Мощность передается из первичной обмотки во вторичную через магнитный поток в магнитопроводе.Поэтому от значения Р_1

, мощности потребляемой от сети 220
вольт,
зависит площадь поперечного сечения магнитопровода S
.

Магнитопровод – это сердечник Ш – образной или О – образной формы, набранный из листов трансформаторной стали. На сердечнике будут располагаться первичная и вторичная обмотки провода.

Площадь поперечного сечения магнитопровода рассчитывается по формуле:

S = 1,2 · √P_1.

Где:S
– площадь в квадратных сантиметрах,P
_1 – мощность первичной сети в ваттах.

S = 1,2 · √75 = 1,2 · 8,66 = 10,4 см².

По значению S
определяется число витков w
на один вольт по формуле:

w = 50/S

В нашем случае площадь сечения сердечника равна S = 10,4 см.кв.

w = 50/10,4 = 4,8
витка на 1 вольт.

Рассчитаем число витков в первичной и вторичной обмотках.

Число витков в первичной обмотке на 220 вольт:

W1 = U_1 · w = 220 · 4.8 = 1056 витка.

Число витков во вторичной обмотке на 36 вольт:

W2 = U_2 · w = 36 · 4,8 = 172.8 витков
,

округляем до 173 витка
.

В режиме нагрузки может быть заметная потеря части напряжения на активном сопротивлении провода вторичной обмотки. Поэтому для них рекомендуется число витков брать на 5-10 % больше рассчитанного. Возьмем W2 = 180 витков.

Величина тока в первичной обмотке трансформатора:

I_1 = P_1/U_1 = 75/220 = 0,34 ампера
.

Ток во вторичной обмотке трансформатора:

I_2 = P_2/U_2 = 60/36 = 1,67 ампера.

Диаметры проводов первичной и вторичной обмоток определяются по значениям токов в них исходя из допустимой плотности тока, количества ампер на 1 квадратный миллиметр площади проводника. Для трансформаторов плотность тока,для медного провода,

принимается 2 А/мм² .

При такой плотности тока диаметр провода без изоляции в миллиметрах определяется по формуле: d = 0,8√I
.

Для первичной обмотки диаметр провода будет:

d_1 = 0,8 · √1_1 = 0,8 · √0,34 = 0,8 · 0,58 = 0,46 мм. Возьмем 0,5 мм
.

Диаметр провода для вторичной обмотки:

d_2 = 0,8 · √1_2 = 0,8 · √1,67 = 0,8 · 1,3 = 1,04 мм. Возьмем 1,1 мм.

ЕСЛИ НЕТ ПРОВОДА НУЖНОГО ДИАМЕТРА,
то можно взять несколько, соединенных параллельно, более тонких проводов. Их суммарная площадь сечения должна быть не менее той, которая соответствует рассчитанному одному проводу.

Площадь поперечного сечения провода определяется по формуле:

s = 0,8 · d².

где
: d – диаметр провода
.

Например: мы не смогли найти провод для вторичной обмотки диаметром 1,1
мм.

Площадь поперечного сечения провода диаметром 1,1
мм. равна:

s = 0,8 · d² = 0,8 · 1,1² = 0,8 · 1,21 = 0,97 мм²
.

Округлим до 1,0
мм².

Изтаблицывыбираем диаметры двух проводов сумма площадей сечения которых равна 1.0 мм².

Например, это два провода диаметром по 0,8 мм
. и площадью по0,5 мм²
.

Или два провода: – первый диаметром 1,0 мм
. и площадью сечения 0,79 мм²
,– второй диаметром 0,5 мм
. и площадью сечения 0,196 мм²
.что в сумме дает: 0,79 + 0,196 = 0,986 мм².

Намотка катушки ведется двумя проводами одновременно, строго выдерживается равное количество витков обоих проводов. Начала этих проводов соединяются между собой. Концы этих проводов также соединяются.

Получается как бы один провод с суммарным поперечным сечением двух проводов.

Смотрите статьи:– «Как намотать трансформатор на Ш-образном сердечнике».– «Как изготовить каркас для Ш – образного сердечника».

Электрический аппарат – трансформатор используется для преобразования поступающего переменного напряжения в другое – исходящее, к примеру: 220 В в 12 В (конкретно это преобразование достигается использованием понижающего трансформатора). Прежде чем разбираться с тем, как рассчитать трансформатор, вы в первую очередь должны обладать знаниями о его структуре.

Простейший трансформатор является компоновкой магнитопровода и обмоток 2-х видов: первичной и вторичной, специально намотанных на него. Первичная обмотка воспринимает подающееся переменное напряжение от сети (н-р: 220 В), а вторичная обмотка, посредством индуктивной связи создает другое переменное напряжение. Разность витков в обмотках влияет на выходное напряжение.

Методы расчета индуктивностей

Наиболее полно теоретические основы методов расчета индуктивностей изложены в справочной книге: «». Здесь же хотелось бы немного систематизировать подходы к расчету индуктивностей.

Прежде всего отметим, что расчет индуктивности можно вести двумя способами:∙ Численный метод с различной степенью упрощения задачи ∙ Расчет по упрощенным эмпирическим формулам

Эмпирический подход предполагает подбор (подгонку) относительно несложных аппроксимирующих формул по результатам измерений индуктивности реальных катушек. Расчет по упрощенным эмпирическим формулам имеет ограничения в точности и применим только к катушкам с определенной геометрией намотки. Большинство таких формул можно найти здесь. Несмотря на невысокую точность, такой расчет чаще всего вполне достаточен в радиолюбительской практике.

Численные методы основываются на реальных физических моделях катушек индуктивности и их, в свою очередь, можно разбить на две категории:

1. Расчет в программах основанных на фундаментальных законах классической электродинамики, так называемых электромагнитных симуляторах. К ним можно отнести , , , и т.п. Эти программы используют специальные численные методы, такие как и . Расчет в таких программах довольно точен, позволяет учесть множество нюансов, рассчитать катушку произвольной формы, однако требует огромных ресурсов компьютера. Применяется при научном анализе или если катушка работает в режиме, когда ее нельзя представлять как сосредоточенный элемент []
2. Численные методы расчета, основанные на фундаментальных формулах физики, применимых к круговым проводникам, выведенных в XIX веке . Позволяют провести расчет более точно, чем по эмпирическим формулам, но не требуют запредельных аппаратных ресурсов компьютера. На них следует остановится подробнее, т.к их и использует Coil32…

Расчет индуктивности в программе Coil32 основан на модели Максвелла, в которой катушка представляется как множество соосных бесконечно тонких круговых проводников.Из следует, что силовые линии магнитного поля всегда замкнуты. Из этого следует, что магнитный поток порожденный круговым контуром с током весь проходит через поверхность, ограниченную этим контуром. Это обстоятельство отражено в следующей формуле:

Из этой формулы можно вывести определение для собственной индуктивности кругового проводника через двойной контурный интеграл Ф.Е.Неймана для взаимоиндукции :

Как показал Д.К.Максвелл, для двух бесконечно тонких круговых соосных проводников этот интеграл имеет однозначное решение, которое выглядит следующим образом:

, где:

• M — взаимоиндукция;
• r₁, r₂ — радиусы двух бесконечно тонких круговых проводников;
• x — расстояние между центрами кругов, ограниченных этими проводниками;
• K,E — , соответственно первого и второго рода;

Численный метод расчета по формуле Максвелла сводится к численным методам решения эллиптических интегралов.

По формуле Максвелла можно рассчитывать как индуктивность многослойных и однослойных катушек, так и взаимную индуктивность двух отдельных катушек. Погрешности модели, связанные с допущением, что провод бесконечно тонкий и представляет собой набор круговых проводников (хотя на самом деле — это спираль), можно уменьшить с помощью соответствующих поправок.

Рассчитывая взаимоиндукцию проводника «самого на себя», т.е. его самоиндукцию (собственную индуктивность), Максвелл использует понятие — «среднее геометрическое расстояние» — GDM (g), для круглого провода:

g = e0.25*r_w, где r_w — радиус провода.

Очень важен следующий момент. Вся вышеприведенная логика рассуждений и вывода формул, начиная от формулы Неймана, справедлива в случае равномерного распределения плотности тока вдоль катушки. В подавляющем большинстве практических случаев так и есть. Однако если катушка работает вблизи частот собственного резонанса, начинает проявляться неравномерность распределения плотности тока по проводнику! Другими словами, начинает проявляться зависимость индуктивности от частоты, которая в наших расчетах не учитывается. Поэтому индуктивность катушки можно рассчитать корректно только на частотах не превышающих 60-70% от частоты ее собственного резонанса. Таким образом Coil32 не годится для точных расчетов, например, катушек Тесла или спиральных резонаторов. В этом случае и в случае если катушка работает в режиме выше частоты собственного резонанса — ее нужно представлять только в виде модели длинной линии и рассчитывать в программах-электромагнитных симуляторах, либо пользоваться специальными эмпирическими формулами.

Ссылки:

1. D W Knight 2013
2. Robert Weaver 2012
3. Marc T. Thompson 1999
4. M.A.Bueno A K T Assis 1995

Какие параметры есть у катушки

От того, где будет применяться индуктивный элемент и на какой частоте работать, зависит его исполнение. Имеются общие параметры:

• L – индуктивность;
• R пот – сопротивление потерь;
• Q – добротность;
• свой резонанс и паразитарная ёмкость;
• коэффициенты ТКИ и ТКД.

От чего зависит индуктивность

Индуктивность (коэффициент самоиндукции) L – это главная электрическая характеристика элемента, которая показывает количество накапливаемой дросселем энергии при передвижении тока. Величина энергии в катушки тем выше, чем больше её индуктивность. Единица измерений L – 1 Гн.

При взаимодействии тока и магнитного поля в обмотке возникают вредные явления. Они способствуют возникновению потерь, которые обозначают R пот. Формула потерь имеет вид:

R пот = rω + rd + rs + re.

Слагаемые формулы – это потери:

• rω – в проводах;
• rd – в диэлектрике;
• rs – в сердечнике;
• re – на вихревые токи.

В результате таких потерь импеданс индуктивного двухполюсника нельзя назвать целиком реактивным.

Добротность двухполюсника определяется по формуле:

Q = ω*L/R пот,

где ω*L = 2π*L – реактивное сопротивление.

При наматывании витков элемента между ними возникает ненужная ёмкость. Из-за этого дроссель превращается в колебательный контур с собственным резонансом.

ТКИ – показатель, описывающий зависимость L от Т0С.

ТКД – показатель, описывающий зависимость добротности от Т0С.

Информация. Изменение основных параметров индуктивного двухполюсника зависит от коэффициентов ТКИ, ТКД, а также от времени и влажности.

Калькулятор взаимной индукции

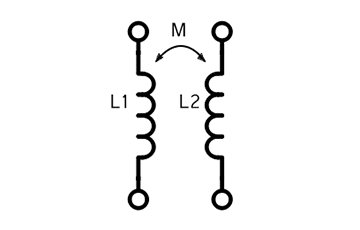
Этот калькулятор определяет взаимоиндукцию двух связанных катушек индуктивности.

Пример.

Рассчитать взаимную индуктивность двух расположенных рядом катушек индуктивности 10 мкГн и 5 мкГн с коэффициентом связи 0,5.

Входные данные

Индуктивность первой катушки, L1

генри (Гн)миллигенри (мГн)микрогенри (мкГн)наногенри (нГн)пикогенри (пГн) Индуктивность второй катушки, L2

миллигенри (мГн)

Коэффициент связи, k

0 ≤ k

≤ 1

Выходные данные

ВзаимоиндукцияM миллигенри (мГн)

Введите величины индуктивностей и коэффициента связи, выберите единицы индуктивности в генри (Гн), миллигенри (мГн), микрогенри (мкГн) или пикогенри (пГн) и нажмите кнопку Рассчитать

В токоизмерительных клещах с разъемным магнитопроводом для безопасного измерения тока без необходимости подключать прибор к схеме используется измерительный трансформатор. В приборе используется явление взаимной индукции. На разъемном магнитопроводе надета катушка, являющаяся вторичной обмоткой измерительного трансформатора. Первичной «обмоткой» является охватываемый магнитопроводом провод с током. Электродвижущая сила, возникающая в катушке на магнитопроводе, пропорциональна току, текущему в проводнике, охваченном клещами. Прибор измеряет напряжение на зажимах катушки и указывает на дисплее значение измеряемого тока.

Калькулятор определит взаимоиндукцию M двух связанных катушек индуктивности по формуле:

где k — коэффициент связи, L₁ — индуктивность первой катушки и L₂ — индуктивность второй катушки. Коэффициент связи определяется как отношение взаимоиндукции двух катушек к максимально возможному значению их взаимоиндукции. Коэффициент связи изменяется в пределах от 0 до 1 и зависит от близости катушек или обмоток, материала их сердечника, их взаимной ориентации, формы и количества витков. У слабо связанных катушек или обмоток коэффициент связи k 0.5. Если две катушки плотно намотаны одна над другой на общем ферромагнитном сердечнике, их связь почти идеальна и значение коэффициента связи k приближается к единице. Если же расстояние между катушками велико, значение k очень мало и приближается к нулю.

Тороидальные трансформатор и дроссель в импульсном блоке питания

Пример расчетов. Коэффициент связи двух катушек с индуктивностью 2 мкГн и 3 мкГн равен 0,5. Взаимоиндукция в микрогенри определяется как

Две катушки с взаимной индукцией на принципиальной схеме

При увеличении электрического тока, протекающего через катушку индуктивности L₁ от внешней цепи, вокруг катушки создается увеличивающееся магнитное поле, в котором сохраняется энергия. При уменьшении тока магнитное поле также уменьшается. При этом на выводах катушки возникает напряжение (ЭДС самоиндукции) в направлении, противоположном направлению тока, и сохраняемая в магнитном поле энергия отдается обратно во внешнюю цепь. Если рядом с первой катушкой поместить вторую катушку L₂, то магнитное поле, возникшее в первой катушке, создаст напряжение во второй катушке. Если общее магнитное поле пронизывает несколько катушек, говорят, что у них имеется взаимная индукция. Она обычно обозначает буквой M и измеряется в единицах индуктивности (генри).

Взаимоиндукция в вашем автомобиле: для создания искры в свечах зажигания используется катушка зажигания, представляющая собой трансформатор с высоким коэффициентом трансформации. Когда ток через первичную обмотку с малым числом витков прерывается, очень большая ЭДС возникает во вторичной обмотке с большим числом витков, которая достаточна для создания искры в зазоре автомобильной свечи зажигания

В обратной ситуации, если ток течет в катушке L₂, а наводится ток в катушке L₁, взаимоиндукция будет той же. Отметим, что электродвижущая сила (ЭДС) возникает только при изменении тока, причем чем быстрее изменяется ток, тем больше будет ЭДС. То есть, ЭДС взаимной индукции прямо пропорциональна скорости изменения тока

Явление взаимной индукции используется в трансформаторах, электродвигателях, генераторах и других устройствах, в которых для функционирования необходимо взаимодействие с магнитным полем. В то же время взаимоиндукция часто бывает нежелательной, когда возникает паразитная индуктивная связь между проводниками в схеме или даже между силовыми кабелями и металлическими кабельными каналами, в которых они помещены.

Принцип катушки Тесла

Чтобы понять, как работает катушка Тесла, нужно запомнить правило по электронике: лучше раз увидеть, чем сто услышать. Схема катушки Тесла простая. Это простейшее устройство катушки Тесла создает стримеры.

Из высоковольтного конца катушки Тесла вылетает стример фиолетового цвета. Вокруг нее есть странное поле, которое заставляет светиться люминесцентную лампу, которая не подключена и находится в этом поле.

Стример – это потери энергии в катушке Тесла. Никола Тесла старался избавляться от стримеров за счет того, чтобы подсоединить его к конденсатору. Без конденсатора стримера нет, а лампа горит ярче.

Катушку Тесла можно назвать игрушкой, кто показывает интересный эффект. Она поражает людей своими мощными искрами. Конструировать трансформатор – дело интересное. В одном устройстве совмещаются разные эффекты физики. Люди не понимают, как функционирует катушка.

Катушка Тесла имеет две обмотки. На первую подходит напряжение переменного тока, создающее поле потока. Энергия переходит во вторую катушку. Похожее действие у трансформатора.

Вторая катушка и Cs образуют дают колебания, суммирующие заряд. Некоторое время энергия держится в разности потенциалов. Чем больше вложим энергии, на выходе будет больше разности потенциалов.

Схема замещения катушки с последовательным соединением элементов

В схеме с последовательным соединением элементов реальная катушка характеризуется активным сопротивлением R и индуктивностью L.

Активное сопротивление определяется величиной мощности потерь

R = P/I2

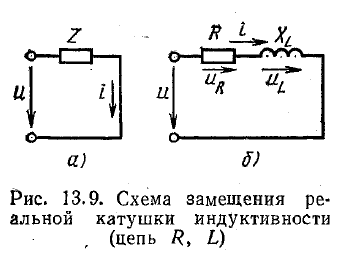
а индуктивность — конструкцией катушки. Предположим, что ток в катушке (рис. 13.9, а) выражается уравнением i = Imsinωt. Требуется определить напряжение в цепи и мощность. При переменном токе в катушке возникает э. д. с. самоиндукции eL поэтому ток зависит от действия приложенного напряжения и эдс eL. Уравнение электрического равновесия цепи, составленное по второму закону Кирхгофа, имеет вид:

Приложенное к катушке напряжение состоит из двух слагаемых,одно из которых uR равно падению напряжения в активном сопротивлении, а другое uL уравновешивает эдс самоиндукции.

В соответствии с этим катушку в схеме замещения можно представить активным и индуктивным сопротивлениями, соединенными последовательно (рис. 13.9, б). Дополнительно заметим, что оба слагаемых в правой части равенства (13.12) являются синусоидальными функциями времени. Согласно выводам полученных в этих предыдущих двух (первая, вторая) статьях получим — uR совпадает по фазе с током, UL опережает ток на 90°.

Поэтому:

u = R*Imsinωt + ωLImsin(ωt+π/2).

Реактивное сопротивление катушки индуктивности.

При протекании переменного тока I в катушке, магнитное поле создаёт в её витках ЭДС, которая препятствует изменению тока.
При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении – положительна и препятствует его убыванию,
оказывая таким образом сопротивление изменению тока на протяжении всего периода.

В результате созданного противодействия, на выводах катушки индуктивности в противофазе формируется напряжение U, подавляющее ЭДС,
равное ей по амплитуде и противоположное по знаку.

При прохождении тока через нуль, амплитуда ЭДС достигает максимального значения,
что образует расхождение во времени тока и напряжения в 1/4 периода.

Если приложить к выводам катушки индуктивности напряжение U, ток не может начаться мгновенно по причине противодействия ЭДС,
равного -U, поэтому ток в индуктивности всегда будет отставать от напряжения на угол 90°. Сдвиг при отстающем токе называют положительным.

Запишем выражение мгновенного значения напряжения u исходя из ЭДС (ε), которая
пропорциональна индуктивности L и скорости изменения тока: u = -ε = L(di/dt).
Отсюда выразим синусоидальный ток .

Интегралом функции sin(t) будет -соs(t), либо равная ей функция sin(t-π/2).
Дифференциал dt функции sin(ωt) выйдет из под знака интеграла множителем 1/ω.
В результате получим выражение мгновенного значения тока со
сдвигом от функции напряжения на угол π/2 (90°).
Для среднеквадратичных значений U и I в таком случае можно записать .

В итоге имеем зависимость синусоидального тока от напряжения согласно Закону Ома,
где в знаменателе вместо R выражение ωL, которое и является реактивным сопротивлением:

Реактивное сопротивлениие индуктивностей называют индуктивным.

Описание устройства

Катушка индуктивности бывает винтовой, спиральной или винтоспиральной, имеющей свернутый изолированный проводник, который обладает значительным показателем индукции при малой емкости с активным сопротивлением. Как следствие, ток протекает через источник тока со значительной инерционностью.

Главный компонент электроцепи

Обратите внимание! Применяется, чтобы подавлять помехи, сглаживать биения, накапливать энергию, ограничивать переменный ток или резонансный/частотно-избирательный контур цепи. Стоит указать, что ее применение разнообразно

Называется она дросселем, вариометром, соленоидом и токоограничивающим реактором. При этом основные технические характеристики варьируются. Могут отличаться силой тока, сопротивлением потерь, добротностью, емкостью и температурным добротным коэффициентом

Стоит указать, что ее применение разнообразно. Называется она дросселем, вариометром, соленоидом и токоограничивающим реактором. При этом основные технические характеристики варьируются. Могут отличаться силой тока, сопротивлением потерь, добротностью, емкостью и температурным добротным коэффициентом.

Полное определение из физики

Похожие записи:

Установка дин рейки. монтаж электооборудования на din-рейке. что такое дин-рейка в электрике, согласно гост: особенности крепления счетчика и других приборов Повторное заземление вли Какие характеристики у датчика температуры и влажности ардуино? Проверка (прозвонка) светодиода мультиметром Диэлектрики: определения, формулы, примеры Делители напряжения емкостные электронные с цифровым выходом днеэ