Примечания
Математические детали общего понятия ориентации базиса, о котором здесь идёт речь — см. в статье Ориентация.
Под определением направления здесь везде имеется в виду выбор одного из двух противоположных направлений (выбор между всего двумя противоположными векторами), то есть сводится к выбору положительного направления.
Это означает, что другие правила могут быть также удобны в любом количестве, но их использование не является необходимым.
Это означает, что при желании можно пользоваться и противоположным правилом, и иногда это может быть даже удобно.
Понятие правого и левого базиса распространяются не только на ортонормированные, но на любые трехмерные базисы (то есть и на косоугольные декартовы координаты тоже), однако мы для простоты ограничимся здесь случаем ортонормированных базисов (прямоугольных декартовых координат с равным масштабом по осям).
Можно проверить, что в целом это действительно так, исходя из элементарного определения векторного произведения: Векторное произведение есть вектор, перпендикулярный обоим векторам-сомножителям, а по величине (длине) равный площади параллелограмма. То же, какой из двух возможных векторов, перпендикулярных двум заданным, выбрать — и есть предмет основного текста, правило, позволяющее это сделать и дополняющее приведённое здесь определение, указано там.
Левая резьба применяется в современной технике только тогда, когда применение правой резьбы привело бы к опасности самопроизвольного развинчивания под влиянием постоянного вращения данной детали в одном направлении — например, левая резьба применяется на левом конце оси велосипедного колеса
Помимо этого, левая резьба применяется в редукторах и баллонах для горючих газов, чтобы исключить подсоединение к кислородному баллону редуктора для горючего газа.
В том числе они могут быть в своих случаях и более удобными, чем общее правило, и даже иногда сформулированы достаточно органично, чтобы особенно легко запоминаться; что, правда, по-видимому, всё же не делает запоминание их всех более лёгким, чем запоминание всего одного общего правила.
Даже если мы имеем дело с достаточно асимметричным (и асимметрично расположенным относительно оси вращения) телом, так что коэффициентом пропорциональности между угловой скоростью и моментом импульса служит тензор инерции, несводимый к численному коэффициенту, и вектор момента импульса тогда вообще говоря не параллелен вектору угловой скорости, тем не менее правило работает в том смысле, что направление указывается приблизительно, но этого достаточно, чтобы сделать выбор между двумя противоположными направлениями.
Строго говоря, при этом сопоставлении есть ещё постоянный коэффициент 2, но в данной теме это не важно, так как речь идет сейчас только о направлении вектора, а не о его величине. Не обязательное требование.
Не обязательное требование.
Сила Ампера: варианты расчета
Прежде чем сформулировать данную величину, необходимо разобраться, что такое понятие сила в физике. Ей называется величина в физике, которая является мерой воздействия всех окружающих тел на рассматриваемый объект. Обычно любую силу обозначают английской буквой F, от латинского fortis, что означает сильный.
Рассчитывается элементарная сила Ампера по формуле:
где, dl – часть длины проводника, B –индукция магнитного контура, I – сила тока.
Рассчитывается также сила Ампера по формуле:
где, J – направление плотности тока, dv– элемент объема проводника.
Формулировка расчета модуля силы Ампера, согласно литературе, звучит так: данный показатель напрямую зависит от силы тока, протяженности проводника, синуса, образуемого между этим вектором и самим проводником угла, и величины значения вектора магнитного контура в модуле. Она и носит название модуля силы Ампера. Формула данного закона математически строится так:
где, B – модуль индукции магнитного контура, I – сила тока, l – длина проводника, α – образуемый угол. Максимальное значение будет при перпендикулярном их пересечении.
Показатель измеряется в ньютонах (условное обозначение – Н) или
. Он является векторной величиной и зависит от вектора индукции и тока.
Существуют и другие формулы для расчета силы Ампера. Но на практике они достаточно редко востребованы и тяжелы для понимания.
Условные обозначения
- Направление механической силы буквальное.
- Направление магнитного поля — с севера на юг.
- Направление электрического тока такое же, как у обычного тока : от положительного к отрицательному.
Первый вариант
- Большой палец представляет направление движения проводника.
- Указательный палец представляет направление магнитного поля.
- Центральный палец представляет направление Течения.
Второй вариант
- Чт м б представляет направление М otion в результате силы , действующей на проводник
- F рвый палец представляет направление магнитного F IELD
- Se с Зонд палец представляет направление C омер текущего.
Третий вариант
Перевод Ван де Граафа правил Флеминга — это правило ФБР, которое легко запомнить, потому что это инициалы Федерального бюро расследований .
Четвертый вариант (ФБР)
- F (Большой палец) представляет направление сил проводника
- Б (указательный) представляет направление магнитного поля
- I (Центр палец) представляет направление течения.
При этом используются обычные символические параметры F (для силы Лоренца ), B (для плотности магнитного потока ) и I (для электрического тока ), и они приписываются в этом порядке (FBI) соответственно большому, первому и второму пальцам.
- Большой палец — сила, F
- Первый палец — это плотность магнитного потока, B
- Второй палец — это электрический ток, I.
Конечно, если мнемоника преподается (и запоминается) с другим расположением параметров для пальцев, это может закончиться как мнемоника, которая также меняет роли двух рук (вместо стандартной левой руки для двигателей, правой рука для генераторов). Эти варианты более полно каталогизированы на странице мнемоники ФБР .
Пятый вариант (выстрелить в поле, почувствовать силу и убить течение)
Этот подход к запоминанию того, какой палец представляет, какое количество использует некоторые действия. Прежде всего, вам нужно указать пальцами, как на воображаемое ружье, причем указательный палец действует как ствол пистолета, а большой палец действует как курок. Затем выполните следующие действия:
- «Разожгите поле» указательным пальцем
- «Почувствуйте силу» отдачи оружия большим пальцем.
- Наконец, вы показываете средний палец, когда «убиваете ток».
Что такое сила Лоренца — определение, когда возникает, получение формулы
Известно, что электрический ток – это упорядоченное перемещение заряженных частиц. Установлено также, что во время движения в магнитном поле каждая из этих частиц подвергается действию силы. Для возникновении силы требуется, чтобы частица находилась в движении.
Сила Лоренца – это сила, которая действует на электрически заряженную частицу при её движении в магнитном поле. Её направление ортогонально плоскости, в которой лежат векторы скорости частицы и напряженности магнитного поля. Равнодействующая сил Лоренца и есть сила Ампера. Зная ее, можно вывести формулу для силы Лоренца.
Время, требуемое для прохождения частицей отрезка проводника, , где – длина отрезка, – скорость частицы. Суммарный заряд, перенесенный за это время через поперечное сечение проводника, . Подставив сюда значение времени из предыдущего равенства, имеем
(2)
В то же время , где – количество частиц, находящееся в рассматриваемом проводнике. При этом , где – заряд одной частицы. Подставив в формулу значение из (2), можно получить:
Таким образом,
Используя (1), предыдущее выражение можно записать как
После сокращений и переносов появляется формула для вычисления силы Лоренца
С учетом того, что формула записана для модуля силы, ее необходимо записать так:
(3)
Поскольку , то для вычисления модуля силы Лоренца неважно, куда направлена скорость, – по направлению силы тока или против, – и можно сказать, что – это угол, образуемый векторами скорости частицы и магнитной индукции. Запись формулы в векторном виде будет выглядеть следующим образом:
Запись формулы в векторном виде будет выглядеть следующим образом:
– это векторное произведение, результатом которого является вектор с модулем, равным .
Исходя из формулы (3), можно сделать вывод о том, что сила Лоренца является максимальной в случае перпендикулярности направлений электрического тока и магнитного поля, то есть при , и исчезать при их параллельности ().
Необходимо помнить, что для получения правильного количественного ответа – например, при решении задач, – следует пользоваться единицами системы СИ, в которой магнитная индукция измеряется в теслах (1 Тл = 1 кг·с−2·А−1), сила – в ньютонах (1 Н = 1 кг·м/с2), сила тока – в амперах, заряд в кулонах (1 Кл = 1 А·с), длина – в метрах, скорость – в м/с.
Физическая основа правил
Прогнозирование направления плотности потока ( B ), учитывая, что ток I течет в направлении большого пальца.
Когда электроны или любые заряженные частицы текут в одном и том же направлении (например, как электрический ток в электрическом проводнике , таком как металлический провод ), они создают цилиндрическое магнитное поле , охватывающее проводник (как обнаружил Ганс Кристиан Эрстед. ).
Направление индуцированного магнитного поля можно запомнить по правилу штопора Максвелла . То есть, если обычный ток течет от наблюдателя, магнитное поле движется по часовой стрелке вокруг проводника в том же направлении, в котором штопор должен был бы повернуться, чтобы уйти от наблюдателя. Направление индуцированного магнитного поля также иногда запоминается правилом для правой руки , как показано на иллюстрации, с большим пальцем, показывающим направление обычного тока, и пальцами, показывающими направление магнитного поля. Существование этого магнитного поля может быть подтверждено размещением магнитных компасов в различных точках по периферии электрического проводника, по которому проходит относительно большой электрический ток.
Большой палец показывает направление движения, указательный палец показывает линии поля, а средний палец показывает направление индуцированного тока.
Если внешнее магнитное поле приложено горизонтально, так что оно пересекает поток электронов (в проводнике или в электронном пучке), два магнитных поля будут взаимодействовать. Майкл Фарадей представил для этого визуальную аналогию в виде воображаемых магнитных силовых линий : те, что в проводнике, образуют концентрические круги вокруг проводника; те, которые находятся во внешнем магнитном поле, идут параллельными линиями. Если те, которые находятся на одной стороне проводника, движутся (от северного магнитного полюса к южному) в направлении, противоположном тем, которые окружают проводник, они будут отклонены так, что они пройдут с другой стороны проводника (потому что магнитные силовые линии не могут пересекаются или бегут друг против друга). Следовательно, будет большое количество силовых линий магнитного поля в небольшом пространстве на этой стороне проводника и их недостаток на исходной стороне проводника. Поскольку силовые линии магнитного поля больше не являются прямыми линиями, а изогнуты, чтобы проходить вокруг электрического проводника, они находятся под напряжением (как растянутые эластичные ленты), а энергия связана в магнитном поле. Так как это энергетическое поле сейчас в основном не встречает сопротивления, его наращивание или вытеснение в одном направлении создает — аналогично третьему закону движения Ньютона — силу в противоположном направлении. Поскольку в этой системе есть только один подвижный объект (электрический проводник), на который действует эта сила, результирующий эффект представляет собой физическую силу, работающую, чтобы вытеснить электрический проводник из внешнего магнитного поля в направлении, противоположном тому, на которое магнитный поток перенаправляется на — в этом случае (двигатели), если проводник проводит обычный ток вверх , а внешнее магнитное поле перемещается от наблюдателя, физическая сила будет толкать проводник влево . Это причина крутящего момента в электродвигателе. (Электродвигатель затем сконструирован так, что выталкивание проводника из магнитного поля заставляет его помещаться в следующее магнитное поле, и это переключение продолжается бесконечно.)
Закон Фарадея : индуцированная электродвижущая сила в проводнике прямо пропорциональна скорости изменения магнитного потока в проводнике.
Какое правило применить
Слова синонимы: рука, винт, буравчик
Вначале разберем слова-синонимы, многие начали спрашивать себя: если тут повествование должно затрагивать буравчик, почему текст постоянно касается рук. Введем понятие правой тройки, правой системы координат. Итого, 5 слов-синонимов.
Потребовалось выяснить векторное произведение векторов, оказалось: в школе это не проходят. Проясним ситуацию любознательным школьникам.
Декартова система координат
Школьные графики на доске рисуют в декартовой системе координат Х-Y. Горизонтальная ось (положительная часть) направлена вправо – надеемся, вертикальная – указывает вверх. Делаем один шаг, получая правую тройку. Представьте: из начала отсчета в класс смотрит ось Z. Теперь школьники знают определение правой тройки векторов.
В Википедии написано: допустимо брать левые тройки, правые, вычисляя векторное произведение, несогласны. Усманов в этом плане категоричен. С разрешения Александра Евгеньевича приведем точное определение: векторным произведением векторов называют вектор, удовлетворяющий трем условиям:
- Модуль произведения равен произведению модулей исходных векторов на синус угла меж ними.
- Вектор результата перпендикулярен исходным (вдвоем образуют плоскость).
- Тройка векторов (по порядку упоминания контекстом) правая.
Правую тройку знаем. Итак, если ось Х – первый вектор, Y – второй, Z будет результатом. Почему назвали правой тройкой? По-видимому, связано с винтами, буравчиками. Если закручивать воображаемый буравчик по кратчайшей траектории первый вектор-второй вектор, поступательное движение оси режущего инструмента станет происходить в направлении результирующего вектора:
- Правило буравчика применяется к произведению двух векторов.
- Правило буравчика качественно указывает направление результирующего вектора этого действия. Количественно длина находится выражением, упомянутым (произведение модулей векторов на синус угла меж ними).
Простые приемы запоминания правил буравчика
Люди забывают, что силу Лоренца проще определять правилом буравчика с левосторонней резьбой. Желающий понять принцип действия электрического двигателя должен как дважды два щелкать подобные орешки. В зависимости от конструкции число катушек ротора бывает значительным, либо схема вырождается, становясь беличьей клеткой. Ищущим знания помогает правило Лоренца, описывающее магнитное поле, где движутся медные проводники.
Для запоминания представим физику процесса. Допустим, движется электрон в поле. Применяется правило правой руки для нахождения направления действия силы. Доказано: частица несет отрицательный заряд. Направление действия силы на проводник находится правилом левой руки, вспоминаем: физики совершенно с левых ресурсов взяли, что электрический ток течет в направлении противоположном тому, куда направились электроны. И это неправильно. Поэтому приходится применять правило левой руки.
Не всегда следует идти такими дебрями. Казалось бы, правила больше запутывают, не совсем так. Правило правой руки часто применяется для вычисления угловой скорости, которая является геометрическим произведением ускорения на радиус: V = ω х r. Многим поможет визуальная память:
- Вектор радиуса круговой траектории направлен из центра к окружности.
- Если вектор ускорения направлен вверх, тело движется против часовой стрелки.
https://youtube.com/watch?v=enwbrdUcbvU
Посмотрите, здесь опять действует правило правой руки: если расположить ладонь так, чтобы вектор ускорения входил перпендикулярно в ладонь, персты вытянуть по направлению радиуса, отогнутый на 90 градусов большой палец укажет направление движения объекта. Достаточно однажды нарисовать на бумаге, запомнив минимум на половину жизни. Картинка действительно простая. Больше на уроке физики не придется ломать голову над простым вопросом – направление вектора углового ускорения.
Аналогичным образом определяется момент силы. Исходит перпендикулярно из оси плеча, совпадает направлением с угловым ускорением на рисунке, описанном выше. Многие спросят: зачем нужно? Почему момент силы не скалярная величина? Зачем направление? В сложных системах непросто проследить взаимодействия. Если много осей, сил, помогает векторное сложение моментов. Можно значительно упростить вычисления.
Применение в жизни
В электротехнике закон Ампера «играет» одну из самых важных «ролей». Давайте обсудим случаи его применения на практике. Электропривод — это основа практически каждого предприятия. Для передвижения или доведения до действий всевозможных систем, таких как:
- электромобили;
- трамваи;
- троллейбусы;
- автоматизированные задвижки трубопроводов;
- грузоподъемных механизмов;
- электротранспорта (электровозы на ЖД) и других,
применяются двигатели и электромагнитные исполнительные механизмы.
В результате содействия между обмотками ротора и статора, сила вынуждает двигатель вращаться.
https://youtube.com/watch?v=SLT6hftSXuM
Чтобы заставить обмотки вращаться, их либо переключают с помощью щеточного узла и коллектора в двигателях постоянного тока, либо используют переменный ток.
Ее действие просматривается при коротких замыканиях на линиях электропередач. Там, под влиянием сверхбольших токов, провода и шины начинают изгибаться.
В рельсотроне в момент выстрела раздвигаются рельсы. Это предопределено уже вышеперечисленными причинами.
Правило левой руки
Рассмотрим правило: если разместить левую ладошку так, что четыре остальные пальца показывают направленность тока, то в этом случае линии индукции будут поступать в ладошку под прямым углом, а отвёрнутый заглавный палец и покажет вектор существующей силы.
Имеется иное обозначение. Направленность силы Ампера и силы Лоренца должен указывать выставленный главный палец левой руки в том случае, если оставшиеся четыре пальца будут размещены в сторону передвижения положительно и отрицательно заряженных элементов электрического тока, и линии индукции образованного поля будут вертикально входить в ладошку. Это изобретение считается теоретическим и практическим объяснением способа работы двигателей и генераторов, работающих с помощью электрического тока.
Можно сделать вывод, что знание данных правил и умение их использовать на практике, позволяют создавать и придумывать электрические приборы и успешно работать с ними.
https://youtube.com/watch?v=DLWUlN9MxRA
Обнаружение МП по его действию на эл. ток. Правило левой руки
Поскольку магнитное поле проводника с током действует с определённой силой на магнит, то естественно предположить, что со стороны магнитного поля магнита на проводник с током также должна действовать какая-то сила. Рассмотрим более подробно действие магнитного поля на проводник с током и попытаемся подтвердить или опровергнуть высказанное предположение.
Для этого соберём цепь, состоящую из источника тока, ключа, трёхсторонней рамки, реостата и подковообразного магнита, закреплённого в штативе. Рамку подвесим на крючках так, чтобы она могла свободно вращаться, и поместим в магнитное поле, созданное подковообразным магнитом. Присоединим рамку к источнику тока, последовательно с реостатом и ключом. При разомкнутой цепи действия со стороны магнитного поля магнита на рамку не наблюдается. Если же цепь замкнуть, то проводник приходит в движение — он втягивается в пространство между полюсами дугообразного магнита.
Следовательно, магнитное поле действует на рамку с током с некоторой силой
, отклоняющей её от первоначального положения.
Раз магнитное поле способно оказывать действие на проводник с током, то это действие может быть использовано для обнаружения магнитного поля в данной области пространства.
Кто-то из вас скажет, что зачем столько сложностей, если магнитное поле можно обнаружить с помощью простого компаса.
Да, с помощью компаса проще, но вспомните гипотезу Ампера: внутри каждой молекулы вещества циркулируют кольцевые электрические токи.
Поэтому действие магнитного поля на стрелку компаса сводится к действию поля на элементарные электрические токи, которые циркулируют в атомах и молекулах вещества, из которого изготовлена магнитная стрелка.
Таким образом, магнитное поле создаётся электрическим током и обнаруживается по его действию на электрический ток.
Но вернёмся к нашему опыту. Давайте поменяем направление тока в цепи. Замкнув её увидим, что проводник отклонился в противоположную сторону.
Значит, вместе с током изменилось и направление действующей на рамку силы.
Если теперь поменять местами полюсы магнита (то есть изменить направление магнитных линий), то мы увидим, как рамка с током вновь втягивается в пространство между полюсами магнита.
Значит, направление тока в проводнике, направление линий магнитного поля и направление силы, действующей на проводник с током, связаны между собой.
Из курса физики восьмого класса вы знаете, что сила, с которой магнитное поле действует на помещённый в него проводник с током, называется силой Ампера,
в честь французского учёного Андре-Мари Ампера.
Направление силы Ампера можно определить с помощью правила левой руки: если левую руку расположить так, чтобы линии магнитного поля входили в ладонь, а четыре пальца были направлены по направлению тока в проводнике, то отогнутый на девяносто градусов большой палец покажет направление действующей на проводник силы.
При использовании данного правила не забывайте о том, что за направление тока в цепи принято направление в котором движутся или могли бы двигаться положительно заряженные частицы.
С помощью правила левой руки также определяют и направление силы, действующую на отдельную заряженную частицу, движущуюся в магнитном поле. Для самого простого случая, то есть когда частица движется перпендикулярно линиям магнитного поля, это правило звучит так: если левую руку расположить так, чтобы линии магнитного поля входили в ладонь перпендикулярно к ней, а четыре пальца были направлены по движению положительно заряженной частицы (или против движения отрицательно заряженной), то отставленный на девяносто градусов большой палец покажет направление действующей на частицу силы.
Обратим внимание ещё на один важный момент: магнитное поле не действует в случаях, если прямолинейный проводник с током или скорость движущейся заряженной частицы параллельны линиям магнитного поля или совпадают с ними
Немного истории
Первые попытки описать электромагнитную силу были сделаны еще в XVIII веке. Ученые Генри Кавендиш и Тобиас Майер высказали предположение, что сила на магнитных полюсах и электрически заряженных объектах подчиняется закону обратных квадратов. Однако экспериментальное доказательство этого факта не было полным и убедительным. Только в 1784 году Шарль Августин де Кулон при помощи своего торсионного баланса смог окончательно доказать это предположение.
В 1820 году физиком Эрстедом был открыт факт, что на магнитную стрелку компаса действует ток вольта, а Андре-Мари Ампер в этом же году смог разработать формулу угловой зависимости между двумя токовыми элементами. По сути, эти открытия стали фундаментом современной концепции электрических и магнитных полей. Сама же концепция получила свое дальнейшее развитие в теориях Майкла Фарадея, особенно в его представлении о силовых линиях. Лорд Кельвин и Джеймс Максвелл дополнили теории Фарадея подробным математическим описанием. В частности Максвеллом было создано так званное, «уравнение поля Максвелла» – представляющее собой систему дифференциальных и интегральных уравнений, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах.
Джей Джей Томпсон был первым физиком, кто попытался вывести из уравнения поля Максвелла электромагнитную силу, которые действует на движущийся заряженный объект. В 1881 году он опубликовал свою формулу F = q/2 v x B. Но из-за некоторых просчетов и неполного описания тока смещения она оказалась не совсем правильной.
И вот, наконец, в 1895 году голландский ученый Хендрик Лоренц вывел правильную формулу, которая используется и поныне, а также носит его имя, как и та сила, что действует на летящую частицу в магнитном поле, отныне называется «силой Лоренца».
Хендрик Лоренц.
Понятие вектора
Полагаем, нет смысла истолковывать правило буравчика при отсутствии знания определения вектора. Требуется открыть бутылку – знание о правильных действиях поможет. Вектором называют математическую абстракцию, не существующую реально, выказывающую указанные признаки:
- Направленный отрезок, обозначаемый стрелкой.
- Точкой начала послужит точка действия силы, описываемой вектором.
- Длина вектора равна модулю силы, поля, прочих описываемых величин.
Не всегда затрагивают силу. Векторами описывается поле. Простейший пример показывают школьникам преподаватели физики. Подразумеваем линии напряженности магнитного поля. Вдоль обычно рисуются векторы по касательной. В иллюстрациях действия на проводник с током увидите прямые линии.
Правило буравчика
Векторные величины часто лишены места приложения, центры действия выбираются по договоренности. Момент силы исходит из оси плеча. Требуется для упрощения сложения. Допустим, на рычаги различной длины действуют неодинаковые силы, приложенные к плечам с общей осью. Простым сложением, вычитанием моментов найдем результат.
Векторы помогают решить многие обыденные задачи и, хотя выступают математическими абстракциями, действуют реально. На основе ряда закономерностей возможно вести предсказание будущего поведения объекта наравне со скалярными величинами: поголовье популяции, температура окружающей среды. Экологов интересуют направления, скорость перелета птиц. Перемещение является векторной величиной.
Правило буравчика помогает найти векторное произведение векторов. Это не тавтология. Просто результатом действия окажется тоже вектор. Правило буравчика описывает направление, куда станет указывать стрелка. Что касается модуля, нужно применять формулы. Правило буравчика – упрощенная чисто качественная абстракция сложной математической операции.
Взаимодействие токов
Рассмотрим два случая. Первый – ток течет по прямому проводу. Второй – по круговому витку. Как мы знаем, ток создает магнитное поле.
В первом случае магнитная индукция провода с током I на расстоянии R от него считается по формуле:
Мю – магнитная проницаемость вещества, мю с индексом ноль – магнитная постоянная.
Во втором случае магнитная индукция в центре кругового витка с током равна:
Также при решении задач может пригодиться формула для магнитного поля внутри соленоида. Соленоид – это катушка, то есть множество круговых витков с током.
Пусть их количество – N, а длина самого соленоилда – l. Тогда поле внутри соленоида вычисляется по формуле:
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Применение правила буравчика
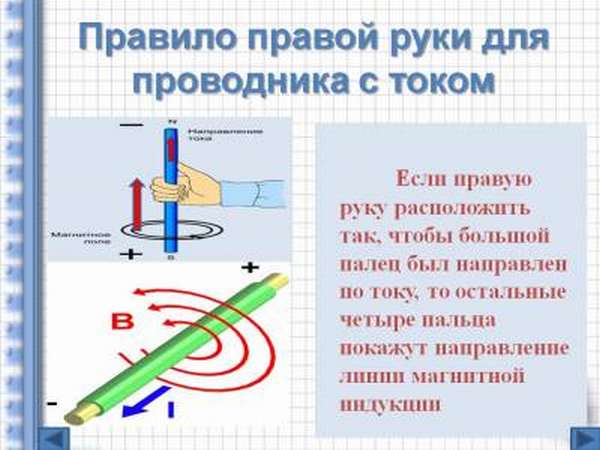Данное правило гласит: если при движении вперед этого устройства траектория движения тока в проводнике совпадает с ним, то траектория вращения основания прибора комплементарна траектории движения магнитного контура.
Чтобы определить траекторию вращения магнитного контура на представленном графическом изображении нужно знать несколько особенностей.
Часто в задачах по физике нужно, наоборот, определить траекторию движения тока. Чтобы это сделать, дается направление вращения кругов магнитного поля. Ручка буравчика начинается вращаться в сторону, указанную в условиях. Если буравчик движется в поступательном направлении, значит, ток направлен в сторону движения, если же он направлен в обратную, то и ток движется соответственно.
Для определения траектории движения тока в случае, представленном на втором рисунке, тоже можно воспользоваться правилом штопора. Для этого необходимо вращать ручку буравчика в сторону, указанную на изображении контура магнитного поля. Если он будет двигаться поступательно, то ток будет двигаться в сторону от наблюдателя, если же, наоборот, только к наблюдателю.
Важно! Если указана траектория движения потока, то определить траекторию вращения линии магнитного контура можно по вращению ручки буравчика
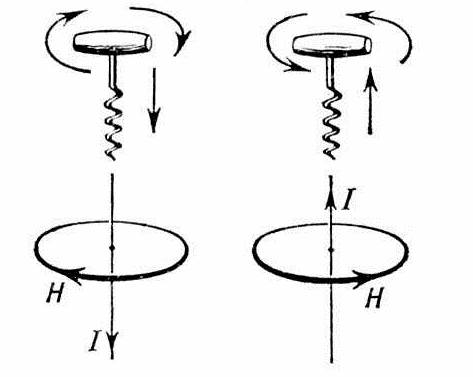
Оно обозначается при помощи точки или крестика. Точка означает движение в сторону наблюдателя, крестик означает обратное. Легко запомнить этот случай, используя так называемое правило «стрелы», если острие «смотрит», а в лицо, то траектория движения тока в сторону наблюдателя, если же в лицо «смотрит хвост стрелы», то она двигается от наблюдателя.
Как правило буравчика, так и правило правой руки, достаточно легко применить на практике. Для этого нужно расположить кисть соответствующей руки таким образом, чтобы в лицевую сторону направлялся силовой контур магнитного поля, после чего большой палец, отведенный перпендикулярно, необходимо направить сторону движения тока, соответственно, остальные выпрямленные пальцы укажут на траекторию магнитного контура.
Различают исключительные случаи использования правила правой руки для вычисления:
- уравнения Максвелла,
- момента силы,
- угловой скорости,
- момента импульса,
- магнитной индукции,
- тока в проводе, движущегося через магнитное поле.
