2 закон Кирхгофа
При расчете электрических цепей в большинстве случаев нам встречаются цепи, образующие замкнутые контуры. В состав таких контуров, кроме сопротивлений, могут входить ЭДС (источники напряжений). На рисунке 4 представлен участок такой электрической цепи. Произвольно выбираем положительные направления токов. Обходим контур от точки А в произвольном направлении (выберем по часовой стрелке). Рассмотрим участок АБ: происходит падение потенциала (ток идет от точки с высшим потенциалом к точке с низшим потенциалом).
- На участке АБ: φА + E1 – I1r1 = φБ.
- БВ: φБ – E2 – I2r2 = φВ.
- ВГ: φВ – I3r3 + E3 = φГ.
- ГА: φГ – I4r4 = φА.
- Складывая данные уравнения, получим: φА + E1 – I1r1 + φБ – E2 – I2r2 + φВ – I3r3 + E3 + φГ – I4r4 = φБ + φВ + φГ + φА
- или: E1 – I1r1 – E2 – I2r2 – I3r3 + E3 – I4r4 = 0.
- Откуда имеем следующее: E1 – E2 + E3 = I1r1 + I2 r2 + I3r3 + I4r4.
Таким образом, получаем формулу второго закона Кирхгофа в комплексной форме:
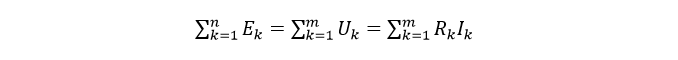
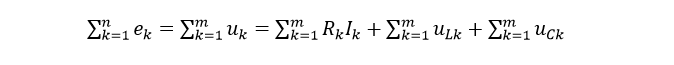
Теперь можем сформулировать определение 2 (второго) закона Кирхгофа:
Второй закон Кирхгофа гласит, что алгебраическая сумма напряжений на резистивных элементах замкнутого контура, равна алгебраической сумме ЭДС, входящих в этот контур. В случае отсутствия источников ЭДС, суммарное напряжение равно нулю.
Иначе формулируя второе правило Кирхгофа, можно сказать: при полном обходе контура потенциал, изменяясь, возвращается к начальному значению.
При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура, при этом падение напряжения на ветви считается положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, в противном случае – отрицательным.
Определить знак можно по алгоритму:
- 1. выбираем направление обхода контура (по или против часовой стрелки);
- 2. произвольно выбираем направления токов через элементы цепи;
- 3. расставляем знаки для напряжений и ЭДС по правилам (ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура со знаком «+», иначе – «-»; напряжения, падающие на элементах цепи, если ток, протекающий через эти элементы совпадает по направлению с обходом контура, со знаком «+», в противном случае – «-»).
Закон Ома является частным случаем второго правила для цепи.
Приведем пример применения второго правила Кирхгофа:
По данной электрической цепи (Рис 6) необходимо найти ее ток. Произвольно берем положительное направление тока. Выберем направление обхода по часовой стрелке, запишем уравнение 2 закона Кирхгофа:
Знак минус означает, что выбранное нами направление тока противоположно его действительному направлению.
Решение задач
1. По приведенной схеме записать законы Кирхгофа для цепи.
| Дано: | Решение: |
|---|---|
|
|
2. На рисунке приведена цепь с двумя источниками ЭДС величиной 12 В и 5 В, с внутренним сопротивлением источников 0,1 Ом, работающих на общую нагрузку 2 ома. Как будут распределены токи в этой цепи, какие они имеют значения?.
Формулировка правил
Каждое правило Кирхгофа обладает универсальными свойствами. Как первое, так и второе, хоть и не относятся к фундаментальным законам, но твёрдо обоснованы.
Определения
Прежде, чем рассматривать простые принципы и смысл решения СУ (систем уравнений), нужно определиться с применяемыми формулировками. В типологии цепей пользуются следующими понятиями:
- ветвь;
- узел;
- контур.
Всё это – элементы электрической цепи (ЭЦ).
Элементы ЭЦ
Часть электроцепи, через которую проходит электричество одной и той же величины, называется ветвью. Место, в котором соединяются три и более ветви, именуют узлом. Обычно на схемах узлы обозначаются крупными точками. Контуром называется путь, по которому протекает электрический ток, проходя через несколько участков ЭЦ, включающих в себя узлы и ветви.
Важно! Ток (I), выходя из одной точки контура и единожды проходя по разветвлениям и узлам, должен обязательно вернуться в начало. Контур – это замкнутая цепь
Узлы и ветви, подлежащие изучаемому в определённый момент контуру, могут входить в состав других контуров: являться общими для нескольких замкнутых ЭЦ одновременно.
Первое правило
Первая закономерность Кирхгофа звучит так: «Сумма всех токов в узлах ЭЦ равна нулю». Если придать направление токам, текущим сквозь пересечения проводников, имеющих общий контакт (узел), то можно промаркировать стрелками, указывающими на узел, втекающие токи. Стрелками, имеющими направленность от узла, удобно отмечать вытекающие токи:
I1 + I2 – I3 – I4 – I5 = 0
Изображение направления движения электричества
Условно считая, что входящие I имеют плюсовой знак, а выходящие – минусовой, можно перефразировать утверждение. Согласно закону сохранения заряда, алгебраические суммы входящих в узел и выходящих из него I по значению равны.
Первый закон
Убедиться в истинности первого правила можно, собрав смешанную схему включения резисторов, в качестве нагрузки, для источника питания U = 3 В.
Включенные в ветви амперметры позволяют визуально зафиксировать значения токов, входящих и выходящих из первого узла. Их алгебраическая сумма (учитывая знаки) будет равна нулю.
Схема цепи с установкой амперметров
Второе правило
Его называют правилом напряжений, оно утверждает, что сумма всех E (ЭДС), входящих в контур, равняется сумме падений напряжений на резистивных элементах, при условии, что контур замкнутый:
ΣE = ΣI*R.
Например, для цепи с элементом питания и резистором напряжение на резисторе U = I*R будет равно ЭДС батарейки. По второму определению Кирхгофа выражение будет иметь вид:
E = I*R.
Схема с одной ЭДС и одним резистором
По аналогии, если количество резисторов увеличить, то падение напряжения на них распределится так, что в сумме они сравняются со значением ЭДС источника питания:
E = I*R1 + I*R2 + I*R.
Включение одной ЭДС и трёх резисторов одного номинала
Объяснение было бы не полным, если не рассмотреть схему с несколькими ЭДС, входящими в контур. В этом случае выражать равенство следует следующим образом:
E1 + E2 = I*R1 + I*R2 + I*R3.
К сведению. При подключении нескольких источников в один контур необходимо соблюдать полярность, выполняя последовательное соединение плюса одного источника с минусом другого, таким образом, значения ЭДС будут суммироваться.
Включение двух источников в контур
https://youtube.com/watch?v=6r4Y318cGhA
Примеры решения задач
| Задание | Как следует записать уравнение для токов, используя первое правило Кирхгофа для узла А, изображенного на рис.1 |
Решение
Прежде чем применять первое правило Кирхгофа определим для себя, что положительными будут токи, которые входят в узел А, тогда выходящие из этого узла токи мы должны будем записать в первом правиле Кирхгофа со знаком минус. Из рис. 1 в узел А входят токи:
Из узла А выходят токи:
Тогда согласно правилу узлов имеем:
Ответ
| Задание | Составьте систему независимых уравнений, используя правила Кирхгофа, которая позволит найти все токи в цепи, представленной на рис.2, если известны все ЭДС и все сопротивления (они указаны на рисунке)? |
Решение
Направления токов выберем произвольно, обозначим их на рис.1. Пусть через сопротивление течет ток . На рис.2 видно, что в нашей цепи два узла. Это точки A и С. Запишем первое правило Кирхгофа для узла А:
Так как узлов всего два, то первое правило Кирхгофа даст нам только одно независимое уравнение (2.1).
Контуров в подставленной цепи три. Втрое правило Кирхгофа даст нам два независимых уравнения. Рассмотрим контуры ABCA и ACDA. Направлением обхода выберем движение против часовой стрелки. Тогда для контура ABCA имеем:
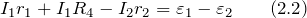
Для контура ACDA получим:
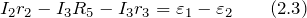
Получили систему из трех независимых уравнений для трех неизвестных токов:
Густав-Роберт Киргоф, выдающийся немецкий физик и математик позапрошлого века, открыл и сформулировал два электротехнических закона, названных в его честь.
Открытия Кирхгоффа
При всей видимой простоте и понятности, законы Кирхгофа стали фундаментальными основами современной науки и базой для методов схематических расчетов. Их практическое значение трудно переоценить. Базой для научных изысканий профессора Кирхгофа стали законы сохранения заряда и энергии, открытые ранее. Некоторые специалисты считают, что правильнее называть описанные Кирхгоффом закономерности правилами, чтобы не путать их с другими замечательными открытиями этого физика, касающимися способностей тел излучать и поглощать энергию, а также зависимости скорости протекания химических реакций от температуры. Однако в научной и технической литературе принято все же пользоваться термином «закон Кирхгофа», тем самым подчеркивая заслуги этого великого ученого в области электротехники. Итак, их два.
1. Закон Кирхгофа о токах в узлах
Узлами в электротехнике называют точки соединения проводников в количестве не менее трех. Для того чтобы понять действие Первого закона Киргофа, достаточно представить себе обычный водопроводный тройник. Если в одну из труб подается вода, то в две остальные она вытекает. Возможен и другой вариант, когда отводная труба одна, а приточных две, но в любом случае, сколько воды в тройник затечет, столько же и вытечет. Теперь задачу можно усложнить, допустив, что количество входов и выходов в узле сколь угодно большое. Однако результат будет тот же, количество поступающей и уходящей жидкости будет равным, то есть, говоря языком математики, алгебраическая сумма расходов равна нулю. Первый закон Кирхгофа рассматривает электрические токи в узлах, которые ведут себя так же, как и вода в тройнике. Если есть входящие и выходящие токи, то их сумма с учетом знака будет нулевой. При этом величина входящих токов обозначается положительным знаком «плюс», а выходящих – отрицательным «минус». Математическая формула выглядит примерно так:
где I вх. — величины входящих токов со знаком «+»;
I вых. — величины выходящих токов со знаком «-».
2. Закон Кирхгофа о сумме падений напряжений
Второй закон Кирхгофа понять несколько сложнее, у него нет столь прямых и наглядных ассоциаций как у первого, тем не менее, он тоже несложен. Для начала следует представить себе замкнутую простейшую электрическую цепь, состоящую из источника питания и активной нагрузки в виде сопротивления. При замыкании клемм выключателя через резистор пойдет ток, и все подаваемое напряжение на нем же упадет. Задача вновь усложняется, и количество сопротивлений изменяется. Теперь их много, и у всех разная величина. При прохождении через них электрического тока он будет в цепи одинаковым и, согласно закону Ома, равен напряжению источника, поделенному на сумму всех сопротивлений. На каждом из них будет падать его часть. Так вот, Второй закон Кирхгофа гласит, что общая сумма падений напряжений на каждом из участков цепи равна величине напряжения питания. Говоря иными словами, общая алгебраическая сумма вместе с источником равна нулю.
Простейшая математическая формула описывает Второй закон Кирхгофа следующим образом:
где U ц – падения напряжений на разных участках замкнутой электрической цепи (контура).
§ 15. Второй закон Кирхгофа. Применение законов Кирхгофа для расчета электрических цепей
При расчете электрических цепей часто приходится встречаться с цепями, которые образуют замкнутые контуры. В состав таких контуров, помимо сопротивлений, могут входить еще электродвижущие силы.
На рис. 35 представлена часть сложной электрической цепи в виде замкнутого контура АБВГ. На схеме указаны полярность электродвижущих сил E1, E2, E3 и направления токов I1, I2, I3 и I4, протекающих на различных участках цепи.
Рис. 35. Участок сложной электрической цепи
Обходим контур от точки А в произвольном направлении, например по часовой стрелке. Рассмотрим каждый из участков рассматриваемого контура. На первом участке разность потенциалов между точками А и Б, или, что то же самое, напряжение UAБ, равна э.д.с. Е1 минус падение напряжения I1r1. Аналогично будет и на других участках цепи:
на участке АБ φА - φБ = Е1 - I1r1; на участке БВ φБ - φВ = -Е2 - I2r2; на участке ВГ φВ - φГ = E3 - I3r3; на участке ГА φГ - φА = I4r4.
Складывая левые и правые части уравнения, получим:
φA — φБ + φБ — φВ + φВ — φГ + φГ — φА = E1 — I1r1 — E2 — I2r2 + E3 I3r3 + I4r4;
0 = E1 — I1r1 — E2 — I2r2 + E3 — I3r3 + I4r4.
Перенося произведения (I⋅r) в одну часть, а электродвижущие силы (Е) в другую часть, получим
-E1 + E2 — E3 = — I1r1 — I2r2 — I3r3 + I4r4.
Или в общем виде
ΣE = ∑I ⋅ r.
Это выражение представляет собой второй закон Кирхгофа. Формула показывает, что во всяком замкнутом контуре алгебраическая сумма электродвижущих сил равна алгебраической сумме падений напряжений.
По второму закону Кирхгофа,
∑E = ∑Ir.
Для простейшей замкнутой цепи с одной э.д.с. Е (рис. 36)
E = Ir + Ir = I(r + r),
откуда
I = E/r+r.
Рис. 36. Простой замкнутый контур
Мы получили формулу закона Ома для замкнутой цепи.
Следовательно, закон Ома является частным случаем 2-го закона Кирхгофа.
При расчете электрических цепей применяют различные методы расчета. Выбор того или иного метода зависит от конфигурации цепи, числа э.д.с., заданных величин.
Как правило, расчет неразветвленных цепей с любым числом э.д.с., а также расчет сложных цепей с одной э.д.с. легче производить, применяя закон Ома.
Расчет сложных цепей с несколькими э.д.с. производят с помощью уравнений 1-го и 2-го законов Кирхгофа.
Расчет сложной цепи методом законов Кирхгофа производят в следующем порядке:
Условно задаются направлениями токов в различных участках цепи.
Определяют число уравнений, которое необходимо составить для решения задачи. Если известны все э.д.с. и сопротивления цепи, число уравнений должно быть равно числу неизвестных токов.
Для составления уравнений вначале используют уравнения 1-го закона Кирхгофа. Число уравнений 1-го закона Кирхгофа на единицу меньше числа узловых точек в схеме. Остальное число уравнений составляют по 2-му закону Кирхгофа.
Для этого намечают контуры, направление обхода этих контуров и приступают к составлению уравнений. Если направление обхода не совпадает с направлениями э.д.с. или с направлениями токов на отдельных участках контура, то величины э.д.с. и падения напряжения I⋅r входят в уравнения со знаком минус.
Решая систему уравнений, находят величину токов,
Если окажется, что в результате решения уравнений некоторые из токов получились отрицательными, то это значит, что направление этих токов было выбрано неправильно. Надо изменить направление токов на схеме.
Проверка правильности решения производится путем подстановки полученных значений токов в одно из составленных уравнений.
Решим несколько задач, используя закон Ома и оба закона Кирхгофа.
Пример 30. Найти токи в цепи, представленной на рис. 37. Выберем произвольно положительное направление тока. Обходя контур по часовой стрелке, пишем уравнение второго закона Кирхгофа:
-E1 + E2 = Ir1 + Ir2;
-1,9 + 1,3 = I(2 + 3);
-0,6 = 5I, I = -0,12 а.
Рис. 37. Электрическая цепь (к примеру 30)
Знак минус означает, что выбранное нами направление тока противоположно его действительному направлению.
Пример 31. Дана электрическая цепь (рис. 38). Определить токи на отдельных участках.
Рис. 38. Электрическая цепь (к примеру 31)
Произвольно выбираем положительные направления токов.
Для контура абде
6 = 2I1 + 5I3. (1)
Для контура авге
6 — 2 = 2I1 — 4I2. (2)
Для точки б, по первому закону Кирхгофа,
I3 = I1 + I2. (3)
Имеем три уравнения с тремя неизвестными. Решая их, находим величину и направление токов. Подставляя значение тока I3 из уравнения (3) в уравнение (1), получим
6 = 2I1 + 5I1 + 5I2; 6 = 7I1 + 5I2 + 2 = I1 - 2I2
или
12 = 14I1 + 10I2 + 10 = 5I1 + 10I2.
Складывая два последних уравнения, имеем:
22 = 19I1, откуда I1 = 1,156 а,
подставляем значение I1 в уравнение (1):
6 = 2 ⋅ 1,156 + 5I3,
| I3 = | 6 — 2 ⋅ 1,156 | = 0,74 а. |
| 5 |
Подставляем значение I1 в уравнение (2):
2 = 1,156 — 2I2,
откуда
| I2 = | — 2 + 1,156 | = — 0,422 a. |
| 2 |
Знак минус показывает, что действительное направление тока I2 обратно принятому нами направлению.
Законы Кирхгофа для расчёта электрических цепей
В цепях, состоящих из последовательно соединенных источника и приемника энергии, соотношения между током, сопротивлением и ЭДС всей цепи или на каком-либо участке цепи определяются законом Ома. Но на практике в цепях токи от какой-либо точки идут по разным путям (Рис. 1). Поэтому становиться актуальным введение новых правил для проведения расчетов электрических цепей.
При расчете электрических цепей в большинстве случаев нам встречаются цепи, образующие замкнутые контуры. В состав таких контуров, кроме сопротивлений, могут входить ЭДС (источники напряжений). На рисунке 4 представлен участок такой электрической цепи. Произвольно выбираем положительные направления токов. Обходим контур от точки А в произвольном направлении (выберем по часовой стрелке). Рассмотрим участок АБ: происходит падение потенциала (ток идет от точки с высшим потенциалом к точке с низшим потенциалом).
Первое правило Густава Кирхгофа сформулировано исходя из закона сохранения заряда. Физик понимал, что заряд не может задерживаться в узле, а распределяется по ветвям контура, образующим это соединение.
Кирхгоф предположил, а впоследствии обосновал на основании экспериментов, что количество зарядов зашедших в узел такое же, как и количество тока вытекающего из него.
На рисунке 1 изображена простая схема, состоящая из контуров. Точками A, B, C, D обозначены узлы контура в центре схемы.
Из третьего уравнения Максвелла вытекает правило Кирхгофа для напряжений. Его ещё называют вторым законом.
Это правило гласит, что в замкнутом контуре, на резистивных элементах, алгебраическая сумма напряжений (включая внутренние), равна сумме ЭДС, присутствующих в этом же замкнутом контуре.
При этом токи и ЭДС, векторы которых совпадают с направлением (выбирается произвольно) обхода контура, считаются положительными, а встречные к обходу токи – отрицательными.
Второй закон (правило) Кирхгофа, простыми словами
Второй закон Кирхгофа относят к замкнутым контурам, поэтому его называют правилом контуров. Согласно этому правилу суммы произведений алгебраических величин сил тока на внешние и внутренние сопротивления всех участков замкнутого контура равны алгебраической сумме величин сторонних ЭДС (), входящих в рассматриваемый контур. В виде формулы второй закон Кирхгофа запишем как:
где величину часто называют падением напряжения; N – число рассматриваемых участков избранного контура
При использовании второго правила Кирхгофа важно помнить о направлении обхода контура. Как это делается? Произвольно выберем направление обхода рассматриваемого в задаче контура (по часовой стрелке или против нее)
В случае совпадения направления обхода контура с направлением силы тока в рассматриваемом элементе, величина входит в (2) со знаком плюс. ЭДС войдет в сумму правой части выражения (2) со знаком плюс, если при движении вдоль контура, в соответствии с избранным направлением обхода первым мы встречаем отрицательный полюс источника ЭДС.
Используя второе правило Кирхгофа можно получить независимые уравнения для тех контуров цепи, которые не получены наложением уже описанных контуров. Количестов независимых контуров (n) равно:
где p – количество ветвей в цепи; k – число узлов.
Количество независимых уравнений, которые дадут оба правила Кирхгофа равно (s):
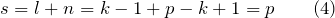
Делаем вывод о том, что число независимых уравнений будет равно числу разных токов в исследуемой цепи.
Второе правило Кирхгофа — следствие закона Ома. В принципе любую цепь можно рассчитать, применяя только закон Ома и закон сохранения заряда. Правила Кирхгофа являются всего лишь упрощающими приемами для решения задач, рассматривающих цепи постоянного тока.
Используя правила Кирхгофа для составления уравнений необходимо внимательно следить за расстановкой знаков токов и ЭДС.
Первое и второе правила Кирхгофа дают метод расчета цепи, то есть используя их можно найти все токи в цепи, если известны все ЭДС и сопротивления, в том числе и внутренние сопротивления источников.
Алгебраическая сумма разностей потенциалов
Закон напряжения по Густаву Кирхгофу — второй закон этого автора, используемый для анализа электрической схемы. Вторым законом Кирхгофа утверждается, что для последовательного замкнутого контура алгебраическая сумма всех напряжений по кругу любой замкнутой цепи равна нулю. Утверждение обусловлено тем, что контур цепи является замкнутым проводящим путём, где потери энергии исключаются. Другими словами, алгебраическая сумма разностей потенциалов замкнутого контура теоретически равняется нулю:
ΣV = 0
Следует обратить внимание: под термином «алгебраическая сумма» имеется в виду учёт полярностей и признаков источников ЭДС, а также падения напряжений по кругу контура. Эта концепция закона Кирхгофа, известная как «сохранение энергии», как движение по кругу замкнутого контура или схемы, утверждает логику возврата к началу цепи и к первоначальному потенциалу без потери напряжения по всему контуру
Отсюда следует вывод: применяя Второй закон Кирхгофа к определенному элементу электрической схемы, важно обращать особое внимание на алгебраические знаки падений напряжения на элементах (источниках ЭДС), иначе вычисления оборачиваются ошибкой
Одиночный контурный элемент — резистор
Простым примером с резистором предположим — ток протекает в том же направлении, что и поток положительного заряда. В этом случае поток тока через резистор протекает от точки A до точки B. Фактически — от положительной клеммы до отрицательной клеммы. Таким образом, поскольку движение положительного заряда отмечается в направлении аналогичном направлению течения тока, на резистивном элементе зафиксируется падение потенциала, которое приведет к падению минусового потенциала на резисторе (— I * R).
Если же поток тока от точки B до точки A протекает в противоположном направлении относительно потока положительного заряда, тогда через резистивный элемент отметится рост потенциала, поскольку имеет место переход от минусового потенциала к потенциалу плюсовому, что даёт падение напряжения (+ I * R). Таким образом, чтобы правильно применить закон Кирхгофа по напряжению к электрической цепи, необходимо точно определить направление полярности. Очевидно, знак падения напряжения на резисторе зависит от направления тока, протекающего через резистор.
Направление потока тока по замкнутому контуру допустимо определять либо по часовой стрелке, либо против часовой стрелки, и любой вариант допустим к выбору. Если выбранное направление отличается от фактического направления тока, соответствие закону Кирхгофа получится корректным и действительным, но приведет к результату, когда алгебраический расчёт будет иметь знак минус. Чтобы лучше понять эту концепцию, логично рассмотреть ещё один пример с одним контуром цепи на соответствие Второму Закону Кирхгофа.
Одиночный контур электрической цепи
Второй закон Кирхгофа утверждает — алгебраическая сумма разностей потенциалов любого замкнутого контура равна нулю. Демонстрационная схема действия Второго закона Кирхгофа для замкнутого контура с двумя резисторами и одним источником ЭДС. Если принять условие, что два резистора R1 и R2 соединены последовательно, оба элемента являются частью одного контура. Соответственно, одинаковый ток протекает через каждый из резисторов.
Таким образом, падение напряжения на резисторе R1 = I * R1 и падение напряжения на резисторе R2 = I * R2, дают напряжение по Второму закону Кирхгофа:
V = I * Rs
где: Rs = R1 + R2.
Очевидно: применение Второго закона Кирхгофа к одиночному замкнутому контуру даёт формулу эквивалентного или полного сопротивления для последовательной цепи. Допустимо расширить эту формулу, чтобы найти значения падений потенциалов по кругу контура:
I = V / Rs
Vr1 = V * (R1 / R1 + R2)
Vr2 = V * (R2 / R1 + R2)
Есть три резистора номинальным сопротивлением 10, 20, 30 Ом, соответственно. Все три резистивных элемента соединены последовательно к 12-вольтовому аккумулятору.
Требуется рассчитать:
- общее сопротивление,
- ток цепи,
- ток через каждый резистор,
- падение напряжения на каждом резисторе.
Рассчитаем общее сопротивление:
Ro = R1 + R2 + R3 = 10Ω + 20Ω + 30Ω = 60Ω
Ток цепи:
I = V / Ro = 12 / 60 = 0,2A (200 мА)
Ток через каждый резистор:
I * R1 = I * R2 = I * R3 = 0,2A (200 мА)
Падение потенциала на каждом из резисторов:
VR1 = I * R1 = 0.2 * 10 = 2В
VR2 = I * R2 = 0.2 * 20 = 4В
VR3 = I * R3 = 0.2 * 30 = 6В
Таким образом, Второй закон Кирхгофа справедлив, учитывая что индивидуальные падения напряжения, отмеченные по кругу замкнутого контура, в итоге составляют сумму напряжений.
Законы Кирхгофа для магнитной цепи
При расчетах разветвленных магнитных цепей пользуются двумя законами Кирхгофа, аналогичными законам Кирхгофа для электрической цепи.
Первый закон Кирхгофа непосредственно вытекает из непрерывности магнитных линий, т.е. и магнитного потока; алгебраическая сумма магнитных потоков в точке разветвления равна нулю:
Например, для узла а на рис. 6.11,б
— Ф1 — Ф2 + Ф3 = 0
Второй закон Кирхгофа для магнитной цепи основывается на законе полного тока: алгебраическая сумма магнитных напряжений на отдельных участках цепи равна алгебраической сумме МДС:
Например, для левого контура и а рис. 6.11, б Как следует из закона Ома, для получения наибольшего магнитного потока при наименьшей МДС у магнитной цепи должно быть возможно меньшее магнитное сопротивление. Большая магнитная проницаемость ферромагнитных материалов обеспечивает получение малых магнитных сопротивлений магнитопроводов из этих материалов. Поэтому магнитные цепи электрических машин выполняют преимущественно из ферромагнетиков, а участки цепей из неферромагнитных материалов, то есть неизбежные или необходимые воздушные зазоры, делают, как правило, возможно малыми.
Схема устройства магнитной цепи двухполюсной машины с явно выраженными полюсами показана на рис. 6.12.
Рис. 6.12 Магнитная цепь электрической машины с явно выраженными полюсами
Плоскость 00′, проведенная через середины полюсов N и S и ось машины, делит магнитную цепь на две симметричные части. В каждой из них магнитный поток Ф/2 замыкается через полюсы П, полюсные наконечники ПН, воздушные зазоры, якорь Я и станину машины С. Магнитодвижущая сила создается током в обмотке возбуждения ОВ, расположенной на полюсах N и S. Из северного полюса N магнитные линии выходят и в южный полюс S входят.
Рис, 6.13. Магнитная цепь электрической машины с неявно выраженными полюсами
Схема устройства магнитной цепи двухполюсной машины с неявно выраженными полюсами показана на рис. 6.13. Здесь обмотка возбуждения заложена в пазы ротора Р — вращающейся части машины, укрепленной на валу. Как и в предыдущем случае, плоскость 00′, проведенная через середины полюсов N и S, делит магнитную цепь машины на две симметричные части, в каждой из которых магнитный поток Ф/2. Магнитный поток замыкается через ротор машины, воздушные зазоры и станину машины С, представляющую собой неподвижный наружный стальной цилиндр — статор машины.
Магнитная цепь — последовательность магнетиков, по которым проходит магнитный поток. Различают замкнутые магнитные цепи, в которых магнитный поток почти полностью проходит в ферромагнитных телах, и с зазором (например, воздушным). Понятием магнитная цепь широко пользуются при электротехнических расчетах трансформаторов, электрических машин, реле и др. Простейшая магнитная цепь — сердечник кольцевой катушки.
Магнитодвижущая сила (МДС) — физическая величина, характеризующая способность электрических токов создавать магнитные потоки. Используется при расчетах магнитных цепей; аналог ЭДС в электрических цепях.
Величина измеряется в амперах (СИ) или же в гилбертах (СГС), причём 1А = = 1,257 Гб. На практике для обозначения единицы МДС часто используется термин «ампер-виток», численно равный единице в СИ.
Магнитодвижущая сила в индукторе или электромагните вычисляется по формуле:
где ω
— количество витков в обмотке,I — ток в проводнике.
Выражение для магнитного потока в магнитной цепи, также известное как закон Хопкинса, имеет следующий вид:
где — величина магнитного потока, — магнитное сопротивление проводника. Данная запись является аналогом закона Ома в магнитных цепях.
1 закон Кирхгофа
В цепях, состоящих из последовательно соединенных источника и приемника энергии, соотношения между током, сопротивлением и ЭДС всей цепи или на каком-либо участке цепи определяются законом Ома. Но на практике в цепях токи от какой-либо точки идут по разным путям (Рис. 1). Поэтому становиться актуальным введение новых правил для проведения расчетов электрических цепей.
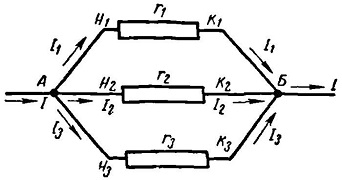
Рис. 1. Схема параллельного соединения проводников.
Так, при параллельном соединении проводников начала всех проводников соединены в одну точку, а концы проводников – в другую точку. Начало цепи присоединяется к одному полюсу источника напряжения, а конец цепи – к другому полюсу.
Из рисунка видно, что при параллельном соединении проводников для прохождения тока имеется несколько путей. Ток, протекая к точке разветвления А, растекается далее по трем сопротивлениям и равен сумме токов, выходящих из этой точки: I = I1 + I2 + I3.
Согласно первому правилу Кирхгофа алгебраическая сумма токов ветвей, сходящихся в каждом узле любой цепи равна нулю. При этом направленный к узлу ток принято считать положительным, а направленный от узла – отрицательным.
Запишем первый закон Кирхгофа в комплексной форме:
Первый закон Кирхгофа гласит, что алгебраическая сумма токов, направленных к узлу, равна сумме направленных от узла. То есть, сколько тока втекает в узел, столько же вытекает (как следствие закона сохранения электрического заряда). Алгебраическая сумма — это сумма, в которую входят слагаемые со знаком плюс и со знаком минус.
Рис. 2. i_1+i_4=i_2+i_3.
Рассмотрим применение 1 закона Кирхгофа на следующем примере:
- I1 – это полный ток, текущий к узлу А, а I2 и I3 — токи, вытекающие из узла А.
- Тогда мы можем записать: I1 = I2 + I3.
- Аналогично для узла B: I3 = I4 + I5.
- Пусть, что I4 = 5 А и I5 = 1 А, получим: I3 = 5 + 1 = 6 (А).
- Пусть I2 = 10 А, получим: I1 = I2 + I3 = 10 + 6 = 16 (А).
- Запишем подобное соотношение для узла C: I6 = I4 + I5 = 5 + 1 = 6 А.
- А для узла D: I1 = I2 + I6 = 10 + 6 = 16 А
- Таким образом мы наглядно видим справедливость первого закона Кирхгофа.