Законы Кирхгофа для расчёта электрических цепей
При расчёте электрических цепей, в том числе для целей моделирования, широко применяются законы Кирхгофа, позволяющие полностью определить режим её работы.
Воспользуйтесь программой онлайн-расчёта электрических цепей.
Прежде чем перейти к самим законам Кирхгофа, дадим определение ветвей и узлов электрической цепи.
Ветвью электрической цепи называется такой её участок, который состоит только из последовательно включённых источников ЭДС и сопротивлений, вдоль которого протекает один и тот же ток. Узлом электрической цепи называется место (точка) соединения трёх и более ветвей. При обходе по соединённым в узлах ветвям можно получить замкнутый контур электрической цепи. Каждый контур представляет собой замкнутый путь, проходящий по нескольким ветвям, при этом каждый узел в рассматриваемом контуре встречается не более одного раза .
Первый закон Кирхгофа
Первый закон Кирхгофа применяется к узлам и формулируется следующим образом: алгебраическая сумма токов в узле равна нулю:
∑i = 0,
или в комплексной форме
∑I = 0.
Второй закон Кирхгофа
Второй закон Кирхгофа применяется к контурам электрической цепи и формулируется следующим образом: в любом замкнутом контуре алгебраическая сумма напряжений на сопротивлениях, входящих в этот контур, равна алгебраической сумме ЭДС:
∑Z ∙ I = ∑E.
Количество уравнений, составляемых для электрической цепи по первому закону Кирхгофа, равно Nу – 1, где Nу – число узлов. Количество уравнений, составляемой для электрической цепи по второму закону Кирхгофа, равно Nв – Nу + 1, где Nв – число ветвей. Количество составляемых уравнений по второму закону Кирхгофа легко определить по виду схемы: для этого достаточно посчитать число «окошек» схемы, но с одним уточнением: следует помнить, что контур с источником тока не рассматривается.
Опишем методику составления уравнений по законам Кирхгофа. Рассмотрим её на примере электрической цепи, представленной на рис. 1.
Рис. 1. Рассматриваемая электрическая цепь
Для начала необходимо задать произвольно направления токов в ветвях и задать направления обхода контуров (рис. 2).
Рис. 2. Задание направления токов и направления обхода контуров для электрической цепи
Количество уравнений, составляемых по первому закону Кирхгофа, в данном случае равно 5 – 1 = 4. Количество уравнений, составляемых по второму закону Кирхгофа, равно 3, хотя «окошек» в данном случае 4. Но напомним, что «окошко», содержащее источник тока J1, не рассматривается.
Составим уравнения по первому закону Кирхгофа. Для этого «втекающие» в узел токи будем брать со знаком «+», а «вытекающие» — со знаком «-». Отсюда для узла «1 у.» уравнение по первому закону Кирхгофа будет выглядеть следующим образом:
I1 – I2 – I3 = 0;
для узла «2 у.» уравнение по первому закону Кирхгофа будет выглядеть следующим образом:
—I1 – I4 + I6 = 0;
для узла «3 у.»:
I2 + I4 + I5 – I7 = 0;
для узла «4 у.»:
I3 – I5 – J1 = 0
Уравнение для узла «5 у.» можно не составлять.
Составим уравнения по второму закону Кирхгофа. В этих уравнениях положительные значения для токов и ЭДС выбираются в том случае, если они совпадают с направлением обхода контура. Для контура «1 к.» уравнение по второму закону Кирхгофа будет выглядеть следующим образом:
ZC1 ∙ I1 + R2 ∙ I2 – ZL1 ∙ I4 = E1;
для контура «2 к.» уравнение по второму закону Кирхгофа будет выглядеть следующим образом:
-R2 ∙ I2 + R4 ∙ I3 + ZC2 ∙ I5 = E2;
для контура «3 к.»:
ZL1 ∙ I4 + (ZL2 + R1) ∙ I6 + R3 ∙ I7 = E3,
где ZC = — 1/(ωC), ZL = ωL.
Таким образом, для того, чтобы найти искомые токи, необходимо решить следующую систему уравнений:
В данном случае это система из 7 уравнений с 7 неизвестными. Для решения данной системы уравнений удобно пользоваться Matlab. Для этого представим эту систему уравнений в матричной форме:
Для решения данной системы уравнений воспользуемся следующим скриптом Matlab:
>> syms R1 R2 R3 R4 Zc1 Zc2 Zl1 Zl2 J1 E1 E2 E3; >> A = ; >> b = ; >> I = A\b
В результате получим вектор-столбец I токов из семи элементов, состоящий из искомых токов, записанный в общем виде. Видим, что программный комплекс Matlab позволяет существенно упростить решение сложных систем уравнений, составленных по законам Кирхгофа.
Список использованной литературы
- Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.
Рекомендуемые записи
- Метод контурных токов для расчёта электрических цепей При расчёте электрических цепей, помимо законов Кирхгофа, часто применяют метод контурных токов. Метод контурных токов…
- Метод фазных координат: пример расчёта матрицы передачи Расчёт матриц передачи многополюсников различной формы осуществляется достаточно просто. Матрицы передачи — это математическое описание рассматриваемой…
Составление уравнений
При расчете электрической цепи при помощи правил Кирхгофа составляются уравнения токов. Количество уравнений находится в прямой зависимости от числа узлов в цепи. Они используются для описания физических явлений и в промышленном секторе: при изготовлении жидкостных трубопроводов и электрических насосов.
При составлении уравнения нужно руководствоваться следующим алгоритмом:
- Выбрать направление потоков заряженных частиц на ветвях, обозначенных на электрической схеме.
- Отобрать напряжения с одинаковым направлением обхода закрытого контура.
- Выбрать контуры с разными ветвями и узлами для применения второго правила.
Многие физики сталкиваются с трудностями при составлении линейных уравнений для гальванической цепи, расположенной в сложных непланарных графах — математических объектах с минорами, полученными при помощи стягивания 1 ребра. В этом случае для расчета электрической цепи необходимо составить систему уравнений, где совмещены выражения как для первого, так и для второго законов Кирхгофа.
Для проверки правильности составления линейных используется потенциальная диаграмма, представляющая собой графическое изображение. Она строится для контура гальванической цепи. Если точки начала и конца диаграммы обладают идентичными потенциалами, независимыми от направления движения тока, то уравнение составлено верно.
Закон Кирхгофа для термодинамики
Кирхгоф показал, что соотношение излучательной и поглощательной способности твёрдого тела не зависит от вещества, но считается функцией частоты и температуры при термодинамическом равновесии. Особенно интересной абстракцией в этом плане стало абсолютно-чёрное тело. Это объект, поглощающий падающее на него излучение. Для него формула, представленная на рисунке упрощается. Излучающая способность абсолютно-чёрного тела описывает функцию формулы для прочих тел. Эта ипостась имеет максимум, определяемый законом смещения Вина и амплитуды, определяемую первым законом Вина (частным случаем считается формула Планка).
Отношение излучательной и поглощательной способности любого тела находится по формулам для любых температур и частот. При помощи спектрометра возможно оценить испускаемые волны. Это позволяют теоретически предсказать поглощательную способность любого предмета. На практике подобные исследования приводят к созданию объектов типа самолёт-невидимка, с трудом видимый локаторами.
Из закона сохранения энергии следует, что полное излучение равняется поглощению в термодинамическом равновесии. Значит, по всему спектру их соотношение равняется единице. До признания закона Кирхгофа уже установлено, что – чем лучше тело поглощает энергию, тем оно больше излучает
Обратите внимание, спектральные плотности поглощения и излучения имеют разную форму. В этом и заключается гениальное прозрение Кирхгофа
Взаимодействие определяется законом Вина и на графике выглядит подобно горе с вершиной, смещённой влево относительно центра фигуры.
Это позволяет понять, где находится максимум излучения (на макушке). Во всех участках графика, где линия находится ниже единицы, тело преимущественно поглощает энергию. Благодаря законам возможно предсказать температуру звёзд, к примеру, по цвету, а каждый кузнец знает, что деталь в горне дошла до кондиции лишь по характерному оттенку свечения. Это практические проявления законов Вина и Кирхгофа.
Вторым интересным наблюдением становится температура. Из графиков плотности излучения видно, чем показатель больше, тем активнее идёт излучение. В частности, звезды не поглощают энергию за малым исключением, но преимущественно излучают. У холодных планет преобладает противоположный процесс. Тело излучает, если его температура выше окружающей среды. В остальных ситуациях преобладает поглощение энергии.
Аналогия закона Кирхгофа
1.10. Правила Кирхгофа для разветвленных цепей
Для упрощения расчетов сложных электрических цепей, содержащих неоднородные участки, используются правила Кирхгофа, которые являются обобщением закона Ома на случай разветвленных цепей.
В разветвленных цепях можно выделить узловые точки (узлы), в которых сходятся не менее трех проводников (рис. 1.10.1). Токи, втекающие в узел, принято считать положительными; вытекающие из узла – отрицательными.
| Рисунок 1.10.1. Узел электрической цепи. I1, I2 > 0; I3, I4 <� 0 |
В узлах цепи постоянного тока не может происходить накопление зарядов. Отсюда следует первое правило Кирхгофа:
Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю:
| I1 + I2 + I3 + … + In = 0. |
Первое правило Кирхгофа является следствием закона сохранения электрического заряда.
В разветвленной цепи всегда можно выделить некоторое количество замкнутых путей, состоящих из однородных и неоднородных участков. Такие замкнутые пути называются контурами. На разных участках выделенного контура могут протекать различные токи. На рис. 1.10.2 представлен простой пример разветвленной цепи. Цепь содержит два узла a и d, в которых сходятся одинаковые токи; поэтому только один из узлов является независимым (a или d).
| Рисунок 1.10.2. Пример разветвленной электрической цепи. Цепь содержит один независимый узел (a или d) и два независимых контура (например, abcd и adef) |
В цепи можно выделить три контура abcd, adef и abcdef. Из них только два являются независимыми (например, abcd и adef), так как третий не содержит никаких новых участков.
Второе правило Кирхгофа является следствием обобщенного закона Ома.
Запишем обобщенный закон Ома для участков, составляющих один из контуров цепи, изображенной на рис. 1.10.2, например, abcd. Для этого на каждом участке нужно задать положительное направление тока и положительное направление обхода контура. При записи обобщенного закона Ома для каждого из участков необходимо соблюдать определенные «правила знаков», которые поясняются на рис. 1.10.3.
| Рисунок 1.10.3. «Правила знаков» |
Для участков контура abcd обобщенный закон Ома записывается в виде:
Для участка bc: I1R1 = Δφbc – 1.
Для участка da: I2R2 = Δφda – 2.
Складывая левые и правые части этих равенств и принимая во внимание, что Δφbc = – Δφda , получим:
| I1R1 + I2R2 = Δφbc + Δφda – 1 + 2 = –1 – 2. |
Аналогично, для контура adef можно записать:
| – I2R2 + I3R3 = 2 + 3. |
Второе правило Кирхгофа можно сформулировать так: алгебраическая сумма произведений сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока на этом участке равна алгебраической сумме ЭДС вдоль этого контура.
Первое и второе правила Кирхгофа, записанные для всех независимых узлов и контуров разветвленной цепи, дают в совокупности необходимое и достаточное число алгебраических уравнений для расчета значений напряжений и сил токов в электрической цепи. Для цепи, изображенной на рис. 1.10.2, система уравнений для определения трех неизвестных токов I1, I2 и I3 имеет вид:
| I1R1 + I2R2 = – 1 – 2, |
| – I2R2 + I3R3 = 2 + 3, |
| – I1 + I2 + I3 = 0. |
Таким образом, правила Кирхгофа сводят расчет разветвленной электрической цепи к решению системы линейных алгебраических уравнений. Это решение не вызывает принципиальных затруднений, однако, бывает весьма громоздким даже в случае достаточно простых цепей. Если в результате решения сила тока на каком-то участке оказывается отрицательной, то это означает, что ток на этом участке идет в направлении, противоположном выбранному положительному направлению.
| Модель. Цепи постоянного тока |
| Модель. Конденсаторы в цепях постоянного тока |
Законы Кирхгофа для расчёта электрических цепей
В цепях, состоящих из последовательно соединенных источника и приемника энергии, соотношения между током, сопротивлением и ЭДС всей цепи или на каком-либо участке цепи определяются законом Ома. Но на практике в цепях токи от какой-либо точки идут по разным путям (Рис. 1). Поэтому становиться актуальным введение новых правил для проведения расчетов электрических цепей.
При расчете электрических цепей в большинстве случаев нам встречаются цепи, образующие замкнутые контуры. В состав таких контуров, кроме сопротивлений, могут входить ЭДС (источники напряжений). На рисунке 4 представлен участок такой электрической цепи. Произвольно выбираем положительные направления токов. Обходим контур от точки А в произвольном направлении (выберем по часовой стрелке). Рассмотрим участок АБ: происходит падение потенциала (ток идет от точки с высшим потенциалом к точке с низшим потенциалом).
Первое правило Густава Кирхгофа сформулировано исходя из закона сохранения заряда. Физик понимал, что заряд не может задерживаться в узле, а распределяется по ветвям контура, образующим это соединение.
Кирхгоф предположил, а впоследствии обосновал на основании экспериментов, что количество зарядов зашедших в узел такое же, как и количество тока вытекающего из него.
На рисунке 1 изображена простая схема, состоящая из контуров. Точками A, B, C, D обозначены узлы контура в центре схемы.
Из третьего уравнения Максвелла вытекает правило Кирхгофа для напряжений. Его ещё называют вторым законом.
Это правило гласит, что в замкнутом контуре, на резистивных элементах, алгебраическая сумма напряжений (включая внутренние), равна сумме ЭДС, присутствующих в этом же замкнутом контуре.
При этом токи и ЭДС, векторы которых совпадают с направлением (выбирается произвольно) обхода контура, считаются положительными, а встречные к обходу токи – отрицательными.
№18 Законы Кирхгофа в цепях синусоидального тока. Методы расчета цепей синусоидального тока.
Для мгновенных значений ЭДС, токов и напряжений остаются справедливыми сформулированные ранее законы Кирхгофа.
Первый: в любой момент времени алгебраическая сумма токов в узле электрической цепи равна нулю:
где n — число ветвей, сходящихся в узле
Второй: в любой момент времени в замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме напряжений на всех остальных элементах контура:
где m — число ветвей, образующих контур
Токи, напряжения и ЭДС, входящие в уравнения (2.8) и (2.9), есть синусоидальные функции времени, которые мы рассматриваем как проекции некоторых векторов на оси координат. Так как сложению проекций соответствует сложение векторов и соответствующих им комплексных чисел, то справедливыми будут следующие уравнения, которые можно записывать как для действующих, так и для амплитудных значений.
Законы Киргофа в векторной форме
Законы Киргофа в символической форме
Из сказанного вытекают три возможных подхода к расчету цепей синусоидального тока: выполнение операций непосредственно над синусоидальными функциями времени по уравнениям выше; применение метода векторных диаграмм, использование в расчетах комплексных чисел и уравнений, являющихся основой символического метода.
Пример 2.4. В узле электрической цепи сходятся три ветви (рис. 18.1).
Токи первых двух ветвей известны:
Требуется записать выражение тока i3 и определить показания амперметров электромагнитной системы
Рис. 18.1 — Узел электрической цепи
Непосредственное сложение синусоид:
Сумма двух синусоид одинаковой чыстоты есть тоже синусоида той же частоты. Ее амплитуда и начальная фаза могут быть найдены по известным из математики формулам:
2. Применение метода векторных диаграмм.
В соответствии с первым законом Киргофа в векторной форме для цепи на рис. 18.1 имеем:
В прямоугольной системе координат строим векторы I1m и I2m и находим вектор I3m, равный их сумме (рис. 18.2)
Так как треугольник oab прямоугольный, а сторона ab равна длине вектора I2m, то:
Если треугольник получается не прямоугольным, то применяется теорема косинусов.
Начальная фаза третьего тока равна углу наклона: вектора I3m к горизонтальной оси:
Рис. 18.2 — Векторная диаграмма токов
3. Решение символическим методом
Записываем комплексные амплитуды первого и второго токов:
По первому закону Киргофа в символической форме
Модуль последнего комплексного числа равен амплитуде третьего тока, а агрумент — начальной фазе.
Определяем показания амперметров. Приборы электромагнитной системы показывают действующие значения токов и напряжений, потому:
Обращаем внимание на то, что I1+I2≠I3. Это не ошибка
В цепях синусоидального тока для показаний приборов законы Кирхгофа не справедливы. Можно складывать мгновенные значения токов (синусоидальные функции времени), векторы и комплексные числа, но не численные значения токов и напряжений, не показания приборов.
https://youtube.com/watch?v=6r4Y318cGhA
https://youtube.com/watch?v=f2rpF5ztAr0
§ 15. Второй закон Кирхгофа. Применение законов Кирхгофа для расчета электрических цепей
При расчете электрических цепей часто приходится встречаться с цепями, которые образуют замкнутые контуры. В состав таких контуров, помимо сопротивлений, могут входить еще электродвижущие силы.
На рис. 35 представлена часть сложной электрической цепи в виде замкнутого контура АБВГ. На схеме указаны полярность электродвижущих сил E1, E2, E3 и направления токов I1, I2, I3 и I4, протекающих на различных участках цепи.
Рис. 35. Участок сложной электрической цепи
Обходим контур от точки А в произвольном направлении, например по часовой стрелке. Рассмотрим каждый из участков рассматриваемого контура. На первом участке разность потенциалов между точками А и Б, или, что то же самое, напряжение UAБ, равна э.д.с. Е1 минус падение напряжения I1r1. Аналогично будет и на других участках цепи:
на участке АБ φА - φБ = Е1 - I1r1; на участке БВ φБ - φВ = -Е2 - I2r2; на участке ВГ φВ - φГ = E3 - I3r3; на участке ГА φГ - φА = I4r4.
Складывая левые и правые части уравнения, получим:
φA — φБ + φБ — φВ + φВ — φГ + φГ — φА = E1 — I1r1 — E2 — I2r2 + E3 I3r3 + I4r4;
0 = E1 — I1r1 — E2 — I2r2 + E3 — I3r3 + I4r4.
Перенося произведения (I⋅r) в одну часть, а электродвижущие силы (Е) в другую часть, получим
-E1 + E2 — E3 = — I1r1 — I2r2 — I3r3 + I4r4.
Или в общем виде
ΣE = ∑I ⋅ r.
Это выражение представляет собой второй закон Кирхгофа. Формула показывает, что во всяком замкнутом контуре алгебраическая сумма электродвижущих сил равна алгебраической сумме падений напряжений.
По второму закону Кирхгофа,
∑E = ∑Ir.
Для простейшей замкнутой цепи с одной э.д.с. Е (рис. 36)
E = Ir + Ir = I(r + r),
откуда
I = E/r+r.
Рис. 36. Простой замкнутый контур
Мы получили формулу закона Ома для замкнутой цепи.
Следовательно, закон Ома является частным случаем 2-го закона Кирхгофа.
При расчете электрических цепей применяют различные методы расчета. Выбор того или иного метода зависит от конфигурации цепи, числа э.д.с., заданных величин.
Как правило, расчет неразветвленных цепей с любым числом э.д.с., а также расчет сложных цепей с одной э.д.с. легче производить, применяя закон Ома.
Расчет сложных цепей с несколькими э.д.с. производят с помощью уравнений 1-го и 2-го законов Кирхгофа.
Расчет сложной цепи методом законов Кирхгофа производят в следующем порядке:
Условно задаются направлениями токов в различных участках цепи.
Определяют число уравнений, которое необходимо составить для решения задачи. Если известны все э.д.с. и сопротивления цепи, число уравнений должно быть равно числу неизвестных токов.
Для составления уравнений вначале используют уравнения 1-го закона Кирхгофа. Число уравнений 1-го закона Кирхгофа на единицу меньше числа узловых точек в схеме. Остальное число уравнений составляют по 2-му закону Кирхгофа.
Для этого намечают контуры, направление обхода этих контуров и приступают к составлению уравнений. Если направление обхода не совпадает с направлениями э.д.с. или с направлениями токов на отдельных участках контура, то величины э.д.с. и падения напряжения I⋅r входят в уравнения со знаком минус.
Решая систему уравнений, находят величину токов,
Если окажется, что в результате решения уравнений некоторые из токов получились отрицательными, то это значит, что направление этих токов было выбрано неправильно. Надо изменить направление токов на схеме.
Проверка правильности решения производится путем подстановки полученных значений токов в одно из составленных уравнений.
Решим несколько задач, используя закон Ома и оба закона Кирхгофа.
Пример 30. Найти токи в цепи, представленной на рис. 37. Выберем произвольно положительное направление тока. Обходя контур по часовой стрелке, пишем уравнение второго закона Кирхгофа:
-E1 + E2 = Ir1 + Ir2;
-1,9 + 1,3 = I(2 + 3);
-0,6 = 5I, I = -0,12 а.
Рис. 37. Электрическая цепь (к примеру 30)
Знак минус означает, что выбранное нами направление тока противоположно его действительному направлению.
Пример 31. Дана электрическая цепь (рис. 38). Определить токи на отдельных участках.
Рис. 38. Электрическая цепь (к примеру 31)
Произвольно выбираем положительные направления токов.
Для контура абде
6 = 2I1 + 5I3. (1)
Для контура авге
6 — 2 = 2I1 — 4I2. (2)
Для точки б, по первому закону Кирхгофа,
I3 = I1 + I2. (3)
Имеем три уравнения с тремя неизвестными. Решая их, находим величину и направление токов. Подставляя значение тока I3 из уравнения (3) в уравнение (1), получим
6 = 2I1 + 5I1 + 5I2; 6 = 7I1 + 5I2 + 2 = I1 - 2I2
или
12 = 14I1 + 10I2 + 10 = 5I1 + 10I2.
Складывая два последних уравнения, имеем:
22 = 19I1, откуда I1 = 1,156 а,
подставляем значение I1 в уравнение (1):
6 = 2 ⋅ 1,156 + 5I3,
| I3 = | 6 — 2 ⋅ 1,156 | = 0,74 а. |
| 5 |
Подставляем значение I1 в уравнение (2):
2 = 1,156 — 2I2,
откуда
| I2 = | — 2 + 1,156 | = — 0,422 a. |
| 2 |
Знак минус показывает, что действительное направление тока I2 обратно принятому нами направлению.
Ограничения
Законы Кирхгофа для схемы являются результатом модели с сосредоточенными элементами, и оба зависят от модели, применимой к рассматриваемой схеме. Когда модель неприменима, законы не применяются.
Текущий закон зависит от предположения, что чистый заряд в любом проводе, соединении или сосредоточенном компоненте постоянен. Когда электрическое поле между частями схемы не является незначительным, например, когда два провода имеют емкостную связь , это может быть не так. Это происходит в высокочастотных цепях переменного тока, где модель с сосредоточенными элементами больше не применима. Например, в линии передачи плотность заряда в проводнике будет постоянно колебаться.
В линии передачи чистый заряд в разных частях проводника изменяется со временем. В прямом физическом смысле это нарушает KCL.
С другой стороны, закон напряжения основан на том факте, что действие изменяющихся во времени магнитных полей ограничено отдельными компонентами, такими как индукторы. В действительности индуцированное электрическое поле, создаваемое индуктором, не ограничено, но поля утечки часто незначительны.
Моделирование реальных схем с сосредоточенными элементами
Приближение сосредоточенных элементов для схемы является точным на низких частотах. На более высоких частотах утечки потоков и различные плотности заряда в проводниках становятся значительными. В определенной степени такие схемы все еще можно моделировать с использованием паразитных компонентов . Если частоты слишком высоки, может быть более целесообразным моделировать поля напрямую, используя моделирование методом конечных элементов или другие методы .
Чтобы смоделировать схемы, чтобы можно было использовать оба закона, важно понимать разницу между физическими элементами схемы и идеальными элементами с сосредоточенными параметрами. Например, провод — не идеальный проводник
В отличие от идеального проводника, провода могут индуктивно и емкостно соединяться друг с другом (и с самими собой) и иметь конечную задержку распространения. Реальные проводники могут быть смоделированы в терминах сосредоточенных элементов с учетом паразитных емкостей, распределенных между проводниками, для моделирования емкостной связи или паразитных (взаимных) индуктивностей для моделирования индуктивной связи. Провода также имеют некоторую самоиндукцию, поэтому необходимы разделительные конденсаторы .
Демонстрация закона напряжений Кирхгофа в последовательной цепи
Давайте еще раз посмотрим на наш пример последовательной схемы, на этот раз нумеруя точки цепи для обозначения напряжений:
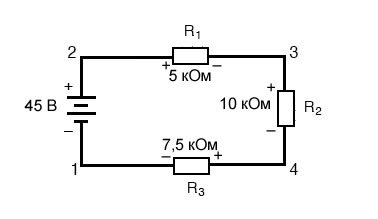
Если бы мы подключили вольтметр между точками 2 и 1, красный измерительный провод к точке 2 и черный измерительный провод к точке 1, вольтметр зарегистрировал бы значение +45 вольт. Для положительных показаний на дисплеях цифровых счетчиков знак «+» обычно не отображается, а скорее подразумевается. Однако для этого урока полярность показаний напряжений очень важна, поэтому я буду явно показывать положительные числа:
E2-1 = +45 В
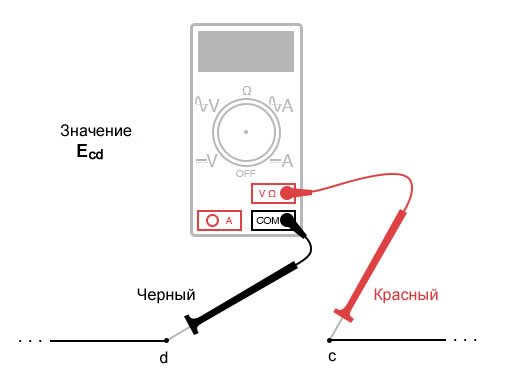
Когда напряжение указывается с двойным нижним индексом (символы «2-1» в обозначении «E2-1»), это означает напряжение в первой точке (2), измеренное по отношению ко второй точке (1). Напряжение, указанное как «Ecd», будет означать значение напряжения, показанное цифровым мультиметром с красным измерительным проводом в точке «c» и черным измерительным проводом в точке «d»: напряжение в точке «c» относительно точки «d».
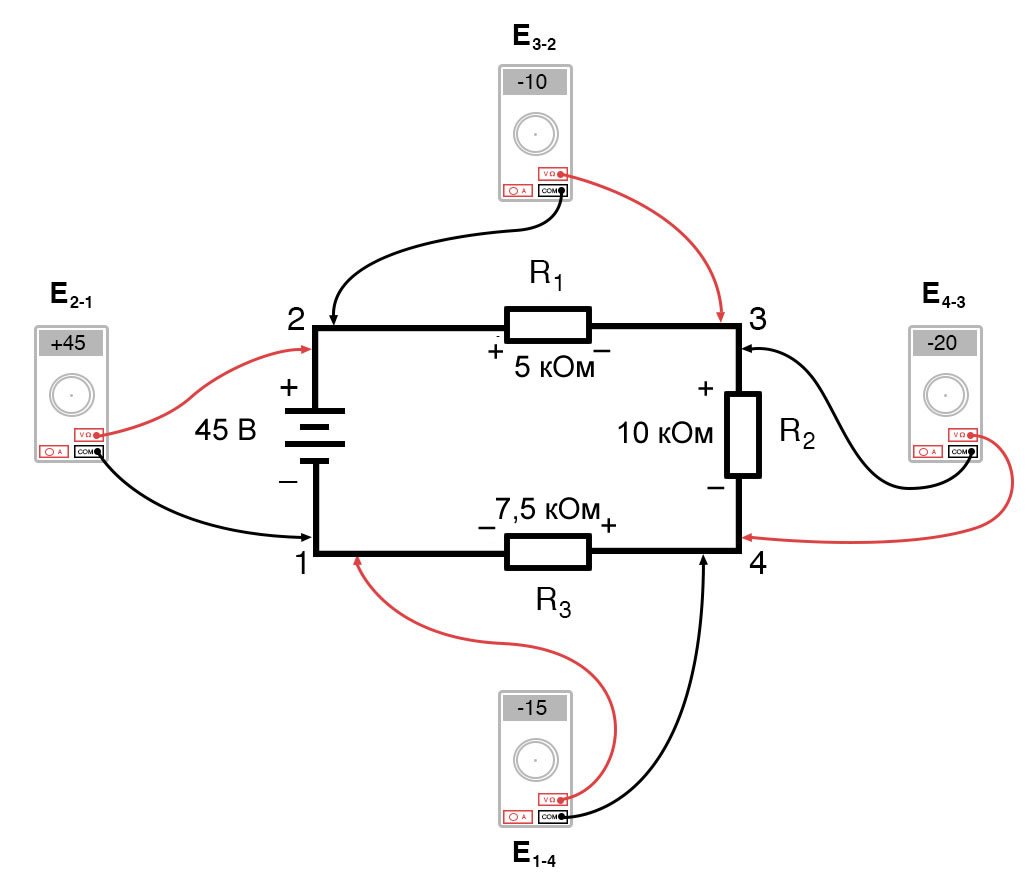
Если бы мы взяли тот же вольтметр и измерили падение напряжения на каждом резисторе, обходя цепь по часовой стрелке с красным измерительным проводом нашего мультиметра на точке впереди и черным измерительным проводом на точке позади, мы получили бы следующие показания:
E3-2 = -10 В
E4-3 = -20 В
E1-4 = -15 В
Нам уже должен быть знаком общий для последовательных цепей принцип, утверждающий, что отдельные падения напряжения в сумме составляют общее приложенное напряжение, но измерение падения напряжения таким образом и уделение внимания полярности (математическому знаку) показаний открывает еще один аспект этого принципа: все измеренные напряжения в сумме равны нулю:
В приведенном выше примере контур образован следующими точками в следующем порядке: 1-2-3-4-1. Не имеет значения, с какой точки мы начинаем или в каком направлении движемся при следовании по контуру; сумма напряжений по-прежнему будет равна нулю. Чтобы продемонстрировать это, мы можем той же цепи подсчитать напряжения в контуре 3-2-1-4-3:
Этот пример может быть более понятен, если мы перерисуем нашу последовательную схему так, чтобы все компоненты были представлены на одной прямой линии:
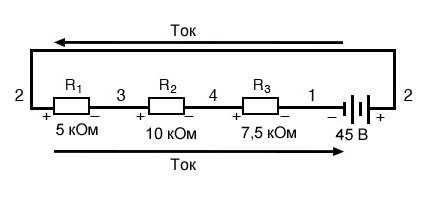
Это всё та же последовательная схема, только с немного перераспределенными компонентами
Обратите внимание на полярность падений напряжения на резисторах по отношению к напряжению батареи: напряжение батареи отрицательное слева и положительное справа, тогда как все падения напряжения на резисторах ориентированы в другую сторону (положительное слева и отрицательное справа). Это потому, что резисторы сопротивляются потоку электрического заряда, проталкиваемого батареей
Другими словами, «толкание», прилагаемое резисторами против потока электрического заряда, должно происходить в направлении, противоположном источнику электродвижущей силы.
Здесь мы видим, что цифровой вольтметр покажет на каждом компоненте в этой цепи, если черный провод будет слева, а красный провод – справа:
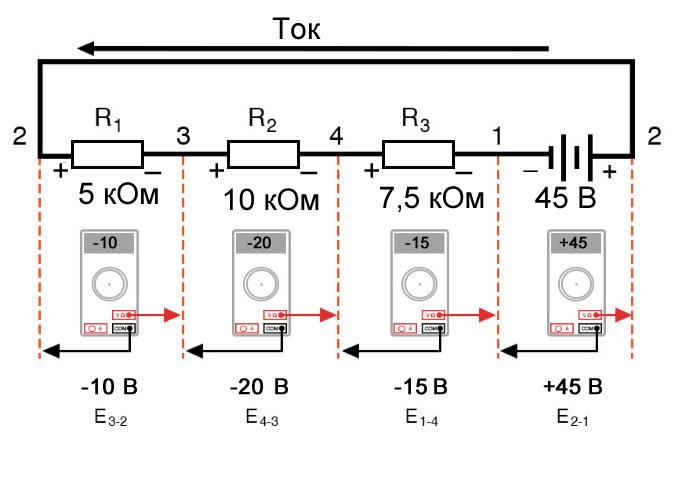
Если бы мы взяли тот же вольтметр и измерили напряжение между комбинациями компонентов, начиная с единственного R1 слева и продвигаясь по всей цепочке компонентов, мы увидели бы, как напряжения складываются алгебраически (до нуля):
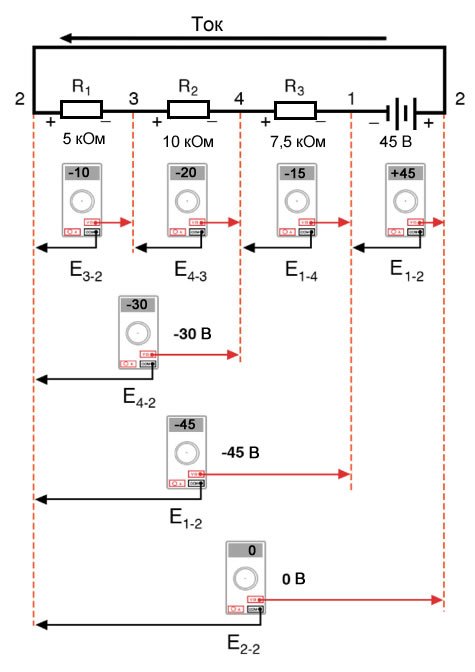
Тот факт, что последовательные напряжения складываются, не должен быть тайной, но мы заметили, что полярность этих напряжений имеет большое значение в том, как эти значения складываются. При измерении напряжения на R1 – R2 и R1 – R2 – R3 (я использую символ «двойное тире» «–» для обозначения последовательного соединения между резисторами R1, R2 и R3), мы видим, как измеряются бо́льшие значения напряжений (хотя и отрицательные), потому что полярности отдельных падений напряжения имеют одинаковую ориентацию (плюс слева, минус справа).
Сумма падений напряжения на R1, R2 и R3 равна 45 вольт, что соответствует выходному напряжению батареи, за исключением того, что полярность напряжения батареи (минус слева, плюс справа) противоположна падениям напряжения на резисторах, поэтому при измерении напряжения на всей цепочке компонентов мы получаем 0 вольт.
То, что мы должны получить ровно 0 вольт на всей линии, тоже не должно быть тайной. Глядя на схему, мы видим, что крайняя левая часть линии (левая сторона R1, точка номер 2) напрямую соединена с крайней правой частью линии (правая сторона батареи, точка номер 2), что необходимо для завершения схемы.
Поскольку эти две точки соединены напрямую, они являются электрически общими друг с другом. Таким образом, напряжение между этими двумя электрически общими точками должно быть равно нулю.
Второе правило Киргхофа
Из третьего уравнения Максвелла вытекает правило Кирхгофа для напряжений. Его ещё называют вторым законом.
При этом токи и ЭДС, векторы которых совпадают с направлением (выбирается произвольно) обхода контура, считаются положительными, а встречные к обходу токи – отрицательными.
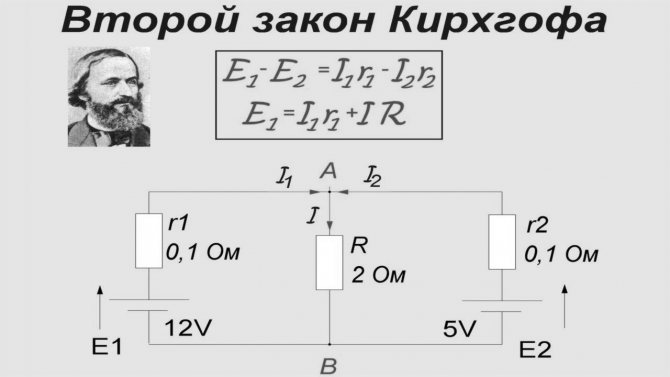
Рис. 4. Иллюстрация второго правила Кирхгофа
Формулы, которые изображены на рисунке применяются в частных случаях для вычисления параметров простых схем.
Формулировки уравнений общего характера:
, где где Lk и Ck – это индуктивности и ёмкости, соответственно.
Линейные уравнения справедливы как для линейных, так и для нелинейных линеаризованных цепей. Они применяются при любом характере временных изменений токов и напряжений, для разных источников ЭДС. При этом законы Кирхгофа справедливы и для магнитных цепей. Это позволяет выполнять вычисления для поиска соответствующие параметров.
Другие работы
Кирхгоф массу времени посвятил разным отраслям науки. К примеру, нашёл ошибку в постановке граничных условий для решения дифференциальных уравнений по колебаниям мембран, представленных на суд публики в 1811 году Софи Жермен. Не нужно думать, что словосочетание закон Кирхгофа узко ограничено двумя правилами, причём одно прямо приводит к сформулированному ранее закону Ома.
Учёный Г.Кирхгоф
Учёный представлен для получения звания члена-корреспондента Берлинской Академии наук в отделении математики, корреспондента Петербургской Академии наук. Если в первом случае заявители в основном указывали на дар в решении задач механики, наши соотечественники (Ленц и Якоби) немало отметили заслуги Кирхгофа в спектральном анализе.
Учёный преподавал, обладал феноменальной памятью, назубок читал длинные лекции без отступлений от формального текста. Чувство скрупулёзности помогало безукоризненно собирать материалы, и лишь недостаток технической оснастки помешал, вероятно, сделать новые открытия. К примеру, учёный отмечал, что одна из линий спектра кальция совпадает с железом, но не сумел достоверно сказать, кажущееся ли совпадение. Теперь известно, что длины волн отличаются на 5-6 ангстремов, но тогда на глаз сказать оказалось невозможно с полной уверенностью.
Закон кирхгофа расчет цепи
МЕТОД ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРА
Метод эквивалентного генератора рационально применять в том случае, когда требуется определить ток (или найти его аналитическое выражение) лишь в одной ветви цепи, без нахождения токов в остальных ветвях.
В основе метода лежит замена части цепи, подключенной к зажимам заданной ветви, эквивалентным источником и определение параметров этого источника. В зависимости от выбора вида эквивалентного источника различают метод эквивалентного генератора напряжения (источник ЭДС) или эквивалентного генератора тока (источник тока).
Расчёт методом эквивалентного генератора напряжения заключается в определении ЭДС и внутреннего сопротивления эквивалентного источника и состоит в следующем.
Закон Кирхгофа для теплового излучения
Данный закон имеет другое название «третий закон». Сперва для лучшего понимания введем понятие теплового излучения. Принято называть тепловым излучение электромагнитное излучение, возникающее благодаря чужеродной энергии вращательного и колебательного движения атомов, молекул. Данное явление можно обнаружить абсолютно у всех тел, имеющих температуру не равняющуюся нулю или меньше. Основной количественной характеристикой теплового излучения выступает энергетическая светимость. Она должна быть вычислена одной из первых или же указана в условиях. Рассчитать её самостоятельно весьма проблематично. Её значение не постоянное, оно может меняться в зависимости от определенных характеристик: оказывает влияние температура окружающей среды, а также уровень нагретости тела. Имеет значение и длина, чем длиннее — тем значение меньше.
Формула выглядит таким образом:
R = E/(S·t), [Дж/(м2с)] = [Вт/м2]
Ещё одной характеристикой остаётся спектральная плотность энергетической светимости.
Важно ввести ещё одно понятие: коэффициент поглощения – это отношение поглощенной телом энергии к падающей энергии. Только теперь перейдем непосредственно к выделенному закону. Первое, что нужно сказать, что тепловое излучение является равновесной величиной
Это указывает на то, что сколько энергии будет излучаться телом, столько и им же и поглотится. При расчётах данное заявление имеет существенное значение. Можно сразу приравнивать оба значение. Таким образом, для трёх тел, которые находятся в замкнутой полости, формула примет вид:
Первое, что нужно сказать, что тепловое излучение является равновесной величиной. Это указывает на то, что сколько энергии будет излучаться телом, столько и им же и поглотится. При расчётах данное заявление имеет существенное значение. Можно сразу приравнивать оба значение. Таким образом, для трёх тел, которые находятся в замкнутой полости, формула примет вид:
Закон для теплового излучения
Раннее указанная формула будет верной даже тогда, когда какое-либо тело из указанных будет АЧ:
Закон звучит данным образом: отношение спектральной плотности энергетической светимости тела к его монохроматическому коэффициенту поглощения (при определенной температуре и для определенной длины волны) не зависит от природы тела и равно для всех тел спектральной плотности энергетической светимости при тех же самых температуре и длине волны.