Суть метода контурных токов
Основные принципы данного метода основываются на том факте, что протекающие в ребрах цепи токи, не все считаются независимыми. Присутствующие в системе У-1 уравнения для узлов, четко показывают зависимость от них У-1 токов. При выделении в электрической цепи независимого тока Р-У+1, вся система может быть сокращена до уравнений Р-У+1. Таким образом, метод контурных токов представляет собой очень простое и удобное выделение в цепи независимых токов Р-У+1.
Использование данного способа расчетов допускает, что в каждом независимом контуре Р-У+1 осуществляется циркуляция определенного виртуального контурного тока. Если какое-либо ребро относится лишь к одному конкретному контуру, то значение протекающего в нем реального тока будет равно контурному. В том случае, когда ребро входит в состав сразу нескольких контуров, ток, протекающий в нем, будет представлять собой сумму, включающую в себя соответствующие контурные токи. В этом случае обязательно учитывается направление обхода контуров. Независимыми контурами перекрывается практически вся схема, поэтому ток, протекающий в каком угодно ребре может быть выражен путем контурных токов, составляющих полную систему всех токов.
Для того чтобы построить систему независимых контуров, используется простой и наглядный метод создания планарных графов. На данной схеме ветви и узлы цепи размещаются на плоскости таким образом, что взаимное пересечение ребер полностью исключается. С помощью этого метода плоскость разбивается на области, ограниченные замкнутыми цепочками ребер. Именно они и составляют систему независимых контуров. Данный метод более всего подходит для ручных расчетов схем. Однако его применение может стать затруднительным или вовсе невозможным, если рассматриваемая схема не укладывается в рамки планарного графа.
Другим способом расчетов служит метод выделения максимального дерева. Само дерево представлено в виде подмножества звеньев электрической цепи и является односвязным графом, в котором отсутствуют замкнутые контуры. Для того чтобы оно появилось, из цепи постепенно исключаются некоторые звенья. Дерево становится максимальным, когда к нему добавляется любое исключенное звено, в результате чего образуется контур.
Применение метода выделения максимального дерева представляет собой последовательное исключение из цепи заранее установленных звеньев в соответствии с определенными правилами. Каждый шаг в цепи предполагает произвольное исключение одного звена. Если такое исключение нарушает односвязность графа, разбивая его на две отдельные части, в этом случае звено может возвратиться обратно в цепь. Если граф остается односвязным, то и звено остается исключенным. В конечном итоге, количество звеньев, исключенных из цепи, оказывается равным количеству независимых контуров, расположенных в схеме. Получение каждого нового независимого контура связано с присоединением к электрической цепи конкретного исключенного звена.
Переменный ток.
В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками.
Последним этапом находим действительные токи, для этого нужно записать для них выражения. Работа активного двухполюсника под нагрузкой в номинальном режиме определяется уравнением 1.
Определим параметры электрической цепи рис. Неуправляемые нелинейные элементы имеют одну вольт-амперную характеристику; управляемые — семейство характеристик.
Определить ток I1 в заданной по условию схеме с источником тока, используя метод эквивалентного генератора. Чтобы решить такую систему можно воспользоваться программой MathCad. В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений.
Читайте дополнительно: Нормы прокладки кабеля под землей
АГЗ МЧС РГР №1 Расчёт линейных цепей постоянного тока
Уравнения по второму закону составляют для независимых контуров. Определим параметры электрической цепи рис. Контурный ток равен действительному току, который принадлежит только этому контуру. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений.
Направление обхода контура совпадает с направлением контурных токов. Режим работы электрической цепи рис. Переменный синусоидальный ток или напряжение задается уравнением: Здесь Im — амплитуда тока. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем. Метод контурных токов заключается в том, что вместо токов в ветвях определяются, на основании второго закона Кирхгофа, так называемые контурные токи, замыкающиеся в контурах.
Определить токи во всех ветвях схемы на основании метода наложения.
Эта вольт-амперная характеристика строится по двум точкам 1 и 2 рис. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Следовательно, схема источника тока рис. Вычислим коэффициент подобия.
Составить баланс мощностей в исходной схеме схеме с источником тока , вычислив суммарную мощность источников и суммарную мощность нагрузок сопротивлений. Рекомендуется узлы схемы a, b, c, d заменить на 1, 2, 3, 4 соответственно. Исключением служат цепи, содержащие более сложные соединения звездой и треугольником. В нашем случае эти токи направлены по часовой стрелке. Законы Кирхгофа — Теория и задача
Сборник задач по электротехнике с решениями. Учебное пособие
В первое время после включения показаний амперметра в цепи обмотки I1 = 1,2 А, а после нагрева обмотки до установившейся температуры I2 = 1 А. Учитывая, что температура воздуха в помещении 20 °С
| и | температурный | коэффициент | сопротивления | меди | |||||
| 4 10–3 K–1, найти температуру обмотки. | |||||||||
| 1.1.15) Определить сопротивление проводов воздушной линии при температурах +40 и –40 °С. Дли- | |||||||||
| на линии l = 28,5 км, диаметр медных проводов d = 5 мм. | |||||||||
| 1.1.16) Приемник | за | пять | суток | непрерывной | работы | израсходовал | |||
| 24 кВт ч электроэнергии при напряжении 220 В. Определить ток и сопротивление приемника. | |||||||||
| 1.1.17) Определить плотность тока в проводах диаметром 4 мм, соединяющих приемник с генерато- | |||||||||
| ром. Суточная выработка энергии генератора, составляет 48 кВт ч при напряжении U = 220 В. | |||||||||
| U | 1.1.18) Электрическая | цепь | мощностью | P | = | 5 | кВт | при | напряжении |
| = | 220 | В | подключена | к | генератору | с | внутренним | сопротивлением |
Rвт = 0,22 Ом. Определить эдс и кпд генератора.
1.1.19) Механическая мощность электродвигателя постоянного тока 8,5 кВт при напряжении U = 220 В, кпд 85 %. Определить электрическую мощность и ток двигателя.
1.1.20) На изготовление катушки израсходовано 200 м медного провода диаметром 0,5 мм. На какое постоянное напряжение можно включать эту катушку, если допустимая плотность тока j = 2 А/мм2?
1.1.21) Составить схему электрической цепи, в которой к аккумуляторной батарее присоединены три резистора. Один – регулируемый, включен последовательно с группой из двух нерегулируемых, соединенных между собой параллельно. В схеме предусмотреть управление с помощью двухполюсного выключателя, защиту плавкими предохранителями, измерение общего тока в цепи и напряжения на зажимах батареи.
1.1.22) Составить схему электрической цепи, в которой четыре резистора (один из них регулируемый) образуют замкнутый контур в виде четырехугольника. В одной диагонали четырехугольника – гальванический элемент, присоединенный к цепи через однополюсный выключатель, в другой находится гальванометр, который можно включить и выключить кнопочным выключателем.
1.1.23) Составить схему электрической цепи, в которой последовательно включены два нерегулируемых резистора, аккумуляторная батарея и генератор, которые можно включить согласно или встречно. В схеме предусмотреть защиту цепи плавкими предохранителями, измерение тока, измерение напряжения на зажимах батареи и генератора одним вольтметром с помощью переключателя.
1.1.24) Составить схему электрической цепи, в которой генератор постоянного тока и аккумуляторная батарея, включенные параллельно, снабжают энергией внешнюю часть цепи, состоящей из трех нерегулируемых резисторов, включенных также параллельно. Каждый элемент цепи присоединяется к ней однополюсным выключателем. В схеме предусмотреть измерение общего напряжения, тока в каждом источнике и общего тока приемников энергии.
1.1.25) Два генератора постоянного тока, работая круглосуточно на общий приемник, выработали вместе за месяц 96 000 кВт ч энергии. В течение 10 суток этого месяца первый генератор находился в ремонте. За это время счетчик электрической энергии, установленный на линии к приемнику, показал 2 400 кВт ч. Определить мощность и эдс каждого генератора, если амперметр в цепи первого генератора во время работы показывал 500 А, а в цепи второго – 100 А.
1.1.26) Источник электрической энергии имеет в качестве нагрузки реостат с переменным сопротивлением R, эдс источника Е = 24 В, а его внутреннее сопротивление R = 1 Ом. Построить графики зависимости напряжения U на зажимах источника, мощности источника Pи, мощности приемника Pп, кпд источника, мощности потерь внутри источника Pвт от тока в цепи при изменении сопротивления нагрузки от R = ∞ (холостой ход) до R = 0 (короткое замыкание), считая эдс источника постоянной.
1.2ЗАКОН ОМА
1В электрической цепи за положительное направление эдс Е принимается направление, совпадающее с силой, действующей на положительный заряд, т.е. от «–» источника к «+» источника питания.
За положительное направление напряжения U принято направление, совпадающее с направлением действия электрического поля, т.е. от «+» к «–» источника.
Порядок расчёта:
1. Произвольно задаёмся направлением токов в ветвях.
Важно! При выборе направления токов в ветвях, необходимо выполнения двух условий:1. Ток должен вытекать из узла через одну или несколько других ветвей;2
Хотя бы один ток должен входить в узел.
Красным выделены изменения после первого действия
Синим выделены изменения после третьего пункта
2. Используя первый закон Кирхгофа составим уравнения для (n-1) узлов схемы. Где n – число узлов. То есть для схемы с четырьмя узлами, составляем три уравнения. Для этого:
- Обозначаем узлы буквами.
- Берём один конкретный узел (Например узел А) и смотрим как направлены токи в ветвях образующих узел. Если ток направлен в узел, то записываем его со знаком плюс, если из него то со знаком минус.
0=I1-I4-I6 (Полученное уравнение) -
Повторяем пункт B ещё для двух узлов.0=-I3+I4+I5(Узел В)
0=I3-I1-I2(Узел D)
3. Используя второй закон Кирхгофа составим уравнения для каждого контура схемы. Для этого произвольно зададимся направлением обхода контура (по часовой или против часовой). Для контура ABDA направление обхода контура выберем по часовой стрелке.
3.1 Смотрим, как направлена ЭДС относительно обхода контура. Если направление обхода контура совпадает, то значение ЭДС записываем со знаком плюс (в левой части уравнения), если не совпадает, то со знаком минус (записываем также в левой части уравнения)
3.2 Смотрим, как направлено падение напряжения на сопротивлении контура.(То есть смотрим как направлены токи, только записываем в уравнение произведение тока на сопротивление через которое ток протекает в данном контуре). Если направление обхода контура совпадает, то падение напряжения записываем со знаком плюс (в правой части уравнения), если не совпадает, то со знаком минус (записываем также в правой части уравнения)
3.3 Произвести действия 3.1 и 3.2 для остальных контуров. У вас должна получится система из n уравнений, где n — количество контуров в цепи.
Контур ABDA E1=I1*(R1+R01)+I4*R4+I3*R3
Контур BCDB E2=I2*(R2+R02)+I3*R3+I5*R5
Контур ABCA 0=I6*R6-I4*R4+I5*R5
4. Решаем полученную систему уравнений и находим величины токов во всех ветвях.
Уберём лишние токи из системы используя уравнения полученные во втором пункте поскольку у нас три уравнения поэтому мы оставляем только три любых тока. Для данного примера я рекомендую оставить токи I1 I2 I4.
0=I1-I4-I6 (Узел А)
0=-I3+I4+I5(Узел В)
0=I3-I1-I2(Узел D)
Выражаем из трёх уравнений токи I3 I5 I6 через токи I1 I2 I4.
I6=I1-I4(Узел А)
I3=I1+I2(Узел D)
I5=I3-I4(Узел В)
I5=I3-I4(Узел В) В этом уравнении сразу не получилось выразить I5 через токи I1 I2 I4, поэтому вместо тока I3 подставим уравнение для узла D и получим:
I5=I1+I2-I4
Заменим токи I3 I5 I6 и получим уравнения с тремя токами :
E1=I1*(R1+R01)+I4*R4+(I1+I2)*R3
E2=I2*(R2+R02)+(I1+I2)*R3+(I1+I2-I4)*R5
0=(I1-I4)*R6-I4*R4+(I1+I2-I4)*R5
Раскрываем скобки подставляем значения сопротивлений из условия и получаем например вот такие три уравнения:
40 = 71*I1 + 24*I2 + 14*I4
20 = 55*I1 + 93*I2 — 61*I4
0 = 60*I1 + 16*I2 — 81*I4
Дальше для решения системы можно воспользоваться .
Если при решении системы ток получается отрицательным (со знаком —), значит его действительное направление противоположно тому направлению которое мы задали в первом действии.
Правильность решения можно проверить с помощью баланса мощностей.
Законы Кирхгофа. Расчет цепей постоянного тока
В электротехнике существует два основных закона, на основании которых, теоретически можно решить все цепи.
Первый закон Кирхгофа выглядит следующим образом. Сумма токов, входящих в узел, равна сумме токов, отходящих от узла.
Для данного рисунка имеем: I1 + I2 + I4 = I3 + I5.
Второй закон Кирхгофа. Сумма напряжений вдоль замкнутого контура равна сумме ЭДС вдоль этого же контура. Для схемы на рисунке (стрелкой обозначим направление вдоль контура, которое будем считать условно положительным).
Начиная с узла, где сходятся токи I1, I3, I4 запишем все напряжения (по закону Ома): -I1⋅R1 — I1⋅R2 – в первой ветви (знак минус означает, что ток имеет направление противоположное выбранному направлению контура). I3⋅R3 – во второй ветви (знак «плюс», направление совпадает).
Теперь запишем ЭДС: E2 — E3 (знак «минус» у E3, потому что направление ЭДС противоположно направлению контура).
В соответствии с законом Кирхгофа напряжения равны ЭДС: -I1⋅R1 — I1⋅R2 + I3⋅R3 = E2 — E3.
Как видите, все довольно просто.
В большинстве случаев перед студентами стоит задача рассчитать величины токов во всех ветвях, зная величины ЭДС и резисторов. Для расчета сложной, разветвленной цепи постоянного тока, например этой, найденной на просторах интернета, воспользуемся следующими действиями.
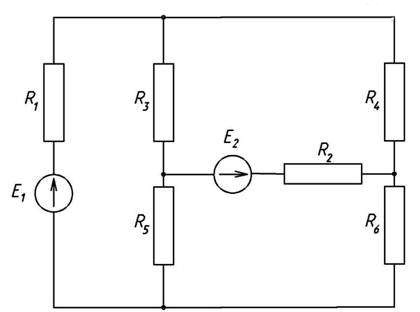
Для начала задаемся условно положительными направлениями токов в ветвях (это значит, что ток может течь и в противоположном направлении, тогда он будет иметь отрицательное значение).
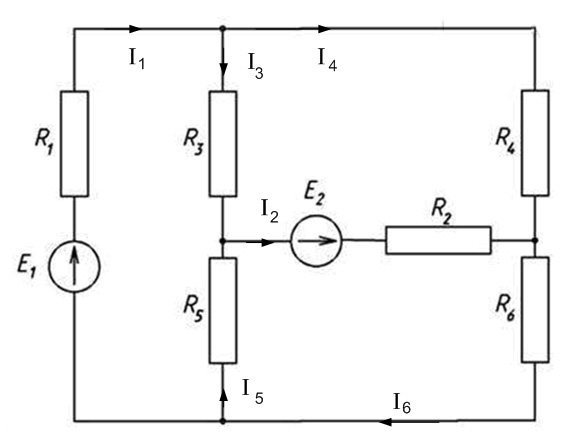
Составляем систему уравнений по второму закону Кирхгофа для каждого замкнутого контура так, чтобы охватить каждый неизвестный ток (в данной схеме имеем 3 таких контура). Направления контуров выбираем для удобства по часовой стрелке (хоть это и необязательно):
По первому закону Кирхгофа составляем столько уравнений, чтоб охватить все неизвестные токи (в данной схеме для любых трех узлов):
Итого, имеем систему из 6 уравнений. Чтобы решить такую систему можно воспользоваться программой MathCad. Решается она следующим образом:

Это скриншот программы. Знак «равно» в уравнения должен быть жирным (вкладка «булевы», CTRL + “=/+”). MathCad может решать системы любого порядка (например, схема имеет 10 независимых контуров). Но, во-первых, функция “Given” не работает с комплексными числами (об этом позже), во-вторых, не всегда есть под рукой компьютер или условие задачи поставлено так, что требуется решить схему другим методом.
Данный метод решения задач называется методом непосредственного применения законов Кирхгофа. Большинство студентов старших курсов (уже прослушавших курс ТОЭ), инженеров-электриков, даже преподавателей и докторов наук могут решать схемы только этим методом, т.к. другие методы применяются крайне редко.
Метод узловых (потенциалов) напряжений
ТОЭ › Методы расчета цепей постоянного тока
При изучении основ электротехники приходится сталкиваться с необходимостью расчета тех или иных параметров различных схем. И самое простое, что приходится делать – это расчет токов ветвей в цепях постоянного тока.
Существует несколько наиболее применяемых методов расчетов для таких цепей: с помощью законов Кирхгофа, методом контурных токов, узловых потенциалов, методом эквивалентного генератора, эквивалентного источника тока, методом наложения. Для расчета более сложных цепей, например, в нелинейных схемах, могут применяться метод аппроксимации, графические методы и другие. В данном разделе рассмотрим один из методов определения токов в цепи постоянного тока – метод узловых потенциалов.
Важно отличать метод узловых напряжений (потенциалов) от метода узлового напряжения (метод двух узлов)
Метод узловых потенциалов примеры решения задач
Для того, чтобы лучше разобраться в этом вопросе, рассмотрим конкретный пример схемы, показанной на рис.1.
Рис.1. Схема постоянного тока
Для начала обозначают направления токов в ветвях. Направление можно выбирать любым. Если в результате вычислений какой-то из токов получится с отрицательным значением, значит, его направление в действительности будет направлено в противоположную сторону относительно ранее обозначенного. Если в ветви имеется источник, то для удобства лучше обозначить направление тока в этой ветви совпадающим с направлением источника в этой ветви, хотя и не обязательно. Далее один из узлов схемы заземляем. Заземленный узел будет называться опорным, или базисным. Такой метод заземления на общее токораспределение в схеме влияния не оказывает.
Какой именно узел заземлять, значения не имеет. Заземлим, например, узел 4 φ4 = 0.
Каждый из этих узлов будет обладать своим значением потенциала относительно узла 4. Именно значения этих потенциалов для дальнейшего определения токов и находят. Соответственно, для удобства этим потенциалам присваивают номера в соответствии с номером узла, т.е. φ1, φ2, φ3. Далее составляется система уравнений для оставшихся узлов 1, 2, 3.
В общем виде система имеет вид:
Использованные в этой системе уравнений буквенно-цифровые обозначения
имеют следующий смысл:
– сумма проводимостей ветвей, сходящихся в узле 1. В данном случае
– сумма проводимостей ветвей, сходящихся в узле 2. В данном случае
– сумма проводимостей ветвей, сходящихся в узле 3. В данном случае
– сумма проводимостей ветвей, соединяющих узлы 1 и 2, взятая со знаком «минус». Для этого единица и взята с отрицательным знаком:
– сумма проводимостей ветвей, соединяющих узлы 1 и 3, взятая со знаком «минус». Для этого единица и в этом случае взята с отрицательным знаком:
Аналогично находятся и остальные проводимости:
J11 – узловой ток узла 1, в котором участвуют ветви, подходящие именно к этому узлу, и содержащие в своем составе ЭДС. При этом, если ЭДС ветви, входящий в узел, направлена к рассматриваемому узлу (в данном случае к узлу 1), то такой узловой ток записывается с плюсом, если от узла, то с минусом. В данном случае
Аналогично
В результате всех ранее приведенных вычисленных значений исходная система уравнений примет вид:
Решать данную систему можно всеми доступными методами, мы же для упрощения решим ее в пакете Mathcad:
В результате получены следующие значения потенциалов в узлах цепи:
Токи в ветвях находятся в соответствии с законом Ома. Поясним это простыми словами.
В ветви с сопротивлением и источником, учитывая ранее обозначенное направление тока в рассматриваемой ветви, необходимо из потенциала узла, находящегося у начала стрелки направления тока, вычесть потенциал узла, находящегося у конца стрелки направления тока, а затем прибавить значение ЭДС в этой ветви. Далее все это разделить на сопротивление, имеющееся в ветви. Если бы ток и ЭДС в рассматриваемой ветви не совпадали по направлению, тогда значение ЭДС вычиталось. В ветви без ЭДС действует то же самое правило, только ЭДС в числителе, разумеется, отсутствует. В нашем примере получим, что
Значение тока первой ветви, как видно из расчета, получилось отрицательным. Значит, в действительности, этот ток направлен в противоположную сторону относительно его обозначенного направления на рис.1.
Правильность расчетов можно проверить, например, составлением баланса мощностей либо, к примеру, моделированием, схемы. Выполним моделирование в программе Multisim.
Рис.2. Моделирование в Multisim
Как видим, результаты моделирования совпадают с расчетными значениями. Незначительная разница в тысячных долях из-за округлений промежуточных вычислений.
Расчет цепи методом контурных токов.
Метод контурных токов.
Метод контурных токов дает возможность упростить расчет электрических цепей по сравнению с методом расчета по законам Кирхгофа за счет уменьшения числа уравнений, которые приходится решать совместно. Этот метод заключается в том, что вместо токов в ветвях определяются на основании второго закона Кирхгофа так называемые контурные токи, замыкающиеся в контурах. На рис. 1.22. в виде примера показана двухконтурная цепь, в которой I11 и I22 — контурные токи. Токи в сопротивлениях r1 и r2 равны соответствующим контурным токам; ток в сопротивлении r3 являющемся общим для обоих контуров, равен разности контурных токов I11 и I22, так как эти токи направлены в ветви r3 встречно.
Число уравнений , записываемых для контурных токов по второму закону Кирхгофа, равно числу независимых контуров, то есть для электрической схемы с числом узлов q и числом ветвей p задача нахождения контурных токов сведется к решению системы p-q +1 уравнений. Так, в схеме рис. 1.22 q = 2 p = 3; следовательно, число уравнений равно 3-2+1=2 (число уравнений независимых контуров).
Положительные направления контурных токов задаются произвольно. Направление обхода каждого контура принимается обычно совпадающим с выбранным положительным направлением контурного тока; поэтому при составлении уравнения по второму закону Кирхгофа падение напряжения от заданного контурного тока в сопротивлениях, входящих в контур, берется со знаком плюс. Падение напряжения от тока смежного контура в общем сопротивлении берется со знаком минус, если контурные токи в этом сопротивлении направлены встречно, как это, например, имеет место в схеме рис. 1.22, где направление обоих контурных токов выбрано по ходу часовой стрелки.
Для заданной электрической схемы с двумя независимыми контурами (рис.1.22) могут быть записаны два уравнения по второму закону Кирхгофа, а именно:
, ,
здесь (r1 + r3) и (r2 + r3) — собственные сопротивления контуров 1 и 2, r3 —
общее сопротивление контуров 1 и 2. После определения контурных токов, легко найти и токи всех ветвей.
I1 = I11; I2 = I22 ; I3 = I11 — I22 .
Баланс мощностей.
Все расчеты в электрических цепях проверяют балансом мощностей
Баланс основан на законе сохранения и превращения энергии: сколько энергии выработали источники, столько же ее нагрузки должны потребить. Вместо энергии в балансе можно использовать мощность. Выработанная мощность всеми источниками должна быть равна суммарной мощности, расходуемой в нагрузках.
Баланс мощностей можно сформулировать так: алгебраическая сумма мощностей источников, должна быть равна арифметической сумме мощностей нагрузок. Если направление ЭДС и направление тока ветви не совпадают, то составляющая мощности этого источника в балансе мощностей берется со знаком «минус».
Мощность, отдаваемая источниками ЭДС, равна.
| PИ = E I |
Если в резисторе не происходит химических реакций, то мощность выделяется в форме тепла, согласно известному закону Джоуля.
| PП = R I2 |
где: I — постоянный ток (А), протекающий через резистор; PП — мощность потерь, измеряемая в ваттах (Вт); R — сопротивление резистора (Ом).
Равенство выражений мощностей источников и мощностей приемников называется уравнением баланса мощностей.
План составления баланса мощностей
1. Если в цепи есть источники тока, то следует любым методом найти напряжения на зажимах источников тока Uk.
| Цепи с источником тока |
2. вычислить мощность источников.
| PИ = | n | m | |
| k = 1 | Uk * Jk + | k = 1 | Ek * Ik |
3. где: N — количество источников тока в цепи; M — количество источников ЭДС в цепи; Uk — напряжение на источниках тока Jk;
| m | |
| k = 1 | Ek * Ik |
—
алгебраическая сумма, здесь положительны те из слагаемых, для которых направления ЭДС Еk и соответствующего тока Ik совпадают, в противном случаи слагаемое отрицательно;
n
| k = 1 | Uk * Jk |
—
алгебраическая сумма, здесь положительны те из слагаемых, для которых направление напряжения на зажимах источника тока Uk и направление его тока Jk во внешней цепи совпадают, в противном случаи слагаемое отрицательно.
PП =
L
k = 1
I2k * Rk
5. где:
| L | — | количество приемников в цепи; |
| L | ||
| k = 1 | I2k * Rk |
—
арифметическая сумма, здесь должны быть учтены как внешние резисторы, так и внутренние сопротивления самих источников.
6. Получаем равенство.
| РИ = РП |
Метод контурных токов | Онлайн журнал электрика
Методика расчета цепи способом контурных токов
В способе контурных токов за неведомые величины принимаются расчетные (контурные) токи, которые типо протекают в каждом из независящих контуров. Таким макаром, количество неведомых токов и уравнений в системе равно числу независящих контуров цепи.
Расчет токов веток по способу контурных токов делают в последующем порядке:
1 Вычерчиваем принципную схему цепи и обозначаем все элементы.
2 Определяем все независящие контуры.
3 Произвольно задаемся направлением протекания контурных токов в каждом из независящих контуров (по часовой стрелке либо против). Обозначаем эти токи. Для нумерации контурных токов можно использовать арабские сдвоенные числа (I11, I22, I33 и т. д.) либо римские числа.
4 По второму закону Кирхгофа, относительно контурных токов, составляем уравнения для всех независящих контуров. При записи равенства считать, что направление обхода контура, для которого составляется уравнение, совпадает с направлением контурного тока данного контура. Следует учесть и тот факт, что в смежных ветвях, принадлежащих двум контурам, протекают два контурных тока. Падение напряжения на потребителях в таких ветвях нужно брать от каждого тока в отдельности.
5 Решаем хоть каким способом полученную систему относительно контурных токов и определяем их.
6 Произвольно задаемся направлением реальных токов всех веток и обозначаем их. Маркировать реальные токи нужно таким макаром, чтоб не путать с контурными. Для нумерации реальных токов можно использовать одиночные арабские числа (I1, I2, I3 и т. д.).
7 Перебегаем от контурных токов к реальным, считая, что реальный ток ветки равен алгебраической сумме контурных токов, протекающих по данной ветки.
При алгебраическом суммировании без конфигурации знака берется контурный ток, направление которого совпадает с принятым направлением реального тока ветки. В неприятном случае контурный ток множится на минус единицу.
Пример расчёта сложной цепи способом контурных токов
В цепи, изображённой на рисунке 1, высчитать все токи способом контурных токов. Характеристики цепи: Е1 = 24 В, Е2 = 12 В, r1 = r2 = 4 Ом, r3 = 1 Ом, r4 = 3 Ом.
Рис. 1. Схема электронной цепи для примера расчета по способу контурных токов
Решение. Для расчета сложной цепи этим способом довольно составить два уравнения, по числу независящих контуров. Контурные токи направляем по часовой стрелке и обозначаем I11 и I22 (см. набросок 1).
По второму закону Кирхгофа относительно контурных токов составляем уравнения:
Решаем систему и получаем контурные токи I11 = I22 = 3 А.
Произвольно задаемся направлением реальных токов всех веток и обозначаем их. На рисунке 1 такими токами являются I1, I2, I3. Направление у этих токов однообразное – вертикально ввысь.
Перебегаем от контурных токов к реальным. В первой ветки протекает только один контурный ток I11. Направление его совпадает с направлением реального тока ветки. В таком случае реальный ток I1 + I11 = 3 А.
Реальный ток 2-ой ветки формируется 2-мя контурными I11 и I22. Ток I22 совпадает по направлению с реальным, а I11 ориентирован навстречу реальному. В итоге I2 = I22 — I11 = 3 — 3 = 0А.
В третьей ветки протекает только контурный ток I22. Направление этого тока обратно направлению реального, потому для I3 можно записать I3 = -I22 = -3А.
Необходимо подчеркнуть, как положительный факт, что в способе контурных токов по сопоставлению с решением по законам Кихгофа приходится решать систему уравнений наименьшего порядка. Но этот способ не позволяет сходу определять реальные токи веток.
Пацкевич В. А.
Школа для электрика