§ 35. направление тока и направление линий его магнитного поля

Каково определение, магнитное поле..??

Роджер

В современной физике «Магнитное поле» рассматривается как одно из силовых полей, приводящее к действию магнитной силы на движущиеся электрические заряды. Магнитное поле создается движущимися электрическими зарядами, как правило, электрическими токами, а также переменным электрическим полем. Существует гипотеза о возможности существования магнитных зарядов, что в принципе не запрещается электродинамикой, однако пока такие заряды (магнитные монополи) не обнаружены. В рамках электродинамики Максвелла магнитное поле оказалось тесно связанным с электрическим полем, что привело к возникновению единого понятия электромагнитное поле.
Полевая физика несколько меняет отношение к магнитному полю. Во-первых, она доказывает, что магнитных зарядов в принципе не может существовать. Во-вторых, магнитное поле оказывается не самостоятельным полем, равноправным электрическому, а одной из трех динамических поправок, возникающих при движении электрических зарядов. Поэтому полевая физика рассматривает в качестве фундаментального только электрическое поле, а магнитная сила становится одной из производных электрического взаимодействия.
P.S. профессор, конечно, лопух, но аппаратура при нем….

Мари

Магни́тное по́ле — составляющая электромагнитного поля, появляющаяся при наличии изменяющегося во времени электрического поля. Кроме того магнитное поле может создаваться током заряженных частиц, либо магнитными моментами электронов в атомах (постоянные магниты) . Основной характеристикой магнитного поля является его сила, определяемая вектором магнитной индукции \vec{\mathbf{B}}. В СИ магнитная индукция измеряется в Тесла (Тл) .
Физические свойства
Магнитное поле формируется изменяющимся во времени электрическим полем либо собственными магнитными моментами частиц. Кроме того магнитное поле может создаваться током заряженных частиц. В простых случаях оно может быть найдено из закона Био — Савара — Лапласа или теоремы о циркуляции (она же — закон Ампера) . В более сложных ситуациях ищется как решение уравнений Максвелла
Магнитное поле проявляется в воздействии на магнитные моменты частиц и тел, на движущиеся заряженные частицы (или проводники с током) . Сила, действующая на движущуюся в магнитном поле заряженную частицу называется силой Лоренца. Она пропорциональна заряду частицы и векторному произведению поля и скорости движения частицы.
Математическое представление
Векторная величина, образующая в пространстве поле с нулевой дивергенцией.

3.21. Движение зарядов в магнитном поле

1) Вектор скорости перпендикулярен силовым линиям.

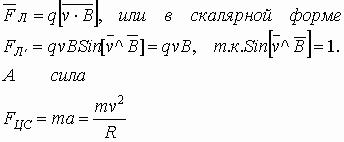направленная перпендикулярно скорости – центростремительная.

Скорость изменяется только по направлению, но не по величине. Сила Лоренца, действующая на движущуюся частицу в магнитном поле, закручивает траекторию движения в окружность, то есть появляется центростремительное ускорение: значит v изменяется только по направлению, но не по величине. Тогда приравняем

,

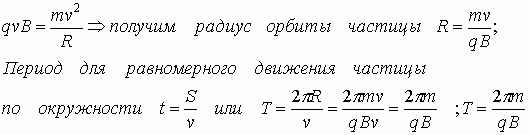где Т – период обращения заряда по орбите

2) угол между направлением скорости и силовыми линиями не равен 90 градусам.

, 0<α<90

Дальнейший анализ траектории движения частицы относительно вектора скорости аналогичен пункту 1).

Здесь сила Лоренца

. Новой характеристикой здесь является l — шаг спирали.

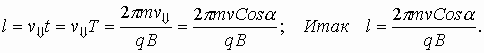
Приложение:

1. если частица движется вдоль силовых линий магнитного поля, то сила Лоренца равна нулю.
2. Если частица неподвижна в магнитном поле, то сила Лоренца также равна нулю.

ФИЗИКА

§ 38. Магнитный поток

На рисунке 116, а изображён проволочный контур, помещённый в однородное магнитное поле. Принято говорить, что контур в магнитном поле пронизывается определённым магнитным потоком Ф, или потоком вектора магнитной индукции.

Рис. 116. Зависимость магнитного потока, пронизывающего площадь контура, от модуля вектора магнитной индукции, площади контура и от ориентации плоскости контура по отношению к линиям магнитной индукции

Опыты показывают, что магнитный поток сквозь контур пропорционален модулю вектора индукции однородного магнитного поля и площади, ограниченной этим контуром. Кроме того, магнитный поток зависит от того, как расположена плоскость контура по отношению к линиям магнитной индукции.

Допустим, что индукция магнитного поля, пронизывающего ограниченную контуром площадь, стала больше. Это могло произойти, например, в результате увеличения силы тока, создающего это магнитное поле, или при перемещении контура в другое, более сильное поле.

Поскольку магнитный поток пропорционален индукции магнитного поля, то при её увеличении в n раз (от значения В₁ до значения В₂ = nВ₁, как показано на рис. 116, а, б) во столько же раз возрастёт и поток Ф, пронизывающий площадь S данного контура.

При том же самом магнитном поле с индукцией В₁ магнитный поток, пронизывающий большую площадь S’ (рис. 116, в), будет во столько же раз больше потока через площадь S (см. рис. 116, а), во сколько раз S’ больше, чем S.

Если плоскость контура перпендикулярна линиям магнитной индукции (см. рис. 116, а), то при данной индукции В₁ поток Ф, пронизывающий ограниченную этим контуром площадь S, максимален.

При вращении контура вокруг оси ОО’ проходящий сквозь него магнитный поток уменьшается (по закону косинуса) и становится равным нулю, когда плоскость контура располагается параллельно линиям магнитной индукции (рис. 116, г). В этом случае линии магнитной индукции как бы скользят по плоскости рамки, не пронизывая её.

Таким образом, магнитный поток, пронизывающий площадь контура, меняется при изменении модуля вектора магнитной индукции й, площади контура S и при вращении контура, т. е. при изменении его ориентации по отношению к линиям индукции магнитного поля.

Если же контур вращается так, что при любом его положении линии магнитной индукции лежат в плоскости контура, не пересекая ограниченную им площадь (рис. 117), то поток не меняется: в любой момент времени он равен нулю.

Рис. 117. Магнитный поток равен нулю, если линии магнитнойиндукции лежат в плоскости контура

Вопросы

1. От чего зависит магнитный поток, пронизывающий площадь плоского контура, помещённого в однородное магнитное поле?
2. Как меняется магнитный поток при увеличении в п раз магнитной индукции, если ни площадь, ни ориентация контура не меняются?
3. При какой ориентации контура по отношению к линиям магнитной индукции магнитный поток, пронизывающий площадь этого контура, максимален; равен нулю?
4. Меняется ли магнитный поток при таком вращении контура, когда линии магнитной индукции то пронизывают его, то скользят по его плоскости?

Упражнение 35

Проволочная катушка К₁ со стальным сердечником включена в цепь источника постоянного тока последовательно с реостатом R и ключом К (рис. 118). Электрический ток, протекающий по виткам катушки K₁ создаёт в пространстве вокруг неё магнитное поле. В поле катушки K₁ находится такая же катушка К₂.

Рис. 118

Каким образом можно менять магнитный поток, пронизывающий катушку К₂? Рассмотрите все возможные варианты.

Магнитное поле

Магнитное поле — одна из форм электромагнитного поля.

Магнитное поле создается движущимися электрическими зарядами и спиновыми магнитными моментами атомных носителей магнетизма (электронов, протонов и др.). Полное описание электрических и магнитных полей и их взаимосвязь дают Максвелла уравнения.

Магнитное поле, силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения. Магнитное поле характеризуется вектором магнитной индукции В, который определяет: силу, действующую в данной точке поля на движущийся электрический заряд (Лоренца сила); действие магнитного поля на тела, имеющие магнитный момент, а также другие свойства магнитного поля.

Впервые термин «Магнитное поле» ввёл в 1845 году английский физик, основоположник учения об электромагнитном поле Майкл Фарадей, считавший, что как электрические так и магнитные взаимодействия осуществляются посредством единого материального поля. Классическая теория электромагнитного поля была создана Джеймсом Клерком Максвеллом (1873 год), квантовая теория — в 20-х годах 20 века (Квантовая теория поля).

Источниками макроскопического магнитного поля являются намагниченные тела, проводники с током и движущиеся электрически заряженные тела. Природа этих источников едина: магнитное поле возникает в результате движения заряженных микрочастиц (электронов, протонов, ионов), а также благодаря наличию у микрочастиц собственного (спинового) магнитного момента.

Магнитные поля в природе

Магнитные поля в природе чрезвычайно разнообразны как по своим масштабам, так и по вызываемым ими эффектам.

Магнитное поле Земли, образующее земную магнитосферу, простирается до расстояния в 70-80 тысяч км в направлении на Солнце и на многие миллионы км в противоположном направлении. У поверхности Земли поле равно в среднем 0,5 гс, на границе магнитосферы ~ 10-3 гс. Геомагнитное поле экранирует поверхность Земли и биосферу от потока заряженных частиц солнечного ветра и частично космических лучей.

Влияние самого геомагнитного поля на жизнедеятельность организмов изучает магнитобиология. В околоземном пространстве магнитное поле образует магнитную ловушку для заряженных частиц высоких энергий — радиационный пояс Земли. Содержащиеся в радиационном поясе частицы представляют значительную опасность при полётах в космос. Происхождение магнитного поля Земли связывают с конвективными движениями проводящего жидкого вещества в земном ядре (Земной магнетизм).

Непосредственные измерения при помощи космических аппаратов показали, что ближайшие к Земле космические тела — Луна, планеты Венера и Марс не имеют собственного магнитного поля, подобного земному. Из других планет Солнечной системы лишь Юпитер и, по-видимому, Сатурн обладают собственными магнитными полями, достаточными для создания планетарных магнитных ловушек.

На Юпитере обнаружены магнитные поля до 10 гс и ряд характерных явлений (магнитные бури, синхротронное радиоизлучение и другие), указывающих на значительную роль магнитных полей в планетарных процессах.

3.4. Закон Био-Савара–Лапласа

3.4.1. Магнитное поле проводника с током

В общем случае для определения магнитного поля от произвольного проводника с произвольным знаком протекания тока проводим дифференцирование. Определяем полную индукцию, как сумму элементарных индукций от элементов тока dl, содержащих dq движущегося заряда.

Согласно последнему утверждению, совпадает с перпендикуляром к плоскости, образованной векторами cкорости и радиус- вектора

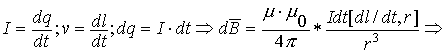Пользуясь известными формулами, получим:

Последняя формула и есть закон Био-Савара-Лапласа для определения магнитной индукции для проводника с током.

Примем условиями: . Тогда Переведем в скалярную форму и выразим геометрические величины через один параметр, параметр a: 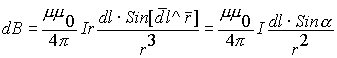; Используем условия геометрии: 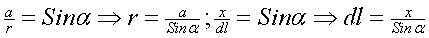при условии, что: 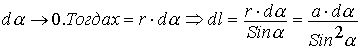Подставляя полученное в формулу для dB, получаем: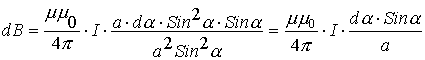

Это выражение для составляющей магнитного поля в точке p элемента проводника с током dl. Тогда полное магнитное поле проводника с током в искомой точке принимает вид:

Назовем предельные углы α₁ и α₂ как углы, под которыми из искомой точки видны концы проводника, создающего магнитное поле. Тогда для конечного проводника с током это будет выглядеть так:

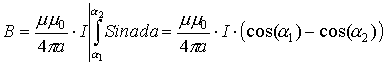. Если проводник бесконечен, т.е. , то: ; . Тогда .

3.4.3. Магнитное поле кругового проводника с током

Направление магнитного поля (B) внутри кругового проводника с током также подчиняется правилу буравчика (шляпка как ток, буравчик как индукция). Магнитное поле элемента dl кругового проводника с током:

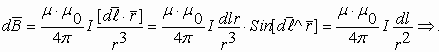Тогда для замкнутого проводника с током в центре витка магнитное поле определится как: 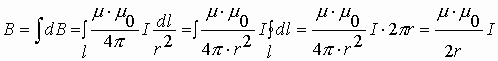— Магнитная индукция кругового проводника (контура) с током в центре контура.

3.4.4. Магнитное поле вдали от центра контура с током

Элементы контура с током dl создают в точке А элементарные индукции dB, являющиеся трехмерным образованием в виде конуса, который дает результирующую B, равную:

Это магнитное поле на оси контура с током. При : (смотри формулу для центра контура)

3.4.5. Магнитное поле соленоида

Если контура с током последовательно соединить в одном месте пространства, то такое образование называется соленоидом.

В таком соленоиде магнитные потоки от последовательно соединенных контуров суммируются. Так как магнитные силовые линии замкнутые, то внутри соленоида число силовых линий равно числу силовых линий всего соленоида.

А раз объем внутри соленоида ограничен, то можно сказать, что магнитное поле сконцентрировано внутри соленоида, снаружи рассеяно, и магнитные силовые линии внутри соленоида параллельны между собой и поле внутри соленоида считается однородным, вне соленоида — неоднородным. Величина магнитной индукции внутри соленоида записывается так:

, где μ — среда внутри соленоида, N — число витков соленоида, l — длина соленоида. Если обозначить — удельное число витков

3.24. Приложение к теореме Остроградского-Гаусса

Для любого вектора a можно записать его поток:

Так как интегрирование и дифференцирование по сути своей противоположные операции, то можно записать, например:

Интегрирование и дифференцирование по одному и тому же параметру по сути взаимно компенсирующие операции. Тогда можно записать для вектора а:

Где dV=dx*dy*dz.

А так же:

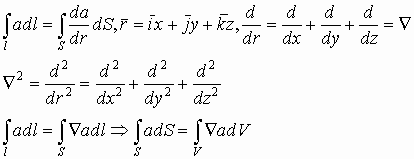
Таким образом, можно связать линейный, поверхностный и объемный интегралы, т.е. можно переходить от линейного к поверхностному, и от поверхностного к объёмному интегралу.

Приложение к теореме Остроградского-Гаусса мы используем при рассмотрении уравнений Максвелла.

Магнитное поле Земли

Наша планета на протяжении нескольких миллиардов лет является огромным магнитом. Индукция магнитного поля Земли изменяется в зависимости от координат. На экваторе она равна примерно 3,1 на 10 в минус пятой степени Тесла. К тому же существуют магнитные аномалии, где значение и направление поля существенно отличаются от соседних областей. Одни из самых крупных магнитных аномалий на планете — Курская и Бразильская магнитные аномалии.

Происхождение магнитного поля Земли до сих пор остается загадкой для ученых. Предполагается, что источником поля является жидкое металлическое ядро Земли.  Ядро движется, значит, движется расплавленный железо-никелевый сплав, а движение заряженных частиц – это и есть электрический ток, порождающий магнитное поле. Проблема в том, что эта теория (геодинамо) не объясняет того, как поле сохраняется устойчивым.

Магнитное поле земли

Земля – огромный магнитный диполь. Магнитные полюса не совпадают с географическими, хотя и находятся в непосредственной близости. Более того, магнитные полюса Земли движутся. Их смещение регистрируется с 1885 года. Например, за последние сто лет магнитный полюс в Южном полушарии сместился почти на 900 километров и сейчас находится в Южном океане. Полюс арктического полушария движется через Северный Ледовитый океан к Восточно-Сибирской магнитной аномалии, скорость его передвижения (по данным 2004 года) составила около 60 километров в год. Сейчас наблюдается ускорение движения полюсов — в среднем скорость растет на 3 километра в год.

Каково значение магнитного поля Земли для нас? В первую очередь магнитное поле Земли защищает планету от космических лучей и солнечного ветра. Заряженные частицы из далекого космоса не падают прямо на землю, а отклоняются гигантским магнитом и движутся вдоль его силовых линий. Таким образом, все живое оказывается защищенным от пагубной радиации.

Магнитное поле Земли

За историю Земли происходило несколько инверсий (смен) магнитных полюсов. Инверсия полюсов – это когда они меняются местами. Последний раз это явление произошло около 800 тысяч лет назад, а всего геомагнитных инверсий в истории Земли было более 400. Некоторые ученые полагают, что с учетом наблюдающегося ускорения движения магнитных полюсов следующей инверсии полюсов следует ожидать в ближайшие пару тысяч лет.

К счастью, в нашем веке смены полюсов пока не ожидается. А значит, можно думать о приятном и наслаждаться жизнью в старом добром постоянном поле Земли, рассмотрев основные свойства и характеристики магнитного поля.

Основные уравнения

Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в огромное множество уравнений, иногда непосредственно, иногда через связанную с ним напряжённость магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, это пожалуй разве только чистая электростатика.

(Здесь формулы приведем в СИ, в виде для вакуума, где есть варианты для вакуума — для среды; запись в другом виде и подробности — см. по ссылкам).

В магнитостатике

В магнитостатическом пределе наиболее важными являются:

• Закон Био — Савара — Лапласа: играет в магнитостатике ту же роль, что закон Кулона в электростатике:

  B→(r→)=μ4π∫L1I(r→1)dL1→×(r→−r→1)|r→−r→1|3,{\displaystyle {\vec {B}}\left({\vec {r}}\right)={\mu _{0} \over 4\pi }\int \limits _{L_{1}}{\frac {I\left({\vec {r}}_{1}\right){\vec {dL_{1}}}\times \left({\vec {r}}-{\vec {r}}_{1}\right)}{\left|{\vec {r}}-{\vec {r}}_{1}\right|^{3}}},}

  B→(r→)=μ4π∫j→(r→1)dV1×(r→−r→1)|r→−r→1|3,{\displaystyle {\vec {B}}\left({\vec {r}}\right)={\mu _{0} \over 4\pi }\int {\frac {{\vec {j}}\left({\vec {r}}_{1}\right)dV_{1}\times \left({\vec {r}}-{\vec {r}}_{1}\right)}{\left|{\vec {r}}-{\vec {r}}_{1}\right|^{3}}},}

• Теорема Ампера о циркуляции магнитного поля:

  ∮∂S⁡B→⋅dl→=μIS≡μ∫Sj→⋅dS→,{\displaystyle \oint \limits _{\partial S}{\vec {B}}\cdot {\vec {dl}}=\mu _{0}I_{S}\equiv \mu _{0}\int \limits _{S}{\vec {j}}\cdot {\vec {dS}},}

  rotB→≡∇→×B→=μj→.{\displaystyle \mathrm {rot} \,{\vec {B}}\equiv {\vec {\nabla }}\times {\vec {B}}=\mu _{0}{\vec {j}}.}

В общем случае

Основные уравнения (классической) электродинамики общего случая (то есть независимо от ограничений магнитостатики), в которых участвует вектор магнитной индукции B→{\displaystyle {\vec {B}}}:

Три из четырех уравнений Максвелла (основных уравнений электродинамики)

divE→=ρε,   rotE→=−∂B→∂t{\displaystyle \mathrm {div} \,{\vec {E}}={\frac {\rho }{\varepsilon _{0}}},\ \ \ \mathrm {rot} \,{\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}}}

divB→=,    rotB→=μj→+1c2∂E→∂t{\displaystyle \mathrm {div} \,{\vec {B}}=0,\ \ \ \ \,\mathrm {rot} \,{\vec {B}}=\mu _{0}{\vec {j}}+{\frac {1}{c^{2}}}{\frac {\partial {\vec {E}}}{\partial t}}}

а именно:

Закон отсутствия монополя:

divB→=,{\displaystyle \mathrm {div} \,{\vec {B}}=0,}

Закон электромагнитной индукции Фарадея:

rotE→=−∂B→∂t,{\displaystyle \mathrm {rot} \,{\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}},}

Закон Ампера — Максвелла:

rotB→=μj→+1c2∂E→∂t.{\displaystyle \mathrm {rot} \,{\vec {B}}=\mu _{0}{\vec {j}}+{\frac {1}{c^{2}}}{\frac {\partial {\vec {E}}}{\partial t}}.}

Формула силы Лоренца:

F→=qE→+qv→×B→,{\displaystyle {\vec {F}}=q{\vec {E}}+q\left,}

Следствия из неё, такие как

Выражение для силы Ампера, действующей со стороны магнитного поля на ток (участок провода с током)

dF→=Idl→×B→,{\displaystyle d{\vec {F}}=\left,}

dF→=j→dV×B→,{\displaystyle d{\vec {F}}=\left,}

выражение для момента силы, действующего со стороны магнитного поля на магнитный диполь (виток с током, катушку или постоянный магнит):

M→=m→×B→,{\displaystyle {\vec {M}}={\vec {m}}\times {\vec {B}},}

выражение для потенциальной энергии магнитного диполя в магнитном поле:

U=−m→⋅B→,{\displaystyle U=-{\vec {m}}\cdot {\vec {B}},}

• а также следующих из них выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле и т. д..
• Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:

F→=Kqmr→r3.{\displaystyle {\vec {F}}=K{\frac {q_{m}{\vec {r}}}{r^{3}}}.}

(это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).

Выражение для плотности энергии магнитного поля

w=B22μ{\displaystyle w={\frac {B^{2}}{2\mu _{0}}}}

Оно в свою очередь входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля и в лагранжиан электромагнитного поля и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).

3.20. Магнетики. Вещества в магнитном поле

Вещества, способные намагничиваться и влиять на направление вектора магнитной индукции внешнего поля B, называются магнетиками.

Способность намагничиваться — создание собственного магнитного поля в веществе, которое или усиливает, или уменьшает внешнее магнитное поле.

Собственные магнитные свойства вещества определяются электронами, связанными с атомами. Строение атома подразумевает наличие электрона e, вращающегося вокруг ядра. Магнитный момент электрона , то есть каждая орбита электрона в атоме обладает собственным магнитным моментом и создает собственное магнитное поле. В целом в веществе суммарные магнитные моменты электронов в атоме расположены хаотично и их сумма зачастую равна нулю.

Под действием внешнего магнитного поля собственные магнитные поля, созданные электронами, упорядочиваются. Это и есть явление намагниченности. Оно может сохраняться после снятия магнитного поля, а может и исчезать. У ферромагнетиков оно сохраняется, а у диа и парамагнетиков исчезает.

В результате поле равно: , где каппа — магнитная восприимчивость, которая определяется внешним воздействием, а и — магнитные моменты электронных орбит.

; — магнитная проницаемость.

.

Для разных веществ значение может принимать как положительные, так и отрицательные значения. В большинстве веществ собственные магнитные моменты атомов (молекул) не зависят друг от друга и хаотично расположены в пространстве. Если к такому веществу приложить внешнее поле, то собственный магнитный момент каждого атома стремится, как волчок, выровнять положение оси вращения вдоль силовых линий внешнего поля.

B_вне — индукция внешнего магнитного поля, Pm- собственный магнитный момент атома.

Изменение собственной оси вращения (собственного магнитного момента) относительно вектора магнитной индукции (внешнего поля) называется прецессией.

Собственный механический момент или количество движения Ls (спин)

Механические моменты электронов в атоме могут отличаться только направлением движения по орбите (вдоль и против часовой стрелки).

1. Если внешнее магнитное поле затрачивает энергию на прецессию, то её результирующее магнитное поле ослабляется. Такие вещества называют диа–магнетиками: .
2. В некоторых веществах внешнее магнитное поле не затрачивает энергию на прецессию, а разворачивает весь атом так, чтобы его собственное магнитное поле совпадало с внешним магнитным полем. Эти вещества -парамагнетики. Для них .

Парамагнетики

Стрелками укажем магнитные моменты отдельных атомов.

Ферромагнетики.

Для объяснения ферромагнетизма вводим понятие доменов. Домен — совокупность атомов с одинаковым направлением собственных магнитных полей. Подобные совокупности атомов требуют меньше энергии для образования доменов, т.е. энергетически более выгодны по сравнению с разрозненными атомами. В целом собственное магнитное поле вещества равно нулю. Под действием внешнего магнитного поля домены могут увеличиваться за счет других доменов вплоть до поглощения неориентированных доменов, то есть все пространство вещества заполняется доменами, ориентированными вдоль поля. При снятии внешнего поля обратной переориентации не происходит, так как это энергетически не выгодно. В этом случае магнитная восприимчивость составляет тысячи и десятки тысяч единиц. Оказывается, реакция вещества на воздействие внешнего магнитного поля носит нелинейный характер. Это определяется способностью собственных магнитных моментов переориентироваться во внешнем магнитном поле. Сначала идёт резкое изменение ориентации во внешнем магнитном поле, магнитные моменты ориентируются вдоль силовых линий магнитного поля. Дальнейшее увеличение магнитного поля не изменяет намагниченность, так как все магнитные моменты уже ориентированы вдоль поля. Зависимость результирующего магнитного поля в веществе в целом в зависимости от внешнего поля носит характер гистерезиса.

B₁ — остаточная индукция. H₁ — коэрцетивная сила.

B₁ — в веществе остается собственное магнитное поле без внешнего магнитного поля H₁ = 0, (так создаются постоянные магниты).

H₁ — внешнее поле, необходимое для снятия собственной намагниченности, B₁=0. Эта величина называется коэрцетивная сила.

Анализ петли гистерезиса см. в разделе “Сегнетоэлектрики”. Если коэрцетивная сила велика, то говорят, что ферромагнетик жёсткий, если мала — то мягкий.

Правило правой руки

Определение направления тока движущемся в магнитном поле проводника (одной стороны замкнутого витка проводников) наглядно демонстрирует правило правой руки.

Оно говорит о том, что правая ладонь, повернутая к полюсу N (силовые линии входят в ладонь), а большой палец, отклоненный на 90 градусов показывает направление движения проводника, то в замкнутом контуре (витке) магнитное поле индуцирует электрический ток, вектор движения которого указывают четыре пальца.

Это правило демонстрирует как изначально появились генераторы постоянного тока. Некая сила природы (вода, ветер) вращала замкнутый контур проводников в магнитном поле вырабатывая электроэнергию. Затем двигатели, получив электрический ток в постоянном магнитном поле преобразовывали его в механическое движение.

Правило правой руки справедливо и в случае катушек индуктивности. Движение внутри них магнитного сердечника приводит к появлению индукционных токов.

Правила буравчика и правой руки удачно демонстрируют взаимодействие электрического и магнитного полей. Они делают доступным понимание работы различных устройств в электротехнике практически всем, а не только ученым.

Что такое ЭДС индукции и когда возникает?

  Как подключить и настроить интернет на телевизоре?

Сила Лоренца и правило левой руки. Движение заряженных частиц в магнитном поле

Что такое датчик Холла: принцип работы, устройство и способы проверки на работоспособность

История открытия электричества

Что такое магнитный двигатель и как его сделать своими руками?

Что такое амперметр и как им проводить измерения?

Похожие записи:

Кд209 Монтаж водоотводных лотков — устройство и установка на примерах Расчет радиатора охлаждения воздуха Выполнение схемы электрической принципиальной и перечня элементов к ней Ограничители перенапряжения нелинейные (опн) Что такое реле контроля напряжения и для чего его используют в домах и квартирах