Связь со связанными количествами
Молярная и массовая восприимчивость
Для определения магнитной восприимчивости используются две другие меры:
восприимчивость к магнитной массе (также или , следует избегать сокращения ) в м 3 · кг -1 означает восприимчивость через плотностьχмасса{\ displaystyle \ chi _ {\ text {масса}}}χграмм{\ displaystyle \ chi _ {g}}χρ{\ displaystyle \ chi _ {\ rho}}χм{\ displaystyle \ chi _ {m}} ρ:{\ displaystyle \ rho:}
-
- χмассазнак равноχρзнак равноχ⋅Vм{\ displaystyle \ chi _ {\ text {mass}} = {\ frac {\ chi} {\ rho}} = \ chi \ cdot {\ frac {V} {m}}}
- с массой и объемом .м{\ displaystyle m} V{\ displaystyle V}
молярная магнитная восприимчивость в м 3 · моль -1 отличается использованием молекулярного веса или молярного объемом :χмоль{\ displaystyle \ chi _ {\ text {mol}}} М.{\ displaystyle M} Vм{\ Displaystyle V _ {\ mathrm {m}}}
-
- χмользнак равноМ.⋅χмассазнак равноМ.⋅χρзнак равноχ⋅мп⋅Vмзнак равноχ⋅Vпзнак равноχ⋅Vм{\ displaystyle \ chi _ {\ text {mol}} = M \ cdot \ chi _ {\ text {mass}} = M \ cdot {\ frac {\ chi} {\ rho}} = \ chi \ cdot {\ гидроразрыв {m} {n}} \ cdot {\ frac {V} {m}} = \ chi \ cdot {\ frac {V} {n}} = \ chi \ cdot V _ {\ mathrm {m}}}
- с количеством вещества .п{\ displaystyle n}
Магнитная проницаемость
Постоянная магнитная восприимчивость просто связана с относительной магнитной проницаемостью :
- χзнак равноμр-1{\ displaystyle \ chi = \ mu _ {r} -1}
Это следует из зависимости плотности магнитного потока от намагниченности и напряженности магнитного поля :
Б.{\ displaystyle B} М.{\ displaystyle M} ЧАС{\ displaystyle H}
-
- Б.знак равноμ⋅(ЧАС+М.)знак равноμ⋅(1+χ)⋅ЧАСзнак равноμ⋅μр⋅ЧАС{\ Displaystyle B = \ mu _ {0} \ cdot (H + M) = \ mu _ {0} \ cdot (1+ \ chi) \ cdot H = \ mu _ {0} \ cdot \ mu _ {r } \ cdot H}
с постоянной магнитного поля .
μ{\ displaystyle \ mu _ {0}}
Преобразование единиц СИ и СГС
Все приведенные выше определения относятся к Международной системе единиц (СИ), принятой в ЕС и Швейцарии . Так как проницаемость проницаемость вакуума определяется по- разному в системе гауссова CGS, коэффициент преобразования 4π:
- χГауссзнак равно14-йπ⋅χSI{\ displaystyle \ chi ^ {\ text {Gauss}} = {\ frac {1} {4 \ pi}} \ cdot \ chi ^ {\ text {SI}}}
Поэтому при использовании более старых табличных значений следует обращать внимание на используемую систему единиц. Например, восприимчивость воды при 20 ° C находится в системе Гаусса, что соответствует значению в СИ.
-7-е,19-е⋅10-7-е{\ displaystyle -7 {,} 19 \ cdot 10 ^ {- 7}}-9,04⋅10-Шестой{\ displaystyle -9 {,} 04 \ cdot 10 ^ {- 6}}. См
Также : Электромагнитные блоки
См. Также : Электромагнитные блоки
Системы единиц и историческое происхождение значения μ 0
В принципе, существует несколько систем уравнений, которые можно использовать для создания системы электрических величин и единиц. С конца 19 века фундаментальные определения текущих единиц были связаны с определениями единиц массы, длины и времени с использованием закона силы Ампера . Однако точный способ, которым это «официально» было сделано, много раз менялся по мере развития методов измерения и мышления по данной теме. Общая история единицы электрического тока и связанного с ней вопроса о том, как определить систему уравнений для описания электромагнитных явлений, очень сложна. Вкратце, основная причина, по которой μ имеет такое значение, заключается в следующем.
Силовой закон Ампера описывает экспериментально полученный факт, что для двух тонких, прямых, неподвижных, параллельных проводов на расстоянии r друг от друга, в каждом из которых протекает ток I , сила на единицу длины, F м / L , что один провод воздействует на другого в вакууме свободного пространства, было бы дано
FмL∝я2р.{\ displaystyle {\ frac {F _ {\ mathrm {m}}} {L}} \ propto {\ frac {I ^ {2}} {r}}. \;}
Запись константы пропорциональности в виде k m дает
FмLзнак равноkмя2р.{\ displaystyle {\ frac {F _ {\ mathrm {m}}} {L}} = k _ {\ mathrm {m}} {\ frac {I ^ {2}} {r}}. \;}
Необходимо выбрать форму k m, чтобы составить систему уравнений, а затем необходимо присвоить значение, чтобы определить единицу измерения тока.
В старой «электромагнитной (emu)» системе уравнений, определенной в конце 19 века, k m было выбрано как чистое число, 2, расстояние измерялось в сантиметрах, сила измерялась в дине единицы cgs , а токи определялись по этому уравнению были измерены в «электромагнитных единицах (emu) тока» (также называемых « abampere »). Практическая единица измерения, которую использовали электрики и инженеры, — ампер, — была определена как одна десятая электромагнитной единицы тока.
В другой системе, то «рационализировать метр-килограмм-вторых (rmks) система» (или в качестве альтернативы «метр-килограмм-вторых-амперные (MKSA) система»), к м записывается в виде μ /2 П , где μ постоянная измерительной системы, называемая «магнитной постоянной». Значение μ было выбрано таким, чтобы единица измерения тока rmks была равна по размеру амперу в системе эму: μ было определено как 4 π × 10 -7 Гн / м .
Исторически несколько разных систем (включая две описанные выше) использовались одновременно. В частности, физики и инженеры использовали разные системы, а физики использовали три разные системы для разных частей теории физики и четвертую другую систему (систему инженеров) для лабораторных экспериментов. В 1948 году организации по стандартизации приняли международные решения о принятии системы RMKS и связанного с ней набора электрических величин и единиц в качестве единой основной международной системы для описания электромагнитных явлений в Международной системе единиц .
Закон Ампера, как указано выше, описывает физическое свойство мира. Однако выбор формы k m и значения μ является полностью человеческим решением, принимаемым международными органами, состоящими из представителей национальных организаций по стандартизации всех стран-участниц. Параметр μ — это постоянная измерительной системы, а не физическая константа, которую можно измерить. Он ни в каком значимом смысле не описывает физическое свойство вакуума. Вот почему соответствующие организации по стандартизации предпочитают название «магнитная постоянная», а не любое название, которое несет скрытый и вводящий в заблуждение смысл, что μ описывает какое-то физическое свойство.
значение
Значение постоянной магнитного поля равнялось 2019 г. по прежнему определению набора единиц ампер . Согласно этому определению, два параллельных бесконечно длинных проводника на расстоянии одного метра в вакууме, по которым протекает электрический ток с током в 1 ампер, оказывают друг на друга силу 2 · 10 -7 Ньютонов на метр длина проводника . Из закона силы Ампера так, чтобы точное значение постоянной магнитного поля, за которым следует
- μзнак равно4-йπ⋅10-7-еNА.алт2знак равно1,25663706214-е…⋅10-6-еNА.алт2{\ displaystyle \ mu _ {0} = 4 \ pi \ cdot 10 ^ {- 7} \ mathrm {\ frac {N} {A_ {alt} ^ {2}}} = 1 {,} 256 \, 637 \ , 062 \, 14 \ ldots \ cdot 10 ^ {- 6} {\ frac {\ mathrm {N}} {\ mathrm {A_ {alt} ^ {2}}}}}.
В результате решенных на 26 — й Генеральной конференции по мерам и весам (CGPM), Ампер был определен на основе элементарного заряда е и определения второй после 20 мая 2019 года . В результате постоянная магнитного поля стала переменной, которую нужно было определять экспериментально и допускать погрешность измерения. Значение элементарного заряда, которое теперь определяется по определению, было выбрано таким образом, чтобы ампер и, следовательно, также значение μ оставались неизменными, насколько это возможно. На момент вступления в силу 20 мая 2019 г. стоимость составляла
- μзнак равно1,25663706212-е(19-е)⋅10-6-еNА.2{\ displaystyle \ mu _ {0} = 1 {,} 256 \, 637 \, 062 \, 12 (19) \ cdot 10 ^ {- 6} {\ frac {\ mathrm {N}} {\ mathrm {A } ^ {2}}}}
указано. При относительной погрешности измерения 1,5 · 10 -10 это значение с тех пор общепризнано как наиболее точное доступное значение.
Магнитная восприимчивость некоторых материалов
| материал | χ{\ displaystyle \ chi} | χмОл{\ displaystyle \ chi _ {\ mathrm {mol}}} | χмаss{\ displaystyle \ chi _ {\ mathrm {масса}}} |
|---|---|---|---|
| пылесос | |||
| гелий | -0.0238е-9 м 3 моль -1 | -5.93е-9 м 3 кг −1 | |
| ксенон | -0.57 годе-9 м 3 моль -1 | -4-й.35 годе-9 м 3 кг −1 | |
| кислород | 43 годе-9 м 3 моль -1 | 2 690е-9 м 3 кг −1 | |
| вода | -9.035е-Шестой | -0.163е-9 м 3 моль -1 | -9.05е-9 м 3 кг −1 |
| алмаз | -20-ее-Шестой | -0.069е-9 м 3 моль -1 | -5.8-ее-9 м 3 кг −1 |
| Графит (вертикальный) | -45е-Шестой | -2.4-йе-9 м 3 моль -1 | -200е-9 м 3 кг −1 |
| Графит (параллельный) | -85е-Шестой | -0.45е-9 м 3 моль -1 | -38е-9 м 3 кг −1 |
| алюминий | 21 годе-Шестой | 0.22-ее-9 м 3 моль -1 | 7-е.9е-9 м 3 кг −1 |
| серебро | -24е-Шестой | -0.238е-9 м 3 моль -1 | -2.20-ее-9 м 3 кг −1 |
| Висмут | -166е-Шестой | -3.55е-9 м 3 моль -1 | -17-е.0е-9 м 3 кг −1 |
Восприимчивость лишь незначительно зависит от температуры, но часто сильно зависит от физического состояния, кристаллической системы и направления кристаллической решетки. Большая анизотропия может наблюдаться, например, у пиролитически осажденного графита.
Магнитная проницаемость вещества
Допустим, что вещество однородно и им заполнено все пространство, где имеется магнитное поле. Обозначим, как $L_0\ $индуктивность контура в вакууме, $L$ — индуктивность того же контура в веществе, в котором присутствует магнитное поле. Тогда отношение:
называется относительной магнитной проницаемостью (или просто магнитной проницаемостью) вещества.
Магнитная проницаемость — это физическая величина, зависящая от рода вещества и его состояния, характеризующая магнитные свойства вещества.
Вводится магнитная проницаемость аналогично диэлектрической проницаемости ($\varepsilon $). В таком случае параметр $\mu $, есть отношение абсолютных магнитных проницаемостей исследуемого вещества и вакуума (${\mu }_0$).
Параметр $\mu $ — это безразмерная величина. При этом абсолютная магнитная проницаемость (${\mu }_a$) равна:
Единицей измерения абсолютной магнитной проницаемости является:
1 $\frac{Гн}{м}$ — это магнитная проницаемость вещества, в которой при напряженности магнитного поля равной 1 $\frac{А}{м}$ создается магнитная индукция 1 Тл.
Вещество оказывает влияние на индуктивность контура, это говорит, о том что при изменении среды изменяется магнитный поток, который пронизывает контур, следовательно, изменяется величина магнитной индукции поля. Если магнитная проницаемость вещества равна $\mu $, то при той же силе тока в контуре индукция в $\mu $ раз больше, чем в вакууме:
Эмпирически получено, что магнитная проницаемость в большинстве случаев $\mu $ мало отличается от единицы. Эта величина может быть больше и меньше единицы. Вещества, которые имеют $\mu >1,$ называют парамагнетиками. При $\mu
У ферромагнитных веществ магнитная проницаемость достигает больших значений (много больших, чем у пара и диа — магнетиков). Кроме этого магнитная проницаемость ферромагнетиков зависит от напряженности внешнего магнитного поля.
Магнитная проницаемость вещества связана с магнитной восприимчивостью соотношением:
Магнитные линии и магнитный поток
Вокруг магнита экспериментальным путем были обнаружены магнитные силовые линии. Эти магнитные линии создают так называемое магнитное поле.
Как вы могли заметить на рисунке, концентрация магнитных силовых линий на самых краях магнита намного больше, чем в его середине. Это говорит о том, что магнитное поле является более сильным именно на краях магнита, а в его середине практически равна нулю. Направлением магнитных силовых линий считается направление от севера к югу.
Ошибочно считать, что магнитные силовые линии начинают свое движение от северного полюса и заканчивают свой век на южном. Это не так. Магнитные линии – они замкнуты и непрерывны. В магните это будет выглядеть примерно так.
Если приблизить два разноименных полюса, то произойдет притягивание магнитов
Если же приблизить одноименными полюсами, то произойдет их отталкивание
Итак, ниже важные свойства магнитных силовых линий.
- Магнитные линии не поддаются гравитации.
- Никогда не пересекаются между собой.
- Всегда образуют замкнутые петли.
- Имеют определенное направление с севера на юг.
- Чем больше концентрация силовых линий, тем сильнее магнитное поле.
- Слабая концентрация силовых линий указывает на слабое магнитное поле.
Магнитные силовые линии, которые образуют магнитное поле, называют также магнитным потоком.
Итак, давайте рассмотрим два рисунка и ответим себе на вопрос, где плотность магнитного потока будет больше? На рисунке “а” или на рисунке “б”?
Видим, что на рисунке “а” мало силовых магнитных линий, а на рисунке “б” их концентрация намного больше. Отсюда можно сделать вывод, что плотность магнитного потока на рисунке “б” больше, чем на рисунке “а”.
В физике формула магнитного потока записывается как
где
Ф – магнитный поток, Вебер
В – плотность магнитного потока, Тесла
а – угол между перпендикуляром n (чаще его зовут нормалью) и плоскостью S, в градусах
S – площадь, через которую проходит магнитный поток, м2
Что же такое 1 Вебер? Один вебер – это магнитный поток, который создается полем индукцией 1 Тесла через площадку 1м2 расположенной перпендикулярно направлению магнитного поля.
Как связана индукция и напряженность магнитного поля?
Магнетиком называется вещество, которое под действием магнитного поля способно намагничиваться (или как говорят физики приобретать магнитный момент). Магнетиками являются практически все вещества. Намагничивание веществ объясняется тем, что в веществах присутствуют свои собственные микроскопические магнитные поля, которые создаются вращением электронов по своим орбитам. Когда внешнее магнитное поле отсутствует, то микроскопические поля расположены произвольным образом, а под воздействием внешнего магнитного поля соответствующим образом ориентируются.
Для характеристики намагничивания различных веществ используют так называемый вектор намагничивания J.
Таким образом, под действием внешнего магнитного поля с магнитной индукцией В, магнетик намагничивается и создает свое магнитное поле с магнитной индукцией В’. В итоге общая индукция В будет состоять из двух слагаемых
Тут возникает проблема вычисления магнитной индукции намагниченного вещества В’, для решения которой необходимо считать электронные микротоки всего вещества, что практически нереально.
Альтернативой данного решения есть ввод вспомогательных параметров, а именно напряженность магнитного поля Н и магнитная восприимчивость χ. Напряженность связывает магнитную индукцию В и намагничивание вещества J следующим выражением
где В – магнитная индукция,
μ – магнитная постоянная, μ = 4π*10-7 Гн/м.
В то же время вектор намагничивания J связан с напряженность магнитного поля В параметром, характеризующим магнитные свойства вещества и называемым магнитной восприимчивостью χ
где J – вектор намагничивания вещества,
μr – относительная магнитная проницаемость вещества.
Однако наиболее часто для характеристики магнитных свойств веществ используют относительную магнитную проницаемость μr.
Таким образом, связь между напряженностью и магнитной индукцией будет иметь следующий вид
где μ – магнитная постоянная, μ = 4π*10-7 Гн/м,
μr – относительная магнитная проницаемость вещества.
Так как намагничивание вакуума равна нулю (J = 0), то напряженность магнитного поля в вакууме будет равна
Отсюда можно вывести выражения напряженности для магнитного поля, создаваемого прямым проводом с током:
где I – ток протекающий по проводнику,
b – расстояние от центра провода до точки, в которой считается напряженность магнитного поля.
Как видно из данного выражения единицей измерения напряженности является ампер на метр (А/м) или эрстед (Э)
Таким образом, магнитная индукция В и напряженность Н являются основными характеристиками магнитного поля, а магнитная проницаемость μr – магнитной характеристикой вещества.
Проявление магнитного поля
Магнитное поле проявляется в воздействии на магнитные моменты частиц и тел, на движущиеся заряженные частицы (или проводники с током). Сила, действующая на движущуюся в магнитном поле электрически заряженную частицу, называется силой Лоренца, которая всегда направлена перпендикулярно к векторам v и B. Она пропорциональна заряду частицы q, составляющей скорости v, перпендикулярной направлению вектора магнитного поля B, и величине индукции магнитного поля B.
В Международной системе единиц (СИ) сила Лоренца выражается так:
в системе единиц СГС:
где квадратными скобками обозначено векторное произведение.
Также (вследствие действия силы Лоренца на движущиеся по проводнику заряженные частицы) магнитное поле действует на проводник с током. Сила, действующая на проводник с током называется силой Ампера. Эта сила складывается из сил, действующих на отдельные движущиеся внутри проводника заряды.
Взаимодействие двух магнитов
Одно из наиболее часто встречающихся в обычной жизни проявлений магнитного поля — взаимодействие двух магнитов: одинаковые полюса отталкиваются, противоположные притягиваются. Представляется заманчивым описать взаимодействие между магнитами как взаимодействие между двумя монополями, и с формальной точки зрения эта идея вполне реализуема и часто весьма удобна, а значит практически полезна (в расчётах); однако детальный анализ показывает, что на самом деле это не полностью правильное описание явления (наиболее очевидным вопросом, не получающим объяснения в рамках такой модели, является вопрос о том, почему монополи никогда не могут быть разделены, то есть почему эксперимент показывает, что никакое изолированное тело на самом деле не обладает магнитным зарядом; кроме того, слабостью модели является то, что она неприменима к магнитному полю, создаваемому макроскопическим током, а значит, если не рассматривать её как чисто формальный приём, приводит лишь к усложнению теории в фундаментальном смысле).
Правильнее будет сказать, что на магнитный диполь, помещённый в неоднородное поле, действует сила, которая стремится повернуть его так, чтобы магнитный момент диполя был сонаправлен с магнитным полем. Но никакой магнит не испытывает действия (суммарной) силы со стороны однородного магнитного поля. Сила, действующая на магнитный диполь с магнитным моментом m выражается по формуле:
Сила, действующая на магнит (не являющийся одиночным точечным диполем) со стороны неоднородного магнитного поля, может быть определена суммированием всех сил (определяемых данной формулой), действующих на элементарные диполи, составляющие магнит.
Впрочем, возможен подход, сводящий взаимодействие магнитов к силе Ампера, а сама формула выше для силы, действующей на магнитный диполь, тоже может быть получена, исходя из силы Ампера.
Явление электромагнитной индукции
Основная статья: Электромагнитная индукция
Если поток вектора магнитной индукции через замкнутый контур меняется во времени, в этом контуре возникает ЭДС электромагнитной индукции, порождаемая (в случае неподвижного контура) вихревым электрическим полем, возникающим вследствие изменения магнитного поля со временем (в случае неизменного со временем магнитного поля и изменения потока из-за движения контура-проводника такая ЭДС возникает посредством действия силы Лоренца).
Определение
Восприимчивость к объему
Магнитная восприимчивость — это безразмерная константа пропорциональности, которая указывает степень намагничивания материала в ответ на приложенное магнитное поле . Связанный термин — намагничиваемость , соотношение между магнитным моментом и плотностью магнитного потока . Тесно связанным параметром является проницаемость , которая выражает общую намагниченность материала и объема.
Объем магнитная восприимчивость , представленное символом х V (часто просто χ , иногда χ м — магнитные, чтобы отличить от электрической восприимчивости ), определяются в Международной системе единиц — в других системах могут существовать дополнительные константы — по следующие отношения:
- Mзнак равноχvЧАС.{\ displaystyle \ mathbf {M} = \ chi _ {\ text {v}} \ mathbf {H}.}
Здесь
- M — намагниченность материала ( магнитный дипольный момент на единицу объема) в единицах ампер на метр, а
- H — напряженность магнитного поля , также в амперах на метр.
Следовательно, χ v — безразмерная величина .
Использование единиц СИ , то магнитная индукция В связана с H соотношением
- B знак равно μ(ЧАС+M) знак равно μ(1+χv)ЧАС знак равно μЧАС{\ displaystyle \ mathbf {B} \ = \ \ mu _ {0} \ left (\ mathbf {H} + \ mathbf {M} \ right) \ = \ \ mu _ {0} \ left (1+ \ chi _ {\ text {v}} \ right) \ mathbf {H} \ = \ \ mu \ mathbf {H}}
где μ — проницаемость вакуума (см. таблицу физических констант ), а (1 + χ v ) — материала. Таким образом, объемная магнитная восприимчивость χ v и магнитная проницаемость μ связаны следующей формулой:
- μзнак равноμ(1+χv).{\ displaystyle \ mu = \ mu _ {0} \ left (1+ \ chi _ {\ text {v}} \ right).}
Иногда вспомогательная величина, называемая интенсивностью намагничивания I (также называемая магнитной поляризацией J ), в единицах тесла определяется как
- язнак равноμM.{\ displaystyle \ mathbf {I} = \ mu _ {0} \ mathbf {M}.}
Это позволяет альтернативное описание всех явлений намагниченности в терминах величин I и B , в отличие от обычно используемого M и H .
Молярная восприимчивость и массовая восприимчивость
Существуют два других показателя восприимчивости, молярная магнитная восприимчивость ( χ m ) с единицей измерения м 3 / моль и массовая магнитная восприимчивость ( χ ρ ) с единицей измерения м 3 / кг, которые определены ниже, где ρ — плотность с единицей измерения кг / м 3, а M — молярная масса в кг / моль:
- χρзнак равноχvρ;χмзнак равноMχρзнак равноMρχv.{\ displaystyle {\ begin {align} \ chi _ {\ rho} & = {\ frac {\ chi _ {\ text {v}}} {\ rho}}; \\\ chi _ {\ text {m} } & = M \ chi _ {\ rho} = {\ frac {M} {\ rho}} \ chi _ {\ text {v}}. \ End {align}}}
В единицах СГС
Приведенные выше определения соответствуют Международной системе количеств (ISQ), на которой основана SI . Однако во многих таблицах магнитной восприимчивости приведены значения соответствующих величин системы CGS (более конкретно, , сокращение от электромагнитных единиц, или Gaussian-CGS ; в данном контексте они одинаковы). Величины, характеризующие проницаемость свободного пространства для каждой системы, имеют разные определяющие уравнения:
- BCGSзнак равноЧАСCGS+4πMCGSзнак равно(1+4πχvCGS)ЧАСCGS.{\ displaystyle \ mathbf {B} ^ {\ text {CGS}} = \ mathbf {H} ^ {\ text {CGS}} + 4 \ pi \ mathbf {M} ^ {\ text {CGS}} = \ left (1 + 4 \ pi \ chi _ {\ text {v}} ^ {\ text {CGS}} \ right) \ mathbf {H} ^ {\ text {CGS}}.}
Соответствующие восприимчивости CGS умножаются на 4 π, чтобы получить соответствующие величины ISQ (часто называемые величинами SI) с теми же единицами:
- χмSIзнак равно4πχмCGS{\ displaystyle \ chi _ {\ text {m}} ^ {\ text {SI}} = 4 \ pi \ chi _ {\ text {m}} ^ {\ text {CGS}}}
- χρSIзнак равно4πχρCGS{\ displaystyle \ chi _ {\ text {ρ}} ^ {\ text {SI}} = 4 \ pi \ chi _ {\ text {ρ}} ^ {\ text {CGS}}}
- χvSIзнак равно4πχvCGS{\ displaystyle \ chi _ {\ text {v}} ^ {\ text {SI}} = 4 \ pi \ chi _ {\ text {v}} ^ {\ text {CGS}}}
Например, объемная магнитная восприимчивость воды в ХСП при 20 ° C равна 7,19 × 10 −7 , что составляет9,04 × 10 −6 согласно условию СИ , обе величины безразмерны. В то время как для большинства электромагнитных величин, к какой системе величин они принадлежат, можно понять несовместимость их единиц, это неверно для величин восприимчивости.
В физике принято рассматривать массовую восприимчивость ХСП в единицах см 3 / г или ЭМЕ / г⋅Э -1 , а молярную восприимчивость ХГС в единицах см 3 / моль или ЭМЕ / моль⋅Э -1 .
Свойства[править | править код]
Магнитная проницаемость в СИ связана с магнитной восприимчивостью χ соотношением:
- μ=1+χ{\displaystyle \mu =1+\chi },
а в гауссовой системе аналогичное соотношение выглядит как
- μ=1+4πχ{\displaystyle \mu =1+4\pi \chi }.
Вообще говоря, магнитная проницаемость зависит как от свойств вещества, так и от величины и направления магнитного поля для анизотропных веществ (и, кроме того, от температуры, давления и т. д.).
Также она зависит от скорости изменения поля со временем, в частности, для синусоидального изменения поля — зависит от частоты этого колебания (в этом случае для описания намагничивания вводят комплексную магнитную проницаемость, чтобы описать влияние вещества на сдвиг фазы B относительно H). При достаточно низких частотах — небольшой быстроте изменения поля, её можно обычно считать в этом смысле независимой от частоты.
Схематический график зависимости ‘B’ от ‘H’ (кривая намагничивания) для ферромагнетиков, парамагнетиков и диамагнетиков, а также для вакуума, иллюстрирующий различие магнитной проницаемости (представляющей собою наклон графика) для: ферромагнетиков (μf), парамагнетиков (μp), вакуума(μ) и диамагнетиков (μd)
Кривая намагничивания для ферромагнетиков (и ферримагнетиков) и соответствующий ей график магнитной проницаемости
Магнитная проницаемость сильно зависит от величины поля для нелинейных по магнитной восприимчивости сред (типичный пример — ферромагнетики, для которых характерен магнитный гистерезис). Для таких сред магнитная проницаемость, как независящее от поля число, может указываться приближенно, в линейном приближении.
Для неферромагнитных сред линейное приближение μ={\displaystyle \mu =}const достаточно хорошо выполняется для широкого диапазона изменения величины поля.
Принцип работы.
Схема магнитометра может сильно отличаться, но в любом случае он работает по одной и той же методике. Магнитное поле может быть охарактеризовано следующим:
- вектор напряженности;
- горизонтальная составляющая напряженности;
- магнитное склонение;
- магнитное наклонение.


Но есть еще одна важная характеристика магнитного поля – магнитная индукция. По направлению ее вектора определяется направление силы, воздействующей на северный полюс магнита. Чтобы понять, как все это работает, полезно рассмотреть устройство магнитометрического датчика HMC5883L от Honeywell. Меняющийся коэффициент усиления влияет на восприимчивость датчика. Для считывания данных предусмотрено 12 регистров с разрядностью 8.
Регистр режима задает основной сценарий действия: непрерывное измерение либо разовый замер и переход в режим ожидания. Если запрос идет не программно, а аппаратно, используется дублирование данных через вывод DRDY. Но не все так просто – требуется учитывать не только показания датчиков, но и воздействия на них различных помех.
Если проигнорировать этот момент, может оказаться так, что модуль сбился и измеряет совсем не то, что нужно.

Предположим, требуется произвести измерения удельной намагниченности насыщения. Образец, который нужно исследовать, и постоянный магнит крепятся на тонком стержне, соединенном с вибрационным узлом. Колебания стержня могут происходить с различной частотой, но в любом случае под углом 90 градусов к полю, создаваемому электромагнитом. Радиотехнические компоненты системы призваны усиливать, очищать и эффективно обрабатывать сигнал. Когда постоянный магнит и образец колеблются, появляется электродвижущая сила в особых катушках. Сами катушки позиционируют по отношению к постоянному магниту так, чтобы на их положение не влияли вибрационные колебания.
Но описанное устройство, как нетрудно понять по некоторым моментам, может применяться преимущественно в лабораторных условиях. Возможности его использования «в поле» существенно ограничены. Для полевых измерений предназначены уже совершенно другие магнитометры, которые не требуют изготовления и выделения образцов. Как именно работает такая техника – коммерческая тайна производителей
В любом случае, нужно ли производить измерения остаточной намагниченности или делать что-то еще, важно знать алгоритм калибровки методом наименьших квадратов


Максимально упрощенно излагая суть этого метода (основанного на высшей математике), можно указать, что он подразумевает подбор функции, дающей значения, максимально близкие к полученным по итогам эксперимента. Сумма квадратов отклонений во всех критических важных точках должна быть как можно меньшей, в идеале – сведенной к нулю.
Обязательным условием для применения такого алгоритма является знание вектора магнитного поля земли. Если же вернуться к математической стороне дела, то можно сказать, что тут нужны линейные преобразования матриц в трехмерном пространстве. А отсюда следует, что придется использовать показания по трем осям сразу.
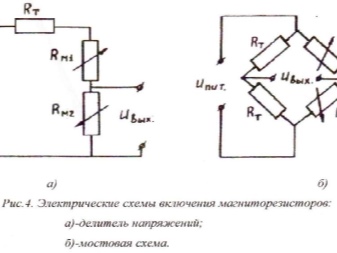
Немного отстранившись от всей этой зауми, можно разобраться, как действует магнитометр на основе тонкопленочных магниторезисторов. Такая техника выпускается ведущими иностранными фирмами. Магниторезисторы обычно размещают на одной кремниевой подложке и соединяют мостовым способом.
Поскольку сопротивление резисторов сложно подогнать при производстве, нельзя игнорировать напряжение смещения. Параметры датчиков очень сильно зависят от фактической температуры.