Конструкция трансформатора тока
В реальном мире у сигнальной жилы есть ненулевое пассивное сопротивление и для создания в ней тока необходимо ненулевое значение ЭДС индукции, а значит магнитный поток силовой обмотки должен быть скомпенсирован не полностью. Чтобы ток в сигнальной обмотке был максимально близок к идеальному, нужно максимизировать отношение напряжения разомкнутой обмотки к реальному падению напряжения, необходимому для создания этого тока. Этого можно добиться разными способами:
-
снижением целевого падения напряжения на сигнальной обмотке
-
увеличением числа витков силовой обмотки
-
увеличением числа витков сигнальной обмотки
-
увеличением индуктивности каждого витка
Минимизировать напряжение на сигнальной обмотке можно за счёт более чувствительной схемы измерения тока. В самом простом случае ток преобразуется в напряжение на шунтирующем резисторе и падение напряжения определяется диапазоном детектируемых токов и характеристиками аналогового входа микроконтроллера.
Существенно увеличить число витков в силовой обмотке сложно, т.к. через неё подключается нагрузка, а значит у неё должно быть и сечение достаточно большое, и изоляция надёжная. А вот в сигнальной обмотке число витков можно увеличить весьма значительно, причём поскольку ток в сигнальной обмотке обратно пропорционален числу витков в ней, сечение провода также можно существенно уменьшить. Именно поэтому в токовых трансформаторах в сигнальной обмотке обычно значительно больше витков, чем в силовой.
Индуктивность каждого витка можно очень сильно увеличить с помощью ферромагнитного магнитопровода. Обычная электротехническая сталь увеличивает магнитную индукцию в несколько тысяч раз, а также концентрирует магнитное поле внутри магнитопровода, обеспечивая полноту прохождения магнитного потока через витки сигнальной обмотки. Например один виток на ферритовом кольце имеет индуктивность около 3 мкГн, что в 12 раз больше, чем те 0.25 мкГн, которые у нас получились для витка в мотке кабеля намного больших размеров.
Наличие магнитопровода в конструкции трансформатора приводит и к некоторым ограничениям:
-
Напряжённость поля внутри сердечника ограничена эффектом магнитного насыщения, т.е. чем больше измеряемый ток — тем больше должно быть сечение сердечника, чтобы распределить магнитное поле по большей площади.
-
Сердечник должен успевать перемагничиваться вслед за изменением магнитного поля силовой обмотке, т.е. частота изменения измеряемого тока ограничена характеристиками материала сердечника.
-
При перемагничивании сердечника выделяется тепло, что ограничивает произведение частоты изменения тока на величину магнитного поля.
Все эти ограничения однако больше влияют на конструкцию силовых трансформаторов, а для измерительного трансформатора достаточно легко можно обеспечить очень большой запас по каждому из этих ограничений.
Применение закона Ома на практике
На практике часто приходится определять не силу тока I, а величину сопротивления R. Преобразовав формулу Закона Ома, можно рассчитать величину сопротивления R, зная протекающий ток I и величину напряжения U.
| Онлайн калькулятор для определения величины сопротивления | |
|---|---|
| Напряжение, В: | |
| Величина тока, А: | |
Величину сопротивления может понадобится рассчитать, например, при изготовлении блока нагрузок для проверки блока питания компьютера. На корпусе блока питания компьютера обычно есть табличка, в которой приведен максимальный ток нагрузки по каждому напряжению. Достаточно в поля калькулятора ввести данные величины напряжения и максимальный ток нагрузки и в результате вычисления получим величину сопротивления нагрузки для данного напряжения. Например, для напряжения +5 В при максимальной величине тока 20 А, сопротивление нагрузки составит 0,25 Ом.
Принцип работы трансформатора.
Принцип работы трансформатора основан на явлении электромагнитной индукции.
Если на первичную обмотку подать переменное напряжение U1, то по виткам обмотки потечет переменный ток Io, который вокруг обмотки и в магнитопроводе создаст переменное магнитное поле. Магнитное поле образует магнитный поток Фo, который проходя по магнитопроводу пересекает витки первичной и вторичной обмоток и индуцирует (наводит) в них переменные ЭДС – е1 и е2. И если к выводам вторичной обмотки подключить вольтметр, то он покажет наличие выходного напряжения U2, которое будет приблизительно равно наведенной ЭДС е2.
При подключении к вторичной обмотке нагрузки, например, лампы накаливания, в первичной обмотке возникает ток I1, образующий в магнитопроводе переменный магнитный поток Ф1 изменяющийся с той же частотой, что и ток I1. Под воздействием переменного магнитного потока в цепи вторичной обмотки возникает ток I2, создающий в свою очередь противодействующий согласно закону Ленца магнитный поток Ф2, стремящийся размагнитить порождающий его магнитный поток.
В результате размагничивающего действия потока Ф2 в магнитопроводе устанавливается магнитный поток Фo равный разности потоков Ф1 и Ф2 и являющийся частью потока Ф1, т.е.
Результирующий магнитный поток Фo обеспечивает передачу магнитной энергии из первичной обмотки во вторичную и наводит во вторичной обмотке электродвижущую силу е2, под воздействием которой во вторичной цепи течет ток I2. Именно благодаря наличию магнитного потока Фo и существует ток I2, который будет тем больше, чем больше Фo. Но и в то же время чем больше ток I2, тем больше противодействующий поток Ф2 и, следовательно, меньше Фo.
Из сказанного следует, что при определенных значениях магнитного потока Ф1 и сопротивлений вторичной обмотки и нагрузки устанавливаются соответствующие значения ЭДС е2, тока I2 и потока Ф2, обеспечивающие равновесие магнитных потоков в магнитопроводе, выражаемое формулой приведенной выше.
Таким образом, разность потоков Ф1 и Ф2 не может быть равна нулю, так как в этом случае отсутствовал бы основной поток Фo, а без него не мог бы существовать поток Ф2 и ток I2. Следовательно, магнитный поток Ф1, создаваемый первичным током I1, всегда больше магнитного потока Ф2, создаваемого вторичным током I2.
Величина магнитного потока зависит от создающего его тока и от числа витков обмотки, по которой он проходит.
Напряжение вторичной обмотки зависит от соотношения чисел витков в обмотках. При одинаковом числе витков напряжение на вторичной обмотке будет приблизительно равно напряжению, подаваемому на первичную обмотку, и такой трансформатор называют разделительным.
Если вторичная обмотка содержит больше витков, чем первичная, то развиваемое в ней напряжение будет больше напряжения, подаваемого на первичную обмотку, и такой трансформатор называют повышающим.
Если же вторичная обмотка содержит меньшее число витков, чем первичная, то и напряжение ее будет меньше, чем напряжение подаваемое на первичную обмотку, и такой трансформатор называют понижающим.
Следовательно. Путем подбора числа витков обмоток, при заданном входном напряжении U1 получают желаемое выходное напряжение U2. Для этого пользуются специальными методиками по расчету параметров трансформаторов, с помощью которых производится расчет обмоток, выбирается сечение проводов, определяются числа витков, а также толщина и тип магнитопровода.
Трансформатор может работать только в цепях переменного тока. Если его первичную обмотку подключить к источнику постоянного тока, то в магнитопроводе образуется магнитный поток постоянный во времени, по величине и направлению. В этом случае в первичной и вторичной обмотках не будет индуцироваться переменное напряжение, а следовательно, не будет передаваться электрическая энергия из первичной цепи во вторичную. Однако если в первичной обмотке трансформатора будет течь пульсирующий ток, то во вторичной обмотке будет индуцироваться переменное напряжение частота которого будет равна частоте пульсации тока в первичной обмотке.
Закон Ома для переменного тока
Мы с вами знаем формулировку закона Ома для цепей постоянного тока, которая гласит, что ток в такой цепи прямо пропорционален напряжению на элементе цепи и обратно пропорционален сопротивлению этого элемента постоянному току, протекающему через него.
Однако при изучении цепей переменного тока стало известно, что оказывается кроме элементов цепей с активным сопротивлением, есть элементы цепи с так называемым реактивным сопротивлением, то есть индуктивности и емкости (катушки и конденсаторы).
В цепи, содержащей только активное сопротивление, фаза тока всегда совпадает с фазой напряжения (рис 1.), т. е. сдвиг фаз тока и напряжения в цепи с чисто активным сопротивлением равен нулю.
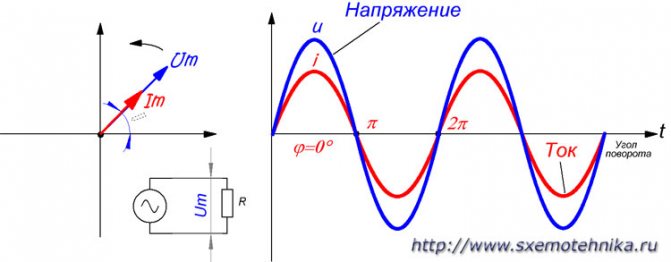
Рисунок 1. Напряжение и ток в цепи с чисто активным сопротивлением. Сдвиг фаз между током и напряжение в цепи переменного тока с чисто активным сопротивлением всегда равен нулю
Отсюда следует, что угол между радиус-векторами тока и напряжения также равен нулю.
Тогда, падение напряжения на активном сопротивлении определяется по формуле:
| (1) |
где, U-напряжение на элементе цепи,
I – ток через элемент цепи
R – активное сопротивление элемента
Формула (1) применима как для амплитудных, так и для эффективных значений тока и напряжения:
где, Um-амплитудное значение напряжения на элементе цепи,
Im – амплитудное значение тока через элемент цепи
R – активное сопротивление элемента
В цепи, содержащей чисто реактивное сопротивление — индуктивное или емкостное, — фазы тока и напряжения сдвинуты друг относительно друга на четверть периода, причем в чисто индуктивной цепи фаза тока отстает от фазы напряжения (рис. 2), а в чисто емкостной цепи фаза тока опережает фазу напряжения (рис. 3).
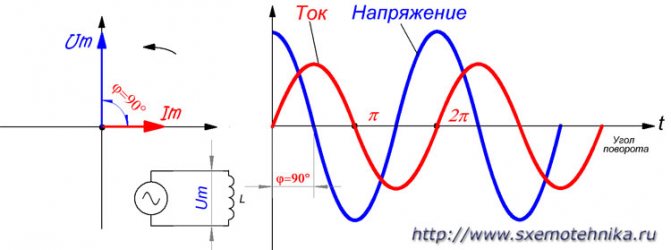
Рисунок 2. Напряжение и ток в цепи с чисто индуктивным сопротивлением. Фаза тока отстает от фазы напряжения на 90 градусов.
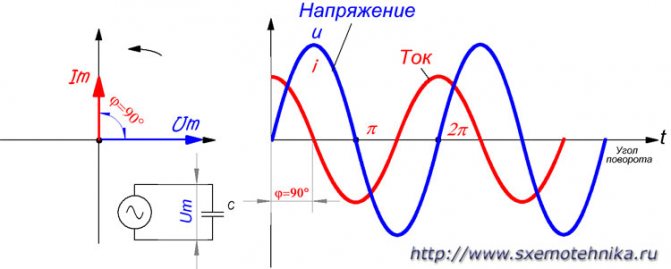
Рисунок 3. Напряжение и ток в цепи с чисто емкостным сопротивлением. Фаза тока опережает фазу напряжения на угол 90 градусов.
Отсюда следует, что в чисто реактивной цепи угол между радиус-векторами тока и напряжения всегда равен 90°, причем в чисто индуктивной цепи радиус-вектор тока при вращении движется позади радиус-вектора напряжения, а в чисто емкостной цепи он движется впереди радиус-вектора напряжения.
Падения напряжения на индуктивном и емкостном сопротивлениях определяются соответственно по формулам:
где — UL-падение напряжение на чисто индуктивном сопротивлении ;
UС—падение напряжения на чисто емкостном сопротивлении;
I— значение тока в через реактивное сопротивление;
L— индуктивность реактивного элемента;
C— емкость реактивного элемента;
ω— циклическая частота.
Эти формулы применимы как для амплитудных, так и для эффективных значений тока и напряжения синусоидальной формы. Однако здесь следует отметить, что они ни в коем случае не применимы для мгновенных значений тока и напряжения, а также и для несинусоидальных токов.
Приведенные выше формулы являются частными случаями закона Ома для переменного тока.
Следовательно, полный закон Ома для переменного тока будет иметь вид:
Где Z – полное сопротивление цепи переменного тока.
Теперь остается только вычистислить полное сопротивление цепи, а оно зависит непосредсвенно от какие активные и реактивные элементы присутсвуют в цепи и как они соединены.
Эффективные (RMS) значения
Среднеквадратическим (RMS), или эффективным значением является значение напряжения или тока, при котором на нагрузке рассеивается та же мощность, что и при постоянном напряжении или токе. При переменном напряжении с эффективным значением 230В будет выделяться такое же количество тепла на нагрузке, как и при постоянном напряжении 230В. Действующее значение относится только к выделению тепла на резистивной нагрузке. Для примера, значение RMS тока полезно для измерения напряжения под нагрузкой в проводе (= резистивная), но не для измерения зарядного тока батареи или конденсатора (= поток электронов).
Среднеквадратическое значение
RMS является аббревиатурой от Root Mean Square, что буквально переводится как среднеквадратическое значение.
Над напряжением или током, как функциями времени, для вычисления значения RMS последовательно проводятся три математические операции: возведение в квадрат, усреднение и извлечение квадратного корня. Почему так?
Мощность, выделяемая на резисторе, подключенным к источнику напряжения:
(12)
Для мгновенных мощности и напряжения:
(13)
Вычисление средней мощности как функции времени показано в (10). можем подстваить из (13):
(14)
Так как — константа, то ее можно вынести за интеграл:
(15)
Перенеся напряжение в уравнении (12) в левую часть, мы можем расчитать напряжение по средней мощности и сопротивлению:
(16)
Затем, вычисленную среднюю мощность из (15), подставим в уравнение (16):
(17)
Сократив значения сопротивлений , получим:
(18)
Хорошо видно, что это уравнение состоит из трех частей: квадрата , среднего и квадратного корня.
В приведенных выше выкладках вычислялось значение напряжения на резисторе. Аналогично можно сделать и для тока через резистор:
(19)
Большинство мультиметров не может вычислить эффективное значение измеряемого напряжения. Чтобы узнать среднеквадратическое значение, обычно необходим специальный прибор.
На рисунке ниже показано, как вычисляет измеряемое напряжение прибор True RMS (истинные среднеквадратические значения). True RMS прибор, на практике, использует несколько иной метод работы, в котором необходим только один умножитель. Аналоговые умножители должны иметь очень низкий температурный дрейф и смещение, что делает эти инструменты достаточно дорогими.
Аналоговая схема получения RMS-значений
Кроме того, можно сделать расчет RMS программным путем с последовательных цифровых значений измеряемых напряжений. Этот подход обычно используется в мультиметрах и цифровых осциллографах.
Соотношения фазного и линейного напряжения
Соотношение между напряжением линейным и фазным составляет 1,73. То есть при ста процентах мощности ЛН, напряжение фазы будет 58%. То есть, ЛН превышает ФН в 1,73 раза и при этом стабильно.
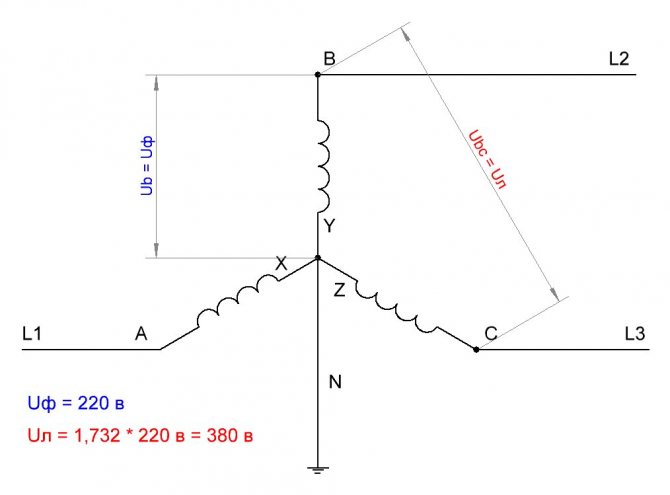
ФН и ЛН, отличие и соотношение
Напряжение в трёхфазной цепи оценивается по параметрам линейной составляющей. Обычно оно 380 вольт и тождественно 220 вольтам фазной компоненты сети трёхфазного электротока. В электрических сетях, где имеется четыре провода, напряжение 3-фазного тока обозначается 380/220В. Это позволяет подключить к подобной сети оборудование с 1-фазным потреблением электричества 220В и мощных приборов, которые могут работать от 380В.
Универсальной и приемлемой в большинстве случаев является трёхфазная цепь 380/220В 0-вым проводом. Электроприборы, которые функционируют от однофазного напряженья 220В, могут при подсоединении к паре проводов ФН питаться от ЛН.
Электрооборудование, которое запитывается от трёхфазной сети может работать, только если имеется подсоединение одновременно к 3-м выводам различных фаз. Тогда заземление не обязательно, но если изоляционный материал провода будет повреждён, то отсутствие 0-ого значительно увеличивает опасность удара электрическим током.
Важно! При понижении ЛН меняются величины ФН. При уже выясненном значении междуфазного напряжения определить величину ФН труда не составит
§47. Основные параметры переменного тока
При подключении к источнику переменного тока с синусоидально изменяющейся э. д. с. электрических цепей с линейными сопротивлениями в них будут действовать синусоидально изменяющиеся напряжения и проходить синусоидально изменяющиеся токи. Переменные токи, э. д. с. и напряжения характеризуются четырьмя основными параметрами: периодом, частотой, амплитудой и действующим значением.
Период.
Промежуток времени Т, в течение которого э. д. с, напряжение и или ток i (рис. 169, а) совершают полный цикл изменений, называется периодом. Чем быстрее вращается виток или ротор генератора переменного тока, тем меньше период изменения э. д. с. или тока.
Частота.
Число полных периодов изменения э. д. с, напряжения или тока в 1 с называется частотой,
f = 1 / T
Она измеряется в герцах (Гц), т. е. числом периодов в секунду. Чем больше частота, тем меньше период изменения тока, напряжения или э. д. с. (рис. 169,б). В Советском Союзе все электрические станции переменного тока вырабатывают ток, изменяющийся с частотой 50 Гц, т. е. 50 периодов в секунду. В автоматике и радиотехнике применяют электрические токи и более высоких частот. Такие частоты измеряются в килогерцах (1 кГц=10 3 Гц) и мегагерцах (1 МГц=10 6 Гц).
Рис. 169. Кривые изменения синусоидального переменного тока при различной частоте
Из рис. 169,а следует, что в течение времени одного периода Т фаза ωt тока (э. д. с. или напряжения) изменяется на угол 360°, или 2π радиан. Поэтому
ω = 2π/T = 2πf
Эту величину называют угловой частотой переменного тока, она имеет размерность рад/с.
Амплитуда.
Наибольшее значение переменного тока (переменных э. д. с. и напряжения) называют амплитудным значением, или амплитудой. В рассмотренном нами простейшем генераторе переменного тока (см. рис. 168, а) э. д. с. е дважды достигает амплитудного значения: во время первого полуоборота +Ет (направлена от начала витка к его концу), а во время второго полуоборота — Ет (направлена от конца витка к его началу).
Точно так же за один период ток i 2 раза достигает амплитудного значения: Iт и — Iт. Амплитудное значение тока, напряжения и э. д. с. в формулах обозначают соответствующими буквами с индексами «т», т. е. Iт Uт, Ет и др.
Действующее значение.
Ток, напряжение и э. д. с, действующие в электрической цепи в каждый отдельный момент времени, определяются так называемыми мгновенными значениями. Эти значения принято обозначать строчными буквами i, и, е. Однако судить о переменных э. д. с, токе или напряжении по их мгновенным значениям неудобно, так как эти значения непрерывно меняются.
Поэтому оценивать способность переменного тока совершать механическую работу или создавать тепло принято по действующему его значению. Под действующим значением переменного тока понимают силу такого постоянного тока (прямая 2 на рис. 169,а), который, проходя по проводнику в течение некоторого времени (например, в течение одного периода или 1 с), выделит в нем такое же количество тепла (произведет такую же механическую работу), как и данный переменный ток (кривая 1).
Действующие значения тока, напряжения и э. д. с. обозначают соответственно I, U, Е.
При синусоидальном переменном токе:
I = Iт / √2 = 0,707 Iт
Если известно действующее значение тока I, то его амплитудное значение:
Iт = √2 I = 1,41 I
Аналогично для синусоидальных напряжений и э. д. с.:
U / Uт = Е1 / Ет = 1 / √2 = 0,707
На практике для характеристики параметров переменного тока используют, главным образом, действующие значения тока, напряжения и э. д. с. Например, когда говорят, что напряжение в осветительной сети переменного тока составляет 220 В или что по цепи проходит ток 100 А, то это значит, что в данной сети действующее значение напряжения равно 220 В или что действующее значение тока, проходящего по данной цепи, равно 100 А.
Электрическая энергия и механическая работа, создаваемые переменным током в различных электрических устройствах, пропорциональны действующим значениям тока и напряжения. Большая часть существующих приборов для измерения переменного тока измеряет действующие значения тока, напряжения и э. д. с.
Источник
Дисперсия, ее виды, среднеквадратическое отклонение.
Дисперсия случайной величины — мера разброса данной случайной величины, т. е. её отклонения отматематического ожидания. В статистике часто употребляется обозначение или . Квадратный корень из дисперсии называется среднеквадратичным отклонением, стандартным отклонением или стандартным разбросом.
Общая дисперсия (σ 2 ) измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Вместе с тем, благодаря методу группировок можно выделить и измерить вариацию, обусловленную группировочным признаком, и вариацию, возникающую под влиянием неучтенных факторов.
Межгрупповая дисперсия (σ 2 м.гр) характеризует систематическую вариацию, т. е. различия в величине изучаемого признака, возникающие под влиянием признака – фактора, положенного в основание группировки.
Среднеквадратическое отклонение (синонимы: среднее квадратическое отклонение, среднеквадратичное отклонение, квадратичное отклонение; близкие термины: стандартное отклонение, стандартный разброс) — в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величиныотносительно её математического ожидания. При ограниченных массивах выборок значений вместо математического ожидания используется среднее арифметическоесовокупности выборок.
Среднеквадратическое отклонение измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами. Определяется какквадратный корень из дисперсии случайной величины.
Среднеквадратическое отклонение:
Стандартное отклонение (оценка среднеквадратического отклонения случайной величины x относительно её математического ожидания на основе несмещённой оценки её дисперсии):
где — дисперсия; — i-й элемент выборки; — объём выборки; — среднее арифметическое выборки:
Следует отметить, что обе оценки являются смещёнными. В общем случае несмещённую оценку построить невозможно. Однако оценка на основе оценки несмещённой дисперсии является состоятельной.
Действующее и среднее значения переменного тока
Действующее значение переменного тока численно равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, выделяет за время, равное 1 периоду, одинаковое количество тепла. Все приборы показывают действующее значение
Если левые части уравнения равны, то и правые будут тоже равны. Приравняв правые части и выполнив операцию интегрирования, получим:
Среднее арифметическое значение переменного тока определяется в течении полупериода; если через поперечное сечение проводника в течении 1 полупериода будет протекать один и тот же заряд при постоянном и переменном токе, то такое значение постоянного тока будет равно среднему значению переменного тока
Среднее значение тока за период равно нулю.
Коэффициенты формы и амплитуды
Отношение действующего значения переменного тока (напряжения или ЭДС) к среднему значению называется коэффициентом формы
, а отношение амплитудного значения к действующему –коэффициентом амплитуды .
Для синусоидального тока:
, а .
Для кривых, имеющих более острую форму, чем синусоида:
;.
Начальная фаза. Сдвиг фаз
| Предположим, что в магнитном поле генератора находится два одинаковых витка, сдвинутых в пространстве друг относительно друга на угол
. При вращении в них буду находится ЭДС одинаковой частоты и амплитуды. |
Но т.к. витки сдвинуты в пространстве, то наводимая в них ЭДС будет достигать амплитудных и нулевых значений не одновременно.
В начальный момент времени
ЭДС витка будет:
В этих выражениях углы
иназываютсяфазными , илифазой . Углыиназываютсяначальной фазой . Фазный угол определяет значение ЭДС в любой момент времени, а начальная фаза определяет значение ЭДС в начальный момент времени.
Разность начальных фаз двух синусоидальных величин одинаковой частоты и амплитуды называется углом сдвига фаз
Разделив угол сдвига фаз на угловую частоту, получим время, прошедшее с начала периода:
| Если угол сдвига фаз составляет 1800, то такие ЭДС находятся в противофазе |
Графическое изображение синусоидальных величин
Синусоидальные величины можно изображать графически при помощи синусоид или вращающихся векторов.
Любая синусоидальная величина характеризуется:
- амплитудой;
- угловой частотой;
- начальной фазой.
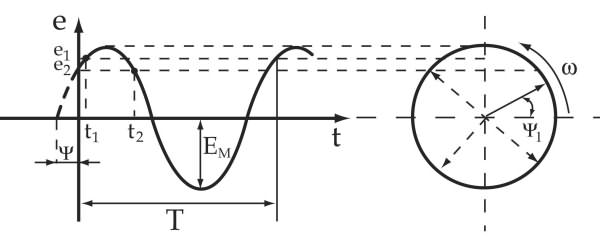
При изображении величины с помощью синусоиды ординаты синусоиды в масштабе представляют собой мгновенное значение, абсциссы – промежутки времени.
При этом длина вектора равна амплитудному значению величины, угол
между положительным направлением оси абсцисс и векторов даст начальную фазу. Вектор вращается против часовой стрелки с угловой скоростью. Проекция конца вектора на ось ординат даст мгновенное значение синусоидальной величины.
Совокупность нескольких синусоид называется синусоидальной (волновой) диаграммой.
Совокупность нескольких векторов называется векторной диаграммой.
Сложение и вычитание синусоидальных величин
. Для сложения двух синусоидальных величин с помощью синусоид необходимо сложить их ординаты в каждый момент времени.
Для того, чтобы сложить две величины с помощью векторов, необходимо к концу первого вектора добавить второй, не изменяя его величины и направления. Соединив начало первого вектора с концом второго, получим суммарный вектор.
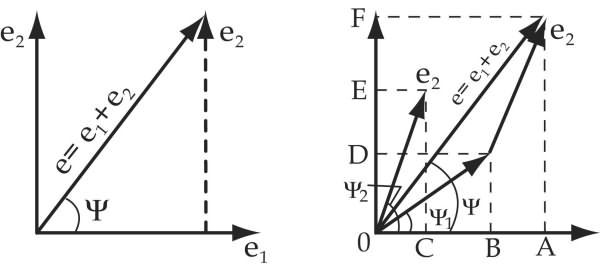
StudFiles.ru
Информация о напряжении
Напряжение — работа электрического тока, при которой происходит перемещение заряда из одной точки в другую. Оно имеет векторное направление. Электрическим током является движение заряженных элементарных частиц под воздействие электромагнитного поля.
Некоторые начинающие физики не знают, в чем измеряется напряжение
Знать это очень важно, поскольку элементы электрической цепи можно рассчитать неверно. Единицей измерения тока является ампер (А), а напряжения — вольт (В). В последнем случае применяется вольтметр — прибор, измеряющий величину напряжения или разности потенциалов
Он подключается параллельно в систему. Например, нужно измерить его значение на лампочке накаливания. Для этого необходимо подключиться параллельно к ней, а не последовательно
В последнем случае применяется вольтметр — прибор, измеряющий величину напряжения или разности потенциалов. Он подключается параллельно в систему. Например, нужно измерить его значение на лампочке накаливания. Для этого необходимо подключиться параллельно к ней, а не последовательно.
Физический смысл
Под физическим смыслом напряжения или разности потенциалов понимают работу, необходимую для перемещения точечного заряда в 1 Кл из одного места в другое. В этом случае переносится только положительный потенциал. При этом возникает электродвижущая сила (ЭДС), которая называется напряжением или разностью потенциалов.
Для понимания физического смысла следует рассмотреть более простой пример. Пусть существует некоторая система, состоящая из насоса, труб и крана. Насос — напряженность электрического поля, трубы — провода, а кран — сопротивление системы. При включении первого происходит закачивание воды. Если немного приоткрыть кран, то она польется маленькой струйкой. При открытии его полностью жидкость будет уходить более интенсивно.
Формулы для вычислений
Все формулы для расчетов построены на законах Ома. Их всего два: для участка и для всей цепи. Формулировка первого: ток, протекающий на искомом участке, прямо пропорционален U и обратно пропорционален R. Его математическая запись имеет такой вид: I=U/R. Из последнего получаются такие соотношения:
- U=IR.
- R=U/I.
- P=IU=(I2 )R=(U2 )/R, где Р — мощность.
Для полной цепи закон формулируется иначе: ток I прямо пропорционален ЭДС (E) и обратно пропорционален алгебраической сумме внешнего R и внутреннего r сопротивлений. Следует отметить, что r — проводимость источника питания. Записывается он в таком виде: I=E/(R+r). Физики вывели следующие соотношения, помогающие при расчетах:
- Е=I (R+r).
- R=(E/I)-r.
- r=(E/I)-R.
- Р=ЕI=(E2 )/(R+r)=(R+r)I2.
Тождества для переменного тока
Напряжение при переменном токе классифицируется на определенные виды. К ним относятся следующие:
- Мгновенное или действующее — параметр, который измеряют приборы (Um).
- Амплитудное — величина, характеризующее максимальную величину в определенный момент времени. Расчитывается по формуле с учетом угловой частоты (w), времени (t) и угла между фазами (f), который измеряется осциллографом: u (t)=Uмsin (wt+f).
- Среднеквадратичное (Uq) — величина, вычисляемая по формуле: Uq=0,7073Uм).
Для расчета следует иметь знания об индуктивной Xl, емкостной Xc и резистивной R нагрузках. Первая — проводимость всех элементов, содержащих индуктивность (катушки, трансформаторы, электродвигатели). Во втором случае учитываются все емкостные радиодетали (варисторы и конденсаторы). Резистивная нагрузка включает все значения резисторов.
Полный импеданс цепи (Z) равен сумме всех элементов, содержащий активную, индуктивную и емкостную. Специалисты рекомендуют использовать такие формулы, необходимые для расчетов:
- Xl=wL.
- Хс=1/wC.
- Z=R+Xc+Xl.
- I=Uм/Z.
- Uм=IZ.
- Z=Uм/I.
Четвертая формула является законом Ома для участка цепи, которую следует применять при переменных токах.
Таким образом, при помощи формулы напряжения можно рассчитывать не только основные параметры электричества для постоянного и переменного токов, но и его допустимые величины для человека.
https://youtube.com/watch?v=jygkQ7RLq5A
Краткая история электричества
Кто изобрел электричество? А никто! Люди постепенно понимали, что это такое и как им пользоваться.
Все началось в 7 веке до нашей эры, в один солнечный (а может и дождливый, кто знает) день. Тогда греческий философ Фалес заметил, что, если потереть янтарь о шерсть, он будет притягивать легкие предметы.
Потом были Александр Македонский, войны, христианство, падение Римской империи, войны, падение Византии, войны, средневековье, крестовые походы, эпидемии, инквизиция и снова войны. Как вы поняли, людям было не до какого-то там электричества и натертых шерстью эбонитовых палочек.
В каком году изобрели слово «электричество»? 1600 году английский естествоиспытатель Уильям Гилберт решил написать труд «О магните, магнитных телах и о большом магните — Земле». Именно тогда и появился термин «электричество».
Через сто пятьдесят лет, в 1747 году Бенджамин Франклин, которого мы все очень любим, создал первую теорию электричества. Он рассматривал это явление как флюид или нематериальную жидкость.
Именно Франклин ввел понятие положительного и отрицательного зарядов (до этого разделяли стеклянное и смоляное электричество), изобрел молниеотвод и доказал, что молния имеет электрическую природу.
Бенджамина любят все, ведь его портрет есть на каждой стодолларовой купюре. Помимо работы в точных науках, он был видным политическим деятелем. Но вопреки распространенному заблуждению, Франклин не был президентом США.
Дальше пойдет перечисление важных для истории электричества открытий.
1785 год – Кулон выясняет, с какой силой противоположные заряды притягиваются, а одноименные отталкиваются.
1791 год – Луиджи Гальвани случайно заметил, что лапки мертвой лягушки сокращаются под действием электричества.
Принцип работы батарейки основан на гальванических элементах. Но кто создал первый гальванический элемент? Основываясь на открытии Гальвани, другой итальянский физик Алессандро Вольта в 1800 году создает столб Вольта – прототип современной батарейки.
На раскопках рядом с Багдадом нашли батарейку возрастом больше двух тысяч лет. Какой древний айфон с ее помощью подзаряжали – остается загадкой. Зато известно точно, что батарейка уже «села». Этот случай как бы говорит: может быть, люди знали об электричестве намного раньше, но потом что-то пошло не так.
Уже в 19 веке Эрстед, Ампер, Ом, Томсон и Максвелл совершили настоящую революцию. Был открыт электромагнетизм, ЭДС индукции, электрические и магнитные явления связали в единую систему и описали фундаментальными уравнениями.
Кстати! Если у вас нет времени, чтобы самостоятельно разбираться со всем этим, для наших читателей сейчас действует скидка 10% на любой вид работы
20 век принес квантовую электродинамику и теорию слабых взаимодействий, а также электромобили и повсеместные линии электропередач. Кстати, знаменитый электромобиль Тесла работает на постоянном токе.
Конечно, это очень краткая история электричества, и мы не упомянули очень много имен, которые повлияли на прогресс в этой области. Иначе пришлось бы написать целый многотомный справочник.
Расчет линейного и фазного напряжения
Сети с линейным током нашли широкое применение за счет своих характеристик меньшей травмоопасности и легкости разведения такой электропроводки. Все электрические устройства в этом случае соединены только с одним фазным проводом, по которому и идет ток, и только он один и представляет опасность, а второй – это земля.
Рассчитать такую систему несложно, можно руководствоваться обычными формулами из школьного курса физики. Кроме того, для измерения этого параметра сети, достаточно использовать обычный мультиметр, в то время как для снятия показаний подключения фазного типа, придется задействовать целую систему оборудования.
Для подсчета напряжения линейного тока, применяют формулу Кирхгофа:
∑ Ik = 0;
Уравнение которой гласит, что каждой из частей электрической цепи, сила тока равна нулю – k=1.
И закон Ома:
I=U/R;
Используя их, можно без труда произвести расчеты каждой характеристики конкретного клейма или электросети.
В случае разделения системы на несколько линий, может появиться необходимость рассчитать напряжение между фазой и нулем:
IL = IF;
Эти значения являются переменными, и меняются при разных вариантах подключения. Поэтому, линейные характеристики идентичны фазовым.
Однако, в некоторых случаях, требуется вычислить чему равно соотношение фазы и линейного проводника.
Для этого, применяют формулу:
Uл=Uф∙√3, где:
Uл – линейное, Uф – фазовое. Формула справедлива, только если – IL = IF.
При добавлении в электросистему дополнительных отводящих элементов, необходимо и персонально для них рассчитывать фазовое напряжение. В этом случае, значение Uф заменяется на цифровые данные самостоятельного клейма.
При подключении промышленных систем к электросети, может появиться необходимость в расчете значения реактивной трехфазной мощности, которое вычисляется по следующей формуле:
Q = Qа + Qb + Qс;
Идентичная структура формулы активной мощности:
P = Pа + Pb + Pс;
Примеры расчета:
Например, катушки трехфазного источника тока подключены по схеме «звезда», их электродвижущая сила 220В. Необходимо вычислить линейное напряжение в схеме.
Линейные напряжения в этом подключении будут одинаковы и определяются как:
U1=U2=U3= √3 Uф=√3*220=380 В.