Что такое активное сопротивление

Векторная диаграмма и полное сопротивление цели

Мгновенную величину общего напряжения можно представить суммой мгновенных напряжений на отдельных элементах схемы:

u = u1R + uL + uC + u2R,

Имея в виду несовпадение по фазе активных и реактивных напряжений, общее напряжение получим векторным сложением:

U = U2R + UL + UC +U2R

Для построения векторной диаграммы находим:

U1R = IR1; U2R = IR2; UL = IXL; UC = IXC.

В зависимости от соотношения величин реактивных сопротивлений индуктивности и емкости можно отметить три случая:

1. ХL>ХC . Для этого случая векторная диаграмма представлена на рис. 14.2. На диаграмме построены треугольники напряжений для катушки и конденсатора и найдены векторы напряжения U1 и U2 на этих элементах.

Векторная сумма напряжений U1 + U2 = U дает общее напряжение в цепи. Вместе с тем вектор U является гипотенузой прямоугольного треугольника напряжений, катеты которого — активное и реактивное напряжения цепи (Uа и Uр). Так как векторы активных составляющих напряжения направлены в одну сторону, их численные значения складываются: Ua = U1R + U2R.

Векторы реактивных составляющих напряжения направлены по одной прямой в противоположные стороны, поэтому им придают разные знаки: реактивное напряжение индуктивности считают положительным, а напряжение емкости — отрицательным: Uр = UL — UC .

При одинаковом токе во всех элементах цепи UL>UC . Ток отстает от общего напряжения по фазе на угол φ. Из треугольника напряжений следует

где R = R1 + R2 и X = XL — XC общее и активное и реактивное сопротивление цепи. Полное сопротивление цепи — Z.

Эти сопротивления графически можно изобразить сторонами прямоугольного треугольника сопротивлений, который получают уже известным способом из треугольника напряжений.

Полное сопротивление цепи Z является коэффициентом пропорциональности между действующими величинами тока и общего напряжения цепи:

U = IZ; I = U/Z; Z = U/I.

Из треугольников напряжения и сопротивлений определяют следующие величины:

Угол сдвига по фазе между напряжением и током в цепи положительный (φ>0) (фазовые токи отсчитываются от вектора тока).

2. ХLCВекторная диаграмма изображена на рис. 14.3, где ULC , поэтому общее напряжение отстает от тока на угол φ

Реактивное сопротивление цепи носит емкостный характер.

Расчетные формулы для первого случая остаются без изменения и для второго случая.

3. XL = ХC . В этом случае реактивные составляющие напряжения катушки и конденсатора равны по величине и взаимно компенсированы: UL = UC (рис. 14.4). Поэтому реактивная составляющая общего напряжения и общее реактивное сопротивление равны нулю, а полное сопротивление цепи Z = R.

Общее напряжение совпадает по фазе с током и равно по величине активной

составляющей напряжения.

Угол φ сдвига фаз между током и общим напряжением равен нулю.

Ток в цепи и общее напряжение связаны формулой

U = IR, или I = U/R.

В случае XL = ХC в цепи имеет место явление резонанса напряжений.

СДЕЛАЕМ УПРОЩЕННЫЙ РАСЧЕТ ТРАНСФОРМАТОРА 220/36 ВОЛЬТ.

Мощность во вторичной цепи: Р_2 = U_2 · I_2 = 60
ватт

Где:Р_2
– мощность на выходе трансформатора, нами задана 60 ватт
;

U
_2
– напряжение на выходе трансформатора, нами задано 36 вольт
;

I
_2
– ток во вторичной цепи, в нагрузке.

КПД трансформатора мощностью до 100 ватт
обычно равно не более η = 0,8
.КПД определяет, какая часть мощности потребляемой от сети идет в нагрузку. Оставшаяся часть идет на нагрев проводов и сердечника. Эта мощность безвозвратно теряется.

Определим мощность потребляемую трансформатором от сети с учетом потерь:

Р_1 = Р_2 / η = 60 / 0,8 = 75 ватт
.

Мощность передается из первичной обмотки во вторичную через магнитный поток в магнитопроводе.Поэтому от значения Р_1

, мощности потребляемой от сети 220
вольт,
зависит площадь поперечного сечения магнитопровода S
.

Магнитопровод – это сердечник Ш – образной или О – образной формы, набранный из листов трансформаторной стали. На сердечнике будут располагаться первичная и вторичная обмотки провода.

Площадь поперечного сечения магнитопровода рассчитывается по формуле:

S = 1,2 · √P_1.

Где:S
– площадь в квадратных сантиметрах,P
_1 – мощность первичной сети в ваттах.

S = 1,2 · √75 = 1,2 · 8,66 = 10,4 см².

По значению S
определяется число витков w
на один вольт по формуле:

w = 50/S

В нашем случае площадь сечения сердечника равна S = 10,4 см.кв.

w = 50/10,4 = 4,8
витка на 1 вольт.

Рассчитаем число витков в первичной и вторичной обмотках.

Число витков в первичной обмотке на 220 вольт:

W1 = U_1 · w = 220 · 4.8 = 1056 витка.

Число витков во вторичной обмотке на 36 вольт:

W2 = U_2 · w = 36 · 4,8 = 172.8 витков
,

округляем до 173 витка
.

В режиме нагрузки может быть заметная потеря части напряжения на активном сопротивлении провода вторичной обмотки. Поэтому для них рекомендуется число витков брать на 5-10 % больше рассчитанного. Возьмем W2 = 180 витков.

Величина тока в первичной обмотке трансформатора:

I_1 = P_1/U_1 = 75/220 = 0,34 ампера
.

Ток во вторичной обмотке трансформатора:

I_2 = P_2/U_2 = 60/36 = 1,67 ампера.

Диаметры проводов первичной и вторичной обмоток определяются по значениям токов в них исходя из допустимой плотности тока, количества ампер на 1 квадратный миллиметр площади проводника. Для трансформаторов плотность тока,для медного провода,

принимается 2 А/мм² .

При такой плотности тока диаметр провода без изоляции в миллиметрах определяется по формуле: d = 0,8√I
.

Для первичной обмотки диаметр провода будет:

d_1 = 0,8 · √1_1 = 0,8 · √0,34 = 0,8 · 0,58 = 0,46 мм. Возьмем 0,5 мм
.

Диаметр провода для вторичной обмотки:

d_2 = 0,8 · √1_2 = 0,8 · √1,67 = 0,8 · 1,3 = 1,04 мм. Возьмем 1,1 мм.

ЕСЛИ НЕТ ПРОВОДА НУЖНОГО ДИАМЕТРА,
то можно взять несколько, соединенных параллельно, более тонких проводов. Их суммарная площадь сечения должна быть не менее той, которая соответствует рассчитанному одному проводу.

Площадь поперечного сечения провода определяется по формуле:

s = 0,8 · d².

где
: d – диаметр провода
.

Например: мы не смогли найти провод для вторичной обмотки диаметром 1,1
мм.

Площадь поперечного сечения провода диаметром 1,1
мм. равна:

s = 0,8 · d² = 0,8 · 1,1² = 0,8 · 1,21 = 0,97 мм²
.

Округлим до 1,0
мм².

Изтаблицывыбираем диаметры двух проводов сумма площадей сечения которых равна 1.0 мм².

Например, это два провода диаметром по 0,8 мм
. и площадью по0,5 мм²
.

Или два провода: – первый диаметром 1,0 мм
. и площадью сечения 0,79 мм²
,– второй диаметром 0,5 мм
. и площадью сечения 0,196 мм²
.что в сумме дает: 0,79 + 0,196 = 0,986 мм².

Намотка катушки ведется двумя проводами одновременно, строго выдерживается равное количество витков обоих проводов. Начала этих проводов соединяются между собой. Концы этих проводов также соединяются.

Получается как бы один провод с суммарным поперечным сечением двух проводов.

Смотрите статьи:– «Как намотать трансформатор на Ш-образном сердечнике».– «Как изготовить каркас для Ш – образного сердечника».

Электрический аппарат – трансформатор используется для преобразования поступающего переменного напряжения в другое – исходящее, к примеру: 220 В в 12 В (конкретно это преобразование достигается использованием понижающего трансформатора). Прежде чем разбираться с тем, как рассчитать трансформатор, вы в первую очередь должны обладать знаниями о его структуре.

Простейший трансформатор является компоновкой магнитопровода и обмоток 2-х видов: первичной и вторичной, специально намотанных на него. Первичная обмотка воспринимает подающееся переменное напряжение от сети (н-р: 220 В), а вторичная обмотка, посредством индуктивной связи создает другое переменное напряжение. Разность витков в обмотках влияет на выходное напряжение.

Расчет индуктивности некоторых типов высокочастотных катушек

Приведем расчетные формулы для наиболее часто используемых конструкций.

Индуктивность прямолинейного провода с круглым сечением. Сюда относятся индуктивные элементы ДЦВ диапазона, оценка индуктивности проволочных выводов резисторов, конденсаторов, активных элементов:

L_пр = 0,002l(ln [4l/d]-1,75);
lL_прl = мкГн,

где = см — длина провода; d = см — диаметр провода без изоляции.

Индуктивность круглого витка из провода круглого сечения. Используют для оценки индуктивности рамочных (резонансных) антенн, катушек связи и т.п.:

L_кр = 0,00628В (ln [8D/d]-1,75),

где = см — диаметр витка.

Индуктивность замкнутого геометрического контура всегда будет меньше индуктивности прямого провода той же длины. Наибольшей индуктивностью обладает тот из замкнутых геометрических контуров одинакового периметра, который имеет наибольшую площадь. Следовательно, наибольшая индуктивность будет у контура, имеющего форму окружности.

Индуктивность однослойной цилиндрической катушки (рис. 4.2).

Рис. 4.2. Элементы однослойной цилиндрической катушки

Если длина намотки l = т • N (N — число витков) соответствует неравенству
l >> D, то приемлема формула

L = π2 · D2 N2
10-3 / l мкГн.

Если длина намотки катушки соизмерима с ее диаметром, то вводится поправочный коэффициент
L. Значение этого коэффициента находят по графику, изображенному на рис. 4.3, а величину индуктивности определяют из выражения

L = L • N2 • D • 10-3мкГн,

Рис. 4.3. Графическая зависимость поправочного коэффициента

Индуктивность многослойной цилиндрической катушки. Для получения больших значений индуктивности используют многослойные катушки. Индуктивность таких катушек можно определить по предыдущей формуле, но поправочный коэффициент
L (рис. 4.4) будет зависеть от соотношения толщины намотки к наружному диаметру
t/D.

Рис. 4.4. Поправочный коэффициент для многослойной катушки

Индуктивность катушки с сердечником. Получить оптимальное значение индуктивности и добротности, обеспечить точную установку индуктивности позволяет применение сердечников.
Индуктивность катушки с сердечником
L_С =
μ_СL, где
L — индуктивность той же катушки без сердечника;
μ_С — действующая магнитная проницаемость. Если
μ — магнитная проницаемость материала, из которого выполнен сердечник, то отношение
К_μ =
μ_с/μ — коэффициент использования магнитных свойств. Он зависит от конструкции катушки и определяется экспериментально.

Для ферромагнетиков (ферриты, карбонильное железо)
μ_с > 1, для диамагнетиков (латунь, медь, алюминий)
μ_с < 1. Таким образом, используя ферромагнетики, повышают индуктивность катушки, а используя диамагнетики, понижают ее.

Индуктивность тороидальной катушки (с кольцевым сердечником) определяют по формуле

L_тор = 0,00628 • μ
• N2(D — √D2_T
— D_в),

где D_Т — диаметр осевой линии
тора, см; D_В — средний диаметр витка;
μ — начальная магнитная проницаемость материала тора.

Индуктивность экранированной катушки.
Экранирование выполняют или шунтированием магнитного поля ферромагнитным экраном с большой относительной магнитной проницаемостью или вытеснением магнитного поля экраном из диамагнетика (медь, латунь, алюминий). Для экранирования ВЧ катушек используют, как правило, второй способ.

Индуктивность цилиндрической катушки с алюминиевым цилиндрическим экраном

L = L • [1-(D/D_э)3]• [1-(I/2I_э)2],

где L — индуктивность катушки без экрана; D — диаметр обмотки;
D_Э -диаметр экрана;
l — длина намотки; l_Э — длина экрана. Добротность экранированной катушки всегда ниже, а собственная емкость выше катушки без экрана.

Катушка индуктивности в цепи переменного тока

В цепи переменного тока в катушке индуктивности происходит следующий процесс:

1. ток возбуждает в катушке электромагнитное поле. Поскольку он переменный, то и параметры электромагнитного поля во времени меняются, то есть оно тоже переменное;
2. переменное магнитное поле в соответствии с законом электромагнитной индукции возбуждает в самой катушке ЭДС. Ее так и называют — ЭДС самоиндукции. Она всегда идет против направления изменения силы тока. Следовательно, в первой половине полупериода, когда сила тока возрастает, катушка это нарастание сдерживает. При этом часть энергии электричества накапливается в формируемом катушкой магнитном поле;
3. во второй половине полупериода, катушка, наоборот, противостоит снижению силы тока, возвращая в цепь накопленную в виде магнитного поля энергию.

Таким образом, катушка индукции оказывает сопротивление источнику переменного тока. Это сопротивление имеет иную природу, нежели активное, преобразующее электрическую энергию в тепло.

Сопротивление катушки энергию не потребляет, а лишь аккумулирует ее и затем снова возвращает в цепь, меняя характер протекания в ней тока. Его называют индуктивным. В противоположность активному, оно, как и емкостное сопротивление конденсатора, является реактивным.

Эффект проявляется тем сильнее, чем выше частота переменного тока, то подтверждается формулой расчета индуктивного сопротивления: XL = w*L = 2 π * f * L, где:

• XL — индуктивное сопротивление, Ом;
• W — круговая частота переменного тока, рад/с;
• F — частота переменного тока, Гц;
• L — индуктивность катушки, Гн.

Индуктивное сопротивление, несмотря на иной принцип действия, измеряется в тех же единицах, что и активное — Омах. Таким образом, в цепях переменного тока катушка индуктивности выступает ограничителем силы тока и нагрузку, в отличие от цепи постоянного, вводить не требуется.

Зависимость индуктивного сопротивления катушки от частоты тока позволяет использовать данный элемент помимо прочего, для фильтрации высокочастотных помех или сигналов. Например, при установке его в схеме динамика, последний воспроизводит только низкие частоты, то есть играет роль сабвуфера.

На преодоление индуктивного сопротивления источник расходует часть мощности — это реактивная мощность (Wр). Остальное называют активной или полезной мощностью (Wа) — она производит полезную работу. Вместе реактивная и активная мощности образуют полную: Wр + Wа = Wпол.

График происходящих процессов в катушке индуктивности

Доля активной мощности характеризуется параметром cosϕ: cosϕ = Wа / W пол. Полную мощность принято измерять в вольт-амперах (ВА). Именно эти единицы указываются в характеристике источников бесперебойного питания (ИБП) и дизельных электрогенераторов. Активная мощность измеряется в привычных ваттах (Вт).

Все сказанное имеет отношение к потребителям с электродвигателями и трансформаторами, поскольку обмотки этих элементов по сути, являются катушками индуктивности. То есть если на шильдике импульсного блока питания компьютера указано, что его мощность составляет 400 Вт и cosϕ = 0,7, то от «бесперебойника» данное устройство потянет мощность Wпол = Wа / cosϕ = 400 0,7 = 571,4 ВА.

При большом количестве подобных потребителей, затраты на реактивную мощность существенно перегружают генераторы электростанций, ввиду чего в энергосетях применяют установки компенсации реактивной мощности (УКРМ).

При включении катушки индуктивности в цепь постоянного тока процесс, описанный в пунктах 1-3, также имеет место, только не все время, а в момент включения/отключения.

Если собрать простейшую цепь из последовательно установленных выключателя, катушки и лампы, можно видеть, что лампочка загорается при замыкании цепи с запаздыванием и также с запаздыванием гаснет после размыкания.

Объясняется это тем, что ток в момент включения меняется от нулевого значения до максимума, также в момент отключения его значение меняется, хоть и очень быстро, от максимума до нуля. В первом случае катушка накапливает в себе часть энергии в виде магнитного поля, во втором — отдает ее лампе, отчего та и горит после размыкания цепи.

Способы расчёта

Существует несколько основных способов определить индуктивность катушки. Все формулы, которые будут использоваться в расчётах, легко можно найти в справочной литературе или интернете. Весь процесс вычисления довольно простой и не составит труда для людей, имеющих элементарные математические и физические знания.

Через силу тока

Этот расчёт считается самым простым способом определения индуктивности катушки. Формула через силу тока вытекает из самого термина. Какова индуктивность катушки — можно определить по формуле: L=Ф/I, где:

• L — индуктивность контура (в генри);
• Ф — величина магнитного потока, измеряемого в веберах;
• I — сила тока в катушке (в амперах).

https://youtube.com/watch?v=FCddea1HYm0

Соленоид конечной длины

Соленоид представляет собой тонкую длинную катушку, где толщина обмотки значительно меньше диаметра. В этом случае расчёты ведутся по той же формуле, что и через силу тока, только величина магнитного потока будет определяться следующим образом: Ф=µ0NS/l, где:

• µ0 — магнитная проницаемость среды, определяющаяся по справочным таблицам (для воздуха, который принимается по умолчанию в большинстве расчётов, она равна 0,00000126 генри/метр);
• N — количество витков в катушке;
• S — площадь поперечного сечения витка, измеряемая в квадратных метрах;
• l — длина соленоида в метрах.

Коэффициент самоиндукции соленоида можно рассчитать и исходя из способа определения энергии магнитного потока поля. Это более простой вариант, но он требует наличия некоторых величин. Формула для нахождения индуктивности — L=2W/I 2 , где:

• W — энергия магнитного потока, измеряемая в джоулях;
• I — сила тока в амперах.

https://youtube.com/watch?v=Y8-saxraVlk

Катушка с тороидальным сердечником

В большинстве случаев тороидальная катушка наматывается на сердечник, изготовленный из материала, обладающего большой магнитной проницаемостью. В этом случае для расчётов индуктивности можно использовать формулу для прямого соленоида бесконечной длины. Она имеет такой вид: L=N µ0 µS/2 πr, где:

• N — число витков катушки;
• µ — относительная магнитная проницаемость;
• µ0 — магнитная постоянная;
• S — площадь сечения сердечника;
• π — математическая постоянная, равная 3,14;
• r — средний радиус тора.

Длинный проводник

Большинство таких квазилинейных проводников имеет круглое сечение. В этом случае величина коэффициента самоиндукции будет определяться по стандартной формуле для приближённых расчётов: L= µ0l (µelnl/r+ µi/4)/2 π. Здесь используются следующие обозначения:

• l — длина проводника в метрах;
• r — радиус сечения провода, измеряемый в метрах;
• µ0 — магнитная постоянная;
• µi — относительная магнитная проницаемость, характерная для материала, из которого изготовлен проводник;
• µe — относительная магнитная проницаемость внешней среды (чаще всего принимается значение для вакуума, которое равняется 1);
• π — число Пи;
• ln — обозначение логарифма.

Автомобили

В автомобильной практике чаще используют словосочетание «дроссельный узел». При этом возможно использование одного из двух видов устройства, то есть механического или электрического дросселя. Он начинает работать после нажатия водителем педали газа, после чего дроссельная заслонка начинает свое движение. Вместе с этим регулируется подача топливно-воздушной смеси, которая поступает в двигательную систему. Эта заслонка соединяется со специальным датчиком, который передает информацию в компьютер, что позволяет определить необходимое количество топлива. В этом случае дроссель располагается между воздушным фильтром и двигателем автомобиля и крепится к двигательной системе.

ОБЩАЯ ЭЛЕКТРОТЕХНИКА И ЭЛЕКТРОНИКА. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ

Катушка индуктивности

— является пассивным компонентом электронных схем, основное предназначение которой является сохранение энергии в виде магнитного поля. Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.

Индуктивность (измеряется в Генри) — это эффект возникновения магнитного поля вокруг проводника с током. Ток, протекающий через катушку индуктивности, создает магнитное поле, которое имеет связь с электродвижущей силой (ЭДС) оказывающее противодействие приложенному напряжению.

Возникающая противодействующая сила (ЭДС) противостоит изменению переменного напряжения и силе тока в катушке индуктивности. Это свойство индуктивной катушки называется индуктивным сопротивлением. Следует отметить, что индуктивное сопротивление находится в противофазе к емкостному реактивному сопротивлению конденсатора в цепи переменного тока. Путем увеличения числа витков можно повысить индуктивность самой катушки.

§ 2.9. Закон Ома для электрической цепи переменного тока

Рассмотрим теперь более общий случай электрической цепи, в которой последовательно соединены проводник с активным сопротивлением R и малой индуктивностью, катушка с большой индуктивностью L и малым активным сопротивлением и конденсатор емкостью С (рис. 2.20).

Рис. 2.20

Чему равна амплитуда силы тока в такой цепи (колебательном контуре), если на ее концах поддерживается напряжение u(t) = U sin ωt?

Мы видели, что при включении по отдельности в цепь проводника с активным сопротивлением R, конденсатора емкостью С или катушки с индуктивностью L амплитуда силы тока определяется соответственно формулами (2.6.2), (2.7.3) и (2.8.4). Амплитуды же напряжений на резисторе, катушке индуктивности и конденсаторе связаны с амплитудой силы тока так:

В цепях постоянного тока напряжение на концах цепи равно сумме напряжений на отдельных последовательно соединенных участках цепи. Однако, если измерить результирующее напряжение на контуре и напряжения на отдельных элементах цепи переменного тока, окажется, что напряжение на контуре (действующее значение) не равно сумме напряжений на отдельных элементах.

Почему это так? Дело в том, что гармонические колебания напряжения на различных участках цепи сдвинуты по фазе друг относительно друга.

Действительно, квазистационарный ток в любой момент времени одинаков во всех участках цепи. Это значит, что одинаковы амплитуды и фазы токов, протекающих по участкам с емкостным, индуктивным и активным сопротивлением. Однако только на участке с активным сопротивлением колебания напряжения и силы тока совпадают по фазе. На конденсаторе колебания напряжения отстают по фазе от колебаний силы тока на π/2 (см. § 2.7), а на катушке индуктивности колебания напряжения опережают колебания силы тока на π/2 (см. § 2.8).

Векторная диаграмма электрической цепи

Для вывода закона Ома в случае электрической цепи переменного тока, изображенной на рисунке 2.20, нужно уметь складывать мгновенные колебания напряжений, сдвинутых по фазе друг относительно друга. Проще всего выполнять сложение нескольких гармонических колебаний с помощью векторных диаграмм, о которых было рассказано в § 1.11. Векторная диаграмма электрических колебаний в цепи позволит нам определить амплитуду силы тока в зависимости от амплитуды напряжения и сдвиг фаз между силой тока и напряжением.

Так как сила тока одинакова во всех участках цепи, то построение векторной диаграммы удобно начать с вектора силы тока _m. Этот вектор изобразим в виде вертикальной стрелки (рис. 2.21). Напряжение на резисторе совпадает по фазе с силой тока. Поэтому вектор _mR должен совпадать по направлению с вектором _m. Его модуль равен U_mR = I_mR.

Рис. 2.21

Колебания напряжения на катушке индуктивности опережают колебания силы тока на π/2 и соответствующий вектор и _mL должен быть повернут относительно вектора _m на π/2. Его модуль равен U_mL = IωL. Если считать, что положительному сдвигу фаз соответствует поворот вектора против часовой стрелки, то вектор _mL следует повернуть налево на π/2. (Можно было бы, конечно, поступить и наоборот.)

Вектор напряжения на конденсаторе _mC отстает по фазе от вектора _m на π/2 и поэтому повернут на этот угол относительно вектора _m направо. Его модуль равен .

Для нахождения вектора суммарного напряжения _m нужно сложить три вектора: _mR, _mL и _mC. Вначале удобнее сложить два вектора _mL и _mC (рис. 2.22).

Рис. 2.22

Модуль этой суммы равен , если . Именно такой случай изображен на рисунке. После этого, сложив вектор _mL + _mC с вектором _mR, получим вектор _m, характеризующий колебания напряжения в сети.

По теореме Пифагора (из треугольника АОВ):

или

Из равенства (2.9.2) можно найти амплитуду силы тока в цепи:

Это и есть закон Ома для электрической цепи переменного тока, изображенной на рисунке 2.20.

Благодаря сдвигу фаз между напряжениями на различных участках цепи полное сопротивление Z цепи (см. рис. 2.20) выражается так:

От амплитуд силы тока и напряжения можно перейти к действующим значениям этих величин. Они связаны друг с другом точно так же, как и амплитуды в формуле (2.9.3):

Мгновенное значение силы тока меняется со временем гармонически:

где φ_c, — разность фаз между силой тока и напряжением в сети. Она зависит от частоты со и параметров цепи R, L, С.

Сдвиг фаз между током и напряжением

Сдвиг фаз φ_c, между колебаниями силы тока и напряжения равен по модулю углу φ между векторами _m и _m (см. рис. 2.22). Как следует из этого рисунка,

Согласно рисунку 2.22, сила тока отстает от напряжения по фазе при условии . Поэтому сдвиг фаз φ_c = -φ и

В частных случаях цепей с активным, емкостным и индуктивным сопротивлениями из этой формулы получаются правильные значения сдвига фаз.

Свойства катушки индуктивности

Катушка индуктивности в электрической цепи хорошо проводит постоянный ток и в то же время оказывает сопротивление переменному току , поскольку при изменении тока в катушке возникает ЭДС самоиндукции , препятствующая этому изменению.

Катушка индуктивности обладает реактивным сопротивлением величина которого равна: , где- индуктивность катушки,-циклическая частота протекающего тока. Соответственно, чем больше частота тока, протекающего через катушку, тем больше её сопротивление.

При протекании тока катушка запасает энергию, равную работе, которую необходимо совершить для установления текущего тока . Величина этой энергии равна

При изменении тока в катушке возникает ЭДС самоиндукции, значение которой

Питание от сети переменного тока серии LR

До сих пор мы рассматривали чисто индуктивную катушку, но невозможно иметь чистую индуктивность, поскольку все катушки, реле или соленоиды будут иметь определенное сопротивление, независимо от того, насколько мало связано с витками используемого провода. Тогда мы можем рассматривать нашу простую катушку как последовательное сопротивление с индуктивностью (LR).

В цепи переменного тока, которая содержит как индуктивность L и сопротивление R, напряжение V будет векторная сумма двух компонентов напряжения, V _Rи V _L . Это означает, что ток, протекающий через катушку еще будет отставать от напряжения, но на величину меньше чем 90 ö в зависимости от значений V _Rи V _L .

Новый фазовый угол между напряжением и током известен как фазовый угол цепи и обозначается греческим символом фи, Φ .

Чтобы получить векторную диаграмму зависимости между напряжением и током, необходимо найти эталонный или общий компонент. В последовательно соединенной цепи RL ток является общим, так как один и тот же ток течет через каждый компонент. Вектор этой эталонной величины обычно рисуется горизонтально слева направо.

Из наших руководств о резисторах и конденсаторах, мы знаем, что ток и напряжение в цепи переменного резистивного тока, оба «в фазе» и, следовательно, вектор V _R рисуется с наложением на текущую или контрольную линию.

Из вышесказанного также известно, что ток «отстает» от напряжения в чисто индуктивной цепи и, следовательно, вектор V _L отображается на 90 o перед опорным током и в том же масштабе, что и V _R, это показано ниже.

Что зовется индуктивным сопротивлением

Когда на катушку подают переменное напряжение, ток, проходящий по ней, меняется согласно поданному напряжению. Это служит причиной изменения магнитного поля, создающего электродвижущую силу, препятствующую происходящему.

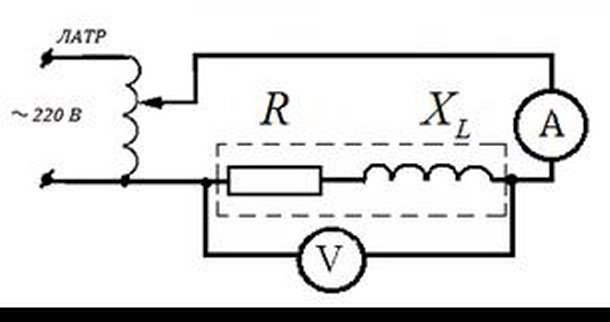
Схема для измерения

В такой цепи имеется зависимость электрических параметров от двух видов: обычного и индуктивного. Они обозначаются, соответственно, как R и XL.

На обычном происходит выделение мощности. Однако на реактивных элементах она является нулевой. Это связано с постоянным изменением направления переменного тока.

В течение одного периода колебаний энергия дважды закачивается в катушку и столько же раз возвращается в источник.

Определение индуктивности

Источник



Индуктивное сопротивление катушки

Так как самоиндукция препятствует всякому резкому изменению силы тока в цепи, то, следовательно, она представляет собой для переменного тока особого рода сопротивление, называемое индуктивным сопротивлением. Чисто индуктивное сопротивление отличается от обычного (омического) сопротивления тем, что при прохождении через него переменного тока в нем не происходит потери мощности.

Под чисто индуктивным сопротивлением мы понимаем сопротивление, оказываемое переменному току катушкой, проводник которой не обладает вовсе омическим сопротивлением. В действительности же всякая катушка обладает некоторым омическим сопротивлением. Но если это сопротивление невелико по сравнению с индуктивным сопро¬тивлением, то им можно пренебречь.

При этом наблюдается следующее явление: в течение одной четверти периода, когда ток возрастает, магнитное поле потребляет энергию из цепи, а в течение следующей четверти периода, когда ток убывает, возвращает ее в цепь. Следовательно, в среднем за период в индуктивном сопротивлении мощность не затрачивается. Поэтому индуктивное сопротивление называется реактивным (прежде его неправильно называли безваттным).

Индуктивное сопротивление одной и той же катушки будет различным для токов различных частот. Чем выше частота переменного тока, тем большую роль играет индуктивность и тем больше будет индуктивное сопротивление данной катушки. Наоборот, чем ниже частота тока, тем индуктивное сопротивление катушки меньше. При частоте, равной нулю (установившийся постоянный ток), индуктивное сопротивление тоже равно нулю.

Рисунок 1. Зависимость индуктивного сопротивления катушки от частоты переменного тока. Реактивное сопротивление катушки возрастает с увеличением часторы тока.

Индуктивное сопротивление обозначается буквой XL и измеряется в омах.

Подсчет индуктивного сопротивления катушки для переменного тока данной частоты производится по формуле

XL=2π• f •L

где XL — индуктивное сопротивление в ом; f—частота переменного тока в гц; L — индуктивность катушки в гн

Как известно, величину 2π• f называют круговой частотой и обозначают буквой ω (омега). Поэтому приведенная выше формула может быть представлена так:

Отсюда следует, что для постоянного тока (ω = 0) индуктивное сопротивление равно нулю. Поэтому, когда, нужно пропустить по какой-либо цепи постоянный ток, задержав в то же время переменный, то в цепь включают последовательно катушку индуктивности.

Для преграждения пути токам низких звуковых частот ставят катушки с железным сердечником, так называемые дроссели низкой частоты, а для более высоких радиочастот — без железного сердечника, которые носят название дросселей высокой частоты.

Источник

Импеданс и квадруполи

Входное и выходное сопротивление

Квадруполь, нагруженный на выходе заданным импедансом нагрузки, ведет себя, если смотреть со своих входных клемм, как пассивный диполь, импеданс которого можно определить и измерить. Это называется квадрупольным входным сопротивлением .

Линия передачи

Характеристический импеданс в линии передачи идеальной (т.е. без потерь) определяется

Zпротивзнак равноLПРОТИВ{\ displaystyle Z_ {c} = {\ sqrt {\ frac {L} {C}}}}

где L и C — соответственно коэффициент самоиндукции или индуктивности и емкость на единицу длины линии. Это указано в каталогах производителей. Она зависит:

• размеры проводов и расстояние между ними;
• от диэлектрической проницаемости диэлектрика, в коаксиальной линии.

Типовые значения характеристического сопротивления:

• 50 или 75 Ом для коаксиальной линии  ;
• 300 Ом для двухпроводной линии .

Использование линии передачи — это в основном передача электроэнергии, которая с помощью соответствующей модуляции поддерживает информацию. Хорошая передача этой информации предполагает хорошую передачу энергии, которая предполагает хорошую адаптацию импедансов на входе и выходе кабеля. Эта хорошая адаптация происходит, когда полное сопротивление выводов равно характеристическому сопротивлению кабеля. В противном случае передача энергии не является полной, а непереданная энергия обращается, что имеет недостатки по отношению к желаемой цели. Вот почему было выбрано несколько значений характеристического импеданса, чтобы облегчить работу проектировщиков при использовании коаксиальных кабелей и их концевых заделок. (конструкция антенны, стандартные комплектующие)

Схематическое изображение элементарных компонентов линии передачи.

Для реальной линии передачи (с потерями) характеристический импеданс — это комплексное число  :

Zпротивзнак равнор+jωLграмм+jωПРОТИВ{\ displaystyle Z_ {c} = {\ sqrt {\ frac {R + j \ omega L} {G + j \ omega C}}}}

где R и G — соответственно сопротивление и проводимость потерь на единицу длины.

Мы замечаем, что на высокой частоте ( достаточно большой) R и G пренебрежимо малы спереди и, следовательно, хорошее приближение на реальной высокочастотной линии
ω{\ displaystyle \ scriptstyle {\ omega}}jωл{\ displaystyle \ scriptstyle {j \ omega l}}jωпротив{\ displaystyle \ scriptstyle {j \ omega c}}Zпротивзнак равноLПРОТИВ{\ displaystyle Z_ {c} = {\ sqrt {\ frac {L} {C}}}}

Практическое определение характеристического сопротивления: он зависит от физических параметров линии. Например, для коаксиального кабеля Zc зависит от соотношения диаметров внутреннего проводника и внешнего проводника, а также от диэлектрической проницаемости изолятора. Были приняты стандартизованные значения, поскольку они минимизируют потери Джоуля. Для напечатанной микрополосковой линии характеристический импеданс зависит от соотношения между шириной полосы (W), толщиной (h) изоляции между полосой и заземляющим слоем и диэлектрической проницаемостью изоляции.

Экспериментальные методы, основанные на измерении импеданса

Импедансная спектроскопия — общие сведения

Импедансная спектроскопия — это общий термин, который охватывает все методы, состоящие в измерении и анализе электрического импеданса образца, обычно как функции частоты, с целью получения информации о его физико-химических свойствах. Его также называют диэлектрической спектроскопией , когда он применяется к диэлектрическим материалам .

Медицинские приложения

Эти шкалы импеданса позволяют отделить массу жира и мышечную массу во время взвешивания. Сегодня коммерчески доступные, эти устройства используют различия в проводимости между этими разными тканями для отслеживания этой информации.

Pneumographie импеданс представляет собой метод для контроля движения дыхания (изменение объема легкого) изменением импеданса между электродами соответственно размещено.

Электрическая томографический представляет собой метод визуализации тела человека , с помощью которого изображение водостойкого в трех измерениях от нескольких измерений импеданса между электродами , расположенных на коже.

Похожие записи:

Диэлектрические средства защиты: перчатки, обувь, ковры Схема предварительного гитарного усилителя на полевых транзисторах Студийный свет: простые и мощные техники Можно ли за городом в обычном лесу обжигать бытовые провода для извлечения меди (цветных металлов) 9 схем подключения светодиодной ленты на 12 вольт Как измерять напряжение вольтметром