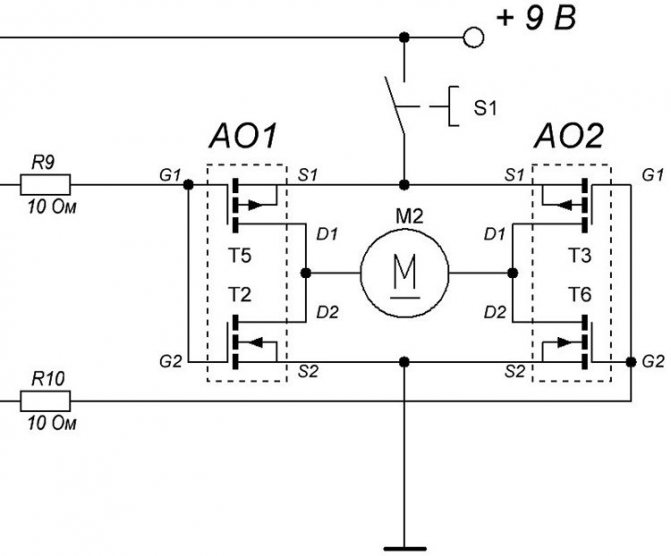
В распространенных формах волны
Синусоидальные , квадратные , треугольные и пилообразные формы сигналов. В каждом из них центральная линия находится на 0, положительный пик — на, а отрицательный — наузнак равноА1{\ displaystyle y = A_ {1}}узнак равно-А1{\ displaystyle y = -A_ {1}}
Прямоугольная импульсная волна с коэффициентом заполнения D, соотношением длительности импульса ( ) и периода (T); проиллюстрировано здесь с a = 1.τ{\ Displaystyle \ тау}
График зависимости напряжения синусоидальной волны от времени (в градусах), показывающий среднеквадратичное, пиковое (PK) и размах напряжения (PP).
Если форма волны представляет собой чистую синусоидальную волну , отношения между амплитудами (размах, пик) и среднеквадратичным значением фиксированы и известны, как и для любой непрерывной периодической волны. Однако это неверно для сигнала произвольной формы, который не может быть периодическим или непрерывным. Для синусоидальной волны с нулевым средним соотношение между среднеквадратичным значением и размахом амплитуды составляет:
- От пика до пика знак равно22×RMS≈2,8×RMS.{\ displaystyle = 2 {\ sqrt {2}} \ times {\ text {RMS}} \ примерно 2,8 \ times {\ text {RMS}}.}
Для других сигналов отношения не такие же, как для синусоидальных волн. Например, для треугольной или пилообразной волны
- От пика до пика знак равно23×RMS≈3.5×RMS.{\ displaystyle = 2 {\ sqrt {3}} \ times {\ text {RMS}} \ примерно 3,5 \ times {\ text {RMS}}.}
| Форма волны | Переменные и операторы | RMS |
|---|---|---|
| ОКРУГ КОЛУМБИЯ | узнак равноА{\ displaystyle y = A_ {0} \,} | А{\ displaystyle A_ {0} \,} |
| Синусоидальная волна | узнак равноА1грех(2πжт){\ Displaystyle у = А_ {1} \ грех (2 \ пи футов) \,} | А12{\ displaystyle {\ frac {A_ {1}} {\ sqrt {2}}}} |
| Квадратная волна | узнак равно{А1гидроразрыв(жт)<0,5-А1гидроразрыв(жт)>0,5{\ displaystyle y = {\ begin {cases} A_ {1} & \ operatorname {frac} (ft) <0,5 \\ — A_ {1} & \ operatorname {frac} (ft)> 0,5 \ end {cases}} } | А1{\ Displaystyle A_ {1} \,} |
| Прямоугольная волна со смещением постоянного тока | узнак равноА+{А1гидроразрыв(жт)<0,5-А1гидроразрыв(жт)>0,5{\ displaystyle y = A_ {0} + {\ begin {cases} A_ {1} & \ operatorname {frac} (ft) <0,5 \\ — A_ {1} & \ operatorname {frac} (ft)> 0,5 \ конец {case}}} | А2+А12{\ displaystyle {\ sqrt {A_ {0} ^ {2} + A_ {1} ^ {2}}} \,} |
| узнак равно{гидроразрыв(жт)<0,25А10,25<гидроразрыв(жт)<0,50,5<гидроразрыв(жт)<0,75-А1гидроразрыв(жт)>0,75{\ displaystyle y = {\ begin {cases} 0 & \ operatorname {frac} (ft) <0,25 \\ A_ {1} & 0,25 <\ operatorname {frac} (ft) <0,5 \\ 0 & 0,5 <\ operatorname {frac} (футы) <0,75 \\ — A_ {1} & \ operatorname {frac} (футы)> 0,75 \ end {case}}} | А12{\ displaystyle {\ frac {A_ {1}} {\ sqrt {2}}}} | |
| Треугольник волна | узнак равно|2А1гидроразрыв(жт)-А1|{\ displaystyle y = \ left | 2A_ {1} \ operatorname {frac} (ft) -A_ {1} \ right |} | А13{\ displaystyle A_ {1} \ over {\ sqrt {3}}} |
| Пилообразная волна | узнак равно2А1гидроразрыв(жт)-А1{\ displaystyle y = 2A_ {1} \ operatorname {frac} (ft) -A_ {1} \,} | А13{\ displaystyle A_ {1} \ over {\ sqrt {3}}} |
| Пульсовая волна | узнак равно{А1гидроразрыв(жт)<Dгидроразрыв(жт)>D{\ displaystyle y = {\ begin {cases} A_ {1} & \ operatorname {frac} (ft) <D \\ 0 & \ operatorname {frac} (ft)> D \ end {cases}}} | А1D{\ displaystyle A_ {1} {\ sqrt {D}}} |
| Междуфазное напряжение | узнак равноА1грех(т)-А1грех(т-2π3){\ displaystyle y = A_ {1} \ sin (t) -A_ {1} \ sin \ left (t — {\ frac {2 \ pi} {3}} \ right) \,} | А132{\ displaystyle A_ {1} {\ sqrt {\ frac {3} {2}}}} |
куда:
|
В комбинациях сигналов
Формы сигналов, полученные путем суммирования известных простых сигналов, имеют среднеквадратичное значение, которое является корнем из суммы квадратов значений компонентных среднеквадратичных значений, если формы сигналов компонентов ортогональны (то есть, если среднее значение произведения одного простого сигнала на другой равно нулю. для всех пар, кроме самого времени сигнала).
- RMSВсегознак равноRMS12+RMS22+⋯+RMSп2{\ displaystyle {\ text {RMS}} _ {\ text {Total}} = {\ sqrt {{\ text {RMS}} _ {1} ^ {2} + {\ text {RMS}} _ {2} ^ {2} + \ cdots + {\ text {RMS}} _ {n} ^ {2}}}}
В качестве альтернативы, для сигналов, которые полностью положительно коррелированы или «синфазны» друг с другом, их среднеквадратичные значения суммируются напрямую.
Как рассчитать Xc
Сила тока цепи с постоянными показателями напряжения в момент работы электроконденсатора равно 0. Ее значения в цепи с переменным напряжением после подключения конденсатора I ? 0. В итоге, цепочке с непостоянным напряжением конденсатор придает Xc меньшее, чем цепочке с неизменным показателем напряжения.
Формула вычисления показателя напряжения за одну секунду
Формула расчета величины силы электротока за мгновение
Получается, что изменения напряжения отличаются по фазе от изменений тока на π/2.
По закону, сформулированному Омом, показатели силы электротока находятся в прямой пропорциональной зависимости от величины напряжения цепи. Формула вычисления наибольших величин напряженности и силы тока:
Наибольшие величины напряженности и силы тока можно рассчитывать по формулеОкончательная формула расчета емкостного сопротивления в цепи переменного тока
ω = 2πf.
f — показатель частоты непостоянного тока, измеряется в герцах;
ω — показатель угловой частоты тока;
С — размер конденсатора в фарадах.
Важно! Xc не выступает параметром проводника, оно находится в зависимости от такой характеристики электроцепи, как частота электротока. Повышение значений данной величины вызывает рост пропускающей способности конденсатора (предел его сопротивления току непостоянному понижается). Повышение значений данной величины вызывает рост пропускающей способности конденсатора (предел его сопротивления току непостоянному понижается)
Повышение значений данной величины вызывает рост пропускающей способности конденсатора (предел его сопротивления току непостоянному понижается).
Представим, к цепи подключен конденсатор, емкостью 1 мкФ. Необходимо вычислить, уровень емкостного сопротивления при величине частоты 50 Гц и как изменится емкостное сопротивление цепи переменного тока при частоте 1 кГц. Амплитуда напряжения, подведенного к конденсатору, составляет 50 В.
После введения данных в формулу, определяющую Xc, и получаются значения:
Результат для частоты 50 ГцРезультат для 1 кГц
Емкостное сопротивление приравнивается к соотношению отклонений колебаний напряжения зажимов электрической цепочки с емкостными параметрами (с небольшими индуктивным и активным сопротивлениями) к колебаниям электротока цепочки. Она равнозначна электроконденсатору.
Что такое среднеквадратичный ток линии
Расчет среднего и среднеквадратичного значений тока и напряжения: формулы и калькулятор
Данный текст является расширенным и углубленным вариантом моей старой заметки на сайте we.easyelectronics.ru.
В рамках данной заметки рассмотрим способы вычисления среднего и среднеквадратичного значений тока и напряжения. При этом для простоты ограничимся формами сигнала, характерными для импульсных источников питания
Обращаю ваше внимание – все формулы, приводимые в заметке, даются без выводов, дабы не забивать головы читателей мутной и не особо нужной херней. С другой стороны, если кому-то интересно, откуда данные формулы взялись – можно скачать файл, в котором приведены все необходимые выводы с пояснениями
Будучи в недавнем прошлом яростным разработчиком всевозможных импульсных источников питания (ИИП), интересовался всяким по данной теме (да и сейчас, бывает, трясу стариной). В частности, весьма важными мне всегда казались такие характеристики сигнала, как среднее и среднеквадратичное значение токов и напряжений в различных точках схемы, поскольку при расчетах ИИП данные параметры используются сплошь и рядом. Чтобы понять, где могут быть полезны данные характеристики, сначала определимся с тем, что мы под ними понимаем.
Естественно, существуют строгие «математические» определения как для среднего, так и для среднеквадратичного значений физических величин, периодически изменяющихся во времени по некоторому закону. Однако, больно уж они мутные и абстрактные, и, на мой взгляд, нужны только при выводе формул. Разработчику же гораздо важнее понимать физический смысл используемых в расчетах величин, поэтому приводимые ниже определения среднего и среднеквадратичного значений будут носить сугубо прикладной характер.
Среднее значение переменного тока или напряжения (во вражеских терминах AVG) – это просто их постоянная составляющая. Поэтому вполне очевидно, что среднее значение широко применяется при расчетах схем, выделяющих из переменного сигнала постоянный уровень. Простейший понижающий преобразователь (Step-Down) с LC-фильтром на выходе, RC-цепочка, призванная выделить постоянное напряжение из поступающего на вход ШИМ-сигнала – всё это примеры того, где без использования среднего значения физической величины ничего толком не посчитаешь.
Среднеквадратичное (действующее, эффективное) значение определяется немного сложнее. Как известно, любой переменный ток (напряжение), проходя через активную линейную нагрузку (например, резистор), выделяет на ней некоторое количество тепла. Но так поступает не только переменный сигнал – постоянный ток тоже будет греть резистор.
Так вот, среднеквадратичное значение переменного тока или напряжения (во вражеских терминах RMS) – это такой постоянный ток (напряжение), который за одинаковый промежуток времени нагреет один и тот же резистор точно так же, как и исходный переменный сигнал. Поэтому одно из важнейших применений среднеквадратичного значения – расчет потерь и соответствующего нагрева для различных элементов силовых цепей ИИП. Хочешь узнать статические потери на ключе флайбэка – будь добр посчитать среднеквадратичное значение тока первички. Надо узнать мощность токосчитывающего резистора – туда же. Даже потери (и приблизительный нагрев) в обмотках трансов и дросселей для хиленьких источников и невысоких частот преобразования в первом приближении можно посчитать при помощи среднеквадратичного значения тока, через эти обмотки протекающего.
Обрыв нуля: как возникает и чем опасен
Нормальная работа электрооборудования происходит в сбалансированном режиме при нормально поданном напряжении на него. Если ноль пропадет, то бытовые приборы прекращают свою работу.
Здесь есть важные отличия при эксплуатации проводки, собранной по схеме однофазного или трехфазного питания.
Обрыв нуля в однофазной сети: опасность возникновения
Квартирная проводка подключается для подачи напряжения по двум проводам с потенциалами фазы и нуля (контура земли). Электрический ток нагрузки, совершающий полезную работу, может протекать только по замкнутому контуру.
Это значит, что если один потенциал от обмотки трансформаторной подстанции не будет подведен к розетке или лампочке в квартире, то на них напряжения, а, следовательно, и работы не будет.
Однако здесь есть особенность, связанная с безопасностью жильцов.
Обычно розеточные группы собираются шлейфом при параллельном подключении между собой. В одну из них может быть вставлена вилка шнура питания какого-то прибора: холодильника, стиральной машины, микроволновки и т п.
В такой ситуации через внутреннюю схему этого прибора потенциал фазы пройдет на контакт нуля розетку и дальше — к концу подключенного, но оборванного провода.
Электрики говорят по этому поводу: две фазы в розетке! Их легко заметить однофазным индикатором напряжения. Его контрольная лампочка будет светиться в обоих контактных гнездах.
Этот режим опасен тем, что оторванный конец не изолирован. Под действие вновь образованного потенциала может попасть человек, получить электрическую травму.
Генерирование переменного тока[править]
Простейший генератор переменного тока: если вокруг проволочной катушки, намотанной на магнитопровод из трансформаторной стали вращать маховик с установленными в нём несколькими парами постоянных магнитов, то в катушке (условно показан один виток) будет наводиться синусоидальная ЭДС, а при подключении нагрузки в электрической цепи появится переменный ток.Применяется на транспортных средствах (мопеды, лёгкие мотоциклы, снегоходы, гидроциклы, а также на подвесных лодочных моторах), работает совместно с выпрямителем и регулятором напряжения (см. магдино).
Основная статья: Генератор переменного тока
Принцип действия генератора переменного тока основан на законе электромагнитной индукции — индуцировании электродвижущей силы в прямоугольном контуре (проволочной рамке), находящейся в однородном вращающемся магнитном поле.
Электродвижущая сила генератора переменного тока определяется по формуле:
, где
— количество витков;
— магнитная индукция магнитного поля в вольт-секундах на квадратный метр (Тл, Тесла);
— длина каждой из активных сторон контура в метрах;
— угловая скорость синусоидальной электродвижущей силы, в данном случае равная угловой скорости вращения магнита в контуре;
— фаза синусоидальной электродвижущей силы.
Частота переменного тока, вырабатываемого генератором, определяется по формуле:
, где
— частота в герцах;
— число оборотов ротора в минуту;
— число пар полюсов.
По количеству фаз генераторы переменного тока бывают:
- трёхфазные генераторы — основной тип мощных промышленных генераторов;См. также трёхфазная система электроснабжения, трёхфазный двигатель, автомобильный генератор трёхфазного переменного тока.
- однофазные генераторы, применяются, как правило, на маломощных бензиновых электростанциях, встроены в двигатели внутреннего сгорания мопедов, лёгких мотоциклов, снегоходов, гидроциклов, подвесные лодочные моторы;См. также конденсаторный двигатель, однофазный двигатель.
- двухфазные генераторы, встречаются значительно реже по сравнению с однофазными и трёхфазными.См. также двухфазная электрическая сеть, двухфазный двигатель.
Модифицированная синусоида, генерируемая инвертором.
Инверторыправить
Постоянный ток может быть преобразован в переменный с помощью инвертора.
Следует отметить, что недорогие модели инверторов имеют на выходе переменный ток несинусоидальной формы, обычно прямоугольные импульсы или модифицированная синусоида. Для получения синусоидального тока инвертор должен иметь задающий генератор (как правило, специализированная микросхема, формирующая электрический сигнал синусоидальной формы, который затем управляет работой тиристорных или транзисторных электронных ключей.
Фазорасщепительправить
Трёхфазный ток может быть получен из однофазного при помощи фазорасщепителя. Эти электрические машины применяются, в частности, на электровозах, таких как ВЛ60, ВЛ80.
Поведение конденсатора в цепи переменного тока
Если говорить строго, то через конденсатор не проходит ни постоянный, ни переменный ток, так как между обкладками находится изолятор, в котором свободные электрические заряды двигаться не могут.
Включение конденсатора в цепь постоянного тока равносильно разрыву этой цепи. Что же касается переменного тока, то он будет протекать по цепи, в которую включен конденсатор, благодаря периодическому заряду и разряду этого конденсатора. Действительно, когда происходит заряд конденсатора, то электрические заряды, например электроны, на одной обкладке накапливаются, а с другой обкладки уходят. При этом они, конечно, двигаются по соединительным проводам, подключенным к обкладкам конденсатора. Такое же движение зарядов, только в противоположном направлении, происходит и при разряде конденсатора.
Если включить конденсатор в цепь переменного тока, то он будет периодически заряжаться то в одной полярности, то в противоположной. Это значит, что электроны будут накапливаться то на одной, то на другой обкладке, и каждый раз при заряде и разряде свободные электроны будут двигаться по цепи, в которую включен конденсатор, не попадая, однако, в изолятор, включенный между обкладками. А поскольку под действием переменного напряжения в цепи конденсатора двигаются заряды, то мы считаем, что конденсатор пропускает переменный ток, хотя и в этом случае заряды не проходят через изолятор.
Конденсатор влияет на величину переменного тока в цепи, и поэтому (по аналогии с законом Ома) его часто рассматривают как сопротивление. Это так называемое емкостное сопротивление обозначается буквой хс и так же, как и обычное сопротивление, измеряется в омах. Величина хс зависит от частоты переменного тока и от емкости С конденсатора: с уменьшением емкости конденсатора, так же как и с уменьшением частоты переменного тока, емкостное сопротивление конденсатора увеличивается (рис. 80, 81, лист 87). Эту зависимость удобно записать в виде простой формулы:
Смысл этой формулы весьма прост: чем меньше емкость С, тем меньше зарядов будет двигаться к обкладкам при каждом заряде и разряде конденсатора; чем меньше частота переменного тока, тем реже будет заряжаться и разряжаться конденсатор. Отсюда следует, что с уменьшением f и С уменьшается ток в цепи, или, иными словами, растет сопротивление конденсатора.
Этот вывод имеет огромное практическое значение. Так, например, если нам понадобится включить в цепь конденсатор с очень маленьким емкостным сопротивлением, то емкость этого конденсатора нужно будет выбирать с учетом частоты переменного тока в цепи. Для высоких частот можно будет взять конденсатор небольшой емкости, а вот для низких частот емкость конденсатора придется взять большой. Это хорошо иллюстрируется простым примером. На частоте 100 кгц конденсатор емкостью 100 пф обладает емкостным сопротивлением хс=16 ком. При уменьшении частоты в 1000 раз, то есть на частоте 100 гц, сопротивление конденсатора возрастет в 1000 раз и станет равным 16 000 ком (16 Мом). Для того чтобы при уменьшении частоты емкостное сопротивление не изменилось, нужно увеличить емкость конденсатора. Сопротивление 16 ком на частоте 100 гц будет иметь конденсатор емкостью 100 000 пф (0,1 мкф).
Из приведенной выше формулы следует также, что уменьшение емкости конденсатора связи Ссв (лист 85) приведет к росту сопротивления этого конденсатора, а следовательно, к уменьшению тока в цепи антенны. Поэтому емкость Ссв нельзя брать слишком малой.
Сказанное можно пояснить еще иначе. Конденсатор связи и колебательный контур Lк Ск можно рассматривать как делитель напряжения, к которому приложена э. д. с, действующая между зажимами А («антенна») и З («земля»). Мы не будем пока говорить о том, чему равно сопротивление колебательного контура – даже без этого ясно: чем больше емкостное сопротивление конденсатора связи, тем меньшая часть э. д. с. будет действовать на нижней части делителя – на контуре и подключенной к нему цепи детектор – телефон.
Читать дальше – Трансформаторная связь
Параметры переменного тока и напряжения
Величина переменного тока, как и напряжения, постоянно меняется во времени. Количественными показателями для измерений и расчётов применяются их следующие параметры:
ПериодT — время, в течении которого происходит один полный цикл изменения тока в оба направления относительно нуля или среднего значения.
Частотаf — величина, обратная периоду, равная количеству периодов за одну секунду. Один период в секунду это один герц (1 Hz)
f =
1/TЦиклическая частотаω — угловая частота, равная количеству периодов за2π секунд.
ω = 2πf = 2π/T
Обычно используется при расчётах тока и напряжения синусоидальной формы. Тогда в пределах периода можно не рассматривать частоту и время, а исчисления производить в радианах или градусах. T = 2π = 360°
Начальная фазаψ — величина угла от нуля (ωt = 0) до начала периода. Измеряется в радианах или градусах. Показана на рисунке для синего графика синусоидального тока.
Начальная фаза может быть положительной или отрицательной величиной, соответственно справа или слева от нуля на графике.
Мгновенное значение
— величина напряжения или тока измеренная относительно нуля в любой выбранный момент времениt .
i = i(t); u = u(t)
Последовательность всех мгновенных значений в любом интервале времени можно рассмотреть как функцию изменения тока или напряжения во времени. Например, синусоидальный ток или напряжение можно выразить функцией:
i = I ampsin(ωt); u = U ampsin(ωt)
С учётом начальной фазы:
i = I ampsin(ωt + ψ); u = U ampsin(ωt + ψ)
Здесь I amp
иU amp — амплитудные значения тока и напряжения.
Амплитудное значение
— максимальное по модулю мгновенное значение за период.
I amp = max|i(t)|; U amp = max|u(t)|
Может быть положительным и отрицательным в зависимости от положения относительно нуля. Часто вместо амплитудного значения применяется термин амплитуда
тока (напряжения) — максимальное отклонение от нулевого значения.
Среднее значение
(avg) — определяется как среднеарифметическое всех мгновенных значений за периодT .
Среднее значение является постоянной составляющей DC
напряжения и тока. Для синусоидального тока (напряжения) среднее значение равно нулю.
Средневыпрямленное значение
— среднеарифметическое модулей всех мгновенных значений за период.
Для синусоидального тока или напряжения средневыпрямленное значение равно среднеарифметическому за положительный полупериод.
Среднеквадратичное значение (rms) — определяется как квадратный корень из среднеарифметического квадратов всех мгновенных значений за период.
Для синусоидального тока и напряжения амплитудой I amp
(U amp ) среднеквадратичное значение определится из расчёта:
Среднеквадратичное — это действующее, эффективное значение, наиболее удобное для практических измерений и расчётов. Является объективным количественным показателем для любой формы тока. В активной нагрузке переменный ток совершает такую же работу за время периода, что и равный по величине его среднеквадратичному значению постоянный ток.
Расчет силы тока по мощности, напряжению, сопротивлению
Бесплатный калькулятор расчета силы тока по мощности и напряжению/сопротивлению – рассчитайте силу тока в однофазной или трехфазной сети в ОДИН КЛИК!
Если вы хотите узнать как рассчитать силу тока в цепи по мощности, напряжению или сопротивлению, то предлагаем воспользоваться данным онлайн-калькулятором. Программа выполняет расчет для сетей постоянного и переменного тока (однофазные 220 В, трехфазные 380 В) по закону Ома. Рекомендуем без необходимости не изменять значение коэффициента мощности (cos φ) и оставлять равным 0.95. Знание величины силы тока позволяет подобрать оптимальный материал и диаметр кабеля, установить надежные предохранители и автоматические выключатели, которые способны защитить квартиру от возможных перегрузок. Нажмите на кнопку, чтобы получить результат.
Смежные нормативные документы:
- СП 256.1325800.2016 «Электроустановки жилых и общественных зданий. Правила проектирования и монтажа»
- СП 31-110-2003 «Проектирование и монтаж электроустановок жилых и общественных зданий»
- СП 76.13330.2016 «Электротехнические устройства»
- ГОСТ 31565-2012 «Кабельные изделия. Требования пожарной безопасности»
- ГОСТ 10434-82 «Соединения контактные электрические. Классификация»
- ГОСТ Р 50571.1-93 «Электроустановки зданий»
Генерирование переменного тока[править]
Простейший генератор переменного тока: если вокруг проволочной катушки, намотанной на магнитопровод из трансформаторной стали вращать маховик с установленными в нём несколькими парами постоянных магнитов, то в катушке (условно показан один виток) будет наводиться синусоидальная ЭДС, а при подключении нагрузки в электрической цепи появится переменный ток.Применяется на транспортных средствах (мопеды, лёгкие мотоциклы, снегоходы, гидроциклы, а также на подвесных лодочных моторах), работает совместно с выпрямителем и регулятором напряжения (см. магдино)
Основная статья: Генератор переменного тока
Принцип действия генератора переменного тока основан на законе электромагнитной индукции — индуцировании электродвижущей силы в прямоугольном контуре (проволочной рамке), находящейся в однородном вращающемся магнитном поле.
Электродвижущая сила генератора переменного тока определяется по формуле:
, где
— количество витков;
— магнитная индукция магнитного поля в вольт-секундах на квадратный метр (Тл
,Тесла );
— длина каждой из активных сторон контура в метрах;
— угловая скорость синусоидальной электродвижущей силы, в данном случае равная угловой скорости вращения магнита в контуре;
— фаза синусоидальной электродвижущей силы.
Частота переменного тока, вырабатываемого генератором, определяется по формуле:
, где
— частота в герцах;
— число оборотов ротора в минуту;
— число пар полюсов.
По количеству фаз генераторы переменного тока бывают:
- трёхфазные генераторы — основной тип мощных промышленных генераторов;См. также трёхфазная система электроснабжения, трёхфазный двигатель, автомобильный генератор трёхфазного переменного тока .
- однофазные генераторы, применяются, как правило, на маломощных бензиновых электростанциях, встроены в двигатели внутреннего сгорания мопедов, лёгких мотоциклов, снегоходов, гидроциклов, подвесные лодочные моторы;См. также конденсаторный двигатель, однофазный двигатель .
- двухфазные генераторы, встречаются значительно реже по сравнению с однофазными и трёхфазными.См. также двухфазная электрическая сеть, двухфазный двигатель .
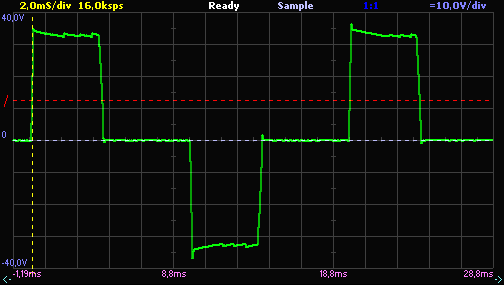
Модифицированная синусоида, генерируемая инвертором.
Инверторыправить
Постоянный ток может быть преобразован в переменный с помощью инвертора.
Следует отметить, что недорогие модели инверторов имеют на выходе переменный ток несинусоидальной формы, обычно прямоугольные импульсы или модифицированная синусоида. Для получения синусоидального тока инвертор должен иметь задающий генератор (как правило, специализированная микросхема, формирующая электрический сигнал синусоидальной формы, который затем управляет работой тиристорных или транзисторных электронных ключей.
Фазорасщепительправить
Трёхфазный ток может быть получен из однофазного при помощи фазорасщепителя. Эти электрические машины применяются, в частности, на электровозах, таких как ВЛ60, ВЛ80.