Расчет резистора для светодиода: как правильно рассчиатть и подобрать сопротивление для светодиода в сети на 12 вольт, какая нужна формула, пример расчета ограничительного резистора

Расчет резистора для светодиода

Надежная работа светодиода зависит от тока, протекающего через него. При заниженных значениях, он просто не будет светить, а при превышении значения тока – характеристики элемента ухудшатся, вплоть до его разрушения. При этом говорят – светодиод сгорел. Для того чтобы исключить возможность выхода из строя этого полупроводника необходимо подобрать в цепь с включенным в нее, резистором. Он будет ограничивать ток в цепи на оптимальных значениях.

Вычисление номинала сопротивления

Для работы радиоэлемента на него нужно подать питание. По закону Ома, чем больше сопротивление отрезка цепи, тем меньший ток по нему протекает. Опасная ситуация возникает, если в схеме течет больший ток, чем положено, так как каждый элемент не выдерживает большей токовой нагрузки.

Сопротивление светодиода является нелинейным. Это значит, что при изменении напряжения, подаваемого на этот элемент, ток, протекающий через него, будет меняться нелинейно. Убедиться в этом можно, если найти вольт — амперную характеристику любого диода, в том числе и светоизлучающего. При подаче питания ниже напряжения открытия p – n перехода, ток через светодиод низкий, и элемент не работает. Как только этот порог превышен, ток через элемент стремительно возрастает, и он начинает светиться.

https://youtube.com/watch?v=hHZIrgozdHw

Если источник питания соединять непосредственно со светодиодом, диод выйдет из строя, так как не рассчитан на такую нагрузку

Чтобы этого не произошло – нужно ограничить ток, протекающий через светодиод балластным сопротивлением, или произвести понижение напряжения на важном для нас полупроводнике

https://youtube.com/watch?v=yEHgznYygDY

Рассмотрим простейшую схему подключения (рисунок 1). Источник питания постоянного тока подключается последовательно через резистор к нужному светодиоду, характеристики которого нужно обязательно узнать. Сделать это можно в интернете, скачав описание (информационный лист) на конкретную модель, или найдя нужную модель в справочниках. Если найти описание не представляется возможным, можно приблизительно определить падение напряжения на светодиоде по его цвету:

Инфракрасный — до 1.9 В.
Красный – от 1.6 до 2.03 В.
Оранжевый – от 2.03 до 2.1 В.
Желтый – от 2.1 до 2.2 В.
Зеленый – от 2.2 до 3.5 В.
Синий – от 2.5 до 3.7 В.
Фиолетовый – 2.8 до 4 В.
Ультрафиолетовый – от 3.1 до 4.4 В.
Белый – от 3 до 3.7 В.

Рисунок 1 – схема подключения светодиода

Ток в схеме можно сравнить с движением жидкости по трубе. Если есть только один путь протекания, то сила тока (скорость течения) во всей цепи будет одинакова. Именно так происходит в схеме на рисунке 1. Согласно закону Кирхгоффа, сумма падений напряжения на всех элементах, включенных в цепь протекания одного тока, равно ЭДС этой цепи (на рисунке 1 обозначено буквой Е). Отсюда можно сделать вывод, что напряжение, падающее на токоограничивающем резисторе должно быть равным разности напряжения питания и падения его на светодиоде.

Так как ток в цепи должен быть одинаковым, то и через резистор, и через светодиод ток получается одним и тем же. Для стабильной работы полупроводникового элемента, увеличения его показателей надежности и долговечности, ток через него должен быть определенных значений, указанных в его описании. Если описание найти невозможно, можно принять приблизительное значение тока в цепи 10 миллиампер. После определения этих данных уже можно вычислить номинал сопротивления резистора для светодиода. Он определяется по закону Ома. Сопротивление резистора равно отношению падения напряжения на нем к току в цепи. Или в символьной форме:

R = U (R)/ I,

где, U (R) — падение напряжения на резисторе

I – ток в цепи

Расчет U (R) на резисторе:

U (R) = E – U (Led )

где, U (Led) — падение напряжения на светодиодном элементе.

С помощью этих формул получится точное значение сопротивления резистора. Однако, промышленностью выпускаются только стандартные значения сопротивлений так называемые ряды номиналов. Поэтому после расчета придется сделать подбор существующего номинала сопротивления. Подобрать нужно чуть больший резистор, чем получилось в расчете, таким образом, получится защита от случайного превышения напряжения в сети. Если подобрать близкий по значению элемент сложно, можно попробовать соединить два резистора последовательно, или параллельно.

Подбор мощности резистора

Если подобрать сопротивление меньшей мощности, чем нужно в схеме, оно просто выйдет из строя. Расчет мощности резистора довольно прост, нужно падение напряжения на нём умножить на ток, протекающий в этой цепи. После чего нужно выбрать сопротивление с мощностью, не меньшей рассчитанной.

https://youtube.com/watch?v=MrsDSqIAun8

Базовые «теоретические» предпосылки

Формула была получена в предположении того, что в металле (из которого состоит нить накаливания) ток и сопротивление имеют единую физическую сущность.

В упрощенном виде это можно рассуждать примерно так.

Сообразно современным воззрениям, ток представляет собой упорядоченное движение носителей заряда. Для металла это будут электроны.

Было сделано предположение, что электрическое сопротивление металла определяется ХАОТИЧЕСКИМ движением тех же самых электронов.

С возрастанием температуры нити, хаотическое движение электронов возрастает, что, в конечном итоге, и приводит к возрастанию электрического сопротивления.

Еще раз. Ток и сопротивление в нити накаливания – суть одно и тоже. С той лишь разницей, что ток – это упорядоченное движение под действием электрического поля, а сопротивление – это хаотическое движение электронов.

Проверка дуговой ртутной лампы

Светильник с дуговой ртутной люминофорной лампой (ДРЛ) обычно можно встретить на улице или в заводском цехе. Для определения работоспособности прозванивают дроссель – устройство, ограничивающее ток, питающий ДРЛ.

Если схема была разорвана, то сопротивление будет неограниченно большим, что и покажет прибор. Если имеется потеря изоляции, ведущая к короткому замыканию, показатель повышается незначительно. В случае наличия замыкания в обмотке дросселя, сопротивление не меняется.

Если при проверке тестером дросселя проблем не было выявлено, то дуговая лампочка может не функционировать по причине неисправностей в системе подачи электроэнергии, к примеру, из-за окисления контактов. Принцип работы светильника очень простой, поэтому неисправности непосредственно в лампе ДРЛ встречаются редко.

Работа с сетью 220 В

Самый простой указатель напряжения электросети без источника питания делается из резистора, ограничителя тока (транзистора), выпрямителя (диода) и любого светодиода. Сопротивление резистора 100 – 150 кОм.

Характеристики диода:

ток
10-100 мА;
напряжение
1-1,1 В;
обратное
напряжение 30-75 В.

При 220 В частоте 3 Гц светодиод
загорается. Корректировать частоту и повысить яркость можно изменением емкости
конденсатора. Такой индикатор срабатывает при минимальном напряжении 4,5 В.
Кроме тока сети он может определить исправность, включенное и выключенное
состояние электроприбора.

https://youtube.com/watch?v=t7Zz8IGAda4

Проверка
постоянного напряжения

Для проверки сети на 12 вольт и целостности соединений можно сделать другой светодиодный индикатор (нужны 2 разноцветных светодиодных элемента). Для ограничения тока можно использовать резистор с сопротивлением 50-100 Ом или лампочку накаливания с небольшой мощностью. Один из светодиодов загорается при подключении напряжения соответствующей полярности.

В самодельный индикатор для сети 12 В можно добавить конденсатор, диод и 2 транзистора. Полевой транзистор стабилизирует ток. Конденсатор, защищающий диод от скачков напряжения, нужен с емкостью 0,1 мкФ, неполярный. Резистор с сопротивлением 1 Мом является нагрузкой биполярного транзистора. При проверке сети с постоянным напряжением диод проверяет полюса. Если ток переменный, этот элемент срезает минусовую половину. При подаче напряжения значение тока определяет биполярный транзистор и сопротивление резистора (500-600 Ом).

Такой прибор подходит для работы с переменной и постоянной сетью с напряжением 5-600 В.

Индикатор
для микросхем – логический пробник

Приборы для индикации микросхем называются логическими пробниками. Такой индикатор трехуровневый (в схему включаются 3 светодиода).

Логический пробник дает возможность:

определить
фазу, короткое замыкание, сопротивление электросети;
установить
наличие напряжения 12 – 400 В;
определить
полюса при постоянном токе;
проверить
состояние диодов, транзисторов и других деталей;
определить
целостность электросети прозвоном;
диагностировать
обрывы реле и катушек;
прозвонить
дроссели и моторы;
определить
выводы трансформаторов.

Источник питания батарейка на 9 В. При
замкнутых щипах потребляется ток 110 мА. После размыкания ток не потребляется,
устанавливать выключатель и переключатель режимов не нужно.

При проверке сети с сопротивлением 0 –
150 Ом горят 2 светодиода, при повышении показателя один. При 220-380 вольтах
загорается третий, остальные мерцают. Если цепь порвана, светодиоды не
загораются. При нуле на контакте 0,5 В, открывается один транзистор (КТ315Б),
при 2,4 В – второй (КТ203Б).

Допускается замена транзисторов на другие, имеющие аналогичные параметры.

https://youtube.com/watch?v=et-JVs6Xhs4

Индикатор
напряжения на двухцветном светодиоде

Еще одна простая микросхема индикатора – с двухцветным светодиодом. Некоторые домашние мастера используют ее для определения режима работы лампы. Например, выключатель осветительного прибора в подвале, оснащенный индикатором, установлен на лестнице. Если она горит, свечение красное, после выключения – зеленое.

Вариант
для автомобиля

Схема
для индикации заряда аккумулятора и напряжения сети автомобиля состоит из:

RGB-светодиода;
3-х
стабилитронов;
3-х
биполярных транзисторов (BC847C);
9-и
резисторов;

Уровень определяется по цвету. Зеленое свечение при 12-14 В, синее – при 11,5 В, красное – при 14,4 В).

Если при сборке схемы не допущены ошибки, один из резисторов (на 2,2 кОм) и транзистор (на 8,2 В) определяют минимальный предел вольтажа. При снижении показателя транзистор, соответствующий синему свечению, подключает кристалл.

Если вольтаж не снижается и не повышается, ток проходит через 2 резистора, стабилитрон на 5,6 В и светодиод, появляется свечение зеленого цвета (транзисторы, соответствующие красному и синему цвету, закрываются). При повышении напряжения до 14,4 В загорается красный свет.

https://youtube.com/watch?v=s8VkBj2_EeA

Схема с балластным сопротивлением

Для случая, когда лампа включается последовательно с балластным резистором, для расчета напряжение на ней необходимо решить простенькое квадратное уравнение приведенного вида:

U + ( Rрезист / Sлампы) * корень(U) = U питания.

Вывод формулы с балластным сопротивлением

На рисунке представлен порядок вывода формулы для случая, когда лампа последовательно соединена с балластным сопротивлением. Ток через лампу и через сопротивление одинаков.

Выражения для токов приравниваются. Небольшие алгебраические преобразования. И получается окончательное квадратное уровнение относительно неизвестного Us.

Из рисунка понятно, что Us это напряжение на лампе.

Закон Ома для цепи

Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит. Возьмем замкнутую электрическую цепь и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).

Итак, закон Ома для рассматриваемого участка цепи имеет вид:

φ1-φ2=I*R, где

I – ток, протекающий по участку цепи.
R – сопротивление этого участка.
φ1-φ2 – разность потенциалов между точками 1-2.

Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R. Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).

В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:

U1=I*R1
U2=I*R2
Un=I*Rn
U=I*(R1+R2+…+Rn

Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:

U=U1+U2+…+Un или U1/U2/…/Un=R1/R2/…/Rn

Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.

Закон Ома для участка цепи.

Для ЭДС

Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.

Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.

Для полной цепи

Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.

Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.

Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:

I = U / (R + r)

Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.

Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.

https://youtube.com/watch?v=f2rpF5ztAr0

ФИЗИКА

§ 45. Расчёт сопротивления проводника. Удельное сопротивление

Мы знаем, что причиной электрического сопротивления проводника является взаимодействие электронов с ионами кристаллической решётки металла (§ 43). Поэтому можно предположить, что сопротивление проводника зависит от его длины и площади поперечного сечения, а также от вещества, из которого он изготовлен.

На рисунке 74 изображена установка для проведения такого опыта. В цепь источника тока по очереди включают различные проводники, например:

никелиновые проволоки одинаковой толщины, но разной длины;
никелиновые проволоки одинаковой длины, но разной толщины (разной площади поперечного сечения);
никелиновую и нихромовую проволоки одинаковой длины и толщины.

Силу тока в цепи измеряют амперметром, напряжение — вольтметром.

Зная напряжение на концах проводника и силу тока в нём, по закону Ома можно определить сопротивление каждого из проводников.

Рис. 74. Зависимость сопротивления проводника от его размеров и рода вещества

Выполнив указанные опыты, мы установим, что:

из двух никелиновых проволок одинаковой толщины более длинная проволока имеет большее сопротивление;
из двух никелиновых проволок одинаковой длины большее сопротивление имеет проволока, поперечное сечение которой меньше;
никелиновая и нихромовая проволоки одинаковых размеров имеют разное сопротивление.

Зависимость сопротивления проводника от его размеров и вещества, из которого изготовлен проводник, впервые на опытах изучил Ом. Он установил, что сопротивление прямо пропорционально длине проводника, обратно пропорционально площади его поперечного сечения и зависит от вещества проводника.

Как учесть зависимость сопротивления от вещества, из которого изготовляют проводник? Для этого вычисляют так называемое удельное сопротивление вещества.

Удельное сопротивление — это физическая величина, которая определяет сопротивление проводника из данного вещества длиной 1 м, площадью поперечного сечения 1 м2.

Введём буквенные обозначения: ρ — удельное сопротивление проводника, I — длина проводника, S — площадь его поперечного сечения. Тогда сопротивление проводника R выразится формулой

Из неё получим, что:

Из последней формулы можно определить единицу удельного сопротивления. Так как единицей сопротивления является 1 Ом, единицей площади поперечного сечения — 1 м2, а единицей длины — 1 м, то единицей удельного сопротивления будет:

Удобнее выражать площадь поперечного сечения проводника в квадратных миллиметpax, так как она чаще всего бывает небольшой. Тогда единицей удельного сопротивления будет:

В таблице 8 приведены значения удельных сопротивлений некоторых веществ при 20 °С. Удельное сопротивление с изменением температуры меняется. Опытным путём было установлено, что у металлов, например, удельное сопротивление с повышением температуры увеличивается.

Таблица 8. Удельное электрическое сопротивление некоторых веществ (при t = 20 °С)

Из всех металлов наименьшим удельным сопротивлением обладают серебро и медь. Следовательно, серебро и медь — лучшие проводники электричества.

При проводке электрических цепей используют алюминиевые, медные и железные провода.

Во многих случаях бывают нужны приборы, имеющие большое сопротивление. Их изготавливают из специально созданных сплавов — веществ с большим удельным сопротивлением. Например, как видно из таблицы 8, сплав нихром имеет удельное сопротивление почти в 40 раз большее, чем алюминий.

Фарфор и эбонит имеют такое большое удельное сопротивление, что почти совсем не проводят электрический ток, их используют в качестве изоляторов.

Вопросы

Как зависит сопротивление проводника от его длины и от площади поперечного сечения?
Как показать на опыте зависимость сопротивления проводника от его длины, площади поперечного сечения и вещества, из которого он изготовлен?
Что называется удельным сопротивлением проводника?
По какой формуле можно рассчитывать сопротивление проводников?
В каких единицах выражается удельное сопротивление проводника?
Из каких веществ изготавливают проводники, применяемые на практике?

Проверяем лампу накаливания

Для проверки лампочки ее можно ввинтить в другую люстру или фонарик. Однако это не во всех случаях можно сделать. Иногда диаметр цоколя лампочки отличается от разъема на светильнике либо в доме больше нет устройств с аналогичным патроном.

Лампы накаливания на 220 В работают в сетях переменного тока, поэтому полярность при их прозвонке не важна.

В режиме прозвонки

Чтобы узнать, работает ли лампочка, с помощью тестера, сначала нужно установить на нем соответствующий режим. После этого одним измерительным щупом нужно дотронуться до контакта в центре обыкновенной или галогеновой лампы, а другим – до контакта на резьбе цоколя.

Как проверить лампочку мультиметром?

Не всегда визуальный осмотр лампы позволяет сделать вывод о её пригодности или непригодности. Бывают случаи, когда вольфрамовая нить не имеет повреждений, но лампочка в светильнике не светится. Еще сложнее дела обстоят со светодиодными или люминесцентными лампами. Установить причину и тем самым подтвердить или опровергнуть неисправность лампы можно несколькими способами. О том, как это сделать, можно узнать из этой статьи.

Простейший способ

Самый простой способ диагностики подходит как для лампочек накаливания, так и для люминесцентных и светодиодных ламп. Он предполагает вкрутить подозрительную лампочку в другой светильник и включить его. К сожалению, это не всегда возможно. Иногда резьбовая часть цоколя изготовлена с отклонением от стандартного размера и при вкручивании в патрон не замыкает оба электрических контакта. Или в доме больше нет светильников с точно таким же патроном.

Покупая лампочку в магазине электротоваров, многие обращали внимание на то, как продавец проверяет её с помощью тестера. В корпусе тестера есть несколько разъёмов, предназначенных для диагностики лампочек разного типа: накаливания, люминесцентных и галогенных

Его задача – проверить целостность проводников внутри лампы, о чём свидетельствует звуковой сигнал. Эту же самую операцию можно проделать в домашних условиях, воспользовавшись мультиметром или многофункциональной индикаторной отвёрткой.

В режиме прозвонки

Каждый мультиметр имеет режим прозвонки, с помощью которого можно проверить целостность электрического соединения. На панели прибора данный режим обозначается специальным символом. Чтобы проверить работоспособность лампочки нужно:

установить переключатель в режим прозвонки (проверки на обрыв);
коснуться одним щупом центрального контакта, а другим – бокового (для ламп накаливания с резьбовым цоколем).

Если осветительный прибор исправен, то тестер издаёт звук, а на ЖК-дисплее появляется число в пределах 3-200 Ом.

Перед каждым измерением следует кратковременно замыкать щупы между собой, чтобы убедиться в исправности измерительной цепи тестера.

Компактную люминесцентную (КЛЛ) и светодиодную лампу таким способом не протестируешь, из-за наличия внутри электронной схемы. Отдельно можно проверить пригодность только стеклянную спираль КЛЛ. Для этого её нужно аккуратно отделить от цокольной части и прозвонить две пары проволочных выводов, идущих на плату электронного балласта.

В режиме проверки сопротивления

Существует ещё один, более точный, метод диагностики спиральных ламп с помощью мультиметра. Им можно не только определить пригодность лампочки, но и узнать её сопротивление. Зачем это нужно? Например, заводской отпечаток на колбе лампы накаливания стёрт. Следовательно, её мощность неизвестна. Данный способ поможет решить эту проблему.

Теперь о том, как проверить лампочку мультиметром в режиме сопротивления. Для этого нужно перевести переключатель на позицию с пределом 200 Ом, а затем коснуться щупами электрических контактов лампы точно так же, как в режиме прозвонки. В этом случае звуковой сигнал отсутствует, а на ЖК-дисплее появится значение сопротивления в Омах. Если на табло осталась «1», то внутри осветительного прибора обрыв.

По измеренному сопротивлению спирали в холодном состоянии можно сделать вывод о её мощности. В нами составленной таблице приведены данные об основных типах ламп, применяемых в быту.

Во время замера следует помнить, что за счёт плохого контакта щупов с тестером полученный результат может отличаться от табличного в большую сторону на несколько Ом.

Проверка индикаторной отверткой

Чтобы в домашних условиях проверить на исправность лампочку, необязательно иметь под рукой мультиметр. Гораздо быстрее это сделать с помощью многофункциональной индикаторной отвёртки. Её отличие от обычного индикатора заключается в наличии батарейки-таблетки внутри корпуса. Работоспособность такой отвертки проверяется касанием пальцев её металлических контактов с торцов. При этом индикаторный светодиод внутри неё должен светиться.

Последовательность действий по проверке лампы накаливания следующая:

В одну руку берут лампочку, касаясь резьбы (боковой контакт).
В другую руку берут индикаторную отвёртку и металлическим стержнем касаются центрального контакта лампы, а большим пальцем – торца отвёртки. Таким образом, цепь замыкается через отвёртку, лампу и тело человека. Весь тест занимает всего пару секунд.

Окончательный вывод формулы

Рассмотрим подробнее систему уравнений:

Возведем в квадрат первое уравнение и попарно перемножим их.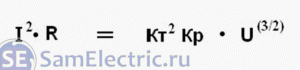

В левой части мы видим выражение для мощности, а так же памятуя о том, что произведение коэффициентов равно единице, окончательно перепишем:

Отсюда получим выражение для токового коэффициента:

И для резистивного коэффициента (они взаимообратны):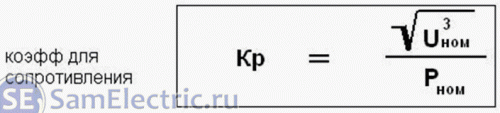где Рном и Uном – это номинальные мощность и напряжение, маркированные на цоколе или на колбе лампы.

Осталось подставить эти значения коэффициентов в “РАСЩЕПЛЕННУЮ” формулу Закона Ома, и мы получим окончательные выражения для тока и сопротивления.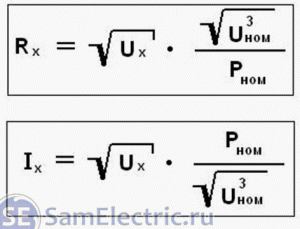

Домножая последнее соотношение на Ux, получим:

Чтобы не забивать себе голову этими квадратами, кубами и корнями, достаточно запомнить простую зависимость, которая вытекает из последнего соотношения . Возводя последнее соотношение в квадрат, мы получаем ясную и понятную формулу: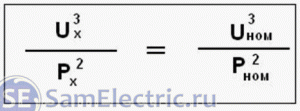

Для любой лампочки с вольфрамовой нитью накала отношение куба напряжения к квадрату мощности является величиной ПОСТОЯННОЙ.

Полученные соотношения показали прекрасное соответствие практическим результатам (измерениям) в широком диапазоне изменения параметров напряжения и для весьма различных типов ламп накаливания, начиная от комнатных, автомобильных и заканчивая лампочками для карманных фонариков…