Катушка индуктивности в цепи постоянного и переменного тока

§ 2.9. Закон Ома для электрической цепи переменного тока

Рассмотрим теперь более общий случай электрической цепи, в которой последовательно соединены проводник с активным сопротивлением R и малой индуктивностью, катушка с большой индуктивностью L и малым активным сопротивлением и конденсатор емкостью С (рис. 2.20).

Рис. 2.20

Чему равна амплитуда силы тока в такой цепи (колебательном контуре), если на ее концах поддерживается напряжение u(t) = U sin ωt?

Мы видели, что при включении по отдельности в цепь проводника с активным сопротивлением R, конденсатора емкостью С или катушки с индуктивностью L амплитуда силы тока определяется соответственно формулами (2.6.2), (2.7.3) и (2.8.4). Амплитуды же напряжений на резисторе, катушке индуктивности и конденсаторе связаны с амплитудой силы тока так:

В цепях постоянного тока напряжение на концах цепи равно сумме напряжений на отдельных последовательно соединенных участках цепи. Однако, если измерить результирующее напряжение на контуре и напряжения на отдельных элементах цепи переменного тока, окажется, что напряжение на контуре (действующее значение) не равно сумме напряжений на отдельных элементах.

Почему это так? Дело в том, что гармонические колебания напряжения на различных участках цепи сдвинуты по фазе друг относительно друга.

Действительно, квазистационарный ток в любой момент времени одинаков во всех участках цепи. Это значит, что одинаковы амплитуды и фазы токов, протекающих по участкам с емкостным, индуктивным и активным сопротивлением. Однако только на участке с активным сопротивлением колебания напряжения и силы тока совпадают по фазе. На конденсаторе колебания напряжения отстают по фазе от колебаний силы тока на π/2 (см. § 2.7), а на катушке индуктивности колебания напряжения опережают колебания силы тока на π/2 (см. § 2.8).

Векторная диаграмма электрической цепи

Для вывода закона Ома в случае электрической цепи переменного тока, изображенной на рисунке 2.20, нужно уметь складывать мгновенные колебания напряжений, сдвинутых по фазе друг относительно друга. Проще всего выполнять сложение нескольких гармонических колебаний с помощью векторных диаграмм, о которых было рассказано в § 1.11. Векторная диаграмма электрических колебаний в цепи позволит нам определить амплитуду силы тока в зависимости от амплитуды напряжения и сдвиг фаз между силой тока и напряжением.

Так как сила тока одинакова во всех участках цепи, то построение векторной диаграммы удобно начать с вектора силы тока _m. Этот вектор изобразим в виде вертикальной стрелки (рис. 2.21). Напряжение на резисторе совпадает по фазе с силой тока. Поэтому вектор _mR должен совпадать по направлению с вектором _m. Его модуль равен U_mR = I_mR.

Рис. 2.21

Колебания напряжения на катушке индуктивности опережают колебания силы тока на π/2 и соответствующий вектор и _mL должен быть повернут относительно вектора _m на π/2. Его модуль равен U_mL = IωL. Если считать, что положительному сдвигу фаз соответствует поворот вектора против часовой стрелки, то вектор _mL следует повернуть налево на π/2. (Можно было бы, конечно, поступить и наоборот.)

Вектор напряжения на конденсаторе _mC отстает по фазе от вектора _m на π/2 и поэтому повернут на этот угол относительно вектора _m направо. Его модуль равен .

Для нахождения вектора суммарного напряжения _m нужно сложить три вектора: _mR, _mL и _mC. Вначале удобнее сложить два вектора _mL и _mC (рис. 2.22).

Рис. 2.22

Модуль этой суммы равен , если . Именно такой случай изображен на рисунке. После этого, сложив вектор _mL + _mC с вектором _mR, получим вектор _m, характеризующий колебания напряжения в сети.

По теореме Пифагора (из треугольника АОВ):

или

Из равенства (2.9.2) можно найти амплитуду силы тока в цепи:

Это и есть закон Ома для электрической цепи переменного тока, изображенной на рисунке 2.20.

Благодаря сдвигу фаз между напряжениями на различных участках цепи полное сопротивление Z цепи (см. рис. 2.20) выражается так:

От амплитуд силы тока и напряжения можно перейти к действующим значениям этих величин. Они связаны друг с другом точно так же, как и амплитуды в формуле (2.9.3):

Мгновенное значение силы тока меняется со временем гармонически:

где φ_c, — разность фаз между силой тока и напряжением в сети. Она зависит от частоты со и параметров цепи R, L, С.

Сдвиг фаз между током и напряжением

Сдвиг фаз φ_c, между колебаниями силы тока и напряжения равен по модулю углу φ между векторами _m и _m (см. рис. 2.22). Как следует из этого рисунка,

Согласно рисунку 2.22, сила тока отстает от напряжения по фазе при условии . Поэтому сдвиг фаз φ_c = -φ и

В частных случаях цепей с активным, емкостным и индуктивным сопротивлениями из этой формулы получаются правильные значения сдвига фаз.

От чего зависит сопротивление конденсаторов цепей переменного тока

Показатели его, зависят не только от емкостных характеристик последнего, но и от частотной характеристики электротока, протекающего по цепи. Когда речь идет о сопротивлении резистора, то говорится о параметрах самого резистора, например, материале, форме, но полностью отсутствует взаимосвязь сопротивления его и показателей частоты электричества цепи (речь идет об идеальном резисторе, паразитные параметры которому не характерны). Когда речь идет об устройстве накопления энергии и заряда электрического поля — все иначе. Конденсатор одной и той же емкости при разных частотах тока обладает неодинаковым уровнем сопротивления. Амплитуда протекающего через него электричества при постоянной амплитуде напряжения обладает разной величиной.

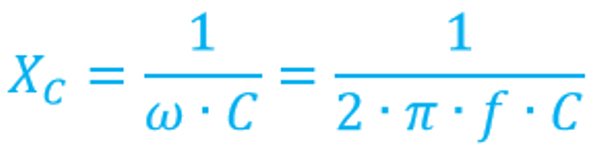
Вычисление Xc

Рассматривая эту формулу сопротивления конденсатора в цепи переменного тока, к каким выводам можно прийти? При повышении частотных показателей сигнала, электросопротивляемость конденсатора снижается.

При повышении емкостных характеристик устройства для накопления заряда и энергии электрического поля Xc переменного электричества, проходящего сквозь него, будет стремиться вниз.

Советуем изучить — Как устроены мощные промышленные ветрогенераторы

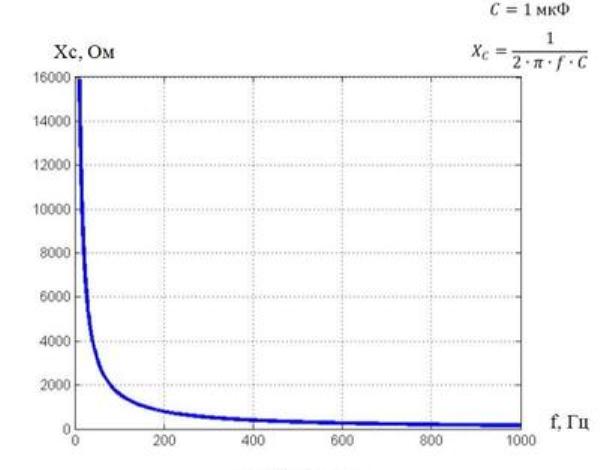
График, отображающий эту величину конденсатора при непостоянном токе цепи, имеет форму гиперболы

Момент приближения значений частоты к нулевым отметкам на оси (когда переменный электроток становится похож своими параметрами на постоянный), сопровождается возрастанием Xc конденсатора до беспредельных величин. Это действительно так: известно, что конденсатор сети постоянного тока является фактически разрывом цепи. Реальная электросопротивляемость, естественно, не бесконечна, ее ограничивает уровень конденсаторной утечки. Но величины его остаются на высоком уровне, который невозможно не учитывать.

При возрастании цифр частоты до уровня бесконечных значений, емкостное сопротивление электроконденсатора стремится к нулевым отметкам. Такое характеризует идеальные модели. В реальных условиях конденсатор имеет неприятные характеристики (такие как индуктивность и сопротивления утечек), поэтому снижение емкостного сопротивления происходит до определенных значений, после которых оно возрастает.

Обратите внимание! При подключении конденсатора к цепочке электричества с переменными параметрами, его мощность не тратится, потому что фазовые характеристики напряжения и силы тока сдвинуты на 90° в отношении друг друга. В одну четверть периода происходит зарядка электроконденсатора (энергия запасается в его электрополе), в следующее время происходит его разрядка, энергия поступает обратно в цепочку. Его электросопротивляемость является безваттной, реактивной

Его электросопротивляемость является безваттной, реактивной.

https://youtube.com/watch?v=DkbWbygA-Y4

Виды катушек

По функциональности различают контурные катушки, находящие применение в радиофизике, катушки связи, используемые в трансформаторах, и вариометры, то есть катушки, показатели которых можно варьировать изменением взаимного расположения катушек.

Также существует такой вид катушек, как дроссели. Внутри этого класса также есть деление на обычные и сдвоенные. Они имеют высокое сопротивление переменному току и очень низкое — постоянному, благодаря чему могут служить хорошим фильтром, пропускающим постоянный ток и задерживающим переменный. Сдвоенные дроссели отличаются большей эффективностью при больших токах и частотах по сравнению с обычными.

Немного больше про индуктивность

Мы уже разобрали это понятие, и теперь осталось поговорить о нём немного подробнее. Зачем? Нам ведь предстоит расчет индуктивности катушек, а значит, необходимо понимать, что это такое и зачем нам её рассчитывать.

Катушка индуктивности предназначена для создания магнитного поля, а значит, имеет параметры, которые описывают его силу. Таким параметром является магнитный поток. Но разные катушки имеют разные потери при прохождении через них тока и, соответственно, разный КПД. В зависимости от диаметра проводов и количества витков катушка может давать разное по величине магнитное поле. Значит, необходимо ввести такую величину, которая бы отражала зависимость между величиной магнитного потока и силой тока, пропускаемой через катушку. Таким параметром и является индуктивность.

Конструкция катушки

Катушки индуктивности имеют множество разновидностей по конструктивным особенностям. В основе любой конструкции лежит от одного и более витков изолированного провода.

Различают следующие конструкции по типу обмоток:

Соленоидальная – длина намотки многократно превышает диаметр;
Тороидальная – когда соленоид свернут в форме тора.
Многослойная – разновидность соленоида при наличии нескольких рядов обмоток;
Секционированная – обмотки состоят из нескольких частей – секций;
С намоткой «Универсал».

Вам это будет интересно Измерение потребляемой мощности Две последних разновидности используются при необходимости снижения собственной паразитной емкости.

Секционированная катушка с обмоткой «универсал»

Важно! Все перечисленные разновидности могут быть выполнены с сердечником из ферромагнитного материала для увеличения индуктивности при сохранении габаритов. Регулировка (изменение) индуктивности производится путем:

Регулировка (изменение) индуктивности производится путем:

Сдвига части витков в однослойных катушках;
Изменением положения ферромагнитного сердечника;
Переключением части витков;
Изменение взаимного расположения обмоток, соединенных последовательно (вариометры).

Что влияет на индуктивность?

От каких факторов зависит индуктивность катушки? Давайте проведем несколько опытов. Я намотал катушку с немагнитным сердечником. Ее индуктивность настолько мала, что LC – метр мне показывает ноль.

Имеется ферритовый сердечник

Начинаю вводить катушку в сердечник на самый край

LC-метр показывает 21 микрогенри.

Ввожу катушку на середину феррита

35 микрогенри. Уже лучше.

Продолжаю вводить катушку на правый край феррита

20 микрогенри. Делаем вывод, самая большая индуктивность на цилиндрическом феррите возникает в его середине. Поэтому, если будете мотать на цилиндрике, старайтесь мотать в середине феррита. Это свойство используется для плавного изменения индуктивности в переменных катушках индуктивности:

где

1 – это каркас катушки

2 – это витки катушки

3 – сердечник, у которого сверху пазик под маленькую отвертку. Вкручивая или выкручивая сердечник, мы тем самым изменяем индуктивность катушки.

Экспериментируем дальше. Давайте попробуем сжимать и разжимать витки катушки. Для начала ставим ее в середину и начинаем сжимать витки

Индуктивность стала почти 50 микрогенри!

А давайте-ка попробуем расправим витки по всему ферриту

13 микрогенри. Делаем вывод: для максимальной индуктивности мотать катушку надо “виток к витку”.

Убавим витки катушки в два раза. Было 24 витка, стало 12.

Совсем маленькая индуктивность. Убавил количество витков в 2 раза, индуктивность уменьшилась в 10 раз. Вывод: чем меньше количество витков – тем меньше индуктивность и наоборот. Индуктивность меняется не прямолинейно виткам.

Давайте поэкспериментируем с ферритовым кольцом.

Замеряем индуктивность

15 микрогенри

Отдалим витки катушки друг от друга

Замеряем снова

Хм, также 15 микрогенри. Делаем вывод: расстояние от витка до витка не играет никакой роли в катушке индуктивности тороидального исполнения.

Мотнем побольше витков. Было 3 витка, стало 9.

Замеряем

Офигеть! Увеличил количество витков в 3 раза, а индуктивность увеличилась в 12 раз! Вывод: индуктивность меняется не прямолинейно виткам.

Если верить формулам для расчета индуктивностей, индуктивность зависит от “витков в квадрате”. Эти формулы я здесь выкладывать не буду, потому как не вижу надобности. Скажу только, что индуктивность зависит еще от таких параметров, как сердечник (из какого материала он сделан), площадь поперечного сечения сердечника, длина катушки.

Влияние напряжения и тока на потери мощности в дросселе

Как известно электрическая мощность на участке цепи определяется произведением мгновенных значений напряжения u и электрического тока i на этом участке

где R – сопротивление участка цепи.

Однако на практике неудобно пользоваться параметрами мгновенных значений, поэтому чаще всего оперируют величинами действующих значений напряжения U и тока I или средними значениями напряжения Ucp и тока Icp. Действующее значение характеризует тепловое действие переменного тока и напряжения, а среднее значение является среднеарифметическим значением всех амплитудных значений переменного напряжения за некоторый промежуток времени.

В радиоэлектронных приборах и устройствах используются различные типы переменных напряжений и токов, которые, кроме значений напряжений токов, характеризуются безразмерными параметрами: коэффициентом формы kф и коэффициентом амплитуды kа. Коэффициент амплитуды, как относятся между собой значения действующих значений к средним значениям, а коэффициент амплитуды – отношение амплитудного значения к действующему значению

Данные параметры характеризует форму переменного напряжения и тока. Рассмотрим некоторые типы форм напряжения.

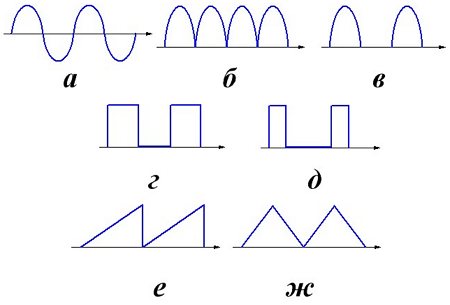
Некоторые формы напряжения и тока.

На рисунке изображено синусоидальное напряжение а, после двухполупериодного выпрямителя б, после однополупериодного выпрямителя в, прямоугольная форма (меандр, коэффициент заполнения D = 0,5) г, последовательность импульсов (коэффициент заполнения D ≠ 0,5) д, пилообразная форма е, треугольная форма ж. Для данных форм напряжения коэффициенты формы и амплитуды будут иметь значение

где D – коэффициент заполнения, равный отношению длительности импульса к его периоду,

ti – длительность импульса,

T – период следования импульсов,

f – частота следования импульсов.

Как видно из данных выражений, по известной форме переменного напряжения или тока достаточно просто определить активную мощность потребляемую нагрузкой, кроме того в случае прямоугольной формы напряжения изменяя длительность импульса можно регулировать действующее напряжение и электрический ток. Теперь разберёмся с сопротивлением дросселя и мощностью потерь в сердечнике.

Проверка питающего напряжения

Для проверки питающего напряжения катушки зажигания нам понадобится отключить топливный насос. Это нужно для того, чтобы двигатель не запускался во время проверки. Для этого находим и отключаем предохранитель бензонасоса.

Далее, отключаем питающий разъем с катушки зажигания. Берем канцелярскую скрепку, делаем из нее два проводника и вставляем в фишку питающего разъема. Подключаем мультиметр, лучше использовать зажимы типа «крокодил». Мультиметр в режиме постоянное напряжение (DC).

Теперь просто включите зажигание. Мультиметр должен показывать 0 вольт. Далее пытаемся завести двигатель, он не запустится, т. к. бензонасос отключен. В это время на катушки зажигания будет приходить пульсирующее напряжение 0-12 В. Это должно отображаться в показаниях мультиметра.

Если напряжение на разъем не приходит, нужно проверить проводку и разъемы на предмет повреждений и коррозии. После всех измерений подключите обратно предохранитель топливного насоса.

После того, как вы найдете неисправную катушку зажигания, просто замените ее на новую. Никаких дополнительных действий не требуется.

Предыдущая запись Электронная педаль газа Следующая запись Combiloader 2.1.8 — программа для прошивки ВАЗ, ГАЗ, УАЗ Лайк 5Добавить комментарий Отменить ответ

Комментарий

Вам также может понравиться Ошибка P0322 — датчик оборотов двигателя, слабый сигнал Расшифровка P0322 Код P0322 говорит о том, что блок02.5k. Ошибка P0120 — Датчик положения дроссельной заслонки / педали, неисправность электрической цепи Расшифровка P0120 Ошибка P0120 значит, что есть неисправность03k. Ошибка P0089 — неисправность регулятора давления топлива 1 Код ошибки P0089 определяется как «Производительность02.1k.текстареа>текстареа>

Снятие модуля

Чтобы снять неисправный блок, потребуется:

Отключить аккумулятор от бортовой сети и снять корпус воздушного фильтра.
Отсоединить высоковольтные кабели и жгут электропроводки.
Отвернуть 3 гайки, которые удерживают узел на монтажной площадке.

Прочитайте, может пригодится: Ссылки на схемы электрооборудования.

Особенности замены

Установить катушку можно без применения специального инструмента. Система зажигания инжекторных двигателей не требует корректировки работы. Положение дроссельной заслонки настраивают в режиме холостого хода и максимального газа. При сбоях в работе необходимо проверить и выставить по меткам на шкиве привода внешних агрегатов датчик положения коленчатого вала.

Индуктивное сопротивление катушки

Так как самоиндукция препятствует всякому резкому изменению силы тока в цепи, то, следовательно, она представляет собой для переменного тока особого рода сопротивление, называемое индуктивным сопротивлением. Чисто индуктивное сопротивление отличается от обычного (омического) сопротивления тем, что при прохождении через него переменного тока в нем не происходит потери мощности.

Под чисто индуктивным сопротивлением мы понимаем сопротивление, оказываемое переменному току катушкой, проводник которой не обладает вовсе омическим сопротивлением. В действительности же всякая катушка обладает некоторым омическим сопротивлением. Но если это сопротивление невелико по сравнению с индуктивным сопро¬тивлением, то им можно пренебречь.

При этом наблюдается следующее явление: в течение одной четверти периода, когда ток возрастает, магнитное поле потребляет энергию из цепи, а в течение следующей четверти периода, когда ток убывает, возвращает ее в цепь. Следовательно, в среднем за период в индуктивном сопротивлении мощность не затрачивается. Поэтому индуктивное сопротивление называется реактивным (прежде его неправильно называли безваттным).

Индуктивное сопротивление одной и той же катушки будет различным для токов различных частот. Чем выше частота переменного тока, тем большую роль играет индуктивность и тем больше будет индуктивное сопротивление данной катушки. Наоборот, чем ниже частота тока, тем индуктивное сопротивление катушки меньше. При частоте, равной нулю (установившийся постоянный ток), индуктивное сопротивление тоже равно нулю.

Рисунок 1. Зависимость индуктивного сопротивления катушки от частоты переменного тока. Реактивное сопротивление катушки возрастает с увеличением часторы тока.

Индуктивное сопротивление обозначается буквой XL и измеряется в омах.

Подсчет индуктивного сопротивления катушки для переменного тока данной частоты производится по формуле

XL=2π• f •L

где XL — индуктивное сопротивление в ом; f—частота переменного тока в гц; L — индуктивность катушки в гн

Как известно, величину 2π• f называют круговой частотой и обозначают буквой ω (омега). Поэтому приведенная выше формула может быть представлена так:

Отсюда следует, что для постоянного тока (ω = 0) индуктивное сопротивление равно нулю. Поэтому, когда, нужно пропустить по какой-либо цепи постоянный ток, задержав в то же время переменный, то в цепь включают последовательно катушку индуктивности.

Для преграждения пути токам низких звуковых частот ставят катушки с железным сердечником, так называемые дроссели низкой частоты, а для более высоких радиочастот — без железного сердечника, которые носят название дросселей высокой частоты.

Источник

Для чего она нужна и где используется

Подобные элементы находят множество применений, но наиболее часто они используются в качестве:

Элементов индуктивности в слаботочных электрических цепях;
Реакторов в силовой электронике, в качестве элементов компенсации реактивного характера нагрузки;
Дросселей для сглаживания пульсаций выпрямленного или переменного тока;
Электромагнитов в качестве источников магнитного поля в электромагнитных реле или органах управления различных устройств;
Индукторов в установках индукционного нагрева;
Накопителя энергии в источниках преобразования напряжения;
Датчиков магнитных полей (магнитные головки в накопителях на жестких магнитных дисках);
Линий задержки сигнала;
Антенн для приема и передачи электромагнитных волн.

Индуктивная антенна

https://youtube.com/watch?v=JCIeCusWG9w

https://youtube.com/watch?v=i_88KLuFwqs

Полное сопротивление цепи переменного тока

В предыдущих статьях мы узнали, что всякое сопротивление, поглощающее энергию, называется активным, а сопротивление, не поглощающее энергии, безваттным или реактивным. Кроме того, мы установили, что реактивные сопротивления делятся на два вида — индуктивные и емкостные.

Однако существуют цепи, где сопротивление не является чисто активным или чисто реактивным. То есть цепи, где вместе с активным сопротивлением включены в цепь, как емкости, так и индуктивности.

Введем понятие полного сопротивления цепи переменному току — Z, которое соответствует векторной сумме всех сопротивлений цепи (активных, емкостных и индуктивных). Понятие полного сопротивления цепи нам необходимо для более полного понимания закона Ома для переменного тока

На рисунке 1 представлены варианты электрических цепей и их классификация в зависимости от того какие элементы (активные или реактивные) включены в цепь.

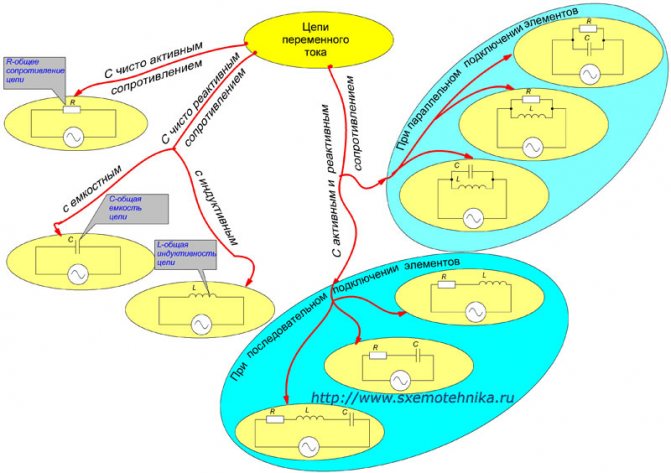
Рисунок 1. Классификация цепей переменного тока.

Полное сопротивление цепи с чисто активными элементами соответствует сумме активных сопротивлений цепи и рассматривалось нами ранее. О чисто емкостном и индуктивном сопротивлении цепи мы тоже с вами говорили, и оно зависит соответственно от общей емкости и индуктивности цепи.

Рассмотрим более сложные варианты цепи, где последовательно с активным сопротивлением в цепь включено индуктивное и реактивное сопротивление.

Принцип действия

Принцип действия катушки индуктивности заключается в создании и взаимодействии магнитного потока витками обмотки.

Если взять в упрощенном случае единичный виток, то при прохождении через него электрического тока, создается магнитный поток, движущийся вдоль поверхности контура, пропорциональный величине тока и значению индуктивности:

Ф=L·I, где

Ф – магнитный поток;

L – индуктивность;

I – сила тока.

Важно! Катушки в подавляющем большинстве случаев представляют собой многовитковую конструкцию, поэтому образуют сложную поверхность и расчеты параметров производятся в упрощенном виде. Магнитный поток соленоидальной катушки

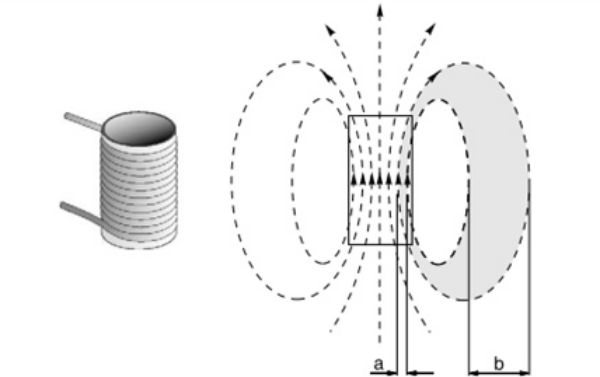
Магнитный поток соленоидальной катушки

Образование магнитного потока каждым из витков и взаимодействие его с остальными (магнитная индукция) приводит к возникновению ЭДС самоиндукции, которая заключается в том, что, при изменении величины протекающего тока в катушке, образуется ЭДС и, соответственно, ток, направленный, чтобы противодействовать изменениям.

В случае переменного тока это приводит к тому, что фаза тока отстает от фазы напряжения на 90°. Данное свойство используется в компенсаторах реактивного сопротивления (реакторах), дросселях, линиях задержки.

Важно! Величина ЭДС самоиндукции прямо пропорциональна скорости изменения тока. Это позволяет разрабатывать источники высоковольтного напряжения

Автомобильная катушка зажигания состоит из двух обмоток – низковольтной и высоковольтной. При размыкании питания в низковольтной обмотке в ней формируется импульс ЭДС самоиндукции, который в высоковольтной обмотке достигает десятков тысяч вольт.

Автомобильная катушка зажигания

Сопротивление катушки индуктивности включает две составляющих:

Индуктивное сопротивление;
Сопротивление потерь.

Вам это будет интересно Особенности проводимости меди

Индуктивное сопротивление (реактивное сопротивление, импеданс) зависит от частоты протекающего тока:

XL = 2·π·f·L, где

π – 3.14;

f – частота;

L – индуктивность.

Сопротивление потерь включает в себя:

Потери в проводах (активное сопротивление катушки);
Потери на вихревые токи;
Потери в сердечнике;
Потери в диэлектрике.

Важно! Некоторые потери вносит также распределенная емкость, которую снижают путем использования особой конфигурации обмоток, разделения ее на секции. Основную долю потерь вносит активное сопротивление

Основную долю потерь вносит активное сопротивление.

Профессиональное тестирование

Понадобится оборудование профессионального класса. Оптимальным решением станет отведение отдельного стенда под проверку катушек. Так можно будет задавать различные скоростные режимы валикам, проводя имитации разных типов работ.

При взаимодействии нужно следить за тем, чтобы постоянно поддерживалась искра вне зависимости от рабочего режима. Перед проведением проверки нужно убедиться в правильном подсоединении данного питания, в противном случае можно получить недостоверные данные, что помешает определению неполадок.

https://youtube.com/watch?v=QsCOkB6Hg00

Для чего нужны и какие бывают

В зависимости от того, где применяется катушка индуктивности и её функциональных особенностей, она может называться по-разному: дроссели, соленоиды и прочее. Давайте рассмотрим, какие бывают катушки индуктивности и их сферу применения.

Дроссели. Обычно так называются устройства для ограничения тока, область применения:

В пускорегулирующей аппаратуре для розжига и питания газоразрядных ламп.
Для фильтрации помех. В блоках питания — фильтр электромагнитных помех со сдвоенным дросселем на входе компьютерного БП, изображен на фото ниже. Также используется в акустической аппаратуре и прочем.
Для фильтрации определенных частот или полосы частот, например, в акустических системах (для разделения частот по соответствующим динамикам).
Основа в импульсных преобразователях — накопитель энергии.

Токоограничивающие реакторы — используются для ограничения токов короткого замыкания на ЛЭП.

Примечание: у дросселей и реакторов должно быть низкое активное сопротивление для уменьшения их нагрева и потерь.

Контурные катушки индуктивности. Используются в паре с конденсатором в колебательном контуре. Резонансная частота подбирается под частоту приема или передачи в радиосвязи. У них должна быть высокая добротность.

Вариометры. Как было сказано — это настраиваемые или переменные катушки индуктивности. Чаще всего используются в тех же колебательных контурах для точной настройки частоты резонанса.

Соленоид — так называется катушка, длина которой значительно больше диаметра. Таким образом внутри соленоида образуется равномерное магнитное поле. Чаще всего соленоиды используются для совершения механической работы — поступательного движения. Такие изделия называют еще электромагнитами.

Рассмотрим, где используются соленоиды.

Это может быть активатор замка в автомобиле, шток которого втягивается после подачи на соленоид напряжения, и звонок, и различные исполнительные электромеханические устройства типа клапанов, грузоподъёмные магниты на металлургических производствах.

В реле, контакторах и пускателях соленоид также выполняет функцию электромагнита для привода силовых контактов. Но в этом случае его чаще называют просто катушка или обмотка реле (пускателя, контактора соответственно), как выглядит, на примере малогабаритного реле вы видите ниже.

Рамочные и кольцевые антенны. Их назначение — передача радиосигнала. Используются в иммобилайзерах автомобилей, металлодетекторах и для беспроводной связи.

Индукционные нагреватели, тогда она называется индуктором, вместо сердечника помещают нагреваемое тело (обычно металл).

Фазор

Благодаря фазовым векторам сложный и меняющийся во времени сигнал можно представить в виде комплексного числа (не зависит от времени) и сложного сигнала (зависит от времени). Фазоры делятся на основе А (амплитуды), v (частоты) и θ (фазы). Это приносит большую пользу, ведь частотный коэффициент часто выступает общим для всех компонентов линейной комбинации синусоид. В подобных ситуациях факторы исключают факультативную характеристику и основываются лишь на A и θ.

Советуем изучить Источники питания 24 и 12 Вольт

К примеру, можно представить A⋅cos (2πνt + θ) просто как комплексную постоянную Aeiθ. Из-за того, что фазовые векторы передаются величиной и углом, наглядно изображаются вектором в плоскости x-y.

Фазор можно рассматривать с позиции вектора, вращающегося вокруг начала координат. Косинусная функция – проекция вектора на ось. Амплитуда выступает модулем вектора. Постоянная фазы – угол, сформированный вектором и осью при t = 0