Микросхемы шифраторы
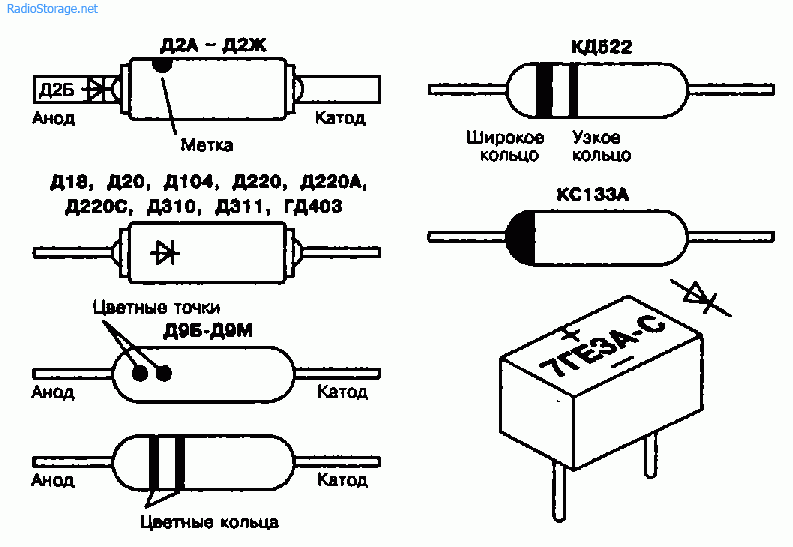
Микросхемы шифраторы применяются значительно реже, чем дешифраторы. Они имеют обозначение на схемах буквами CD, а в названии микросхем имеют суффикс ИВ. Как понятно из названия они выполняют функцию обратную микросхемам дешифраторов и обычно имеют от 4 до 16 (чаще всего 8) информационных входов, от 2 до 4 выходов (чаще всего 3) и несколько стробирующих (разрешающих) входов и выходов. Типичными представителями данных типов микросхем являются микросхемы К555ИВ1 и К555ИВ3 которые изображены ниже.
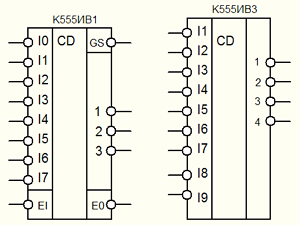
Микросхемы шифраторы: слева направо К555ИВ1, К555ИВ3.
Микросхема К555ИВ1 является шифратором и содержит 8 информационных входов и три выхода, а также вход разрешения EI, выход признака прихода любого входного сигнала GS и выход переноса ЕО, для объединения нескольких шифраторов. Работа данного шифратора разрешается только при низком логическом уровне на входе EI, а при высоком уровне на нём на всех выходах устанавливается уровень логической единицы. В случае отсутствия каких-либо сигналов на входах на выходе GS вырабатывается логическая единица, а на выходе ЕО логический нуль. Запишем таблицу истинности для данной микросхемы.
| Входы | Выходы | ||||||||||||
| EI | 1 | 2 | 3 | 4 | 5 | 6 | 7 | GS | 4 | 2 | 1 | EO | |
| 1 | X | X | X | X | X | X | X | X | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| X | X | X | X | X | X | X | 1 | ||||||
| X | X | X | X | X | X | 1 | 1 | 1 | |||||
| X | X | X | X | X | 1 | 1 | 1 | 1 | |||||
| X | X | X | X | 1 | 1 | 1 | 1 | 1 | 1 | ||||
| X | X | X | 1 | 1 | 1 | 1 | 1 | 1 | |||||
| X | X | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||
| X | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Таблица истинности шифратора К555ИВ1.
Наиболее часто шифраторы применяют для сокращения количества сигнальных линий, что очень удобно при передачи сигналов на большие расстояния, но при этом, входные сигналы не должны приходить одновременно на все входы. Наличие у шифратора дополнительных входных и выходных линий позволяет объединить их для увеличении разрядности шифратора, но только с помощью дополнительных логических элементов.
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.
Как происходит заражение
Главная цель злоумышленников заставить пользователя любым способом скачать файл с вирусом и запустить его. В этом вымогатели могут проявлять всю свою фантазию.
Зачастую они устраивают массовую рассылку писем в организации. В теме сообщения указывается «резюме», «исковое требование», «договор поставки», «акт сверки-взаиморасчётов», т. е. самые обычные письма, которые ежедневно проходят десятками в любой организации. Стоит ли говорить, что, например, сотрудник отдела кадров, зачастую не самый продвинутый пользователь, с большой вероятностью скачает прикрепленный файлик «резюме» и откроет его.
Другой способ распространения вируса — это запуск скачанной с интернета программы. Только вместо установки программы пользователь получает зашифрованные файлы. Забавно, вроде бы все на месте, но в таком виде они абсолютно бесполезны.
Схема — шифратор
Из сказанного можно сделать вывод, что схема шифратора 8 / 3 ( рис. 8.2) состоит из трех четырехвходовых дизъюнкторов.
Если в РТС используется ФИМ, ШИМ или КИМ, то обычно в схему шифратора добавляется блок преобразования АИМ. Этот блок устанавливается между коммутатором и передатчиком. В дешифраторе в этом случае используется блок обратного преобразования, включаемый между приемником и коммутатором Kz. Характерной особенностью многоканальных радиолиний с временным разделением каналов является передача сообщений в отдельные ( дискретные) моменты времени.
|
Выходные сигналы шифратора КРУ со счетно-импульсной модуляцией. |
В соответствии с сущностью рассматриваемого способа передачи команд может быть разработана функциональная и принципиальная схемы шифратора. В качестве примера на рис. 27 — 45 приведена схема шифратора двухканальной КРУ с импульсными поднесущими, разделение которых на приемной стороне производится в соответствии с принципом кодовой селекции. При этом предполагается, что выходные команды КУ1 и Куз представляют собой напряжения постоянного тока.
Ячейка памяти сигнализации ( ЯС); предназначена для фиксации изменения состояния объектов ТС, запуска схемы шифратора на КП и осуществления циркулярной передачи состояния объектов. Она управляется переключающимися блок-контактами объектов ТС, состоит из одного МГЭ, триода, диодов и сопротивлений и имеет три выхода.
Таким образом, шифратор Ш связан с автопереключателем А / 7, причем часть конструктивных элементов последнего входит в схему шифратора. ИГ, связанный с автопереключателем двойной связью: с одной стороны генег ратор подает в АП импульсы движения, е другой — переключатель останавливает пульс-генератор по получении комплекта импульсов.
Рассмотренные примеры многопроводных систем относятся к случаю малого числа управляемых объектов на каждом ИП, поэтому здесь имеется возможность применить упрощенные решения для схем шифраторов и дешифраторов. Различение импульсов на приемной стороне осуществляется, как правило, обычными реле, или бесконтактными переключающими элементами.
Этой системе логических выражений соответствует схема на рис. 3.19 а. На рис. 3.196 изображена схема шифратора на элементах ИЛИ-НЕ.
|
Стартстопные распределители. |
В простейших шифраторах подобного типа изменение полярности сигнала на их выходе производится с помощью контактных групп, которые могут переключаться вручную или же с помощью реле. На рис. 23 — 27 приведены схемы шифраторов полярности сигналов с одной ( рис. 23 — 27, а) и с двумя ( рис. 23 — 27, б) переключающими контактными группами.
|
Шифраторы полярности сигналов.| Дешифраторы полярности сигналов. |
В шифраторах числа импульсов со стартстопными распределителями могут использоваться самые разнообразные типы распределителей. На рис. 23 — 29 приведены схемы шифратора числа импульсов с электромагнитным шаговым распределителем, генератором импульсов и отсекающим реле. В этом шифраторе используется распределитель обратного хода, имеющий два ряда неподвижных контактных ламелей. Роль суммирующего устройства выполняет отсекающее реле Ра-В исходном положении шифратора щетки распределителя стоят на нулевых ламелях, а все реле и электромагнит ЭМ распределителя находятся в положении покоя.
Устройство ввода ( УВ) обеспечивает ручной ввод цифровой информации, знака числа, запятой и включение операций. В устройство ввода входят блок функционально-цифровой клавиа-туры и схема шифратора.
После пере ключения клавишного контакта на вход 3 схемы шифратора под ключается сигнал высокого уровня напряжения 1, который через диоды Д5, Д8 и Д11 поступает на выход шин 1 и 2, а также Подключает шину Ввод. Следовательно, при нажатии на кла вишу 3 на выходе шифратора образуются двоично-десятичный код ООП и управляющий сигнал для занесения кода цифры в регистр.
В соответствии с сущностью рассматриваемого способа передачи команд может быть разработана функциональная и принципиальная схемы шифратора. В качестве примера на рис. 27 — 45 приведена схема шифратора двухканальной КРУ с импульсными поднесущими, разделение которых на приемной стороне производится в соответствии с принципом кодовой селекции. При этом предполагается, что выходные команды КУ1 и Куз представляют собой напряжения постоянного тока.
Расшифровка шифра Вернама
Если у нас есть закодированное сообщение и ключ от него, то раскодировать его не составит труда. Мы просто пишем алгоритм, который применяет операцию XOR как бы в обратном порядке к каждому биту сообщения. Например:
- Если в ключе шифрования в каком-то бите стоит 1, то мы берём этот же бит в зашифрованном сообщении и меняем его. Если был 1, то меняем на 0. Если был 0, то меняем на 1.
- Если в ключе шифрования в каком-то бите стоит 0, то этот же бит в зашифрованном сообщении мы не меняем.
- Проходим так по каждому биту сообщения и получаем исходный текст.
Компьютер может совершать миллиарды таких операций в секунду. Главное — иметь на руках ключ для расшифровки.
2 основных типа алгоритмов асимметричного шифрования
1. Алгоритм асимметричного шифрования RSA
В 1977 году алгоритм изобрели трое ученых из Массачусетского технологического института Рон Ривест, Ади Шамир и Леонард Адлеман (Ron Rivest, Adi Shamir, and Leonard Adleman отсюда «RSA»). На сегодняшний день является наиболее используемым алгоритмом асимметричного шифрования. Его эффективность заключается в методе «первичной факторизации». По сути, выбираются два различных случайных простых числа заданного размера (например, 1024 бита каждое) и умножаются, чтобы создать еще одно гигантское число. Задача состоит в том, чтобы определить исходные простые числа из умноженного гигантского. Оказывается, эта головоломка практически невозможна для современных суперкомпьютеров, не говоря уже о людях.
В 2010 году группа добровольцев провела исследование, и им потребовалось более 1500 лет вычислительного времени (распределенного по сотням компьютеров), чтобы взломать 768-битный ключ RSA, что намного ниже стандартного 2048-битного, который используется сегодня.
Преимущество использования алгоритма шифрования RSA
Большим преимуществом RSA является его масштабируемость, ключи могут быть разной длины шифрования: 768-битный, 1024-битный, 2048-битный, 4096-битный и т. д.
RSA основан на простом математическом подходе, поэтому его реализация в инфраструктуре открытых ключей (PKI) становится легкой. Адаптивность и безопасность сделали RSA наиболее используемым алгоритмом асимметричного шифрования для различных приложений, включая сертификаты SSL / TLS, криптовалюты и шифрование электронной почты.
2. Алгоритм асимметричного шифрования ECC
В 1985 году два математика по имени Нил Коблиц и Виктор Миллер предложили использовать эллиптические кривые в криптографии. Спустя почти два десятилетия их идея воплотилась в реальность, алгоритм ECC (Elliptic Curve Cryptography) начали использовать в 2004-2005 годах.
В процессе шифрования ECC эллиптическая кривая представляет набор точек, которые удовлетворяют математическое уравнение (y 2 = x 3 + ax + b).
Как и RSA, ECC также работает по принципу необратимости. Проще говоря, в ECC число, символизирующее точку на кривой, умножается на другое число и дает другую точку на кривой. Теперь, чтобы взломать эту головоломку, вы должны выяснить новую точку на кривой. Математика ECC построена таким образом, что найти новую точку практически невозможно, даже если вы знаете исходную точку.
Преимущество использования алгоритма шифрования ECC
Не смотря на то, что по сравнению с RSA, в ECC используется более короткая длина ключа обеспечивает он большую безопасность (от современных методов взлома).
Еще одним преимуществом использования более коротких ключей в ECC является более высокая производительность. Короткие ключи требуют меньшей сетевой нагрузки и вычислительной мощности, и это отлично подходит для устройств с ограниченными возможностями хранения и обработки. Использование алгоритма ECC в сертификатах SSL/TLS значительно сокращает время, необходимое для шифрования и дешифрования, что помогает быстрее загружать веб-сайт. Алгоритм ECC используется для приложений шифрования, цифровых подписей, в псевдослучайных генераторах и т. д.
Однако проблема массового использования ECC заключается в том, что многие серверные программы и панели управления еще не добавили поддержку сертификатов ECC SSL/TLS. Мы надеемся, что это изменится в скором будущем, а пока что RSA будет продолжать оставаться наиболее используемым алгоритмом асимметричного шифрования.
Другие формы двоичного кода
Даосский багуа
Битовая строка — не единственный тип двоичного кода: фактически, двоичная система в целом — это любая система, которая допускает только два выбора, например, переключатель в электронной системе или простой тест на истинность или ложь.
Шрифт Брайля
Брайль — это тип двоичного кода, который широко используется слепыми для чтения и записи на ощупь, названный в честь его создателя Луи Брайля. Эта система состоит из сеток из шести точек в каждой, по три на столбец, в которых каждая точка имеет два состояния: поднято или не поднято. Различные комбинации выпуклых и плоских точек могут представлять все буквы, цифры и знаки препинания.
Багуа
В Багуа представлены диаграммы , используемые в фэн — шуй , даосской космологии и я Ching исследований. Ба гуа состоит из 8 триграмм; bā означает 8, а guà означает фигуру гадания. То же слово используется для 64 гуа (гексаграмм). Каждая фигура состоит из трех линий ( yáo ), которые либо прерваны ( инь ), либо не прерваны ( янь ). Отношения между триграммами представлены в двух формах: изначальном багуа «Раннее небо» или «Фукси» и проявленном багуа «Позднее небо» или «Король Вэнь» . (См. Также последовательность 64 гексаграмм короля Вэня ).
Ифа, Ильм аль-Рамл и геомантия
Система гадания Ифа / Ифе в африканских религиях, таких как йоруба , игбо , эве , состоит из сложной традиционной церемонии, производящей 256 оракулов, составленных из 16 символов с 256 = 16 x 16. Посвященный священник « бабалово », который запомнил оракулы, просили жертв у консультантов и возносили молитвы. Затем орехи гадания или пара цепочек используются для получения случайных двоичных чисел, которые рисуются песчаным материалом на фигурном деревянном подносе «Опун», представляющем совокупность судьбы.
Благодаря распространению исламской культуры Ифе / Ифа была ассимилирована как «Наука о песке» (ilm al-raml), которая затем распространилась дальше и стала «Наукой чтения знаков на земле» ( геомантия ) в Европе.
Считалось, что это еще один возможный путь, на котором была вдохновлена информатика, поскольку геомантия пришла в Европу на более раннем этапе (около 12 века, описанного Хью Санталла ), чем И Цзин (17 век, описанный Готфридом Вильгельмом Лейбницем ).
Пример работы
Если мы зашифруем так фразу «Привет, это журнал Код!», то можем получить что-то такое:
hi857ов9njg5jоlр6;p0ора
Штука в том, что одна и та же буква в шифровке не означает одинаковые буквы в исходном сообщении, потому что биты шифрования выбраны случайным образом. Поэтому при попытке расшифровки злоумышленник получит такие варианты:
Срочно подпишись на код
Верни деньги, а то вилы
мама, я сдал зачёт, ура
Ваш зам предатель и вор
Ваш зам ни при чём, вот
Также он может получить любые другие сочетания букв, цифр и пробелов в рамках тех 23 символов, которые у нас были в исходном сообщении. Может быть, это не текст вовсе, а набор цифр. Может быть, это текст на каком-то другом языке. Может быть, это не текст вовсе, а очень маленькая картинка. Все эти варианты можно получить из нашей зашифрованной строки, потому что злоумышленник не знает ключ.
Двоичная система (тоже нормальная)
Внутри компьютера работают транзисторы. У них нет знаков 0, 1, 2, 3… 9. Транзисторы могут быть только включёнными и выключенными — обозначим их и .
Мы можем научить компьютер шифровать наши числа этими транзисторами так же, как шестипалые люди шифровали наши числа буквами. Только у нас будет не 6 букв, а всего две: и . И выходит, что в каждом разряде будет стоять не число десяток в разной степени, не число шестёрок в разной степени, а число… двоек в разной степени. И так как у нас всего два знака, то получается, что мы можем обозначить либо наличие двойки в какой-то степени, либо отсутствие:
| 0 — 1 — 2 — 4 — |
8 — 9 — 10 — 11 — 12 — 13 — 14 — 15 — |
16 — 17 — 18 — 19 — 20 — 21 — 21 — 23 — 24 — 25 — 26 — 27 — 28 — 29 — 30 — 31 — |
32 — 33 — 34 — 35 — 36 — 37 — 38 — 39 — 40 — 41 — 42 — 43 — 44 — 45 — 46 — 47 — 48 — 49 — 50 — 51 — 52 — 53 — 54 — 55 — 56 — 57 — 58 — 59 — 60 — 61 — 62 — 63 — |
Если перед нами число , мы можем разложить его на разряды, как в предыдущих примерах:
= 1 × 28 = 256
= 0 × 27 = 0
= 1 × 26 = 64
= 0 × 25 = 0
= 0 × 24 = 0
= 1 × 23 = 8
= 1 × 22 = 4
= 0 × 21 = 0
= 0 × 2 = 0
256 + 0 + 64 + 0 + 0 + 8 + 4 + 0 + 0 = 332
Получается, что десятипалые люди могут записать это число с помощью цифр 332, а компьютер с транзисторами — последовательностью транзисторов .
Если теперь заменить включённые транзисторы на единицы, а выключенные на нули, получится запись 1 0100 1100. Это и есть наша двоичная запись того же самого числа.
Дешифратор
Дешифратор на 2 входа
Это комбинационные схемы с несколькими входами и выходами, преобразующие код, подаваемый на входы в сигнал на одном из выходов. На выходе дешифратора появляется логическая единица, на остальных — логические нули, когда на входных шинах устанавливается двоичный код определённого числа или символа, то есть дешифратор расшифровывает число в двоичном, троичном или k-ичном коде, представляя его логической единицей на определённом выходе. Число входов дешифратора равно количеству разрядов поступающих двоичных, троичных или k-ичных чисел. Число выходов равно полному количеству различных двоичных, троичных или k-ичных чисел этой разрядности.
Для n-разрядов на входе, на выходе 2n, 3n или kn. Чтобы вычислить, является ли поступившее на вход двоичное, троичное или k-ичное число известным ожидаемым, инвертируются пути в определённых разрядах этого числа. Затем выполняется конъюнкция всех разрядов преобразованного таким образом числа. Если результатом конъюнкции является логическая единица, значит на вход поступило известное ожидаемое число.
Функциональная схема дешифратора на 2 входа
Из логических элементов являющихся дешифраторами можно строить дешифраторы на большое число входов. Каскадное подключение таких схем позволит наращивать число дифференцируемых переменных.
Дешифратор со стробированием
Блокирование (Е=0) выходе на время ПП внутри схемы (выполняет разрешающую функцию для всех выходов).
Демультиплексоры не используются, вместо них используются дешифраторы со стробированием
Основные определения
В начале изучим основы, чтобы в дальнейшем всё было понятно. Здесь не будет ничего сложного, чтобы полностью разобраться в теме, надо знать всего два определения и иметь представление о том, как работать с числами в двоичной системе счисления. Итак, приступим.
Код (в информатике) – это взаимно однозначное отображение символов одного алфавита (цифр) с помощью другого, который удобен для хранения, отображения и передачи данных.
На первый взгляд понятие может показаться непонятным, однако, оно совсем простое. Так, например, буквы русского алфавита мы можем представить с помощью десятичных, двоичных или любых других чисел в различных системах исчисления. Также буквы или слова можно закодировать любыми знаками. Однако тут есть одно условие – должны существовать правила, чтобы переводить значения назад. Исходя из этого положения возникает другое:
Кодирование (в информатике) – это процесс преобразования информации в код.
Для отображения текста разработчиками были придуманы так называемые кодировки – таблицы, где символам одного алфавита сопоставляются определенные числовые или текстовые значения. На данный момент относительно широкую популярность имеют две из них – ASCII и Unicode (Юникод). Ниже предложена информация, для ознакомления.
Примеры
Варианты классификации
Двоичные коды — это определения, согласно которым определенное количество битов связано, чтобы иметь возможность представлять определенное более высокое значение (чем просто двойная информация «да-нет»). Многочисленные варианты двоичных кодов можно классифицировать по разным критериям
Форма существования элементов двоичного кода (с примерами):
-
- видимые знаки (дымовые / световые знаки, QR-код )
- слышимые шумы / тоны (барабан)
- тактильные символы ( шрифт Брайля )
- Механически медиа — носители анализа ( перфокарты с отверстиями, контактный ролик в музыкальных коробках для музыки)
- электрические / электронные носители ( данные в компьютере или на электронных носителях данных, таких как жесткие диски или проводная передача данных ; радиотехнология ( WLAN ))
В связи с этим: Тип обработки кода: вручную без инструментов, механически, электронно.
Тип более важной информации: коды для чисел с фиксированной запятой, чисел с плавающей запятой, буквенно-цифровых символов.
Количество битов, объединенных в коде для формирования более важной информации: BCD-код = 4 (для чисел от 0 до 9), Hex-код = 4 (для значений от 0 до F, численно соответствует от 0 до 15), ASCII = 7, EBCDIC = 8-й
Фиксированная или переменная структура кода: фиксированная для большинства кодов символов, переменная, например. Б
Фотографии в формате JPG или машинный код
Использование контрольных битов в коде: нет, да (например, с кодом Грея )
Примеры кода
Двоичный код: значение / значение установленных битов в зависимости от кода
- Двойной код
Двойной код — это самый старый и наиболее часто используемый двоичный код, который может отображать целые числа в двойной системе . Он был описан еще в начале 18 века. Например, используя двойной код, вы можете использовать десять пальцев обеих рук для представления любого целого десятичного числа от 0 до 1023 ( ). Код определяет, сколько битов используется для представления чисел; общие примеры: 1 байт (= 8 бит), 2, 4 или 8 байтов.
210-1{\ displaystyle \ textstyle 2 ^ {10} -1}
- BCD код
В коде BCD цифры от 0 до 9 кодируются в четырех битах. Могут возникнуть числа от 0000 до 1001. Код BCD также известен как код 8-4-2-1.
- Код EBCDIC
Код EBCDIC, разработанный IBM, представляет собой 8-битную кодировку символов, основанную на более старом коде BCD и с индексом i. Кодируются прописные и строчные буквы, специальные символы и цифры от 0 до 9. EBCDIC используется почти исключительно на мэйнфреймах .
- Код ASCII
Американский стандартный код для обмена информации кодирует все символы , включая специальные английские символы в семи битах. С помощью кода ASCII можно закодировать до 128 ( ) различных символов. Во внутренней компьютерной обработке, ориентированной на блок хранения байтов, неиспользованному биту обычно присваивается «0».
27-е{\ displaystyle \ textstyle 2 ^ {7}}
- Машинный код
Код, который может выполняться непосредственно процессорами компьютера , определяется в наборе инструкций отдельных типов процессоров и всегда содержит код операции и, при необходимости, другую информацию, необходимую для выполнения инструкции, такую как адреса, литералы и т. Д. В точно определенном структура, например B. Код операции 8 бит, адресная информация 16 байтов, информация регистра 4 бита.
- Лишний код
Избыточный код также может быть использован для преобразования подписанных чисел в двоичный код. В основном смещен диапазон значений.
- Украденный код
Код Стибица — это дополнительный код BCD, иногда его также называют кодом лишних 3. Он также позволяет кодировать десятичные числа от 0 до 9.
- Код Айкен
Код Aiken также является дополнительным кодом BCD. Всем десятичным разрядам присваивается 4 бита. Он отличается от кода BCD только взвешиванием отдельных битов.
- Код 1 из N
Код 1 из n , также известный как код 1 из 10, кодирует десятичное число в n битах, из которых только один бит может быть 1 за раз. Контрольная сумма закодированного числа всегда дает 1. Однако такое кодирование не очень эффективно, поскольку теоретически с помощью n битов можно закодировать до различных чисел. Примером использования этого кода является перфокарта , где позиции отверстий от 0 до 9 использовались альтернативно для чисто числовых данных.
2п{\ Displaystyle \ textstyle 2 ^ {п}}
- Код Грея
Код Грея — это непрерывный или одноэтапный код. Его особенность в том, что соседние значения отличаются только на один бит. Преимущество в том, что небольшие неточности при считывании не приводят напрямую к неверной информации.
Что такое электронная подпись
Электронная подпись — это технология, которая помогает подтвердить подлинность электронного документа: договора, справки, выписки или чего-то ещё.
Если упрощённо, работает так:
Есть некий документ, подписанный ЭП
С помощью специальной программы можно проверить подлинность этой подписи и документа
Если программа говорит, что всё окей, то мы можем быть уверены: документ подписал именно тот, кто в нём указан; и с момента подписания в документе ничего не изменилось.
Или программа может сказать, что подпись не совпала. Это значит, что либо документ подписал другой человек, либо после подписания кто-то изменил этот документ (например, дописал ноль в стоимость контракта). Так мы поймём, что этому документу нельзя доверять.
С технической точки зрения ЭП — небольшой файлик, который прилагается к искомому документу. Файлик пересылается вместе с основным документом, его можно передавать по открытым каналам связи, в нём нет ничего секретного.
Электронная подпись нужна, чтобы защищать договоры, выдавать официальные справки, заключать сделки и участвовать в торгах по госзакупкам.
Как защититься от шифровальщиков
- Сохраняйте резервные копии ваших данных на внешний накопитель.
- Используйте антивирусные средства и не забывайте обновлять антивирусные базы. Как бы просто это не звучало, но это действительно может избавить вас от лишних проблем.
Ограничьте запуск некоторых потенциально опасных типов файлов. К примеру, с расширениями .js, .cmd, .bat, .vba, .ps1. Для этого нужно выполнить команду — gpedit.msc, далее перейти в раздел Конфигурация компьютера — Конфигурация Windows — Параметры безопасности — Политики управления приложениями — AppLocker — Правила сценариев, и с помощью мастера задать новое правило на запрет запуска всех сценариев для всех пользователей, например, на системном диске. Даже это простое действие может не раз спасти вас от неприятностей.
Будьте внимательны! Расскажите о вирусах шифровальщиках своим знакомым, чтобы они также не попадались на уловки мошенников. Все мы знаем, что предупрежден, значит вооружен!
Более подробную информацию о защите от шифровальщиков можно найти здесь.
В итоге, мы имеем серьезную угрозу для любого пользователя и довольно печальную статистику по расшифровке. Вирусы шифровальщики — это энигма нашего времени. Посмотрим, найдет ли кто-нибудь способ оставить мошенников без заработка.
Минусы шифра Вернама
Если бы у этого шифра не было минусов, все бы пользовались только им, но сейчас этот шифр используется редко. Всё дело в том, что им очень неудобно пользоваться, чтобы выполнить все условия.
Чтобы этот шифр нельзя было взломать, нужно, чтобы секретный ключ был у обеих сторон и при этом его нельзя было перехватить. Но если так можно передать секретный ключ, то вместо него можно передать и само сообщение.
Даже если удастся заранее передать набор ключей каждой стороне для будущих шифровок, их нужно держать в полной физической безопасности, чтобы нельзя было их украсть, подсмотреть, потерять или перепутать.
Именно из-за таких требований к безопасности ключа этот шифр сейчас используется очень редко.
Принцип работы дешифратора
Дешифраторы используются для преобразования двоичных чисел в десятичные числа и находят применение в печатающих устройствах. В таких устройствах двоичное число, поступая на вход дешифратора, вызывает появление десятичного числа только на одном определённом его выходе. На рис.9.11 приведено символическое изображение дешифратора и его таблица истинносити. Символ DC образован от английского слова Decoder. Слева показаны входы, на которых отмечены весовые коэффициенты двоичного кода, справа выходы десятичных чисел. На каждом входе образуется десятичное число при определенных комбинациях входного кода.
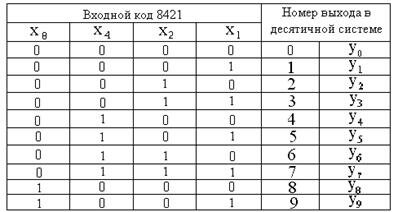
Рис.9.11. Символическое изображение дешифратора и его таблица истинности
Рассмотрим построение дешифратора по его таблице истинности.
Значения входных переменных определяются логическими выражениями:
y0 =8^4^ 2^1,
y1 =8^4^2^ x 1,
y2 =8^4^ x2 ^1,
y3 =8 ^4^ x2 ^ x1,
y4 =8 ^x4 ^2 ^1, (9.1)
y5 =8 ^ x4^2 ^ x1,
y6 =8 ^ x4^ x2 ^1,
y7 =8 ^ x4^ x2 ^ x1,
y8 = x8 ^4^2^1,
y9 = x 8 ^4 ^ 2^ x 1.
Используя логические выражения (9.1), построим логическую схему дешифратора.
На рис.9.12 показана логическая схема дешифратора, построенного на логических элементах И и инверторах НЕ.
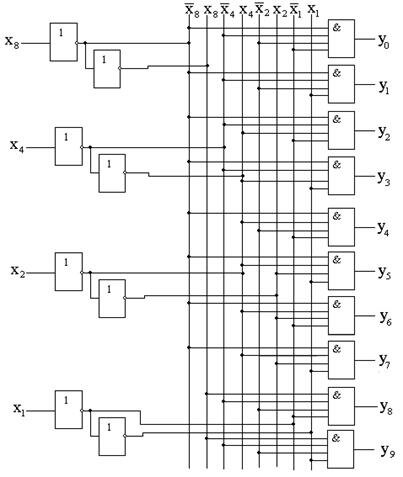
Рис.9.12. Логическая схема дешифратора
Как работает: алгоритмы шифрования
Допустим, вы уже сходили в удостоверяющий центр и получили на флешке сертификат и ключ электронной подписи. Теперь нужно скачать специальный софт, который и будет подписывать ваши документы и проверять чужие на подлинность.
Проблема в том, что ЭП основана на алгоритмах асимметричного шифрования, а их много: разложение на простые множители, дискретное логарифмирование, эллиптические кривые и множество других. Ключ из одного алгоритма не подойдёт для использования в другом, поэтому в России договорились использовать стандарт шифрования ГОСТ Р 34.10-2012, основанный на эллиптических кривых. Все государственные органы работают только с таким алгоритмом и не принимают другие ЭП.
Это значит, что нам нужен специальный софт, в котором уже есть этот алгоритм. Чаще всего используют КриптоПРО, реже — ViPNet CSP. С помощью этих программ можно подписать документы и проверить сертификаты на подлинность.
Достоинства аппаратного шифрования
Большое количество средств шифрования данных создаётся в виде специализированных физических устройств. Программные шифраторы, как правило, дешевле аппаратных и в ряде случаев способны обеспечить большую скорость обработки информации. Перечень достоинств аппаратных шифраторов:
- аппаратный датчик случайных чисел создаёт действительно случайные числа для формирования надёжных ключей шифрования и электронной цифровой подписи;
- аппаратная реализация криптоалгоритма гарантирует его целостность;
- шифрование и хранение ключей осуществляются в самой плате шифратора, а не в оперативной памяти компьютера;
- загрузка ключей в шифрующее устройство с электронных ключей Touch Memory (i-Button) и смарт-карт производится напрямую, а не через системную шину компьютера и ОЗУ, что исключает возможность перехвата ключей;
- с помощью аппаратных шифраторов можно реализовать системы разграничения доступа к компьютеру и защиты информации от несанкционированного доступа;
- применение специализированного процессора для выполнения всех вычислений разгружает центральный процессор компьютера; также можно установить нескольких аппаратных шифраторов на одном компьютере, что ещё более повышает скорость обработки информации (это преимущество присуще шифраторам для шины PCI);
- применение парафазных шин при создании шифрпроцессора исключает угрозу чтения ключевой информации по колебаниям электромагнитного излучения, возникающим при шифровании данных, в цепях «земля — питание» устройства.
- шифрование данных проходит быстрее чем в программно-аппаратно шифровании
При установке на компьютер специализированного шифровального оборудования будет возникать меньше проблем, чем при добавлении в системное программное обеспечение функций шифрования данных. В самом лучшем случае шифрование должно производиться так, чтобы пользователь не замечал его. Чтобы сделать это при помощи программных средств, они должны быть спрятаны достаточно глубоко в операционной системе. Проделать эту операцию безболезненно с отлаженной операционной системой очень непросто. Но подсоединить шифровальное устройство к персональному компьютеру или к модему сможет любой непрофессионал.
Почему этот шифр невзламываемый
Для начала договоримся, что под взломом мы понимаем прочтение этого сообщения без ключа. Если бы у нас был ключ, мы бы прочитали это сообщение почти сразу, и это уже не взлом.
Теперь посмотрим, почему без ключа этот шифр невозможно взломать.
- Каждый бит нашего исходного сообщения шифруется соответствующим битом, который берётся из ключа шифрования.
- Ключ шифрования — это случайные биты, такой «цифровой шум». Он не имеет смысла и в нём нет никакой логики. Каждый следующий бит может быть каким угодно.
- Шифрование происходит на самом низком уровне — на уровне битов. Мы даже не знаем, что перед нами: буквы, цифры, числа, картинки или аудио. Просто какой-то набор битов, которые выглядят как цифровой шум.
Единственный способ расшифровать целое сообщение — это получить целый ключ. Если мы получим лишь часть ключа, мы не сможем угадать или восстановить недостающую часть. Сколько ключа у нас есть — столько битов сообщения мы и расшифруем. Нет ключа — нет расшифровки.
Кодирование графики
Графическая информация может быть представлена в виде рисунков, схем, картинок или слайдов в PowerPoint. Любая картинка состоит из мелких точек — пикселей, которые могут быть окрашены в разный цвет. Цвет каждого пикселя кодируется и сохраняется, и в итоге мы получаем полноценное изображение.
Если картинка черно-белая, код каждого пикселя может быть либо единицей, либо нулем. Если используется 4 цвета, то код каждого из них состоит из двух цифр: 00, 01, 10 или 11. По этому принципу различают качество обработки любого изображения. Увеличение или уменьшение яркости также влияет на количество используемых цветов. В лучшем случае компьютер различает около 16 777 216 оттенков.

Система записи — это шифр
Если у нас есть девять коров, мы можем записать их как или как 9 × .
Почему 9 означает «девять»? И почему вообще есть такое слово? Почему такое количество мы называем этим словом? Вопрос философский, и короткий ответ — нам нужно одинаково называть числа, чтобы друг друга понимать. Слово «девять», цифра 9, а также остальные слова — это шифр, который мы выучили в школе, чтобы друг с другом общаться.
Допустим, к нашему стаду прибиваются еще . Теперь у нас — двенадцать коров, 12. Почему мы знаем, что 12 — это «двенадцать»? Потому что мы договорились так шифровать числа.
Нам очень легко расшифровывать записи типа 12, 1920, 100 500 и т. д. — мы к ним привыкли, мы учили это в школе. Но это шифр. 12 × — это не то же самое, что . Это некая абстракция, которой мы пользуемся, чтобы упростить себе счёт.
Выходит, что с шифрованием мои сообщения в безопасности?

Если кратко, то ответ будет утвердительным. Перехватить ваши сообщения по сети технически возможно, но без наличия самого устройства, с которого вы проводили отправку, это не имеет смысла.
Публичный ключ создается на основе закрытого, а значит сгенерировать его без устройства отправителя невозможно. Все работает в паре. Публичный ключ шифрует сообщение, а расшифровывается он с помощью закрытого ключа.
То есть в ситуации, когда правительственные органы власти требуют предоставления ключей шифрования, несложно понять, что технически это реализовать невозможно. В противном случае, придется организовать всенародную очередь со сдачей смартфонов на резервное копирование с целью достать приватный ключ каждого устройства.
У каждого мессенджера и сервиса этот ключ свой. Так что, беспокоиться о конфиденциальности при подобном шифровании не стоит. Простая отправка сообщения с точки зрения шифрования на самом деле выглядит не так просто.

iPhones.ru
Рассказываем о процессах, которые мы никогда не увидим.