Последовательная схема
Последовательная цепь LC
В последовательной конфигурации LC-цепи катушка индуктивности (L) и конденсатор (C) соединены последовательно, как показано здесь. Общее напряжение V на открытых клеммах — это просто сумма напряжения на катушке индуктивности и напряжения на конденсаторе. Ток I на положительном выводе схемы равен току через конденсатор и катушку индуктивности.
- Vзнак равноVL+VC,язнак равнояLзнак равнояC.{\ displaystyle {\ begin {align} V & = V_ {L} + V_ {C}, \\ I & = I_ {L} = I_ {C}. \ end {align}}}
Резонанс
Величина X L индуктивного реактивного сопротивления увеличивается с увеличением частоты, а величина X C уменьшается с увеличением частоты. На одной конкретной частоте эти два реактивных сопротивления равны по величине, но противоположны по знаку; эта частота называется резонансной частотой f для данной цепи.
Следовательно, при резонансе
- ИксLзнак равноИксC,ωLзнак равно1ωC.{\ displaystyle {\ begin {align} X_ {L} & = X_ {C}, \\\ omega L & = {\ frac {1} {\ omega C}}. \ end {выравнивается}}}
Решая относительно ω , имеем
- ωзнак равноωзнак равно1LC,{\ displaystyle \ omega = \ omega _ {0} = {\ frac {1} {\ sqrt {LC}}},}
которая определяется как резонансная угловая частота контура. Преобразуя угловую частоту (в радианах в секунду) в частоту (в герцах), мы получаем
- жзнак равноω2πзнак равно12πLC.{\ displaystyle f_ {0} = {\ frac {\ omega _ {0}} {2 \ pi}} = {\ frac {1} {2 \ pi {\ sqrt {LC}}}}.}
В последовательной конфигурации X C и X L компенсируют друг друга. В реальных, а не идеализированных компонентах току противодействует, в основном, сопротивление обмоток катушки. Таким образом, ток, подаваемый в последовательный резонансный контур, максимален при резонансе.
- В пределе f → f ток максимален. Сопротивление цепи минимальное. В этом состоянии цепь называется приемной цепью.
- Для е < е , X L «- X C . Следовательно, цепь емкостная.
- Для е > е , X L »- X C . Следовательно, цепь индуктивна.
Импеданс
В последовательной конфигурации резонанс возникает, когда комплексное электрическое сопротивление цепи приближается к нулю.
Сначала рассмотрим импеданс последовательной LC-цепи. Полный импеданс определяется суммой индуктивного и емкостного сопротивлений:
- Zзнак равноZL+ZC.{\ displaystyle Z = Z_ {L} + Z_ {C}.}
Записывая индуктивное сопротивление как Z L = jωL и емкостное сопротивление как Z C =1jωC и замена дает
- Z(ω)знак равноjωL+1jωC.{\ Displaystyle Z (\ omega) = j \ omega L + {\ frac {1} {j \ omega C}}.}
Запись этого выражения под общим знаменателем дает
- Z(ω)знак равноj(ω2LC-1ωC).{\ displaystyle Z (\ omega) = j \ left ({\ frac {\ omega ^ {2} LC-1} {\ omega C}} \ right).}
Наконец, определяя собственную угловую частоту как
- ωзнак равно1LC,{\ displaystyle \ omega _ {0} = {\ frac {1} {\ sqrt {LC}}},}
импеданс становится
- Z(ω)знак равноjL(ω2-ω2ω).{\ displaystyle Z (\ omega) = jL \ left ({\ frac {\ omega ^ {2} — \ omega _ {0} ^ {2}} {\ omega}} \ right).}
Числитель означает, что в пределе ω → ± ω полный импеданс Z будет равен нулю, а в противном случае отличен от нуля. Следовательно, последовательный LC-контур при последовательном включении с нагрузкой будет действовать как полосовой фильтр, имеющий нулевой импеданс на резонансной частоте LC-контура.
Резонанс токов в параллельном колебательном контуре
Рассмотрим случай параллельного соединения колебательного контура с источником тока (рис. 1) и посмотрим, каково будет сопротивление контура для токов различных частот в этом случае. Если частота тока невелика (ниже резонансной), то почти весь ток пойдет по наиболее легкому для него пути — через индуктивную ветвь; сопротивление контура при низких частотах будет небольшим по величине и индуктивным по своему характеру.
Для токов высоких частот (выше резонансной) более легким путем будет путь через емкостную ветвь, и, следовательно, сопротивление контура будет также небольшим по величине, но емкостным по характеру.
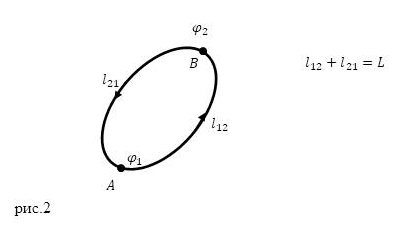
При резонансной частоте, когда емкостное сопротивление равно индуктивному, путь для тока будет одинаково трудным через обе ветви. Мы знаем, что при параллельном соединении двух равных сопротивлений общее сопротивление равняется половине любого из них. Поэтому, казалось бы, что сопротивление контура при резонансе должно равняться половине одного из реактивных сопротивлений. Однако, не следует забывать, что мы имеет дело, с сопротивлениями, хотя и одинаковыми по величине, но имеющими принципиально различный характер. Это различие проявляется в том, что токи в индуктивной и емкостной ветвях контура сдвинуты по фазе друг относительно друга на 180°. Отсюда непосредственно следует, что в неразветвленной части цепи всегда протекает не суммарный, а разностный ток (рис. 1).
Рисунок 1. Токи при параллельном резонансе. В неразвлетвленной части цепи протекает не скммарный, а разностный ток.
Поэтому при резонансе, когда токи в емкостной и индуктивной ветвях равны между собой, ток в неразветвленной части цепи будет равен нулю, какое бы напряжение мы ни прилагали к контуру. При резонансе между точками АВ цепь будет казаться разорванной, т. е. сопротивление ее между этими точками будет бесконечно велико, а отнюдь не будет равным половине одного из реактивных сопротивлений. Практически бесконечно большого сопротивления контура при резонансе не бывает, так как из-за наличия активного сопротивления в контуре (сопротивление провода катушки) сдвиг фаз токов никогда не может быть равным точно 180°.
Однако активное сопротивление катушки обычно бывает много меньше ее индуктивного сопротивления, и поэтому сопротивление колебательного контура при резонансе может достигать очень больших величин.
Сопротивление колебательного контура при параллельном резонансе равно:
где L выражено в гн, С—в ф, RL—в ом.
Полное сопротивление колебательного контура при резонансе является чисто активным в силу того обстоятельства, что индуктивное и емкостное сопротивления взаимно компенсируются.
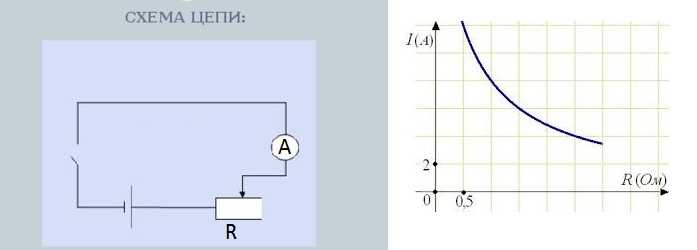
Кривые изменения полного сопротивления колебательного контура между точками АВ при изменении частоты тока приведены на рис. 2,б.
Рисунок 2. Резонанс токов. а) — схема и обозначения; б) — график полного сопротивления.
При параллельном резонансе токи ,в ветвях контура достигают наибольшей величины; поэтому параллельный резонанс называется резонансом токов.
Явление резонанса имеет огромнейшее значение в радиотехнике. На земном шаре имеется большое количество передающих радиостанций. Передачи всех этих радиостанций распространяются в эфипе и все одновременно принимаются приемной антенной. Нетрудно представить себе, каким получилось бы нагромождение друг на друга передач, если бы мы не могли выделить из этого хаоса только одну нужную нам. Вот тут-то на помощь приходит явление резонанса. Передающие радиостанции излучают в пространство электромагнитную энергию на различных частотах, мы же, настраивая контуры нашего приемника в резонанс с той или иной частотой, тем самым выбираем нужную нам передачу.
Похожие материалы:
- Индуктивное сопротивление катушки
- Катушка индуктивности в цепи переменного тока
- Конденсатор в цепи переменного тока. Емкостное сопротивление конденсатора.
- Активное сопротивление цепи переменного тока
- Полное сопротивление цепи переменного тока
- Явление резонанса
- Закон Ома для переменного тока
- Резонанс напряжений в последовательном колебательном контуре
- Пульсирующий ток
- Несинусоидальный ток
Что такое ёмкость конденсатора?
Ёмкость конденсатора представляет собой отношение заряда конденсатора к напряжению, под которым он находится. Посчитать эту величину можно очень просто с помощью математической формулы:
C = (e0*S)/d, гдеe0 — диэлектрическая проницаемость материала диэлектрика (табличная величина), S — площадь обкладок конденсатора, d — расстояние между пластинами.
Зависимость ёмкости конденсатора от расстояния между обкладками объясняется явлением электростатической индукции: чем меньше расстояние между пластинами, тем сильнее они влияют друг на друга (по закону Кулона), тем больше заряд обкладок и меньше напряжение. А при уменьшении напряжения увеличивается значение ёмкости, так как её также можно описать следующей формулой:
C = q/U, гдеq — заряд в кулонах.
Стоит поговорить о единицах измерения этой величины. Ёмкость измеряется в фарадах. 1 фарад — достаточно большая величина, поэтому существующие конденсаторы (но не ионисторы) имеют ёмкость, измеряемую в пикофарадах (одна триллионная фарада).
Создание свободных колебаний в идеальном колебательном контуре
Для внешне замкнутой цепи, состоящей из идеальных (без потерь) компонентов, содержащих определенное количество энергии, возникает периодический процесс. В целях описания состояние в произвольно выбранный момент времени установлено как начальное состояние.
U : напряжение; I : ток; W : энергия
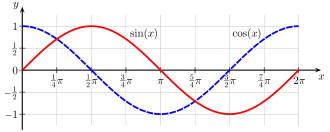
Кривая напряжения (пунктирная синяя) и кривая тока (красная линия) в резонансном контуре
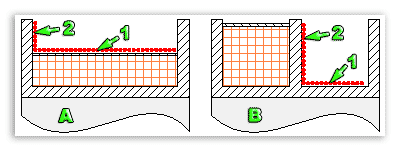
- Во-первых, пусть катушка будет без магнитного потока. Конденсатор заряжен, и вся энергия колебательного контура хранится в его электрическом поле. Ток через катушку еще не течет. (Изображение 1)
- Из-за напряжения на конденсаторе, которое также падает на катушке, ток начинает течь, но не увеличивается внезапно. Согласно правилу Ленца , изменение тока вызывает напряжение, которое противодействует его изменению. Это означает, что сила тока и магнитный поток увеличиваются только медленно (сначала линейно со временем). По мере увеличения тока заряд конденсатора со временем уменьшается, что в то же время снижает его напряжение. По мере уменьшения напряжения увеличение тока уменьшается.
- Когда напряжение упало до нуля, ток больше не увеличивается и, таким образом, достигает своего максимума. В этот момент напряженность магнитного поля катушки наибольшая, и конденсатор полностью разряжен. Теперь вся энергия хранится в магнитном поле катушки. (Рисунок 2)
- Когда катушка обесточена, ток продолжает стабильно течь, потому что, как и магнитный поток, он не может резко измениться. Ток начинает заряжать конденсатор в обратном направлении. В нем нарастает противодавление (изначально линейное со временем). Это напряжение, которое увеличивается с отрицательным знаком, похоже на напряжение в катушке, которое, согласно правилам индукции, со временем уменьшает магнитный поток, что в то же время снижает силу тока. По мере уменьшения протекания тока зарядка конденсатора и рост его отрицательного напряжения замедляются.
- Когда ток упал до нуля, величина напряжения больше не увеличивается и, таким образом, достигает своего максимума. Конденсатор восстанавливает свой первоначальный заряд, но с противоположной полярностью. Вся энергия магнитного поля была преобразована обратно в энергию электрического поля. (Рисунок 3)
- Эти процессы продолжаются в обратном направлении. (Изображение 4, затем снова изображение 1)
При непрерывном повторении кривая напряжения устанавливается в соответствии с функцией косинуса ; текущая кривая следует синусоидальной функции. Переход от рисунка 1 к рисунку 2 соответствует в функциях диапазону x = 0… π / 2; переход от изображения 2 к изображению 3 выполняется как в области x = π / 2… π, от изображения 3 через изображение 4 к изображению 1 как в x = π… 2π.
Резонанс напряжений
Давайте возьмем другие параметры катушки и конденсатора и посмотрим, что у нас происходит на самих радиоэлементах. Нам ведь надо досконально все выяснить ;-). Беру катушку индуктивности с индуктивностью в 22 микрогенри:

и конденсатор в 1000 пФ

Из них собираю последовательный колебательный контур. Итак, чтобы поймать резонанс, я не буду в схему добавлять резистор. Поступлю более хитрее.
Так как мой генератор частоты китайский и маломощный, то при резонансе у нас в цепи остается только активное сопротивление потерь R. В сумме получается все равно маленькое значение сопротивления, поэтому ток при резонансе достигает максимальных значений. В результате этого, на внутреннем сопротивлении генератора частоты падает приличное напряжение и выдаваемая амплитуда частоты генератора падает. Я буду ловить минимальное значение этой амплитуды. Следовательно это и будет резонанс колебательного контура. Перегружать генератор – это не есть хорошо, но что не сделаешь ради науки!
Ну что же, приступим ;-). Давайте сначала посчитаем резонансную частоту по формуле Томсона. Для этого я открываю онлайн калькулятор на просторах интернета и быстренько высчитываю эту частоту. У меня получилось 1,073 Мегагерц.
Ловлю резонанс на генераторе частоты по его минимальным значениям амплитуды. Получилось как-то вот так:
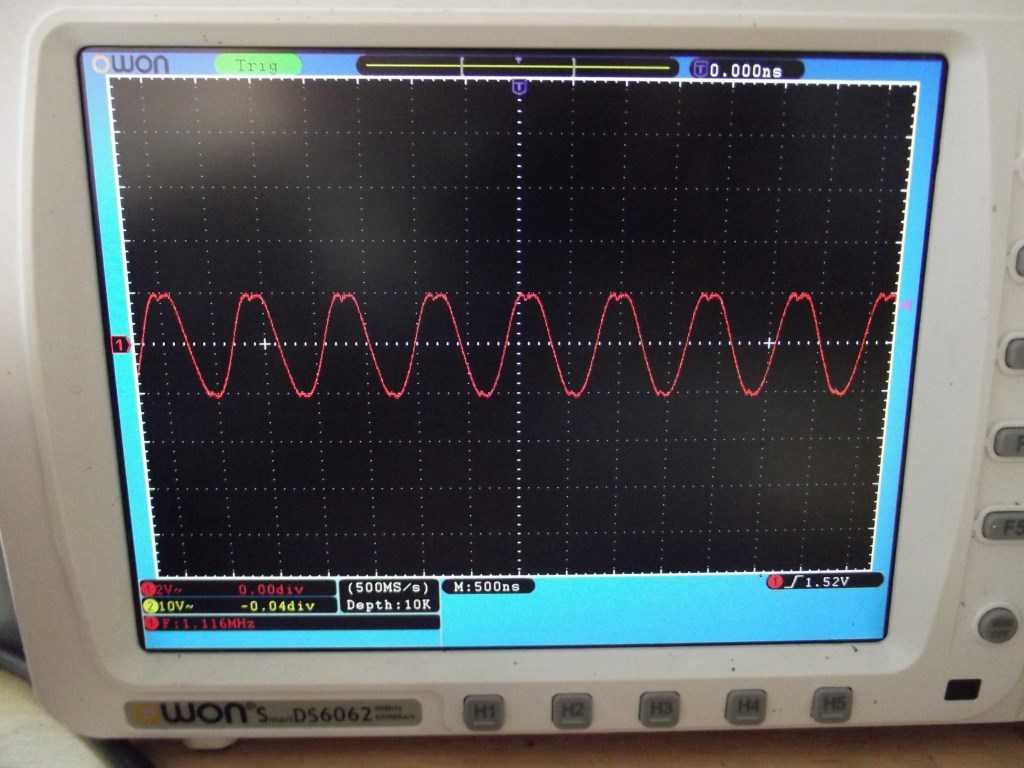
Размах амплитуды 4 Вольта
Хотя на генераторе частоты размах более 17 Вольт! Вот так вот сильно просело напряжение. И как видите, резонансная частота получилась чуток другая, чем расчетная: 1,109 Мегагерц.

Теперь небольшой прикол 😉
Вот этот сигнал мы подаем на наш последовательный колебательный контур:
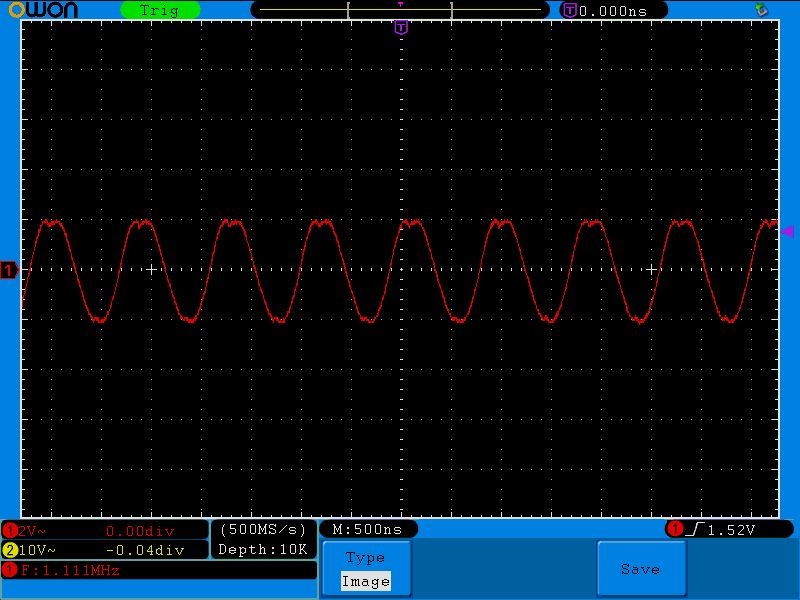
Как видите, мой генератор не в силах выдать большую силу тока в колебательный контур на резонансной частоте, поэтому сигнал получился даже чуть искаженным на пиках.
Ну а теперь самое интересное. Давайте замеряем падение напряжения на конденсаторе и катушке на резонансной частоте. То есть это будет выглядеть вот так:
Смотрим напряжение на конденсаторе:
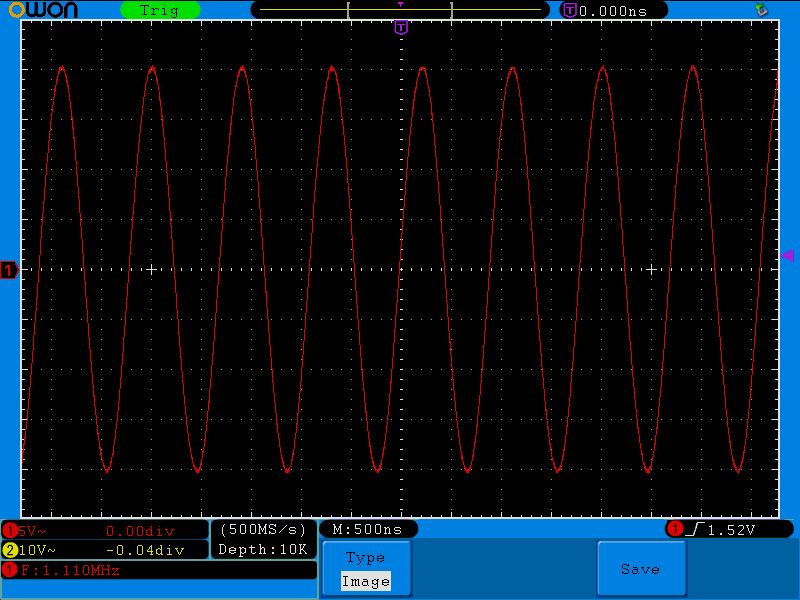
Размах амплитуды 20 Вольт (5х4)! Откуда? Ведь подавали мы на колебательный контур синус с частотой в 2 Вольта!

Ладно, может с осциллографом что-то произошло?. Давайте замеряем напряжение на катушке:
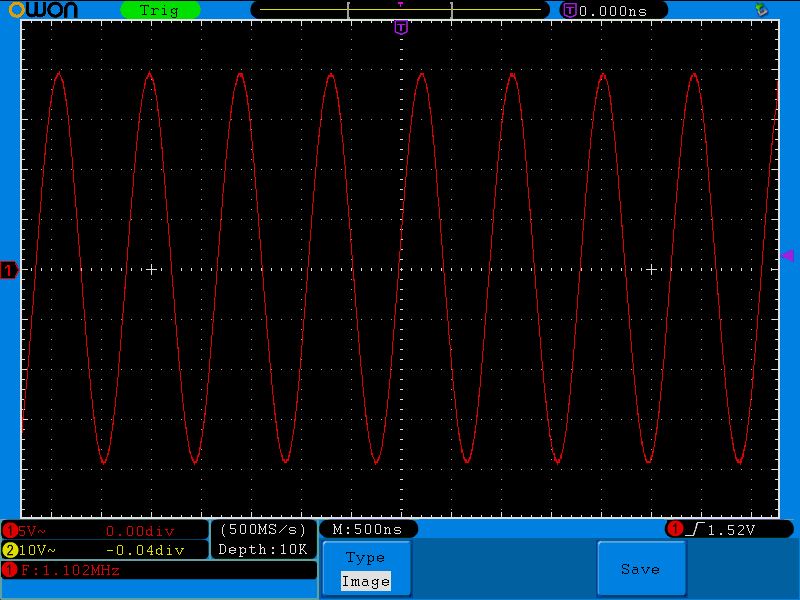
Народ! Халява!!! Подали 2 Вольта с генератора, а получили 20 Вольт и на катушке и на конденсаторе! Выигрыш энергии в 10 раз! Успевай только снимать энергию с конденсатора или с катушки!
Ну ладно раз такое дело… беру лампочку от мопеда на 12 Вольт и цепляю ее к конденсатору или катушке. Лампочке ведь вроде как по-барабану на какой частоте работать и какой ток кушать. Выставляю амплитуду, чтобы на катушке или конденсаторе было где то Вольт 20 так как среднеквадратичное напряжение будет где-то Вольт 14, и цепляю поочередно к ним лампочку:


Как видите – полный ноль. Лампочка гореть не собирается, так что побрейтесь фанаты халявной энергии). Вы ведь не забыли, что мощность определяется произведением силы тока на напряжение? Напряжения вроде как-бы хватает, а вот силы тока – увы! Поэтому, последовательный колебательный контур носит также название узкополосного (резонансного) усилителя напряжения, а не мощности!
Объяснение резонанса напряжения
При резонансе напряжение на катушке и на конденсаторе оказались намного больше, чем то, которое мы подавали на колебательный контур. В данном случае у нас получилось в 10 раз больше. Почему же напряжение на катушке при резонансе равняется напряжению на конденсаторе. Это легко объясняется. Так как в последовательном колебательном контуре катушка и кондер идут друг за другом, следовательно, в цепи протекает одна и та же сила тока.
При резонансе реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора. Получаем по правилу шунта, что на катушке у нас падает напряжение UL = IXL , а на конденсаторе UC = IXC . А так как при резонансе у нас XL = XC , то получаем что UL = UC , ток ведь в цепи один и тот же ;-). Поэтому резонанс в последовательном колебательном контуре называют также резонансом напряжений, так как напряжение на катушке на резонансной частоте равняется напряжению на конденсаторе.
Резонанс в реальных цепях
Для изучения описанных процессов надо собрать контур из соответствующих компонентов. Придется подготовить генератор с изменяющейся частотой выходного сигнала, осциллограф и другие измерительные инструменты. Чтобы получить достоверные результаты без лишних трудностей, пользуются специализированным программным обеспечением.
Теория и практика
В левой части рисунка размещены схема и амплитуда сигнала на выходе при подключении к выводам конденсатора параллельного контура. В правой – снимок экрана измерительной аппаратуры. Несложно убедиться в идентичности колебаний.
К сведению. С помощью ПО выполняют десятки экспериментов быстро и точно в обычных домашних условиях. Этот способ значительно упрощает создание электрических схем с оптимальными параметрами.
Параметры и электрические величины при резонансе
Теперь давайте по порядку выведем значения параметров и электрических величин при резонансе параллельной цепи RLC.
Резонансная частота
Мы знаем, что резонансная частота f r
— это частота, на которой возникает резонанс. В параллельной RLC цепи резонанс возникает, когда мнимый член допуска Y равен нулю. т.е. значение frac1XC− frac1XL должно быть равно нулю
Rightarrow frac1XC= frac1XL
RightarrowXL=XC
Вышеуказанное условие резонанса такое же, как и в последовательной цепи RLC. Таким образом, резонансная частота f r
будет одинаковой как в последовательной RLC-цепи, так и в параллельной RLC-схеме.
Следовательно, резонансная частота f r
параллельной RLC-схемы равна
fr= frac12 pi sqrtLC
Куда,
- L — индуктивность индуктора.
- С — емкость конденсатора.
Резонансная частота f r
параллельной цепи RLC зависит только от индуктивностиL и емкостиC. Но это не зависит от сопротивленияR.
впуск
Мы получили допуск Y
параллельной цепи RLC как
Y= frac1R+j lgroup frac1XC− frac1XL rgroup
Замените XL=XC в приведенном выше уравнении.
Y= frac1R+j lgroup frac1XC− frac1XC rgroup
RightarrowY= frac1R+j(0)
RightarrowY= frac1R
При резонансе вход
Y параллельной цепи RLC равен обратной величине сопротивления R. т.е. mathbf mathitY= frac1R
Напряжение на каждом элементе
Замените frac1XC− frac1XL=0 в уравнении 1
I=V
RightarrowI= fracVR
RightarrowV=IR
Следовательно, напряжение
на всех элементах параллельной цепи RLC при резонансе равноV = IR .
При резонансе допуск параллельной цепи RLC достигает минимального значения. Следовательно, максимальное напряжение
присутствует на каждом элементе этой цепи в резонансе.
Ток, протекающий через резистор
Ток, протекающий через резистор
IR= fracVR
Подставим значение V
в приведенное выше уравнение.
IR= fracIRR
RightarrowIR=I
Следовательно, ток, протекающий через резистор
в резонансе, составляет mathbf mathitIR=I.
Ток, протекающий через индуктор
Ток, протекающий через индуктор
IL= fracVjXL
Подставим значение V
в приведенное выше уравнение.
IL= fracIRjXL
RightarrowIL=−j lgroup fracRXL rgroupI
RightarrowIL=−jQI
Следовательно, ток, протекающий через индуктор
в резонансе, равен IL=−jQI.
Итак, величина
тока, протекающего через индуктор в резонансе, будет
$$ | I_L | = QI $$
Где Q — фактор качества,
а его значение равно fracRXL
Формула резонанса
Для параллельного колебательного контура также работает формула Томсона для резонансной частоты как и для последовательного колебательного контура:
где
F – это резонансная частота контура, Герцы
L – индуктивность катушки, Генри
С – емкость конденсатора, Фарады
Ладно, ближе к делу. Берем паяльник в руки и спаиваем катушку и конденсатор параллельно. Катушка на 22 мкГн, а конденсатор на 1000пФ.
Итак, реальная схема этого контура будет вот такая:
Для того, чтобы все показать наглядно и понятно, давайте добавим к контуру последовательно резистор на 1 КОм и соберем вот такую схему:
.JPG»]
На генераторе мы будет менять частоту, а с клемм X1 и X2 мы будем снимать напряжение и смотреть его на осциллографе.
Нетрудно догадаться, что у нас сопротивление параллельного колебательного контура будет зависеть от частоты генератора, так как в этом колебательном контуре мы видим два радиоэлемента, чьи реактивные сопротивления напрямую зависит от частоты, поэтому заменим колебательный контур эквивалентным сопротивлением контура Rкон.
Упрощенная схема будет выглядеть вот так:
Интересно, на что похожа эта схема? Не на делитель ли напряжения? Именно! Итак, вспоминаем правило делителя напряжения: на меньшем сопротивлении падает меньшее напряжение, на бОльшем сопротивлении падает бОльшее напряжение. Какой вывод можно сделать применительно к нашему колебательному контуру? Да все просто: на резонансной частоте сопротивление Rкон будет максимальным, вследствие чего у нас на этом сопротивлении “упадет” бОльшее напряжение.
Начинаем наш опыт. Поднимаем частоту на генераторе, начиная с самых маленьких частот.
Как вы видите, на колебательном контуре “падает” малое напряжение, значит, по правилу делителя напряжения, можно сказать, что сейчас у контура малое сопротивление Rкон
Добавляем частоту. 11,4 Килогерца
Как вы видите, напряжение на контуре поднялось. Это значит, что сопротивление колебательного контура увеличилось.
Добавляем еще частоту. 50 Килогерц
Заметьте, напряжение на контуре повысилось еще больше. Значит его сопротивление еще больше увеличилось.
723 Килогерца
Обратите внимание на цену деления одного квадратика по вертикали, по сравнению с прошлым опытом. Там было 20мВ на один квадратик, а сейчас уже 500 мВ на один квадратик
Напряжение выросло, так как сопротивление колебательного контура стало еще больше.
И вот я поймал такую частоту, на которой получилось максимальное напряжение на колебательном контуре
Обратите внимание на цену деления по вертикали. Она равняется двум Вольтам
Дальнейшее увеличение частоты приводит к тому, что напряжение начинает падать:
Снова добавляем частоту и видим, что напряжение стало еще меньше:
Давайте более подробно рассмотрим эту осциллограмму, когда у нас было максимальное напряжение с контура.
Что здесь у нас произошло?
Так как на этой частоте был всплеск напряжения, следовательно, на этой частоте параллельный колебательный контур имел самое высокое сопротивление Rкон. На этой частоте ХL = ХС. Потом с ростом частоты сопротивление контура снова упало. Это и есть то самое резонансное сопротивление контура, которое выражается формулой:
Шпаргалки по электротехнике и электронике — Понятие о резонанс токов
Sunday, 24 January 2016 04:20
administrator
| Cмотрите так же… |
|---|
| Шпаргалки по электротехнике и электронике |
| Закон Ома для замкнутой цепи и для участка цепи |
| Законы Кирхгофа для цепи постоянного тока |
| Расчет простых цепей при различных схемах соединения потребителей |
| Понятие о сложной электрической цепи |
| Мощность, работа и потери КПД электрических цепей |
| Синусоидальный ток и его основные параметры |
| Способы представления синусоидального тока |
| Резисторное сопротивление в цепи синусоидального тока |
| Конденсатор в цепи синусоидального тока |
| Индуктивность в электрической цепи |
| Закон электромагнитной индукции |
| Индуктивность в цепи синусоидального тока |
| Взаимоиндуктивность в магнитосвязанных цепях |
| Законы Кирхгофа для цепей синусоидального тока |
| Закон Ома и сопротивления цепи синусоидального тока с последовательным соединением элементов R, L,C |
| Понятие о резонансе напряжений |
| Резонанс напряжений и его признаки |
| Закон Ома и проводимость цепи синусоидального тока с параллельным соединением ветвей R-L, L-C |
| Понятие о резонанс токов |
| Мгновенная мощь цепи синусоидального тока |
| Активная, реактивная и полная мощность цепей синусоидального тока |
| Коэффициент мощности и его экономическое значение |
| Получение трехфазной системы ЭДС и способы представления |
| Соединения обмоток трехфазных генераторов |
| Соединения приемников в трехфазных цепях |
| Мощность трехфазных цепей |
| Трансформаторы |
| Работа трансформаторов в различных режимах |
| Потери и КПД трансформаторов |
| Устройство, схемы и группы соединения обмоток трехфазных трансформаторов |
| Назначение, схема и работа автотрансформатора |
| Назначение, схема и работа импульсного трансформатора |
| Машины постоянного тока |
| Асинхронные электродвигатели |
| Синхронные электродвигатели |
| Пускорегулирующая аппаратура |
| Выбор типа и мощности электродвигателя |
| Провода и кабели, выбор сечения проводов |
| Защитное заземление |
| Электронно-дырочный переход |
| Диоды, тиристоры |
| Транзисторы |
| Основные логические операции и их реализация |
| Триггеры |
| Однофазные неуправляемые выпрямители |
| Трехфазные выпрямители: нулевой, мостовой |
| Фильтры(C, L, LC, RC), коэффициент пульсаций |
| Однофазные и трехфазные управляемые выпрямители |
| All Pages |
Page 20 of 49
Понятие о резонанс токов. Условия его возникновения и способы осуществления
Резонанс токов — резонанс, происходящий в параллельном колебательном контуре при его подключении к источнику напряжения, частота которого совпадает с собственной частотой контура.
Условие резонанса токов: , .
В1 – реактивная проводимость первой ветви,
В2 – реактивная проводимость второй ветви.
Способ возбуждения колебаний в электрическом контуре, заключающийся в генерации колебаний, за счет регулирования сигнала, управляющего возбуждением колебаний.
Резонанс токов и его признаки
Режим, при котором в цепи, содержащей параллельные ветви с индуктивными и емкостными элементами, ток неразветвленного участка цепи совпадает по фазе с напряжением (φ=0), называют резонансом токов.
Признаки резонанса токов:
Реактивные составляющие токов ветвей равны IPC = IPL и находятся в противофазе в случае, когда напряжение на входе чисто активное;
Токи ветвей превышают общий ток цепи, который имеет минимальное значение и совпадают по фазе.
Last Updated on Sunday, 24 January 2016 04:34
Из чего состоит заземление
- Внешний контур заземления. Располагается за пределами помещений, непосредственно в грунте. Представляет собой пространственную конструкцию из электродов (заземлителей), соединенных между собой неразделимым проводником.
- Внутренний контур заземления. Токопроводящая шина, размещенная внутри здания. Охватывает периметр каждого помещения. К этому устройству подсоединяются все электроустановки. Вместо внутреннего контура может быть установлен щиток заземления.
- Заземляющие проводники. Соединительные линии, предназначенные для подключения электроустановок непосредственно к заземлителю, или внутреннему контуру заземления.
Рассмотри эти компоненты подробнее.
Внешний, или наружный контур
Монтаж контура заземления зависит от внешних условий. Прежде чем начать расчет, и выполнить проектный чертеж, необходимо знать параметры грунта, в котором будут установлены заземлители. Если вы сами строили дом, эти характеристики известны. В противном случае лучше вызвать геодезистов, для получения заключения по грунту.
Какие бывают грунты, и как они влияют на качество заземления? Примерное удельное сопротивление каждого типа грунта. Чем оно ниже, тем лучше проводимость.
- Глина пластичная, торф = 20–30 Ωм·м
- Суглинок пластичный, зольные грунты, пепел, классическая садовая земля = 30–40 Ом·м
- Чернозем, глинистые сланцы, полутвердая глина = 50–60 Ом·м
Это лучшая среда для того, чтобы установить наружный контур заземления. Сопротивление растекания тока будет достаточно низким даже при малом содержании влаги. А в этих грунтах естественная влажность обычно выше среднего.
Полутвердый суглинок, смесь глины и песка, влажная супесь — 100–150 Ом·м
Сопротивление немного выше, но при нормальной влажности параметры заземления не выйдут за нормативы. Если в регионе установки установится продолжительная сухая погода, необходимо принимать меры к принудительному увлажнению мест установки заземлителей.
Глинистый гравий, супесок, влажный (постоянно) песок = 300–500 Ом·м
Гравий, скала, сухой песок – даже при высокой общей влажности, заземление в такой почве будет неэффективным. Для соблюдения нормативов, придется устанавливать глубинные заземлители.
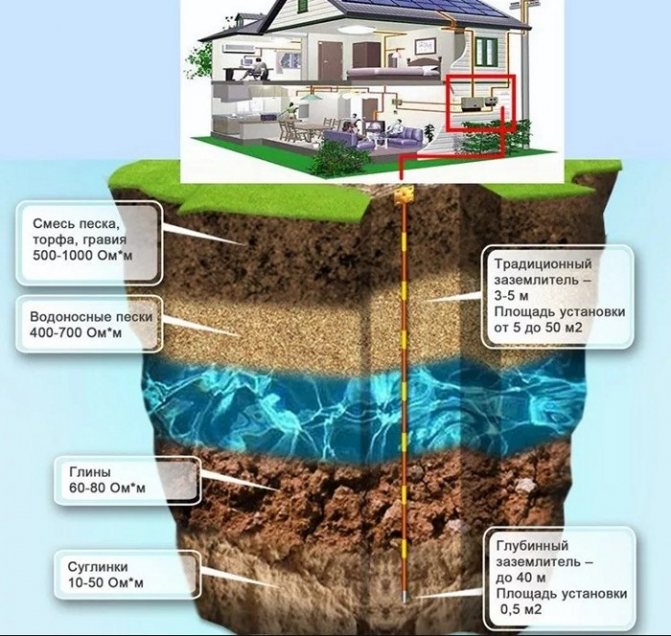
Многие владельцы объектов, экономя «на спичках», просто не понимают, для чего нужен контур заземления. Его задача при соединении фазы с землей обеспечить максимальную величину тока короткого замыкания. Только в этом случае быстро сработают устройства защитного отключения. Этого невозможно достичь, если сопротивление растекания тока будет высоким.
Определившись с грунтом, вы сможете выбрать тип, и самое главное — размер заземлителей. Предварительный расчет параметров можно выполнить по формуле:
Расчет приведен для вертикально установленных заземлителей.
Расшифровка величин формулы:
- R0 — полученное после вычисления сопротивление одного заземлителя (электрода) в омах.
- Рэкв — удельное сопротивление грунта, см. информацию выше.
- L — общая длина каждого электрода в контуре.
- d — диаметр электрода (если сечение круглое).
- Т — вычисленное расстояние от центра электрода до поверхности земли.
Задавая известные данные, а также меняя соотношение величин, вы должны добиться значения для одного электрода порядка 30 Ом.
Если установка вертикальных заземлителей невозможна (по причине качества грунта), можно рассчитать величину сопротивления горизонтальных заземлителей.
Поэтому лучше потратить больше времени на забивание вертикальных стержней, чем следить за барометром и влажностью воздуха.
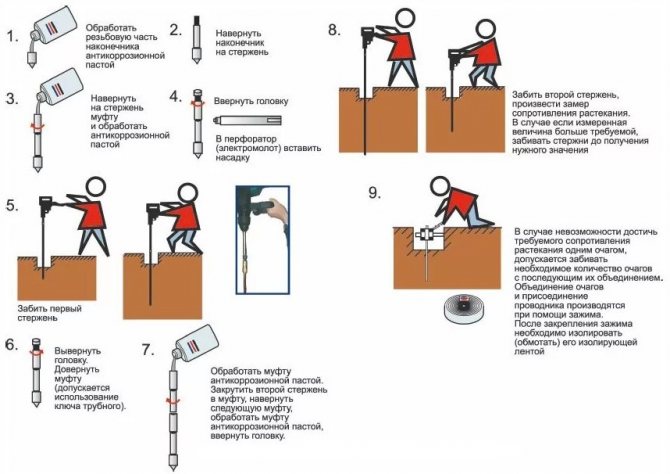
И все же приводим формулу расчета горизонтальных заземлителей.
Соответственно, расшифровка дополнительных величин:
- Rв — полученное после вычисления сопротивление одного заземлителя (электрода) в омах.
- b — ширина электрода — заземлителя.
- ψ — коэффициент, зависящий от погодного сезона. Данные можно взять в таблице:
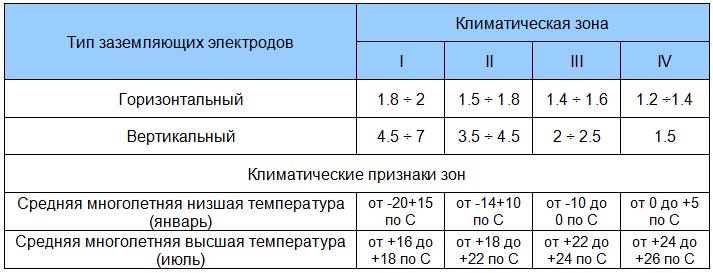
ɳГ — так называемый коэффициент спроса горизонтально расположенных электродов. Не вдаваясь в подробности, получаем цифры из таблицы на иллюстрации:
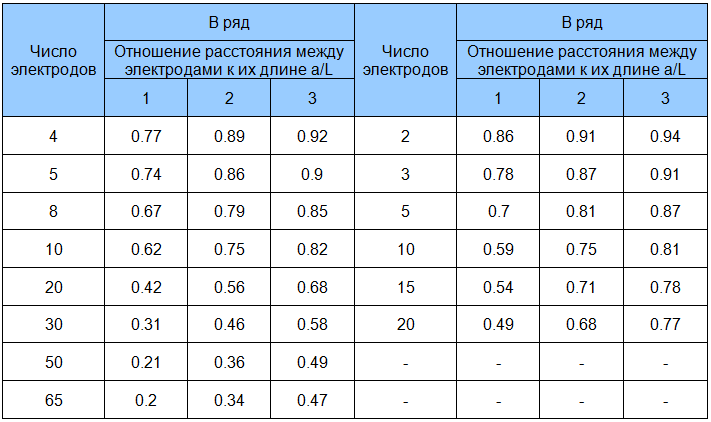
Предварительный расчет сопротивления необходим не только для правильного планирования закупок материала: хотя будет обидно, если вам не хватит для завершения работ, пары метров электрода, а до магазина несколько десятков километров. Более-менее аккуратно оформленный план, расчеты и чертежи, пригодятся для решения бюрократических вопросов: при подписании документов о приемке объекта, или составлении ТУ с компанией энергосбыта.
Разумеется, никакой инженер не подпишет бумаги только на основании пусть и красиво исполненных чертежей. Будут произведены замеры сопротивления растекания.
Далее расскажем о том, как добиться правильных характеристик внешнего контура заземления.
Резонансная частота
При подаче на два КК (параллельного и последовательного) переменного напряжения с изменяющейся частотой их реактивные сопротивления C и L будут меняться. Изменения происходят следующим образом:
- с увеличением f – ёмкостное сопротивление уменьшается, а индуктивное увеличивается;
- с уменьшением f – ёмкостное сопротивление увеличивается, а индуктивное уменьшается.
Резонанс — что это такое Частота, при которой реактивные сопротивления обоих элементов контура равны, называется резонансной.
Важно! При fрез сопротивление параллельного КК будет максимальным, а последовательного КК – минимальным. Резонансная частота формула, которой имеет вид:
Резонансная частота формула, которой имеет вид:
fрез = 1/2π*√L*C,
где:
- L – индуктивность, Гн;
- C – ёмкость, Ф.
Подставляя известные значения ёмкости и индуктивности в формулу резонансной частоты колебательного контура любой конфигурации, можно рассчитать этот параметр.
Для определения периода колебаний КК и частоты резонанса можно воспользоваться онлайн калькулятором на соответствующем портале в сети. Профессиональная программа имеет несложный интерфейс.
Пример интерфейса онлайн калькулятора LC-контура
Амплитуда, период и частота
Если подвесить одновременно два груза на две разные нити и запустить их, то можно заметить, что расстояние отклонения груза от среднего положения до крайнего — разное.
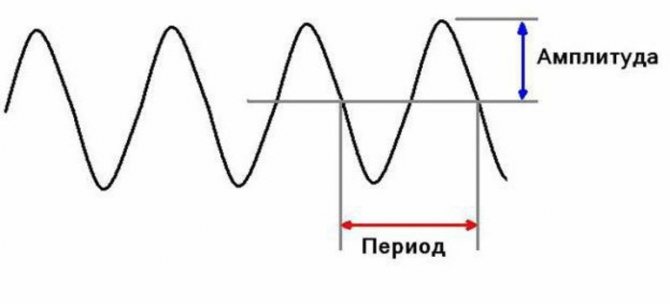
Это величина носит название амплитуды. Обозначается буквой А и измеряется в системе Си в метрах. Также для обозначения подобного движения применяются следующие термины:
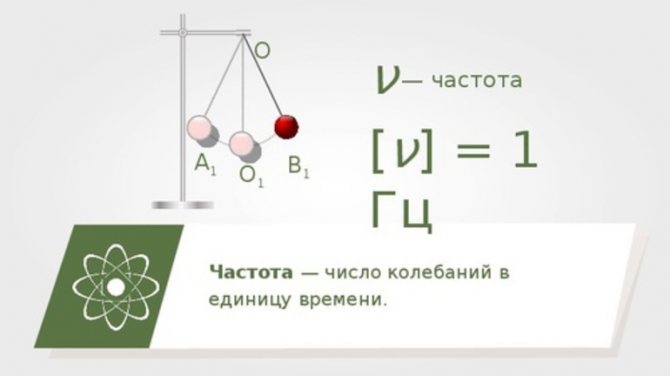
- Время, за которое маятник приходит в одно и то же положение, называется периодом колебаний.
- Количество колебаний в единицу времени представляет собой частоту. Она измеряется в Герцах (Гц). Имеет обратную зависимость от периода.
- Циклическая частота колебаний (угловая, круговая) представляет собой количество колебаний за 2 π секунд. Обозначается греческой буквой омега. Она вводится для упрощения расчетов в теоретической физике и электронике. Единица измерения циклической частоты рад/с.
- Если имеется два графика функций с одинаковой частотой, но сдвинуты относительно друг друга, то различна их фаза колебаний.
Выделяют понятие свободных колебаний. Когда системе, например, математическому маятнику, придают импульс, чтобы начать движение, дальнейшие его колебания (самостоятельные) будут считаться свободными.