Программа расчета резонансного контура

Резонанс токов

Итак, давайте допустим, мы вогнали наш колебательный контур в резонанс:

Чему будет равняться резонансный ток Iрез ? Считаем по закону Ома:

Iрез = Uген /Rрез , где Rрез = L/CR.

Но самый прикол в том, что у нас при резонансе в контуре появляется свой собственный контурный ток Iкон , который не выходит за пределы контура и остается только в самом контуре! Так как с математикой у меня туго, поэтому я не буду приводить различные математические выкладки с производными и комплексными числами и объяснять откуда берется контурный ток при резонансе. Именно поэтому резонанс параллельного колебательного контура называется резонансом токов.

Применение колебательного контура

Колебательный контур широко применяется на практике. На его основе строятся частотные фильтры, без него не обходится ни один радиоприемник или генератор сигналов определенной частоты.

Если вы не знаете, как подступиться к расчету LC-контура или на это совершенно нет времени, обратитесь в профессиональный студенческий сервис. Качественная и быстрая помощь в решении любых задач не заставит себя ждать!

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Общие сведения

Колебательным контуром называется электрическая цепь, состоящая из конденсатора и катушки индуктивности, применяемой для генерации свободных электромагнитных колебаний в радиоприемниках и радиопередатчиках. Это устройство используется в качестве различных фильтров (полосовых и режекторных). Для подстройки сигналов в сторону увеличения или уменьшения амплитуды используется этот радиоэлемент. Основная функция контура — фильтрация частот.

Широкое распространение устройство получило в военной сфере. В радиолокационных станциях применяются фильтры шумоподавления. Противник использует различные постановщики помех, блокирующие обнаружение цели. В состав техники входит специальное устройство, состоящее из обыкновенных контуров, но с сердечником из специального сплава. Помехи «фильтруются», и оператор радиолокационной станции получает полную картину воздушной обстановки.

Устройство можно применять и для автоматизации. Например, в состав самолетов включен блок для регулировки частоты. Основными его элементами являются два контура, которые настроены только на две частоты — 760 и 840 Гц. На них приходит напряжение с частотой 790 Гц от специального генератора. Последний издает всего 395 Гц. Если частота отклоняется от номинального значения в меньшую сторону, то реактивное сопротивление одного из контуров уменьшается.

После этого активируется электроника блока, и выдается сигнал на увеличение оборотов генератора. Когда величина частоты превышает номинальное значение, реактивное сопротивление другого контура увеличивается. В результате этого срабатывает автоматика, и поступает другой тип сигнала на уменьшение оборотов генератора.

Как работает контур колебаний

Работа контура колебаний основана на циклическом преобразовании энергии индуктивности в качественный показатель эффективности конденсатора и наоборот. Допустим, что конденсатор полностью заряжен и энергия, запасенная в нем, максимальна. При подключении его к катушке индуктивности, он начинает разряжаться. При этом, через индуктивность начинает протекать ток, вызывающий появление ЭДС самоиндукции, направленную на уменьшение протекающего тока. Это означает, что начинается процесс перезарядки конденсатора. В тот момент, когда энергия прибора становится равной нулю, та же величина для катушки максимальна.

Далее, энергия индуктивности снижается, расходуясь на заряд емкости с противоположной полярностью. После уменьшения показателя коэффициента самоиндукции до нуля, на конденсаторе она опять имеет максимальное значение.

Вам это будет интересно Средства защиты от статического электричества

Процессы в системе

Важно! В идеальном случае, данный процесс способен протекать бесконечно. В реальных устройствах колебание затухает со скоростью, пропорциональной потерям в цепи проводников

Вне зависимости от величины энергии, наличия потерь, частота колебаний постоянна и зависит только от значений параметров коэффициента самоиндукции и емкости. Данная величина называется резонансной. Формула резонанса учитывает значение величины емкости и индуктивности контура колебаний.

Осциллограмма

При воздействии на электрическую цепь с катушкой внешним сигналом с частотой, равной резонансной, амплитуда изменения положения частиц резко возрастает. Резонанс отсутствует при несовпадении частот. Из-за предельных значений электрическую цепь с катушкой индуктивности часто называют резонансной.

Потери в цепи с катушкой индуктивности (потери в диэлектрике конденсатора, сопротивление самого устройства, соединительных проводов) ограничивают величину предельных изменений направления частиц. В следствие этого, введена характеристика электроцепи, именуемая добротностью. Добротность обратно пропорциональна предельной величине потерь.

Зависимость предельной частоты от добротности

Важно! Снижение добротности приводит к тому, что предел изменения направлений наступает не только на основной частоте, но и на некотором приближении к ней, то есть, в некоторой полосе частот, где резонансное значение находится посередине. Чем выше добротность, тем более узкой становится полоса частот

2.2. RLC-контур. Свободные колебания window.top.document.title = «2.2. RLC-контур. Свободные колебания»;

В электрических цепях, так же как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания. Простейшей электрической системой, способной совершать свободные колебания, является последовательный RLC-контур (рис. 2.2.1).

Когда ключ K находится в положении 1, конденсатор заряжается до напряжения . После переключения ключа в положение 2 начинается процесс разрядки конденсатора через резистор R и катушку индуктивности L. При определенных условиях этот процесс может иметь колебательный характер.

Закон Ома для замкнутой RLC-цепи, не содержащей внешнего источника тока, записывается в виде

qqtRLC

Рассмотрим сначала случай, когда в контуре нет потерь электромагнитной энергии (R = 0). Тогда

Здесь принято обозначение: Уравнение (*) описывает свободные колебания в LC-контуре в отсутствие затухания. По виду оно в точности совпадает с уравнением свободных колебаний груза на пружине в отсутствие сил трения (ч. I, § 2.2). Рис. 2.2.2 иллюстрирует аналогию процессов свободных электрических и механических колебаний. На рисунке приведены графики изменения заряда q (t) конденсатора и смещения x (t) груза от положения равновесия, а также графики тока J (t) и скорости груза υ (t) за один период колебаний.

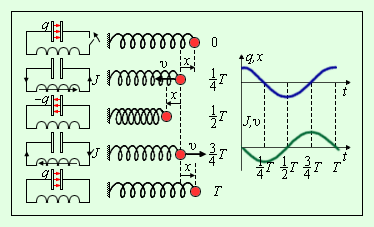Рисунок 2.2.2.Аналогия процессов свободных электрических и механических колебаний

Сравнение свободных колебаний груза на пружине и процессов в электрическом колебательном контуре позволяет сделать заключение об аналогии между электрическими и механическими величинами. Эти аналогии представлены в таблице 1.

В отсутствие затухания свободные колебания в электрическом контуре являются гармоническими, то есть происходят по закону

Параметры L и C колебательного контура определяют только собственную частоту свободных колебаний

Амплитуда q и начальная фаза φ определяются начальными условиями, то есть тем способом, с помощью которого система была выведена из состояния равновесия. В частности, для процесса колебаний, который начнется в контуре (рис. 2.2.1) после переключения ключа K в положение 2, q = C, φ = 0.

При свободных колебаниях происходит периодическое превращение электрической энергии W_э, запасенной в конденсаторе, в магнитную энергию W_м катушки и наоборот. Если в колебательном контуре нет потерь энергии, то полная электромагнитная энергия системы остается неизменной:

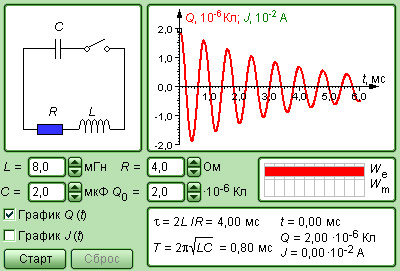
Все реальные контуры содержат электрическое сопротивление R. Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в джоулево тепло, и колебания становятся затухающими (рис. 2.2.3).

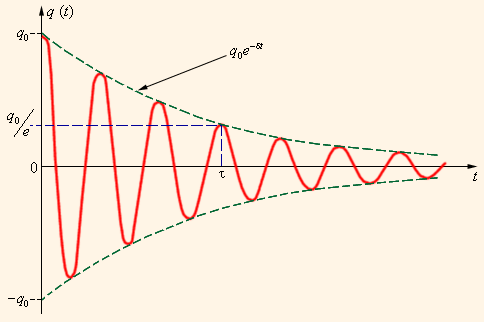Рисунок 2.2.3.Затухающие колебания в контуре

Затухающие колебания в электрическом контуре аналогичны затухающим колебаниям груза на пружине при наличии вязкого трения, когда сила трения изменяется прямо пропорционально скорости тела: F_тр = – βυ. Коэффициент β в этой формуле аналогичен сопротивлению R электрического контура. Уравнение свободных колебаний в контуре при наличии затухания имеет вид

Физическая величина δ = R / 2L называется коэффициентом затухания. Решением этого дифференциального уравнения является функция

exp (–δt)Re ≈ 2,7 разавременем затухания

NQ

Для RLC-контура добротность Q выражается формулой

Добротность электрических контуров, применяемых в радиотехнике, обычно порядка нескольких десятков и даже сотен.

Следует отметить, что собственная частота ω свободных колебаний в контуре с не очень высокой добротностью несколько меньше собственной частоты ω идеального контура с теми же значениями L и C. Но при Q ≥ (5÷10) этим различием можно пренебречь.

Модель. Свободные колебания в RLC-контуре

Формулы расчета последовательного колебательного контура

Здесь будет немного теории колебательного контура с отступлениями и комментариями. Надеюсь, что эта информация будет полезна не только студентам и школьникам, но и поможет радиолюбителям, дополнив практику теорией, может быть забытой кем-то, может для кого-то новой.

Последовательный колебательный контур – это цепь, составленная из последовательно соединенных индуктивности и ёмкости.(рис1) рис 1

R – это эквивалентное («виртуальное») активное сопротивление контура, характеризующее потери в реактивных элементах. При этом сами L и C, можно представить как идеальные без потерь.

È – синусоидальный источник, напряжение которого описывается уравнением È = Èmejωt , где ω– это конечно не число витков катушки, а круговая частота: ω = 2πƒ. Тогда ток в цепи: Ì = È / Ζ, где Ζ – полное комплексное сопротивление цепи, которое, как известно, для последовательной цепи определяется как сумма сопротивлений всех ее элементов

Ζ = R + (jωL + 1 / jωC) = R + jωX

Или, что тоже самое:

Ζ = ¦Ζ¦ejφ, где ¦Ζ¦ = √R2 + X2, φ = arctg(X / R), X = ωL — (1 / ωC)

Активную составляющую входного сопротивления R можно приближенно считать не зависящей от частоты генератора, хотя реально это совсем не так. Здесь работают факторы скин-эффекта, эффекта близости другие эффекты от которых зависит добротность. Но для получения представления как меняется реактивное сопротивление контура от частоты пока этими тонкостями можно пренебречь. Реактивная составляющая является функцией частоты и в зависимости от величины L, C, и ω изменяется по величине и знаку (рис2).

рис 2

В точке ω0 контур попадает в режим, при котором XC= — XL, X=0. Этот режим называется резонансом напряжений, при этом ω0L — 1/ω0C = 0, откуда

ω0 = 1/√LC или ƒ0 = 1/(2π√LC),

формула резонансной частоты контура, впервые выведенная сэром (1824 – 1907), великим английским физиком, более известным как лорд Кельвин, в честь которого названа шкала абсолютных температур.

В точке резонанса Ζ = R. Ток в цепи: Ì0 = È/R, напряжения на емкости и индуктивности равны и противоположны по знаку

UC = UL = ω0LÌ0 = (1/ω0C)Ì0

При этом

UL/Ì0 = UC/Ì0 = ω0L = 1/ω0C = √L/C = ρ

ρ–характеристическое или волновое сопротивление контура.

Очевидно, что ρ » R, поэтому UC = UL » E, откуда и произошло название – резонанс напряжений. Т.е. амплитуда напряжения на реактивных элементах на резонансной частоте в десятки и сотни раз превышает амплитуду напряжения источника. Подобное явление наблюдается в механике, например маятник в часах, качели и носит общее название явление резонанса.

Это возрастание амплитуды характеризуется следующими соотношениями

UL/E = UC/E = ρ/R = Q

Q – безразмерная величина, носящая название добротности контура.

Обратим внимание на выражение Q = ρ/R = √L/C/R, из которого следует, что добротность должна расти при увеличении соотношения L/C. Однако, это не совсем так

Дело в том, что при увеличении L одновременно растет и R, ведь число витков и размеры катушки увеличиваются и, грубо говоря, увеличивается длина провода катушки и его омическое сопротивление. Поэтому зависимость величины добротности контура от соотношения индуктивности и емкости носит более сложный характер и простыми формулами не описывается. В начале мы пренебрегли «тонкостями» зависимости активного сопротивления контура от частоты, но здесь уже так легкомысленно поступать нельзя.

Вообще, конструкция контура для разных областей его применения разрабатывалась в основном энтузиастами радиолюбителями с паяльником в руках, интуицией и минимумом расчетов. Так было на заре развития радио. Тогда в результате экспериментов было установлено, что добиться хорошей чувствительности и избирательности приемника, например, можно применив контур с катушкой внушительных размеров. Потом уже с появлением малошумящих полупроводников и высокочастотных ферритов размеры перестали играть такое значение. Но и сегодня практический опыт нельзя оставлять без внимания, советую ознакомится с ним на этом

Амплитудно-частотая характеристика тока в цепи колебательного контура описывается уравнением:

I/I0 = 1/√1+Q2(ƒ/ƒ0-ƒ0/ƒ)2

Фазочастотная характеристика определяется выражением:

φ = arctg[Q(ƒ/ƒ0-ƒ0/ƒ)]

Эти характеристики относительно нормированной частоты ω/ω0 приведены на следующем рисунке:

Из этих графиков видно, что колебательный контур можно использовать как частотно-избирательную или фазо-сдвигаюшую цепь.

Формула индуктивности

Расчет резонанса колебательного контура производится на основании значений емкости и индуктивности. Как правило, емкость конденсатора является постоянной величиной, за исключением случаев использования переменных устройств в перестраиваемых электроцепях. Коэффициент самоиндукции катушки зависит от многих факторов:

• Количество и расположение витков обмотки;
• Наличие или отсутствие сердечника;
• Материал сердечника.

Общей формулы для определения индуктивности катушки колебательного контура не существует. Для расчетов используют формулы, соответствующие форме катушки. К сожалению, все формулы определения качественной величины электрической цепи с подсоединённой к ней катушкой индуктивности позволяют производить только приблизительные расчеты.

Вам это будет интересно Особенности активно-емкостной нагрузки

Приборы индуктивности различных типов

Важно! Для того, чтобы получить катушку с заданными параметрами, приходится принимать дополнительные меры, например, производить подстройку коэффициента самоиндукции путем изменения длины сердечника или корректировки расстояния между витками в однорядных катушках

Пример решения

Для устройства нужно произвести расчет контура с частотой резонанса 1 МГц. Можно воспользоваться описанными формулами, однако радиолюбители произвели некоторые вычисления и предложили более упрощенный вариант: L = (159,1 / f)^2 / C. Для контура можно взять приближенное значение емкости плоского конденсатора, равное 1000 пкФ. На корпусе указывается этот параметр.

Кроме того, маркировка может содержать напряжение, на которое он рассчитан. Подставив все значения в формулу, можно узнать индуктивность: L = (159,1 / 1)^2 / 1000 = 25 (мкГн). После этого следует вычислить количество витков N катушки с диаметром каркаса D по такому соотношению: N = 32 * ^(½). Если предположить, что D = 5 мм (можно взять со старых контуров), то N = 32 * [25 / 5]^(½) = 72 (витка). Однако за основу можно взять катушку с подстроечным ферритовым сердечником со следующими параметрами:

• длина — 13—15 мм;
• диаметр — 2,3—3,2 мм.

Можно воспользоваться таким соотношением: N = 8,5 * L^(½) = 8,5 * 25^(½) = 43 (витка). Провод следует брать 0,1 мм в диаметре. Это показатель измеряется при помощи штангенциркуля.

Таким образом, колебательный контур является простейшей системой для генерации электромагнитных колебаний, затухание которых зависит от частоты резонанса и добротности радиоэлемента.

Формула индуктивности

Расчет резонанса колебательного контура производится на основании значений емкости и индуктивности. Как правило, емкость конденсатора является постоянной величиной, за исключением случаев использования переменных устройств в перестраиваемых электроцепях. Коэффициент самоиндукции катушки зависит от многих факторов:

• Количество и расположение витков обмотки;
• Наличие или отсутствие сердечника;
• Материал сердечника.

Общей формулы для определения индуктивности катушки колебательного контура не существует. Для расчетов используют формулы, соответствующие форме катушки. К сожалению, все формулы определения качественной величины электрической цепи с подсоединённой к ней катушкой индуктивности позволяют производить только приблизительные расчеты.

Вам это будет интересно Вычисление площади поперечного сечения

Приборы индуктивности различных типов

Важно! Для того, чтобы получить катушку с заданными параметрами, приходится принимать дополнительные меры, например, производить подстройку коэффициента самоиндукции путем изменения длины сердечника или корректировки расстояния между витками в однорядных катушках

Резонанс токов – обзор понятия и методики расчета

Резонанс токов, хорошо известный как естественный токовый «параллельный резонанс» — процесс или явление, которое протекает в условиях параллельного типа колебательного контура и наличия напряжения.

В данном случае частота источника напряжения должна иметь совпадение с аналогичными резонансными показателями контура.

Применение токового резонанса

Основная область активного применения широко востребованных резонансных токов сегодня представлена:

• некоторыми видами фильтрующих систем, в которых току с определенными частотными параметрами оказываются значительные показатели сопротивления;
• радиотехникой в виде приемников, выделяющих сигналы, предназначенные для конкретных точек радиостанций. Оказание значительного сопротивления току сопровождается снижением показателей контурного напряжения при максимальной частоте;
• асинхронного типа двигателями, в особенности функционирующими в условиях неполной нагрузки;
• установками высокоточной электрической сварки;
• колебательными контурами внутри узлов генераторов электронного типа;
• приборами, отличающимися высокочастотной закалкой;
• снижением показателей генераторной нагрузки. При таких условиях в приемном трансформаторе с первичной обмоткой делается колебательный контур.

Схема цепи

Особенно часто колебательные контуры или токовые резонансы применяются в производстве современного промышленного индукционного котлового оборудования, что позволяет в значительной степени улучшить стартовые показатели коэффициента полезного действия.

Стандартные колебательные контуры, функционирующие в условиях режима токового резонанса, массово применяются в качестве одного из наиболее важных узлов в современных электронных генераторах.

Резонанс токов в цепи с переменным током

Протекание тока внутри электрической цепи с последовательным, параллельным или смешанным типом соединения элементов, вызывает получение различных режимов функционирования.

Таким образом, резонанс электрической цепи является режимом участка, который содержит элементы индуктивного и емкостного типа, а угол фазового сдвига между токовыми величинами и показателями напряжения нулевые.

https://youtube.com/watch?v=R4_cYB6m-zI

В соединяемых параллельным способом конденсаторе и катушечной части наблюдается равное реактивное сопротивление, чем обусловлен резонанс.

Также должен учитываться тот факт, что для катушечной части и конденсатора характерно полное отсутствие активного сопротивления, а равенство реактивного сопротивления делает нулевыми общие токовые показатели внутри неразветвленной части электрической цепи и большие величины тока в ветвях.

Операция

Анимированная диаграмма, показывающая работу настроенной цепи (LC-цепи). Конденсатор C накапливает энергию в своем электрическом поле E, а индуктор L накапливает энергию в своем магнитном поле B ( зеленый ) . Анимация показывает схему в прогрессивных точках колебания. Колебания замедляются; в реальной настроенной цепи заряд может колебаться назад и вперед от тысячи до миллиардов раз в секунду.

LC-контур, колеблющийся на своей собственной резонансной частоте , может накапливать электрическую энергию . Смотрите анимацию. Конденсатор накапливает энергию в электрическом поле ( E ) между пластинами, в зависимости от напряжения на нем, а индуктор накапливает энергию в своем магнитном поле ( B ) в зависимости от протекающего через него тока .

Если катушка индуктивности подключена к заряженному конденсатору, напряжение на конденсаторе будет пропускать ток через катушку индуктивности, создавая вокруг нее магнитное поле. Напряжение на конденсаторе падает до нуля, поскольку заряд расходуется текущим током. В этот момент энергия, запасенная в магнитном поле катушки, индуцирует напряжение на катушке, потому что индукторы противодействуют изменениям тока. Это индуцированное напряжение заставляет ток начать перезаряжать конденсатор напряжением, противоположным полярности его первоначального заряда. В связи с законом Фарадея , то ЭДС , который приводит в действие тока обусловлено уменьшением в магнитном поле, таким образом , энергия , необходимая для зарядки конденсатора извлекается из магнитного поля. Когда магнитное поле полностью рассеивается, ток прекращается, и заряд снова сохраняется в конденсаторе с противоположной полярностью, как и раньше. Затем цикл начнется снова, и ток будет течь в обратном направлении через индуктор.

Заряд течет вперед и назад между пластинами конденсатора через катушку индуктивности. Энергия колеблется между конденсатором и катушкой индуктивности до тех пор, пока внутреннее сопротивление (если не восполняется из внешней цепи) не заставит колебания затухнуть. Действие настроенной схемы, математически известной как гармонический осциллятор , похоже на маятник, раскачивающийся взад и вперед, или плеск воды в баке; по этой причине контур также называют контуром резервуара . Собственная частота (то есть частота, с которой он будет колебаться, когда он изолирован от любой другой системы, как описано выше) определяется значениями емкости и индуктивности. В большинстве приложений настроенная схема является частью более крупной схемы, которая применяет к ней переменный ток , вызывая непрерывные колебания. Если частота приложенного тока является собственной резонансной частотой схемы ( собственная частота ниже), произойдет резонанс , и небольшой управляющий ток может вызвать колебательные напряжения и токи большой амплитуды. В типичных настроенных схемах электронного оборудования колебания происходят очень быстро, от тысяч до миллиардов раз в секунду.
ж{\ displaystyle f_ {0} \,}

Эффект резонанса

Ярким примером механического класса резонаторов является пружинный маятник. Профессор из технологического Массачусетского института (в Америке), В

Левин, акцентирует внимание своих студентов на то, что резонанс (resonance) – это эффект, сопряжённый с увеличением амплитуды. Для демонстрации явления используется установка. Она состоит из следующих компонентов:

Она состоит из следующих компонентов:

• электродвигатель;
• механизм, превращающий вращение в возвратно-поступательное движение;
• ЛАТР – лабораторный автотрансформатор;
• медная пружина из проволоки с набором грузиков;
• направляющая для пружины.

Направление колебания пружины – вертикальное. Вращение вала мотора заставляет пружину совершать колебания. С помощью автотрансформатора присутствует возможность регулировать напряжение. Регулировка позволяет варьировать частоту вращения вала и колебаний маятника. При изменении частоты вращения вала амплитуда возвратно-поступательного движения остаётся неизменной.

Перед опытом замеряется удлинение медной пружины под действием грузиков (для оценки резонансной частоты пружины). Изменение скорости вращения вала заставляет амплитуду колебания конца пружины с грузом изменяться. Амплитуда увеличивается и на 1-м герце частоты становится максимальной (

Важно! При дальнейшем увеличении скорости вращения вала амплитуда конца пружины начинает уменьшаться. Это означает, что resonance пройден. Если уменьшать напряжение, а с ним и частоту вращения двигателя, снова можно наблюдать эффект resonance колебания пружины

Если уменьшать напряжение, а с ним и частоту вращения двигателя, снова можно наблюдать эффект resonance колебания пружины.

Добротность пружины Q определяется как отношение амплитуды колебания пружины Aпр к амплитуде колебания вынуждающей силы Aвс. В этом случае Q = Aпр/Aвс = 30/5 = 6, где Aвс = 5.

Похожие записи:

Как пользоваться утюгом: обычным и паровым Как выбрать солнечные батареи для частного дома Распиновка usb: расположение контактов и особенности классификации Провод пв 3 Производство электроэнергии в россии Виды аварийного освещения и какие требования предъявляются