Энергия электрического поля конденсатора

Использование двойного электрического слоя

На протяжении многих десятилетий самой большой емкостью обладали электролитические конденсаторы. В них одной из обкладок являлась металлическая фольга, другой — электролит, а изоляцией между обкладками — окись металла, которой покрыта фольга. У электролитических конденсаторов емкость может достигать сотых долей фарады, что недостаточно для того, чтобы полноценно заменить аккумулятор.

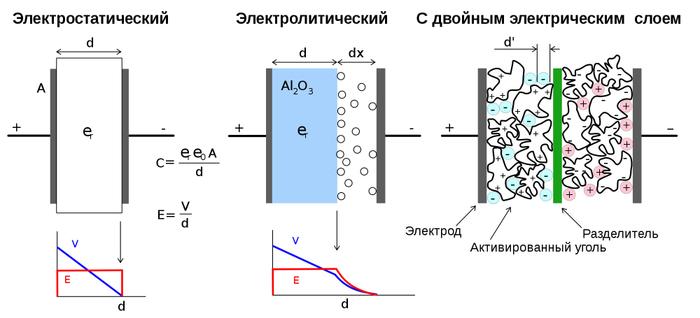
Большую емкость, измеряемую тысячами фарад, позволяют получить конденсаторы, основанные на так называемом двойном электрическом слое. Принцип их работы следующий. Двойной электрический слой возникает при определенных условиях на границе веществ в твердой и жидкой фазах. Образуются два слоя ионов с зарядами противоположного знака, но одинаковой величины. Если очень упростить ситуацию, то образуется конденсатор, «обкладками» которого являются указанные слои ионов, расстояние между которыми равно нескольким атомам.

Суперконденсаторы различной емкости производства Maxwell

Конденсаторы, основанные на данном эффекте, иногда называют ионисторами. На самом деле, этот термин не только к конденсаторам, в которых накапливается электрический заряд, но и к другим устройствам для накопления электроэнергии — с частичным преобразованием электрической энергии в химическую наряду с сохранением электрического заряда (гибридный ионистор), а также для аккумуляторов, основанных на двойном электрическом слое (так называемые псевдоконденсаторы). Поэтому более подходящим является термин «суперконденсаторы». Иногда вместо него используется тождественный ему термин «ультраконденсатор».

Идея суперконденсатора

Несмотря на функциональную схожесть, аккумуляторные батареи и конденсаторы устроены совершенно по-разному. Гальванические элементы работают на принципе высвобождения электрической энергии во время химической реакции веществ внутри них. При истощении запаса активных реагентов они прекращают генерировать разность потенциалов и для нового цикла требуют инициирования током обратных химических реакций для восстановления активных веществ. Основные недостатки аккумуляторов по сравнении и конденсаторами:

непродолжительный жизненный цикл;
невысокая удельная мощность;
узкий диапазон температур зарядки и разрядки;
неспособность быстро отдать весь запас энергии.

Тем не менее обычные конденсаторы не используются в качестве активных источников напряжения из-за низкой ёмкости. Теоретические и практические суперконденсаторы (ультраконденсаторы) отличаются от обычных крайне высокой ёмкостью при большой плотности хранимой энергии, что позволяет их рассматривать как альтернативу химическим элементам.

Первые ультраконденсаторы появились в середине прошлого века и обладали не очень впечатляющими ёмкостями. С тех пор прогресс в совершенствовании материалов привёл к утоньшению диэлектрического слоя до одной молекулы, что позволило создавать устройства с выдающимися характеристиками. Дальнейшее развитие наноиндустрии стало основой для фундаментальных перемен в накоплении электричества. Возможно, в скором времени экологически опасные и капризные химические аккумуляторы заменят суперконденсаторы на основе молекулярно структурированных пластин и диэлектрического слоя.

Резонанс напряжений

Давайте возьмем другие параметры катушки и конденсатора и посмотрим, что у нас происходит на самих радиоэлементах. Нам ведь надо досконально все выяснить ;-). Беру катушку индуктивности с индуктивностью в 22 микрогенри:

и конденсатор в 1000 пФ

Из них собираю последовательный колебательный контур. Итак, чтобы поймать резонанс, я не буду в схему добавлять резистор. Поступлю более хитрее.

Так как мой генератор частоты китайский и маломощный, то при резонансе у нас в цепи остается только активное сопротивление потерь R. В сумме получается все равно маленькое значение сопротивления, поэтому ток при резонансе достигает максимальных значений. В результате этого, на внутреннем сопротивлении генератора частоты падает приличное напряжение и выдаваемая амплитуда частоты генератора падает. Я буду ловить минимальное значение этой амплитуды. Следовательно это и будет резонанс колебательного контура. Перегружать генератор – это не есть хорошо, но что не сделаешь ради науки!

Ну что же, приступим ;-). Давайте сначала посчитаем резонансную частоту по формуле Томсона. Для этого я открываю онлайн калькулятор на просторах интернета и быстренько высчитываю эту частоту. У меня получилось 1,073 Мегагерц.

Ловлю резонанс на генераторе частоты по его минимальным значениям амплитуды. Получилось как-то вот так:

Размах амплитуды 4 Вольта

Хотя на генераторе частоты размах более 17 Вольт! Вот так вот сильно просело напряжение. И как видите, резонансная частота получилась чуток другая, чем расчетная: 1,109 Мегагерц.

Теперь небольшой прикол

Вот этот сигнал мы подаем на наш последовательный колебательный контур:

Как видите, мой генератор не в силах выдать большую силу тока в колебательный контур на резонансной частоте, поэтому сигнал получился даже чуть искаженным на пиках.

Ну а теперь самое интересное. Давайте замеряем падение напряжения на конденсаторе и катушке на резонансной частоте. То есть это будет выглядеть вот так:

Смотрим напряжение на конденсаторе:

Размах амплитуды 20 Вольт (5х4)! Откуда? Ведь подавали мы на колебательный контур синус с частотой в 2 Вольта!

Ладно, может с осциллографом что-то произошло?. Давайте замеряем напряжение на катушке:

Народ! Халява!!! Подали 2 Вольта с генератора, а получили 20 Вольт и на катушке и на конденсаторе! Выигрыш энергии в 10 раз! Успевай только снимать энергию с конденсатора или с катушки!

Ну ладно раз такое дело… беру лампочку от мопеда на 12 Вольт и цепляю ее к конденсатору или катушке. Лампочке ведь вроде как по-барабану на какой частоте работать и какой ток кушать. Выставляю амплитуду, чтобы на катушке или конденсаторе было где то Вольт 20 так как среднеквадратичное напряжение будет где-то Вольт 14, и цепляю поочередно к ним лампочку:

Как видите – полный ноль. Лампочка гореть не собирается, так что побрейтесь фанаты халявной энергии). Вы ведь не забыли, что мощность определяется произведением силы тока на напряжение? Напряжения вроде как-бы хватает, а вот силы тока – увы! Поэтому, последовательный колебательный контур носит также название узкополосного (резонансного) усилителя напряжения, а не мощности!

Объяснение резонанса напряжения

При резонансе напряжение на катушке и на конденсаторе оказались намного больше, чем то, которое мы подавали на колебательный контур. В данном случае у нас получилось в 10 раз больше. Почему же напряжение на катушке при резонансе равняется напряжению на конденсаторе. Это легко объясняется. Так как в последовательном колебательном контуре катушка и кондер идут друг за другом, следовательно, в цепи протекает одна и та же сила тока.

При резонансе реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора. Получаем по правилу шунта, что на катушке у нас падает напряжение UL = IXL , а на конденсаторе UC = IXC . А так как при резонансе у нас XL = XC , то получаем что UL = UC , ток ведь в цепи один и тот же ;-). Поэтому резонанс в последовательном колебательном контуре называют также резонансом напряжений, так как напряжение на катушке на резонансной частоте равняется напряжению на конденсаторе.

Конденсаторы

Для практического использования электрической энергии необходимо уметь ее накапливать. Для этого используют специальные устройства — конденсаторы.

Конденсаторы — это устройства, которые состоят из двух или более проводников, разделенных тонким слоем диэлектрика.

Проводники, из которых состоит конденсатор, называются обкладками

Как правило, при зарядке конденсатора заряды его обкладок равны по величине и противоположны по знаку. Под зарядом конденсатора

понимают значение заряда положительно заряженной обкладки.

Термин «конденсатор » от латинского слова condensare — сгущать ввел А.Вольта (итальянский физик) в 1782 г. Первые электрические конденсаторы были изготовлены Э.Клейстом и П. Ван Мушенбреком в 1745 г. По имени города Лейдена, где работал Мушенбрек, французкий физик Жан Нолле назвал их лейденскими банками.

При небольших размерах конденсатор отличается значительной емкостью, не зависящей от наличия вблизи него других зарядов или проводников.

Электроемкостью конденсатора называют физическую величину, численно равную отношению заряда конденсатора к разности потенциалов между его обкладками:

\(~C = \dfrac{q}{\varphi_1 — \varphi_2}\) или \(~C = \dfrac qU .\)

Из этой формулы видно, что чем больше напряжение между обкладками конденсатора, тем больше на них заряд. Но для каждого конденсатора существует предельное (максимальное)напряжение , выше которого диэлектрик начнет разрушаться. При этом заряды обкладок конденсатора мгновенно нейтрализуются, происходитпробой , т.е. конденсатор выходит из строя.

Виды конденсаторов

Конденсаторы можно классифицировать по следующим признакам и свойствам:

по форме обкладок различают конденсаторы плоские, сферические, цилиндрические и др.;
по типу диэлектрика (рис. 1) —бумажные (а), воздушные (б), слюдяные, керамические, электролитические (в) и т.д.;
по рабочему напряжению — низковольтные (напряжение пробоя до 100 В) и высоковольтные (выше 100 В);
по возможности изменения своей емкости — постоянной емкости (см. рис. 1, а, в), переменной емкости (см. рис. 1, б), подстроечные (рис. 2).

Рис. 1

Рис. 2
Рис. 3

Другие виды конденсаторов показаны на рисунке 3.

См. так же Wikipedia Классификация конденсаторов

Электроемкость плоского конденсатора C

зависит от площади обкладокS , расстояния между нимиd и диэлектрической проницаемости диэлектрика ε, заполняющего пространство между обкладками конденсатора, но не зависит от материала, из которого эти пластины изготовлены \(~C = \dfrac{\varepsilon_0 \cdot \varepsilon \cdot S}{d},\) где ε0 — электрическая постоянная.

*Вывод формулы

Поле плоского конденсатора можно рассматривать как совокупность полей двух бесконечных разноименно заряженных плоскостей (рис. 2, а и б). Напряженность поля (рис. 2, в) можно найти по принципу суперпозиции:

\(\vec{E}=\vec{E}_{1} +\vec{E}_{2},\)

где \( E_{1} = E_{2} =\dfrac{\sigma }{2\varepsilon _{0} \cdot \varepsilon } =\dfrac{q}{2\varepsilon _{0} \cdot \varepsilon \cdot S}\) — напряженности электрических полей каждой из обкладок конденсатора, σ

— поверхностная плотность заряда на обкладках конденсатора. Тогда в проекциях на ось 0Х:

справа и слева от пластин — \(E_х = 0\);

между пластин — \(E=2E_{1} =\dfrac{q}{\varepsilon _{0} \cdot \varepsilon \cdot S}.\)

Рис. 4 Электроемкость плоского конденсатора \(~C = \dfrac qU\), где \(U = E \cdot d,\) d

— расстояние между пластин. Следовательно, \(C =\dfrac{q}{E\cdot d} = \dfrac{q}{d} \cdot \dfrac{1}{E} = \dfrac{q}{d} \cdot \dfrac{\varepsilon _{0} \cdot \varepsilon \cdot S}{q} = \dfrac{\varepsilon _{0} \cdot \varepsilon \cdot S}{d}.\).

При быстром разряде конденсатора можно получить импульс большой мощности, например, в фотовспышках, электромагнитных ускорителях, импульсных лазерах и т. п.
Так как конденсатор способен длительное время сохранять заряд, то его можно использовать в качестве элемента памяти или устройства хранения электрической энергии.
Емкость конденсатора заметно изменяется при малейших изменениях параметра конденсатора. Так малое изменение расстояния между обкладками учитывается в измерителях малых перемещений, изменение состава диэлектрика при изменении влажности фиксируется в измерителях влажности, учет изменения высоты диэлектрика между обкладками конденсатора позволяет измерять уровень жидкости и т.п.
Конденсаторы (совместно с катушками индуктивности и/или резисторами) используются для построения различных цепей с частотно-зависимыми свойствами, в частности, фильтров, цепей обратной связи, колебательных контуров и т. п.

Формула электроемкости конденсатора

Обкладки должны иметь такую форму и быть расположены так относительно друг друга, что поле, которое создается данной системой, было максимально сосредоточено в ограниченной области пространства, между обкладками.

Назначение конденсатора в том, чтобы накапливать и отдавать в электрической цепи заряд.

Основной характеристикой конденсатора является электрическая емкость (C). Электрическая емкость конденсатора – это взаимная емкость принадлежащих ему обкладок:

q – величина заряда на обкладке; – разность потенциалов между обкладками.

Электрическая ёмкость конденсатора зависит от диэлектрической проницаемости диэлектрика, который заполняет пространство между его обкладками. Если пространство между обкладками одного конденсатора заполнено диэлектриком с проницаемостью равной , а у второго конденсатора воздух между пластинами, то емкость конденсатора с диэлектриком (C) в раз больше, чем емкость воздушного конденсатора ():

Формула электроемкости основных типов конденсаторов

При расчете электроемкости плоского конденсатора нарушением однородности поля около краёв обкладок обычно пренебрегают. Это становится возможным, если расстояние между пластинами существенно меньше, чем линейные размеры обкладок. В таком случае электрическую емкость плоского конденсатора вычисляют при помощи формулы:

где – электрическая постоянная; S – площадь каждой (или наименьшей) пластины; d – расстояние между пластинами.

Если плоский конденсатор между обкладками имеет N слоев диэлектрика, при этом толщина каждого слоя равна , а диэлектрическая проницаемость , то его электрическую емкость рассчитывают при помощи формулы:

Цилиндрический конденсатор составляют две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполнено диэлектриком. При этом емкость цилиндрического конденсатора находят как:

где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.

У сферического конденсатора обкладками служат две концентрические сферические проводящие поверхности, пространство обкладками заполняет диэлектрик. Емкость сферического конденсатора вычисляют как:

где – радиусы обкладок конденсатора. Если , то можно считать, что , тогда, мы имеем:

так как – площадь поверхности сферы, и если обозначить , то получим формулу для емкости плоского конденсатора (3). Если расстояние между обкладками сферического и цилиндрического конденсаторов малы (в сравнении с их радиусами), то в приближенных расчетах используют формулу емкости для плоского конденсатора.

Электрическую емкость для линии из двух проводов находят как:

где d – расстояние между осями проводов; R – радиус проводов; l – длина линии.

Формулы для вычисления электрической емкости соединений конденсаторов

Если конденсаторы соединены параллельно, то суммарная емкость батареи (C) находится как сумма емкостей отдельных конденсаторов ():

При последовательном соединении конденсаторов емкость батареи вычисляют как:

Если последовательно соединены N конденсаторов, с емкостями то емкость батареи найдем как:

Сопротивление конденсатора

Если конденсатор включен в цепь с постоянного тока, то сопротивление конденсатора можно считать бесконечно большим.

При включении конденсатора в цепь переменного тока, его сопротивление носит название емкостного, и вычисляют его с помощью формулы:

где – частота переменного тока; – угловая частота тока; C – емкость конденсатора.

Энергия поля конденсатора

Электрическое поле локализованное между пластинами конденсатора обладает энергией, которую можно вычислить при помощи формулы:

где –энергия поля конденсатора; q – заряд конденсатора; C – емкость конденсатора; – разность потенциалов между обкладками конденсатора.

Энергия поля плоского конденсатора:

Практические измерения

Значение ёмкости конденсатора обозначается на корпусе в дробных фарадах или с помощью цветового кода. Но со временем компоненты способны потерять свои качества, поэтому для некоторых критических случаев последствия могут быть неприемлемыми. Существуют и другие обстоятельства, требующие измерений. Например, необходимость знать общую ёмкость цепи или части электрооборудования. Приборов, осуществляющих непосредственное считывание ёмкости, не существует, но значение может быть вычислено вручную или интегрированными в измерительные устройства процессорами.

Для обнаружения фактической ёмкости нередко используют осциллограф как средство измерения постоянной времени (т). Эта величина обозначает время в секундах, за которое конденсатор заряжается на 63%, и равна произведению сопротивления цепи в омах на ёмкость цепи в фарадах: т=RC. Осциллограф позволяет легко определить постоянную времени и даёт возможность с помощью расчётов найти искомую ёмкость.

Существует также немало моделей любительского и профессионального электронного измерительного оборудования, оснащённого функциями для тестирования конденсаторов. Многие цифровые мультиметры обладают возможностью определять ёмкость. Эти устройства способны контролируемо заряжать и разряжать конденсатор известным током и, анализируя нарастание результирующего напряжения, выдавать довольно точный результат. Единственный недостаток большинства таких приборов — сравнительно узкий диапазон измеряемых величин.

Вам это будет интересно Цифровой прибор мультиметр и измерение мультитестером

https://www.youtube.com/watch?v=8TpQzXyb9u4

Энергия устройства

Зарядить конденсатор мгновенно невозможно. Для этого процесса требуется определённое время. Это явление используется в радиотехнике. Так, с помощью конденсатора сглаживаются импульсные всплески. В первом приближении конденсатор похож на аккумулятор. Но при этом он отличается от него принципом накопления энергии, ёмкостью и скоростью заряда разряда. При подключении источника питания к выводам обкладок устройства конденсатор накапливает на них заряд.~

Работу устройства можно объяснить по аналогии с протеканием воды. Пусть имеется сосуд с жидкостью площадью поперечного сечения S. По сути, это эквивалент ёмкости. Тогда вода это будет заряд, а высота водяного столба — напряжение. Получается, что энергия — это произведение зарядов на высоту. Но если аккумулятор можно представить как сосуд, в котором имеется тонкий шланг (вывод) и по которому вытекает вода (заряд), то в конденсаторе его диаметр трубки будет равен размеру всей банки. То есть устройство может мгновенно отдать весь накопленный заряд.

При подаче напряжения на обкладки происходит электризация диэлектрика. В результате происходит смещение и на пластины передаётся энергия. На одной из них возникнет избыток электронов, и она условно зарядится отрицательно, а на второй недостаток — проводник станет положительным. Поэтому в формуле, определяющей заряд на обкладках конденсатора, большое значение имеет диэлектрическая проницаемость непроводящего ток вещества.

Между обкладками возникает сила. Величина действующей со стороны первой равняется F = ε1 * q, а со стороны второй F = ε2 * q. Таким образом, можно записать: F = ε1 * q = ε2 * q = E / 2 * q. При увеличении расстояние между обкладками от нулевого до d, будет выполняться работа: A = F * d. Она направлена на преодоление силы взаимодействия между заряженными проводниками.

То есть: A = E / 2 * q * d. Исходя из того, что ε = U/d будет верно записать: А = 1 / 2 q * U. Значит, механическая работа A в соответствии с законом сохранения энергии будет равна количеству зарядов, запасённых в электрическом поле конденсатора: Wэ = C * U2 / 2.

Следует отметить, что при подаче переменного сигнала внутри диэлектрика происходит постоянная смена знаков заряда. В итоге происходит нагревание, что приводит конденсатор к выходу из строя. Характеризуется это явление тангенсом угла диэлектрических потерь. Определяется он как отношение затраченной мощности к реактивной.

Характеристики конденсатора

Основной характеристикой данного элемента является емкость, или С. Она определяет способность устройства собирать электрический заряд, зависит от геометрической конфигурации крышек и от электрической проницаемости диэлектрика между крышками.

Важно! Емкость зависит от типа используемого диэлектрика, а также от геометрических размеров элемента. Для того, чтобы описать принцип работы устройства формулой, необходимо понять, что это постоянная пропорциональность в уравнении, представляющая собой взаимную зависимость накопленного заряда q от площади пластинок и от разности потенциалов V между ними

Для того, чтобы описать принцип работы устройства формулой, необходимо понять, что это постоянная пропорциональность в уравнении, представляющая собой взаимную зависимость накопленного заряда q от площади пластинок и от разности потенциалов V между ними.

Вам это будет интересно Особенности проекта электроснабжения

Мощность выражается в единицах, называемых фарадами F. Но на практике используются и более мелкие единицы, такие как микрофарады и пикофарады.

Внешний вид устройств

Таким образом, если напряжение U приложено к конденсатору, электрический заряд накапливается на крышках детали. Значение накопленного заряда на каждой пластинке одинаково, они отличаются только знаком. Этот процесс накопления электрического показателя на называется зарядкой.

Другим параметром детали является номинальное напряжение, а именно, его максимальное значение, которое может подаваться на конденсатор. При подключении более высокого напряжения возникает пробой диэлектрика. Это приводит к короткому замыканию элемента. Каким будет номинальное значение напряжения, зависит от типа диэлектрика и его толщины.

Важно! Чем толще диэлектрик, тем выше номинальное напряжение, которое он выдерживает. Условные обозначения

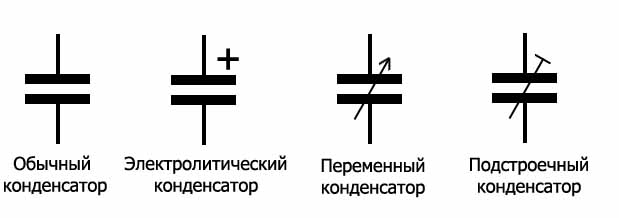
Условные обозначения

Ещё одним параметром является ток утечки -значение проводящего показателя, возникающее при подаче постоянного напряжения на концы элемента.

«Катушка ниток»

Катушка индуктивности представляет собой намотанную изолированную медную проволоку на твердое основание. Что касается изоляции, то выбор материала широк – это и лак, и проводная изоляция, и ткань. Величина магнитного потока зависит от площади цилиндра. Если увеличить ток в катушке, то магнитное поле будет становиться все больше и наоборот.

Если подать электрический ток на катушку, то в ней возникнет напряжение, противоположное напряжению тока, но оно внезапно исчезает. Такого рода напряжение называется электродвижущей силой самоиндукции. В момент включения напряжения на катушку сила тока меняет свое значение от 0 до некоего числа. Напряжение в этот момент тоже меняет значение, согласно закону Ома:

I = U : R,

где I характеризует силу тока, U – показывает напряжение, R – сопротивление катушки.

Еще одной особенной чертой катушки является следующий факт: если разомкнуть цепь «катушка – источник тока», то ЭДС добавится к напряжению. Ток тоже вначале вырастет, а потом пойдет на спад. Отсюда вытекает первый закон коммутации, в котором говорится, что сила тока в катушке индуктивности мгновенно не меняется.

Катушку можно разделить на два вида:

С магнитным наконечником. В роли материала сердца выступают ферриты и железо. Сердечники служат для повышения индуктивности.
С немагнитным. Используются в случаях, когда индуктивность не больше пяти миллиГенри.

Устройства различаются и по внешнему виду, и внутреннему строению. В зависимости от таких параметров находится индуктивность катушки. Формула в каждом случае разная. Например, для однослойной катушки индуктивность будет равна:

L = 10µ0ΠN2R2 : 9R + 10l.

А вот уже для многослойной другая формула:

L= µ0N2R2 :2Π(6R + 9l + 10w).

Основные выводы, связанные с работой катушек:

На цилиндрическом феррите самая большая индуктивность возникает в середине.
Для получения максимальной индуктивности необходимо близко наматывать витки на катушку.
Индуктивность тем меньше, чем меньше количество витков.
В тороидальном сердечнике расстояние между витками не играет роли катушки.
Значение индуктивности зависит от «витков в квадрате».
Если последовательно соединить индуктивности, то их общее значение равно сумме индуктивностей.
При параллельном соединении нужно следить, чтобы индуктивности были разнесены на плате. В противном случае их показания будут неправильными за счет взаимного влияния магнитных полей.

Калькулятор расчета запасаемой энергии в конденсаторе

Конструктивно конденсатор представляет собой емкостной элемент, состоящий из двух параллельно расположенных пластин, пространство между которыми заполнено диэлектриком.

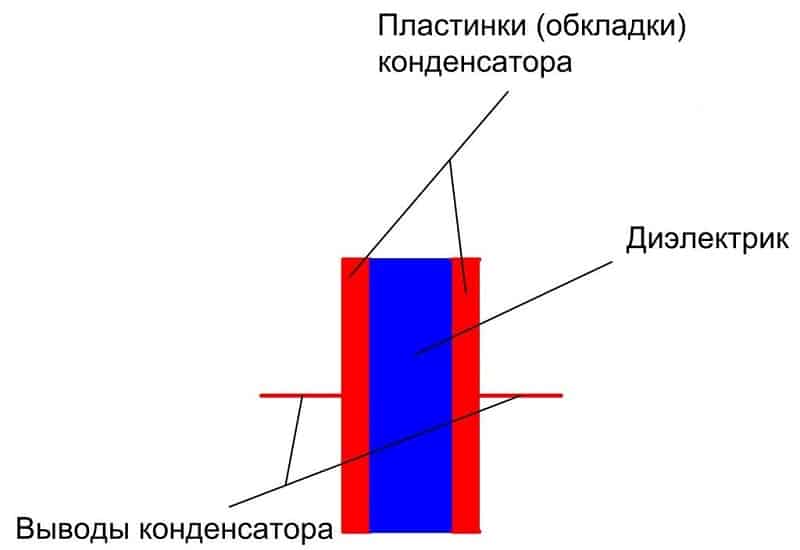
Устройство конденсатора

Принцип работы конденсатора заключается в способности накапливать определенную величину заряда на пластинах и отдавать их обратно в сеть при прохождении через него переменного тока. Для цепи постоянного тока конденсатор представляет собой разрыв, но пластины все равно способны накапливать заряд. Основным параметром конденсатора является емкость, выражающаяся в Фарадах и способность накапливать заряд, выражаемая величиной энергии в Джоулях.

Если емкость конденсатора указывается на корпусе элемента и является его паспортным значением, то количество запасаемой энергии можно определить путем вычислений. Наиболее простым способом вычисления является использования онлайн калькулятора.

Для этого выполните такую последовательность действий:

Внесите в первую графу калькулятора значение напряжения на конденсаторе в Вольтах;
Укажите во втором поле величину емкости элемента в микрофарадах;
Внесите значения сопротивления конденсатора и нажмите кнопку «Рассчитать».

В результате онлайн калькулятор расчета запасаемой энергии в конденсаторе выдаст значение заряда и времени, расходуемого на полный заряд емкостного элемента, подключенного к цепи.

Расчет величины заряда, накапливаемого в конденсаторе, и времени, необходимого для накопления этого заряда производится по таким формулам:

W – это количество запасаемой энергии в конденсаторе;
U – величина напряжения, приложенного к конденсатору;
C – емкость конденсатора.

Для определения времени, затрачиваемого на накопление этого количества запасаемой энергии, в калькуляторе используется формула: Tзар = R*C

Tзар — период времени, необходимый для накопления заряда, зависящий от параметров элемента;
R – величина омического сопротивления конденсатора;
C – емкость конденсатора.

Источник

Расчет конденсатора для светодиодов

Необходимость подключить светодиод к сети – частая ситуация. Это и индикатор включения приборов, и выключатель с подсветкой, и даже диодная лампа.

Существует множество схем подключения маломощных индикаторных LED через резисторный ограничитель тока, но такая схема подключения имеет определённые недостатки. При необходимости подключить диод, с номинальным током 100-150мА, потребуется очень мощный резистор, размеры которого будут значительно больше самого диода.

Вот так бы выглядела схема подключения настольной светодиодной лампы. А мощные десяти ваттные резисторы при низкой температуре в помещении можно было бы использовать в качестве дополнительного источника отопления.

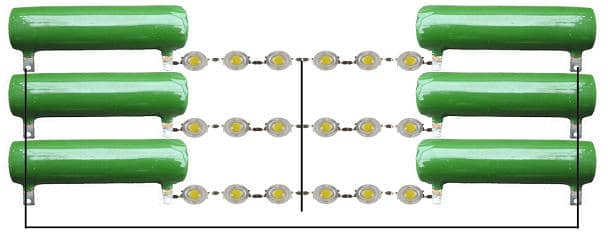
Применение в качестве ограничителя тока конде-ров позволяет значительно уменьшить габариты такой схемы. Так выглядит блок питания диодной лампы мощностью 10-15 Вт.