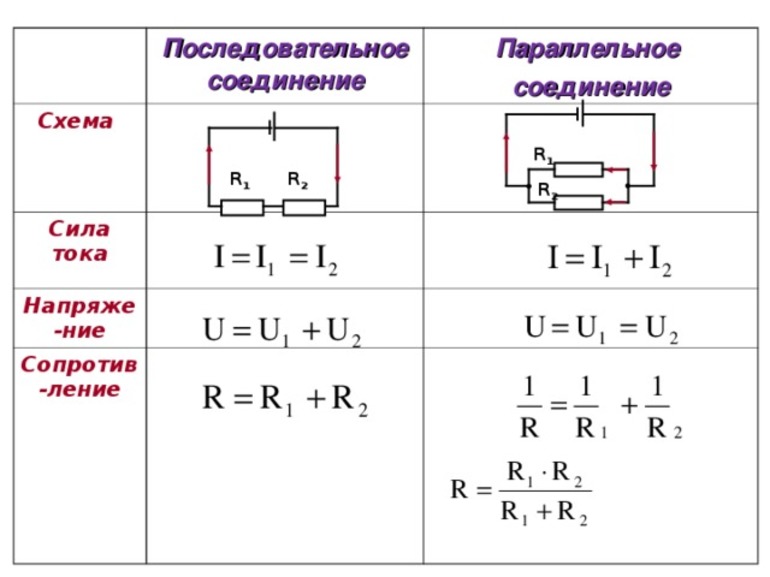
Разница между последовательным и параллельным соединением, преимущества и недостатки
Принципиальные отличия между последовательным и параллельным соединение проводников по ключевым электротехническим параметрам приведены в таблице:
| Параметр/тип соединения | Последовательное | Параллельное |
| Электросопротивление | Равняется сумме электросопротивлений всех электропотребителей. | Меньше значения электросопротивления каждого отдельного из подключенных электроприборов. |
| Напряжение | Равняется совокупному вольтажу всех электропотребителей. | Одинаковая величина на всех участках электроцепи. |
| Сила тока | Одинаковая величина на всех участках электроцепи. | Равняется совокупному значению токов на каждом из приборов. |
За счет своих особенностей каждый из типов сборки цепей имеет свои преимущества и недостатки. Это позволяет использовать данные способы для решения разных электротехнических задач.
Плюсы и минусы последовательного соединения
Основными преимуществам электроцепей из последовательно соединенных приборов являются их следующие особенности:
- простота проектирования и построения схемы;
- низкая стоимость комплектации;
- возможность подключения приборов, рассчитанных на меньшее рабочее напряжение, по сравнению с номинальным напряжением сети;
- выполнение функции регулирования тока – обеспечивает равномерные нагрузки на все приборы.
Однако у этого способа компоновки электросхемы есть и серьезные недостатки. Главным из них является ненадежность цепи из последовательно соединенных проводников. При выходе из строя любого из подключенных приборов, происходит отключение всей цепи.
Кроме того, минусом является снижение напряжения при увеличении количества подключенных потребителей. Примером может служить последовательное соединение нескольких ламп. Чем больше осветительных приборов подключено таким способом к источнику электропитания, тем менее яркий свет они будут давать.
Плюсы и минусы параллельного соединения
При использовании параллельного соединения проводников обеспечиваются такой набор преимуществ:
- стабильность напряжения на электроприборах, вне зависимости от их числа;
- возможность включения или отключения отдельных участков в нужный момент без нарушения работы всей электроцепи;
- надежность – при выходе одного или нескольких компонентов из строя сама электроцепь продолжает сохранять работоспособность.
Недостатком является более сложный расчет и сложная схема, использование которой повышает стоимость комплектации электросети.
Не допускается подключение приборов, с номинальным рабочим вольтажом меньше сетевого. Параллельное соединение аккумуляторов с разным значением вольтажа связано с перетеканием тока в АКБ с меньшей его величиной, что может вызывать ускоренный износ батареи.
Общие сведения
Направленное движение носителей зарядов называют электротоком. Для того чтобы он появился, необходим источник электродвижущей силы — энергии. Но внести материал под действие внешней силы оказывается недостаточно. Например, металлы отлично проводят электрический ток, а вот пластмассы — нет.

Любое физическое тело состоит из электронов и атомов. В свою очередь, последние образуются с помощью протонов и нейтронов. Условно считается, что электрон обладает отрицательным зарядом, а атом — положительным. При этом минусовая частичка вращается по орбитали и удерживается с помощью сил межатомного взаимодействия. Так называемое ядро в целом нейтральное из-за того, что количество отрицательно заряженных частиц совпадает с числом положительных протонов.
Но в некоторых материалах существуют электроны, которые не привязаны к атомам. Называют их свободными. Именно их количество определяет способность к проводимости того или иного вещества. При приложении электромагнитного поля свободные носители начинают движение в одну сторону. Тем самым изменяется потенциальная энергия, начинает течь ток.
Все вещества в физике разделяют на три больших класса:
- диэлектрики — материалы, не проводящие электроток;
- полупроводники — вещества, в которых проводимость появляется только при создании определённых дополнительных условий;
- проводники — физические тела, обладающие большим количеством свободных электронов и из-за этого хорошо проводящие электрический ток.
Характеристикой обратной проводимости является электрическое сопротивление. Эта величина определяет способность проводника препятствовать прохождению тока. Кроме этого, есть и радиодеталь, называемая резистором. Её используют специально для введения в электроцепь активного сопротивления.
https://youtube.com/watch?v=0hFWeR8ybxs
Сопротивление при последовательном и параллельном соединении проводников
Рассмотрим участок цепи AB, представляющий собой последовательное соединение двух резисторов с сопротивлениями R1 и R2.
В соответствии с законом Ома полное сопротивление рассматриваемого участка U = IR, где U — общее напряжение на участке цепи АВ, равное сумме напряжений на каждом из резисторов: U = U1 + U2.
I — сила тока на участке цепи АВ. Она одинакова на всём участке и равна силе тока I1 и I2 в каждом из резисторов. Поэтому можно записать:IR = IR1 + IR2,
IR = I(R1 + R2).
Следовательно, R = R1 + R2.
Общее сопротивление цепи при последовательном соединении равно сумме сопротивлений отдельных проводников.
https://youtube.com/watch?v=1n55v8UTq0g
При последовательном соединении нескольких проводников общее сопротивление цепи равно сумме сопротивлений отдельных проводников: R = R1 + R2 + … Rn.
Способ последовательного подключения всё новых участков цепи реализован в работе реостата, о котором говорилось на предыдущих уроках. Передвигая ползунок реостата, мы увеличиваем или уменьшаем число витков проволоки, включённых последовательно в цепь. При этом сопротивление цепи соответственно увеличивается или уменьшается.
При последовательном соединении проводников их общая длина увеличивается. Поэтому сопротивление цепи становится больше сопротивления любого из проводников.
https://youtube.com/watch?v=Y6ye7dCNGgY
СОПРОТИВЛЕНИЕ ПРИ ПАРАЛЛЕЛЬНОМ СОЕДИНЕНИИ
Рассмотрим участок цепи CD, представляющий собой параллельное соединение двух резисторов с сопротивлениями R1 и R2.
В соответствии с законом Ома I = U/R, где R — общее сопротивление рассматриваемого участка цепи; U — общее напряжение на участке цепи CD, равное напряжениям U1 и U2 на каждом из резисторов; I — сила тока на участке цепи CD, она равна сумме токов в каждом из резисторов: I = I1 + I2.
Поэтому можно записать:
где R1 и R2 — сопротивления первого и второго резисторов соответственно.
Учитывая, что U = U1 = U2, получаем
Следовательно,
Для рассмотренного случая двух резисторов, соединённых параллельно, общее сопротивление цепи можно вычислить по формуле
Таким образом, общее сопротивление цепи при параллельном соединении нескольких резисторов можно вычислить из формулы
Уменьшение общего сопротивления проводников при их параллельном соединении объясняется тем, что общая площадь поперечного сечения проводников на данном участке цепи увеличивается.
https://youtube.com/watch?v=3ZpU_O0htLE
В используемых на практике электрических цепях часто встречается смешанное соединение проводников, включающее в себя как последовательные, так и параллельные участки. При расчёте таких цепей сначала вычисляют необходимые величины на каждом из участков цепи, а затем находят её общие параметры.
Вы смотрели Конспект по физике для 8 класса «Сопротивление при последовательном и параллельном соединении проводников».
Вернуться к Списку конспектов по физике (Оглавление).
Просмотров:
3 633
Область применения
А можно ли на практике использовать данные сведения? Есть ли от них реальная польза?
Прежде всего, рассмотрим организацию соединения проводников и сопротивлений в домашних условиях. Как правило, такие схемы собираются доля обеспечения работы многорожковых люстр, светильников с некоторым количеством ламп освещения. Если использовать здесь последовательную схему, то все лампочки будут включаться одновременно. При использовании параллельного метода можно выводить необходимое количество светильников на один выключатель и включать одну, две и более лампочек в зависимости от ранее принятого решения, с учетом вопросов экономичности, целесообразности и, конечно же, дизайна.
Особенности применения
Каждый из методов подключения нагрузки нашел свое применение в быту и промышленности. Параллельный способ целесообразно использовать в ситуации, когда электроприбор требуется целенаправленно отключать. Примером здесь может стать электрический звонок, соединенный последовательно с источником питания и кнопкой. В соответствии с этим же принципом работает и ручной фонарик, состоящий из светодиода, ключа и батарейки.
Однако последовательное включение приборов не всегда позволяет решить поставленные задачи. В каждой квартире присутствует большое количество осветительных приборов. Если все их соединить последовательно, то они будут включаться и отключаться одновременно, что требуется крайне редко. Именно люстры принято подключать параллельно. В результате у потребителя появится возможность активировать нужное в данный момент количество ламп. Благодаря этому, достигается требуемая освещенность помещения и экономится электрическая энергия.
В быту чаще всего используется смешенное подключение нагрузок. Этот вид подсоединения проводников является сочетанием параллельного и последовательного соединения
При этом на стадии проектирования электросети крайне важно учитывать все преимущества и недостатки каждого типа подсоединения. Для определения необходимых показателей общую цепь следует разделить на простые участки, а полученные результаты затем суммируются.
Что такое конденсатор
Эта деталь содержит две металлических пластины, между которыми находится слой диэлектрика. Когда к пластинам подключают напряжение, на них накапливается заряд. Электрическое находится внутри конденсатора. Оно тем сильнее, чем больший заряд находится на пластинах.
Если отсоединить напряжение от пластин, то конденсатор начинает отдавать заряд. Если используется переменный ток, то полярность напряжения будет периодически меняться. При этом на пластинах будет попеременно то положительный, то отрицательный заряд.
Ёмкость конденсатора является его важнейшей характеристикой. Она характеризует то, сколько энергии он способен пропустить через себя. Её измеряют в фарадах. Поскольку речь идёт об очень большой величине, обычно применяются приставки, которые обозначают, насколько небольшая часть используется. Чаще всего используются микрофарады (такая единицы равны 0,000001 фарады).
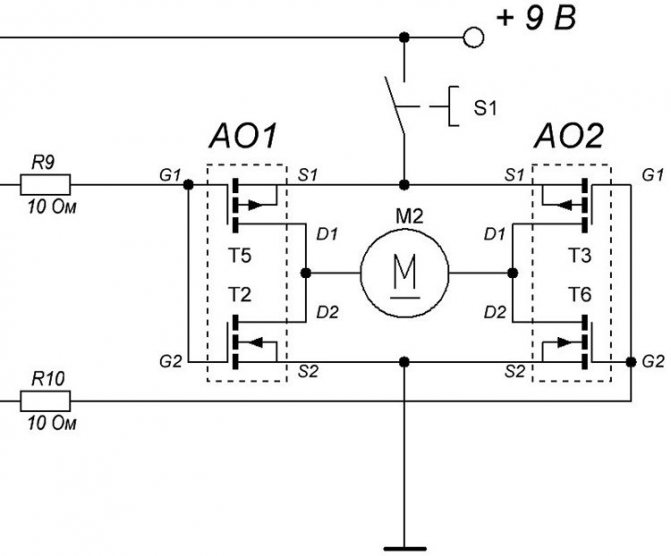
Процедура подключения мотораИсточник kabel-house.ru
Для каждого конденсатора существует номинальное напряжение. При нём эта деталь способна долго и надёжно работать. Обязательно указывается предельная величина наработки, которая выражается в количестве часов.
Существуют различные типы конденсаторов:
Полярные рассчитаны на использование в цепях постоянного тока
Важной особенностью является необходимость подключения в соответствии с указанной на них полярностью. Они обычно имеют небольшие размеры и относительно большую ёмкость.
Неполярные могут подключаться независимо от полярности
Их используют в цепях переменного тока. У них размеры больше, чем у полярных.
Электролитические. В них в качестве пластин используются листы фольги, а диэлектриком является тонкий слой окисла.
Для использования в качестве пускового конденсатора лучше всего подходят электролитические. Их часто используют при частоте переменного тока 50 Гц и напряжении 220-600 вольт. Конденсаторы могут иметь достаточно высокую ёмкость она может составлять сотни тысяч микрофарад.
Эти детали имеют высокую уязвимость к действию перегрева. При нарушении теплового режима они быстро выходят из строя. Неполярные конденсаторы не имеют этого недостатка, однако стоят в несколько раз дороже.
Однофазный асинхронный двигательИсточник asutpp.ru
При параллельном подключении ёмкости складываются. В том случае, когда её не хватает, для увеличения можно параллельно подключить дополнительную деталь. В этой ситуации нет необходимости заново собирать пусковую цепь.
Применяются также другие типы конденсаторов. Например, это могут быть вакуумные, жидкостные, газовые и другие. Однако в качестве пусковых конденсаторов их не используют.
Иногда тот конденсатор, который имеется в конструкции, не справляется с запуском. В таком случае его рекомендуется удалить, а вместо него поставить тот, который имеет большую ёмкость. Для маломощных двигателей допустимо, чтобы один конденсатор выполнял функции рабочего и пускового.
Использование полярных конденсаторов в условиях переменного напряжения возможно тогда, когда подключение выполнено через диод. Теперь полярность контактов изменяться не будет. Однако если диод будет неисправен, то деталь выйдет из строя.
Устройство асинхронного двигателяИсточник elektrikexpert.ru
Формулы для расчётов
Параллельное или последовательное подключение позволяет в зависимости от их комбинации добиться нужных характеристик в электрической цепи. Например, ограничить подачу тока в некоторые точки, снизить напряжение или поддерживать его на одном уровне. Для расчёта нужных параметров используют формулы для последовательного и параллельного соединения. Изначально они были получены эмпирическим путём, а затем доказаны и теоретически.
В первую очередь нужно отметить закон Ома для участка цепи. Согласно ему, сила тока в проводнике пропорциональна разности потенциалов и обратно пропорциональна сопротивлению рассматриваемого участка. Записывается закон так: I = U / R. При этом сопротивление определяется физическими и геометрическими параметрами материала.
Наряду с законом Ома, важнейшими утверждениями в электротехнике являются правила Кирхгофа. Их два:
- Алгебраическая сумма токов, сходящихся в одной точке цепи, равна нулю.
- В замкнутой электрической цепи алгебраическая сумма произведения тока на сопротивление равняется алгебраической сумме напряжений, действующих в этом контуре.
На основании закона и правил можно составить выражения, описывающие параллельное и последовательное соединение. Формулы для этих типов подключений будут следующими:

- Для последовательного: I = I1 = I2. То есть сила тока, протекающая через любой проводник, будет одинаковой для каждого из них. Связанно это с тем, что заряды не накапливаются, а через элементы проходит один и тот же заряд. Общее же напряжение будет равняться сумме падений потенциалов на каждом проводнике: U = U 1 + U2.
- Для параллельного: I = I 1 + I 2. Эта формула верна, так как в точке разветвления заряды не скапливаются, а согласно правилу Кирхгофа, поступающий заряд равен уходящему. Напряжение же будет при таком соединении одинаковым на концах любого проводника: U = U 1 + U 2.
Используя закон Ома, можно вывести формулы для нахождения сопротивления. Так, для параллельного подключения можно записать: U / R = U / R1 + U / R2. Напряжение одинаковое и на него можно сократить. В итоге формула примет вид: 1 / R = 1 / R1 + 1 / R2. Для последовательного подключения можно записать: IR = IR1 + IR2. Здесь сила тока везде одинаковая, поэтому выражение после упрощения примет вид: R = R1 + R2.
Естественно, в цепочке может находиться сколь угодно много проводников. Вид формул от этого не изменится, только добавятся дополнительные величины. Что интересно, в основе измерительных приборов лежат как раз эти законы.
https://youtube.com/watch?v=agBsAVKl19o
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
- Таким образом, протекающий общий ток в цепи можно определить как:
- I = I1 + I2
- Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
- Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
- Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
- Таким образом, общий ток будет равен:
- I = 0,545 мА + 0,255 мА = 0,8 мА
- Это также можно проверить, используя закон Ома:
- I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
- где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
- И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
Параллельное и комбинированное соединение
Выделяются другие способы соединения, а именно комбинированное и параллельное подключение конденсаторов. Для них справедливы иные физические законы.
Энергия конденсатора
Напряжение всей группы при параллельном соединёнии конденсаторов равно вольтажу самого наименьшего из них. Т.е., если имеется цепь из трёх конденсаторов на 16, 25 и 50 В, то максимум, который на них можно подать, это 16 В. В такой схеме к каждой отдельной ёмкости будет приложено полное напряжение источника питания.
Ёмкость такой батареи складывается. Вызвано это виртуальным сложением площадей обкладок всех отдельных конденсаторов. На языке физики это выглядит так:
Cобщ.пар = С1 + С2 + … + Сn.
Зачем нужно такое соединение? Оно используется для увеличения ёмкости конденсаторов, например, в высоковольтной части сварочных инверторов и многих мощных блоках питания.
Дополнительная информация. Параллельное соединение позволяет снизить общее внутреннее сопротивление сборки, следовательно, и её нагрев. Тем самым можно увеличить срок службы ёмкости.
Комбинированное (смешанное) соединение наиболее сложное. В нём встречаются как последовательные, так и параллельные элементы. Расчёт параметров таких схем даётся с опытом. Для простоты его принято изучать по треугольнику, разбивая на более простые части.
Из схемы очевидно, что конденсаторы C1 и C2 включены последовательно. Их общую ёмкость можно рассчитать по вышеописанной формуле – Cобщ.посл. Далее схема упрощается. Здесь уже имеются два параллельных конденсатора Cобщ.посл и C3. Вычисляется по вышестоящей формуле Cобщ.пар. В итоге сложный для восприятия элемент цепи превращается в один эквивалентный конденсатор. Данная методика описывает алгоритм упрощения, с помощью которого можно рассчитывать гораздо более сложные конденсаторные фигуры (квадрат, куб и т.п.).
Параллельное соединение проводников
Параллельное соединение проводников выглядит вот так.
параллельное соединение резисторов
Ну что, думаю, начнем с сопротивления.
Сопротивление при параллельном соединении проводников
Давайте пометим клеммы как А и В
В этом случае общее сопротивление RAB будет находиться по формуле
Если же мы имеем только два параллельно соединенных проводника
То в этом случае можно упростить длинную неудобную формулу и она примет вид такой вид.
Напряжение при параллельном соединении проводников
Здесь, думаю ничего гадать не надо. Так как все проводники соединяются параллельно, то и напряжение у всех будет одинаково.
Получается, что напряжение на R1 будет такое же как и на R2, как и на R3, так и на Rn
Соединение резисторов
Соединение резисторов разными способами позволяет получить необходимую величину сопротивления и мощности рассеивания одного эквивалентного резистора. Всего существует три способы соединения резисторов – последовательное, параллельное и смешанное.
Последовательное соединение резисторов
Последовательное соединение резисторов предполагает использование двух и более радиоэлектронных элемента. Конец предыдущего элемента соединяется с началом последующего и так далее. При последовательном соединении сопротивления и мощности рассеивания всех резисторов складываются. Рассмотрим следующий пример. Соединим последовательно четыре резистора, каждый имеет R = 1 кОм и мощность рассеивания P = 0,25 Вт.
Rобщ = R1 + R2 + R3 + R4 = 1кОм + 1кОм + 1кОм + 1кОм = 4 кОм.
Pобщ = P1 + P2 + P3 + P4 = 0,25 Вт + 0,25 Вт + 0,25 Вт + 0,25 Вт = 1 Вт.
Таким образом, получается один эквивалентный или общий резистор, имеющий следующие параметры: Rобщ = 4 кОм; Pобщи = 1 Вт.
В последовательной цепи электрической ток протекает одной и той же величины, поэтому электроны на протяжении всего пути неизбежно наталкиваются на все препятствия в виде сопротивлений. С каждым препятствием уменьшается число свободных зарядов, что приводит к снижению силы электрического тока.
Параллельное соединение резисторов
При параллельном соединении резисторов увеличивается количество путей для перемещения свободных зарядов, то есть электронов, из одного участка пути к другому. Поэтому при параллельном соединении резисторов их суммарное (общее, эквивалентное) сопротивление всегда ниже наименьшего сопротивления из всех резисторов.
Величина, обратная сопротивлению называется проводимостью. Проводимость измеряется в сименсах и обозначается большей латинской буквой G.
G = 1/R = 1/Ом = См
Поэтому при выполнении различных подсчетов в электрических цепях, имеющих параллельное соединение, пользуются проводимостью.
Если сопротивления всех параллельно соединенных резисторов равны, то для определения общего Rобщ достаточно R одного из них разделить на их общее количество:
Если R1 = R2 = R3 = R4 = R, то
Rобщ = R/4.
Например, каждый из четырех резисторов имеет R = 10 кОм, тогда
Rобщ = 10 кОм/4 = 2,5 кОм.
Мощности рассеивания суммируются также, как и при последовательном соединении.
Смешанное соединение резисторов
Смешанное соединение резисторов представляет собой комбинации последовательных и параллельных соединений. В принципе любую даже самую сложную электрическую цепь, состоящую из источников питания, конденсаторов, диодов, транзисторов и других радиоэлектронных элементов в конкретный момент времени можно заменить резисторами и источниками напряжения, параметры которых изменяются с каждым последующим моментом времени. Для примера изобразим схему, имеющую несколько соединений.
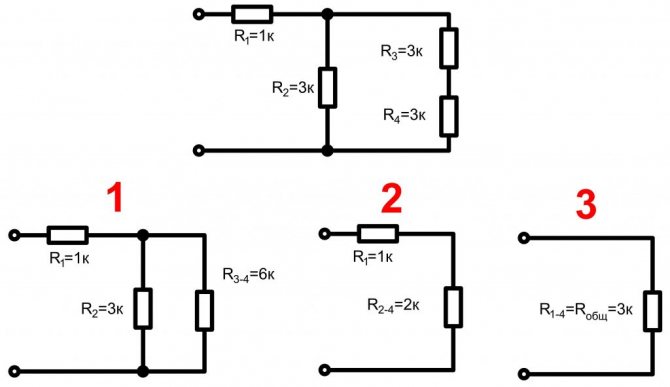
Общее (эквивалентное) сопротивление находится методом «сворачивания» схемы. Сначала определяется общее сопротивление одного отдельного соединения, затем последующего и так далее.
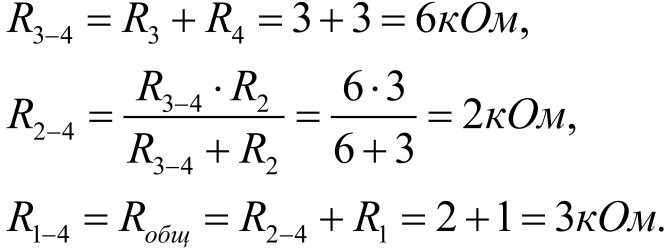
Теперь самостоятельно подсчитайте общее сопротивления схемы, приведенной ниже.
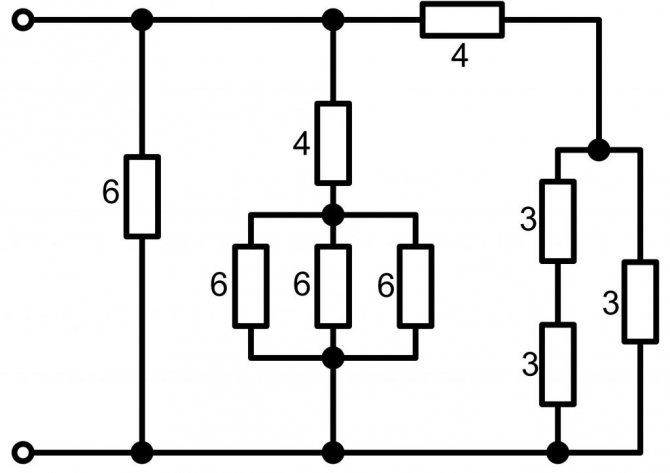
Правильный ответ: 2 ома.
Методы соединения проводов
В соответствии с п.2.1.21. ПУЭ, соединение проводов можно осуществлять только методами сварки, пайки, опрессовки и сжимов. Как видим, излюбленный метод доморощенных электриков, скрутка, не входит в перечень разрешенных методов соединения.
А из всех представленных разрешенных методов наиболее оптимальным для использования в домашних условиях является сжим. Это может быть винтовое, болтовое или пружинное соединение.
Итак:
- Для монтажа болтовых и винтовых соединений промышленность сейчас выпускает большое количество самых разнообразных клеммных соединений. Их цена достаточно не велика, а удобство монтажа находится на высоком уровне.
- Отдельно хотелось бы сказать о пружинных клеммах. Я сам не являюсь сторонников пружинок, распорок и тому подобных соединений, но как-то раз довелось стать свидетелем испытаний одного из таких клеммников.
- Это были клеммы WAGO. На испытательной установке мы плавно поднимали ток, протекающий через клемму, пока наш медный провод в 4 мм2 не перегорел. При этом величина тока составляла 100А. После этого мы достали клеммник и не обнаружили на нем никаких дефектов. Это заставило изменить мое мнение о таких пружинных клеммниках, и поэтому вам я советую присмотреться к ним повнимательнее.
- Так же стоит отметить, что отдельным преимуществом таких клеммников является возможность соединения алюминиевых и медных проводов. В обычных же условиях это можно осуществлять только через латунную вставку.
Общее сопротивление Rобщ
Для того чтобы посчитать общее сопротивление смешанного соединения:
- Цепь разбивают на участки с только пареллельным или только последовательным соединением.
- Вычисляют общее сопротивление для каждого отдельного участка.
- Вычисляют общее сопротивление для всей цепи смешанного соединения.
Так это будет выглядеть для схемы 1:
Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Можно, в соответствии схеме, сразу записывать формулу следующим образом:
- Если резисторы соединяются последоватеьно — складывать.
- Если резисторы соединяются параллельно — использовать условное обозначение «||».
- Подставлять формулу для параллельного соединения где стоит символ «||».
Так это будет выглядеть для схемы 1:
После подстановки формулы параллельного соединения вместо «||»:
Правила для различных соединений проводников
Параллельное подключение лампочек
Для обоих вариантов соединения существуют правила подсчета различных параметров электрической цепи.
Законы последовательной цепи
Законы последовательного соединения имеют такой вид:
- ток на всех участках цепочки идентичен, тогда как напряжение на ее концах равно сумме значений для каждого ее участка;
- у соединенных конденсаторов электрозаряды на обкладках примут одинаковые значения;
- когда в такую цепь соединены резисторы, ток идет в начале через первый элемент, потом через второй и, последовательно проходя все устройства, доходит до последнего (общая величина спада напряжения равна суммированным потерям его для каждого из резисторов).
Законы параллельного соединения проводников
Здесь следующая картина:
- когда электроприбор перегорает, путь электротока не блокируется, а остальные приборы не выключаются;
- ток распределяется на все распараллеленные участки и принимает на них разные значения, напряжение везде остается прежним;
- при подключении конденсаторов заряд на каждом из них равен произведению напряжения (одинакового для всех) и емкости конкретного устройства, общая емкость равна суммированным показателям всех приборов.
Смешанное соедиение проводников
Смешанное соединение – сложная конфигурация из нескольких проводников, часть из которых коммуницируют параллельно, часть – последовательно. Чтобы рассчитать значения разных показателей (ток, сопротивление и т.д.) для такого соединения, его разбивают на структурные элементы и проводят вычисления для каждого из них. При подсчете данных для укрупненных единиц их можно заменять на эквивалентные.
Примеры смешанных схем
При соединении нескольких устройств в одну цепочку важно выбрать правильный способ соединения. Если он не будет соответствовать практическим задачам, устройства не будут функционировать корректно
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. На рисунке изображёна схема участка электрической цепи АВ. В эту цепь параллельно включены два резистора сопротивлением ( R_1 ) и ( R_2 ) . Напряжения на резисторах соответственно ( U_1 ) и ( U_2 ) .
По какой из формул можно определить напряжение U на участке АВ?
2. На рисунке изображёна схема электрической цепи, содержащая два параллельно включённых резистора сопротивлением ( R_1 ) и ( R_2 ) . Какое из приведённых ниже соотношений справедливо для такого соединения резисторов?
1) ( I=I_1=I_2 ) 2) ( I=I_1+I_2 ) 3) ( U=U_1+U_2 ) 4) ( R=R_1+R_2 )
3. На рисунке изображена схема электрической цепи. В эту цепь последовательно включены два резистора сопротивлением R> и R2. Какое из приведённых ниже соотношений справедливо для такого соединения резисторов?
4. На рисунке изображена схема электрической цепи. В эту цепь последовательно включены два резистора сопротивлением ( R_1 ) и ( R_2 ) . Какое из приведённых ниже соотношений справедливо для такого соединения резисторов?
5. На рисунке изображена схема электрической цепи. В эту цепь параллельно включены два одинаковых резистора сопротивлением ( R_1 ) . По какой из формул можно определить общее сопротивление цепи ( R ) ?
6. Общее сопротивление участка цепи, изображённого на рисунке, равно 9 Ом. Сопротивления резисторов ( R_1 ) и ( R_2 ) равны. Чему равно сопротивление каждого резистора?
1) 81 Ом 2) 18 Ом 3) 9 Ом 4) 4,5 Ом
7. Чему равно сопротивление участка цепи, содержащего три последовательно соединенных резистора сопротивлением по 9 Ом каждый?

1) 1/3 Ом 2) 3 Ом 3) 9 Ом 4) 27 Ом
8. Чему равно общее сопротивление участка цепи, изображённого на рисунке, если ( R_1 ) = 1 Ом, ( R_2 ) = 10 Ом, ( R_3 ) = 10 Ом, ( R_4 ) = 5 Ом?
1) 9 Ом 2) 11 Ом 3) 16 Ом 4) 26 Ом
9. Чему равно общее сопротивление участка цепи, изображённого на рисунке, если ( R_1 ) = 1 Ом, ( R_2 ) = 3 Ом, ( R_3 ) = 10 Ом, ( R_4 ) = 10 Ом?
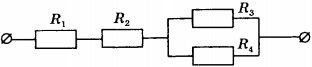
1) 9 Ом 2) 10 Ом 3) 14 Ом 4) 24 Ом
10. Если ползунок реостата (см. схему) переместить влево, то сила тока
1) в резисторе ( R_1 ) уменьшится, а в резисторе ( R_2 ) увеличится 2) увеличится в обоих резисторах 3) в резисторе ( R_1 ) увеличится, а в резисторе ( R_2 ) уменьшится 4) уменьшится в обоих резисторах
11. На рисунке изображена электрическая цепь, состоящая из источника тока, резистора и реостата. Как изменяются при передвижении ползунка реостата вправо его сопротивление, сила тока в цепи и напряжение на резисторе 1?
Для каждой физической величины определите соответствующий характер изменения. Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА A) сопротивление реостата 2 Б) сила тока в цепи B) напряжение на резисторе 1
ХАРАКТЕР ИЗМЕНЕНИЯ 1) увеличивается 2) уменьшается 3) не изменяется
12. Установите соответствие между физическими величинами и правильной электрической схемой для измерения этих величин при последовательном соединении двух резисторов ( R_1 ) и ( R_2 ) . Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ A) сила тока в резисторе ( R_1 ) и ( R_2 ) Б) напряжение на резисторе ( R_2 ) B) общее напряжение на резисторах ( R_1 ) и ( R_2 )
Часть 2
13. Три резистора соединены, как показано на рисунке. Сопротивления резисторов ( R_1 ) = 10 Ом, ( R_2 ) = 5 Ом, ( R_3 ) = 5 Ом. Каково напряжение на резисторе 1, если амперметр показывает силу тока 2 А?