7.5. Вопросы и задания для самопроверки
1. В чем заключается сущность операторного метода расчета цепи?
2. Что такое операторное сопротивление цепи?
3. Что такое операторные схемы замещения при составлении эквивалентной операторной схемы?
4.  Чем заменяются индуктивности и емкости в операторной схеме замещения?
Чем заменяются индуктивности и емкости в операторной схеме замещения?
5. Как учитываются независимые начальные условия?
6. Записать закон Ома и законы Кирхгофа в операторной форме.
7. Что такое единичная функция и d-функция?
8. Что понимается под операторной передаточной функцией? Каковы ее свойства?
9. Каким образом можно перейти от изображения к оригиналу?
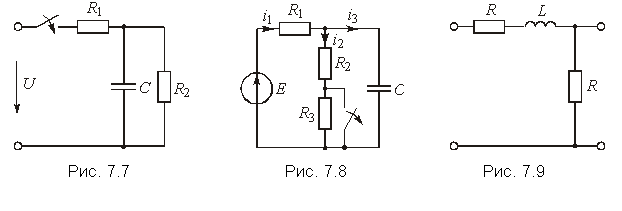
10. Для схемы, изображенной на рис. 7.7, операторным методом определить напряжение на конденсаторе uC(t). U = 20 В; R1 = = R2 = 100 Ом; С = 4 мкФ.
Ответ: uC(t) = 10 – , В.
11. Для схемы, изображенной на рис. 7.8, найти изображение тока I2(p).
Ответ: I2(p) = .
12. Зная изображение тока (рис. 7.8), определить оригинал i2(t).
Ответ: i2(t) = 2,5 – 0,825 .
13. Для схемы, изображенной на рис. 7.9, определить: 1) операторную передаточную функцию Hu(p); 2) найти АЧХ цепи. Ответ:
2.1.1. Основные понятия о переменном токе
Переменным
называется ток (ЭДС и напряжение),
периодически изменяющий свои направления
и величину. Полный период изменения
тока называется обычно периодом
переменного тока и обозначается буквой
T, а число периодов в одну секунду
называется частой f и определяется как:
f
=
.
Единица
измерения частоты
носит название герц (Гц).
В
более узком смысле под переменным током
принято понимать такой периодически
изменяющийся ток, среднее значение
которого за период равно нулю (рис.
2.1).
Рис.
2.1
В
области производства, передачи энергии
переменный ток имеет по сравнению с
постоянным два основных преимущества:
1)
возможность (при помощи трансформаторов)
просто и экономично повышать и понижать
напряжение, что имеет решающее значение
для передачи энергии на большие
расстояния;
2)
конструктивную простоту устройства
электродвигателей и генераторов, что
обуславливает их меньшую стоимость при
более высокой эксплуатационной
надёжности. Источниками электрической
энергии в цепях переменного тока являются
генераторы переменного тока.
9.7. Связь между временными и частотными характеристиками электрических цепей
Временной и частотный методы анализа переходных процессов базируются на двух взаимосвязанных характеристиках электрических цепей: импульсной или переходной, с одной стороны, и комплексной передаточной функции, с другой. Между этими характеристиками существует однозначное соответствие. Определим эту связь. Допустим, что на вход пассивной электрической цепи с комплексной передаточной функцией H(jw) приложено воздействие в виде единичной импульсной функции. Тогда с учетом того, что спектр единичного импульсного сигнала равен единице, спектр выходного сигнала согласно (9.51) будет:
Обратное преобразование (9.7) определит выходной сигнал f2(t), который численно равен импульсной характеристике цепи:
Аналогично с учетом условия физической реализуемости (8.14) можно записать прямое преобразование Фурье:
Таким образом, приходим к важному выводу: импульсная и комплексная передаточные функции пассивной электрической цепи связаны между собой парой преобразования Фурье (9.62) и (9.63). А это, в свою очередь, означает, что импульсная характеристика однозначным образом определяет комплексную передаточную функцию цепи и наоборот
Причем, для h(t) и H(jw) справедливы все свойства и теоремы. Основные теоремы спектрального анализа. В частности, из теоремы изменения масштаба независимого переменного следует, что чем более растянута во времени импульсная характеристика цепи, тем уже ее АЧХ и наоборот. Условия безыскаженной передачи сигналов через линейную цепь было показано, что для неискажающей линейной цепи АЧХ должна быть равномерна, а это соответствует согласно (9.40) импульсной характеристике цепи в виде d-функции, что полностью подтверждает изложенное.
Связь комплексной передаточной функции с переходной характеристикой также определяется однозначно, поскольку последняя связана соотношением (8.2) с импульсной характеристикой цепи. Для установления этой связи можно воспользоваться интегральным представлением единичной функции (9.58):
с учетом формулы Эйлера (3.18) перепишем (9.64):
Если ко входу электрической цепи с передаточной функцией H(jw) = |H(jw)|ejj(w) приложена единичная функция (9.65), то сигнал на выходе цепи будет численно равен переходной характеристики g(t), спектр которой определяется согласно (9.51), где . Тогда после применения обратного преобразования Фурье с учетом (9.65) получим:
или
где
Таким образом, зная Н(jw), можно найти с помощью (9.66) также и g(t)
Важно отметить предельное соотношение между g(t) и Н(jw), вытекающее непосредственно из свойств (7.17)—(7.18) и связи между преобразованием Фурье и Лапласа:
Эти соотношения означают, что реакция на выходе цепи от единичного воздействия в установившемся режиме будет отлична от нуля, если передаточная функция на нулевой частоте не равна нулю (есть путь постоянной составляющей). И напротив, в начальный момент при t = 0 (момент коммутации) реакция на выходе будет изменяться скачком, если Н(¥) — не равна нулю, т. е. цепь имеет бесконечно большую полосу пропускания. Рассмотренные соотношения хорошо иллюстрируются условиями пропускания сигнала через линейную цепь.
В заключение рассмотрим связь между вещественной Н1(w) и мнимой Н2(w) частями комплексной передаточной функции (4.7). Перепишем (9.62) в форме
Отсюда, учитывая (4.7) и (4.8), получаем
Согласно условия физической реализуемости (8.14) при t < 0 h(t) = 0, поэтому (9.69) принимает вид
Отсюда, почленно складывая и вычитая (9.69) и (9.70), получаем уравнения связи импульсной характеристики с вещественной и мнимой частями комплексной передаточной функции H(jw):
Таким образом, для нахождения импульсной характеристики цепи достаточно воспользоваться частотной зависимостью только вещественной или мнимой частей H(jw). Из (9.71) следует также важный вывод о том, что нельзя независимо выбирать вещественную и мнимую части передаточной функции или, что то же самое, нельзя произвольно выбирать АЧХ и ФЧХ цепи, так как они связаны между собой определенной зависимостью (4.9), (4.10).
7.3. Расчет переходных процессов операторным методом
Пользуясь основными свойствами преобразования Лапласа, можно получить основные законы теории цепей в операторной форме. Рассмотрим, например, последовательный RLC-контур (см. рис. 6.14), находящийся при ненулевых начальных условиях uC(0–) ¹ 0; iL(0–) ¹ 0. Для этого контура уравнение по ЗНК имеет вид:
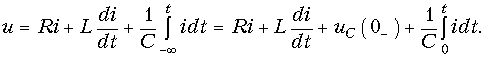
Применив к (7.33) прямое преобразование Лапласа и принимая во внимание свойства линейности, дифференцирования и интегрирования оригинала получим:
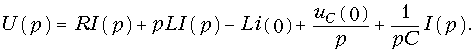
Отсюда получаем закон Ома в операторной форме для данной цепи:
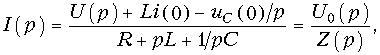
где U(p) = U(p) + Li(0) — uC(0)/p носит название операторного напряжения; Z(p) = R + pL + 1/pC — операторного сопротивления цепи. Если в Z(p) заменить р на jw, то получим комплексное сопротивление цепи. Величины Li(0) и uC(0)/p называют расчетными напряжениями. Они характеризуют энергию магнитного и электрического полей, запасенную в L и С к моменту коммутации. Величина, обратная Z(p) называется операторной проводимостью цепи:
Для нулевых начальных условий закон Ома примет вид
Аналогичным образом можно получить законы Кирхгофа в операторной форме:
первый закон (ЗТК)
второй закон (ЗНК)
Таким образом, закон Ома и законы Кирхгофа в операторной форме аналогичным этим же законам в комплексной форме (см. (3.48)—(3.50)) с той лишь разницей, что в (7.37) в каждой из п ветвей при наличии ненулевых начальных условий действуют дополнительные расчетные источники Lkik(0) и —uCk(0)/р, положительное направление которых совпадает с выбранным положительным направлением тока в этой ветви.
Используя законы Ома и Кирхгофа в операторной форме, можно найти изображения искомых токов и напряжений в цепи. Для определения оригиналов токов и напряжений можно воспользоваться либо таблицами оригиналов и изображений, либо применить теорему разложения.
Для иллюстрации основных теоретических положений найдем операторным методом закон изменения тока в последовательном RLC-контуре при включении его на источник постоянного напряжения. Уравнение для изображения тока можно найти по закону Ома для нулевых начальных условий (7.35) с учетом изображения постоянного напряжения U(p) U/p:
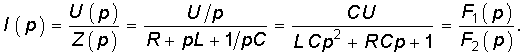
Найдем корни характеристического уравнения
При R > 2r корни будут вещественны и различны. Для нахождения оригинала тока i(t) воспользуемся теоремой разложения (7.30). Для этого найдем производные F2¢(p1) и F2¢(p2):
Подставив значения F1(p) = F1(p2) = CU и F2¢(p1) и F2¢(p2) в (7.30) получим оригинал тока
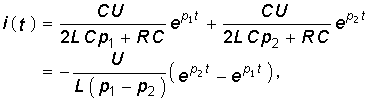
что полностью совпадает с ранее полученным уравнением (6.68).
Из рассмотренного примера хорошо видны преимущества операторного метода: простота, отсутствие громоздких операций по определению постоянных интегрирования. Следует подчеркнуть, что базируясь на законах Ома и Кирхгофа в операторной форме, можно рассчитать переходный процесс любым из ранее рассмотренных методов: контурных токов, узловых напряжений и др. При этом удобно пользоваться эквивалентными операторными схемами. При составлении эквивалентных операторных схем источники тока и напряжений i(t) и u(t) заменяются соответствующими изображениями I(p) и U(p), индуктивность L заменяется на pL, а емкость С — на 1/pC при нулевых начальных условиях. Если начальные условия ненулевые, то последовательно с pL добавляется источник напряжения Li(0), а с С — источник напряжения — uC(0)/р (рис. 7.5)
* Возможны схемы замещения заряженной емкости uC(0) и индуктивности с током iL(0) с помощью источников тока с задающими токами CuC(0) и iL(0)/p соответственно.
Например, эквивалентная операторная схема для цепи, изображенной на рис. 6.17, будет иметь вид (рис. 7.6). Составив для этой схемы уравнения по законам Кирхгофа в операторной форме, получим систему алгебраических уравнений, решение которых существенно проще системы (6.86).
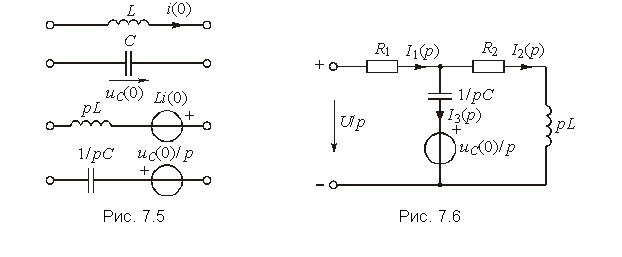
Операторный метод можно использовать и для решения уравнения состояния цепи. При этом уравнение состояния (6.94) с учетом свойств дифференцирования оригинала и линейности преобразования Лапласа примет вид:
где Х(р), W(p) — изображения векторов состояния x(t) и входных воздействий W(t).
Из (7,38) получаем непосредственно решение
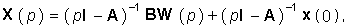
где I — единичная матрица. Применив к (7.39) теорему разложения, можно получить искомый вектор состояния
Переходные процессы при включении на постоянное напряжение разомкнутой и замкнутой на конце линии
При
замыкании рубильника (см. рис. 2) напряжение
в начале линии сразу же достигает
величины
,
и возникают
прямые волны прямоугольной формы
напряженияи
тока,
перемещающиеся вдоль линии со скоростью
V (см. рис. 3,а).Во всех точках линии, до
которых волна еще не дошла, напряжение
и ток равны нулю.Точка, ограничивающая
участок линии, до которого дошла волна,
называетсяфронтом волны.В
рассматриваемом случае во всех точках
линии, пройденных фронтом волны,
напряжение равно,
а ток -.
Отметим,
что в реальных условиях форма волны,
зависящая от внутреннего сопротивления
источника, параметров линии и т.п., всегда
в большей или меньшей степени отличается
от прямоугольной.
Кроме
того, при подключении к линии источника
с другим законом изменения напряжения
форма волны будет иной. Например, при
экспоненциальном характере изменения
напряжения источника (рис. 4,а) волна
будет иметь форму на рис. 4,б.
В
рассматриваемом примере с прямоугольной
волной напряжения при первом пробеге
волны напряжения и тока (см. рис. 3,а)
независимо от нагрузки имеют значения
соответственно
и,
что связано с тем, что волны еще не дошли
до конца линии, и, следовательно, условия
в конце линии не могут влиять на процесс.
В
момент времени
волны
напряжения и тока доходят до конца линии
длиной l, и нарушение однородности
обусловливает появление обратных
(отраженных) волн. Поскольку в конце
линия разомкнута, то
,
откуда
и.
В
результате (см. рис. 3,б) напряжение в
линии, куда дошел фронт волны, удваивается,
а ток спадает до нуля.
В
момент времени
,
обратная волна напряжения, обусловливающая
в линии напряжение,
приходит к источнику, поддерживающему
напряжение.
В результате возникает волна напряженияи
соответствующая волне тока(см.
рис. 3,в).
В
момент времени
волны
напряжения и тока подойдут к концу
линии. В связи с ХХи(см.
рис. 3,г). Когда эти волны достигнут начала
линии, напряжение и ток в ней окажутся
равными нулю. Следовательно, с этого
момента переходный процесс будет
повторяться с периодичностью.
В
случае короткозамкнутой на конце линии
в интервале времени
картина
процесса соответствует рассмотренной
выше. При,
поскольку в конце линиии,
что приведет к возрастанию тока в линии
за фронтом волны до величины.
Приот
источника к концу линии будет двигаться
волна напряженияи
соответствующая ей волна тока,
обусловливающая ток в линии, равный,
и т. д. Таким образом, при каждом пробеге
волны ток в линии возрастает на.
Отметим,
что в реальном случае, т.е. при наличии
потерь мощности, напряжение в линии в
режиме ХХ постепенно выйдет на уровень,
определяемый напряжением источника,
а ток в режиме КЗ ограничится активным
сопротивлением и проводимостью линии,
а также внутренним сопротивлением
источника.
ПОНЯТИЕ О ПЕРЕХОДНЫХ ПРОЦЕССАХ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Установившимися называются процессы, при которых напряжения и токи в цепи являются неизменными (постоянными) или синусоидальными периодическими. Переходным называют процесс в электрической цепи при переходе от одного установившегося режима к другому. Такой процесс возникает, например, при резком изменении сопротивления цепи. Если в электрической цепи имеются только источники ЭДС или тока и активные сопротивления, то переход от одного установившегося режима к другому происходит мгновенно, т. е. без переходного процесса. Возникновение переходного процесса объясняется тем, что в индуктивностях и емкостях цепи энергия не может измениться мгновенно, т. е. скачком. Для того чтобы в цепи с индуктивностью или емкостью токи или напряжения перешли от одного установившегося значения к другому, требуется время.
Длительность переходного процесса теоретически равна бесконечности. В практических расчетах с погрешностью до 3% полагают эту длительность равной Зτ, где τ — постоянная времени цепи. В расчетах с погрешностью до 1 % длительность переходного процесса считают равной 5τ.
В основу расчетов переходных процессов положены законы коммутации.
Первый закон коммутации: ток в цепи с индуктивностью не может измениться скачком.
Второй закон коммутации: напряжение на емкости не может измениться скачком.
Физический смысл первого закона коммутации заключается в том, что запас энергии в индуктивности определяется током в ней, т. е.
WL = Li2/2.
Так как энергия не может изменяться скачком, то, следовательно, и ток в индуктивности не изменяется скачком.
Запас энергии в емкости определяется напряжением на ней, т. е.
WC = Cu2/2.
Так как энергия не может измениться скачком, то, следовательно, напряжение на емкости не изменяется скачком.
Рассмотрим простейший пример переходного процесса: включение RL-цепи на постоянное напряжение U с помощью ключа S (рис. 1а).
Рис. 1. Пример переходного процесса
В этом случае до замыкания ключа ток в цепи отсутствует (I∞1=0), т. е. первый (исходный) установившийся режим заключается в равенстве тока нулю. Второй установившийся режим заключается в прохождении по цепи тока I∞2= U/R (индуктивность для постоянного тока не представляет сопротивления). В переходном процессе ток i в цепи плавно возрастает по экспоненциальному закону от нулевого значения (первый режим) до значения U/R (второй режим).
Ток в цепи называется переходным и описывается выражением
Можно представить, что ток в цепи состоит из двух составляющих (рис. 1б):
iпр+iсв
где iпр = I∞2 —принужденный; iCB = I∞2e-tTa — свободный.
Здесь е = 2,72… — основание натуральных логарифмов; Ta=L/R —постоянная времени цепи.
На рис. 1б приведены временные диаграммы переходного тока и его принужденной и свободной составляющих.
В электрических сетях при КЗ Та = 0,3 + 0,01 с, в распределительных сетях Та=0,05 с.
Переходные процессы в сложных электрических цепях при включении на постоянное или синусоидальное питающее напряжение рассчитывают с помощью операционного исчисления, а при включении на напряжение произвольной формы — при помощи интеграла Дюамеля.
Процессы в цепях при прохождении по ним коротких импульсов (длительностью в единицы — сотни микросекунд) называются волновыми. Волновые процессы возникают, например, при ударах молнии в линию, а также при коммутациях (включениях и отключениях) электрических цепей с индуктивными или емкостными элементами. Опасность волновых процессов заключается в возможности появления во время их существования импульсных перенапряжений, не допустимых для изоляции электротехнического оборудования. С целью защиты оборудования от таких перенапряжений устанавливают специальные устройства — разрядники и ограничители перенапряжений (ОПН).
Как починить гнездо для зарядки телефона
Чтобы отремонтировать сломанное гнездо аккумулятора смартфона, необходимы следующие инструменты:
- острый тонкий нож или пластиковая карта;
- несколько маленьких крестовых отвёрток;
- провод на минус;
- новый USB-порт;
- паяльник;
- пинцет.
Пошаговая инструкция ремонта гнезда для зарядки:
- Разбираем корпус портативного гаджета, используя при этом отвёртки и острый тонкий нож или пластиковую карту.
- Обязательно следует припаять провод на минус с корпусом телефона, а второй конец присоединить к паяльнику. Это действие поможет избежать удара током.
- Маленькой крестовой отвёрткой нужно извлечь винты, которые придерживают материнскую плату устройства.
- Достать открученное комплектующие.
- Найти USB-разъём на материнской плате.
- Аккуратно извлечь сломанное гнездо зарядки при помощи паяльника.
- Впаять новый USB-порт.

После выполнения всех этапов собираем мобильное устройство в единое целое. Если инструкция была выполнена правильно, то зарядка телефона будет проходить без проблем.
Два закона коммутации
-
В индуктивном элементе ток (и магнитный поток) непосредственно после коммутации в момент, который и назван моментом коммутации t=0+ , или, короче, t=0, сохраняет значение, которое он имел непосредственно перед коммутацией, т. е. при t=0-, и дальше начинает изменяться именно с этого значения:
Так, при включении ветви с катушкой, в которой не было тока, ток в этой ветви в момент коммутации равен нулю. Если для такой ветви допустить, что в момент коммутации ток изменится скачком, то напряжение на индуктивном элементе будет бесконечно большим, и в цепи не будет выполняться второй закон Кирхгофа.
-
На емкостном элементе напряжение (и заряд) сохраняет в момент коммутации то значение, которое оно имело непосредственно перед коммутацией, и в дальнейшем изменяется, начиная именно с этого значения:
Так, при включении ветви с конденсатором, который не был заряжен, напряжение на конденсаторе в момент коммутации равно нулю. Если допустить, что в момент коммутации напряжение на емкостном элементе изменяется скачком, то ток будет бесконечно большим, и в цепи не будет выполняться опять-таки второй закон Кирхгофа.
С энергетической точки зрения невозможность мгновенного изменения тока и напряжения объясняется невозможностью скачкообразного изменения запасенной в индуктивном и емкостном элементах энергии (энергии магнитного поля и энергии электрического поля ). Действительно, скачкообразное изменение энергии требует бесконечно больших мощностей, что лишено физического смысла, так как реальные источники питания не обладают бесконечно большой мощностью и не могут ее обеспечить.
В этом разделе рассматриваются переходные процессы в линейных электрических цепях с сосредоточенными параметрами. Поэтому исключается из рассмотрения нелинейный элемент — электрическая дуга, которая может возникнуть при коммутациях. Чтобы исключить влияние дуги, будем считать, что длительность коммутации по сравнению с продолжительностью переходного процесса очень мала, т. е. теоретически мгновенная.
Записанные выше законы коммутации для тока и напряжения в ветвях, содержащих реактивные элементы, при некоторых коммутациях не выполняются. Такие коммутации называют «некорректными» (приводят к требованию скачкообразных изменений токов и напряжений ). Расчет переходных процессов в таких цепях рассматривается в разделе.
Дополнительно по теме
- Переходные процессы в электрических цепях
- Переходный, установившийся и свободный процессы
- Короткое замыкание rL-цепи
- Включение rL-цепи на постоянное напряжение
- Включение rL-цепи на синусоидальное напряжение
- Короткое замыкание rС-цепи
- Включение rC-цепи на постоянное напряжение
- Включение rC-цепи на синусоидальное напряжение
- Переходные процессы в rС-цепи
- Апериодическая разрядка конденсатора
- Предельный случай апериодической разрядки конденсатора
- Периодическая (колебательная) разрядка конденсатора
- Включение rLC-цепи на постоянное напряжение
- Общий случай расчета переходных процессов классическим методом
- Пример классического метода
- Переходные процессы в цепях с взаимной индуктивностью
- Включение пассивного двухполюсника к источнику непрерывно меняющегося напряжения
- Включение пассивного двухполюсника к источнику напряжения произвольной формы
- Переходная и импульсная переходная характеристики
- Запись интеграла Дюамеля при помощи импульсной переходной характеристики
- Метод переменных состояния
- Численные методы решения уравнений состояния
- Дискретные модели электрической цепи
- Переходные процессы при некорректных коммутациях
- Определение переходного процесса при воздействии периодических импульсов напряжения
Общие понятия о параллельной работе электрических машин
Под параллельной работой нескольких трансформаторов понимается такая работа, когда их вторичные обмотки подключены к общей нагрузки, а первичные обмотки получают питание от одной сети. Параллельная работа находит широкое применение в электрических системах. При параллельной трансформатора следует стремится к тому, что бы каждый из них был нагружен токами, пропорциональными их номинальным мощностям. Для этого необходимо, что бы трансформаторы, включаемые на параллельную работу, имели равные первичные и вторичные номинальные напряжения, а как следствия и одинаковые коэффициенты трансформации, одинаковые группы соединения обмоток, одинаковые напряжения КЗ , ΔPкз→min.
Параллельная работа генераторов постоянного тока
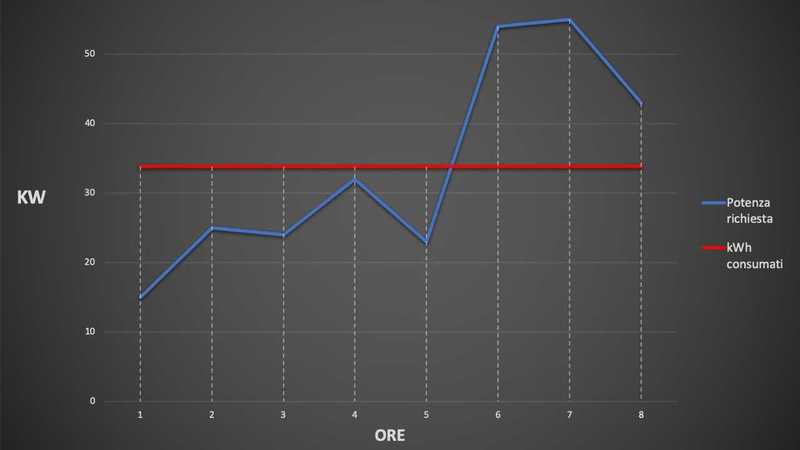
Под параллельной работой понимается работа нескольких генераторов на общую нагрузку. Необходимость в параллельной работе возникает при переменном характере нагрузки, когда она меняется в течении суток или времени года, и для повышения надежности питания.
1.1. Общие сведения
Процесс
перехода режима работы электрической
цепи от одного к другому называетсяпереходным.
В течение переходного процесса мгновенные
значения напряжений и токов не являются
периодическими функциями времени.
Переходный
процесс может быть вызван различными
причинами: например, подключением цепи
к источникам, изменением параметров
элементов или схемы цепи. В общем случае
в электротехнике принято, что возникновение
переходного процесса связано с явлениемкоммутации.
Принимается допущение, что коммутация
начинается в момент времениt
(обычноt
0) и совершается мгновенно:t
0. При этом различают два момента
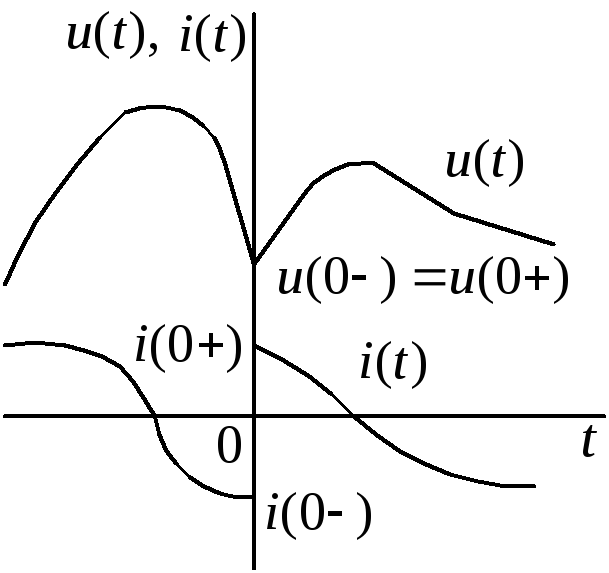
времени: момент времени
|
непосредственно
На рис. 1.1 показан |
Рис. 1.1 |
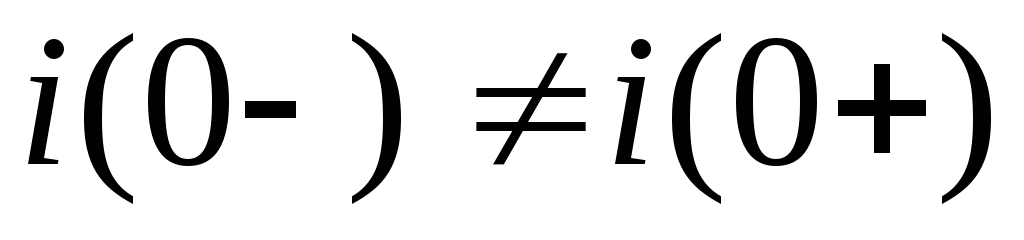 .
.
Энергия
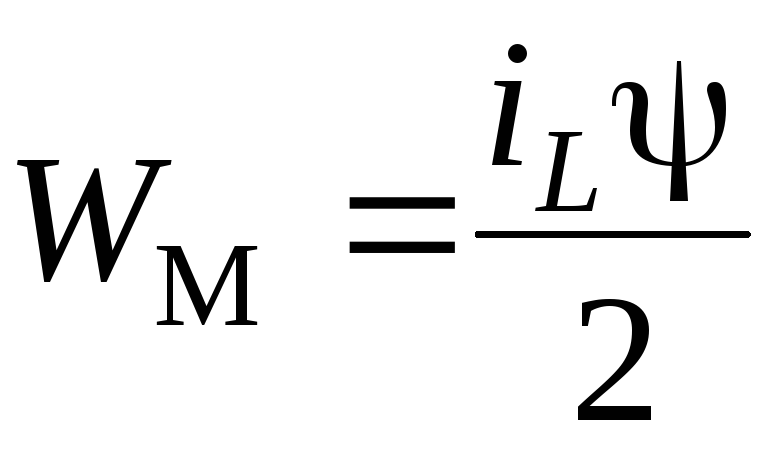 L
L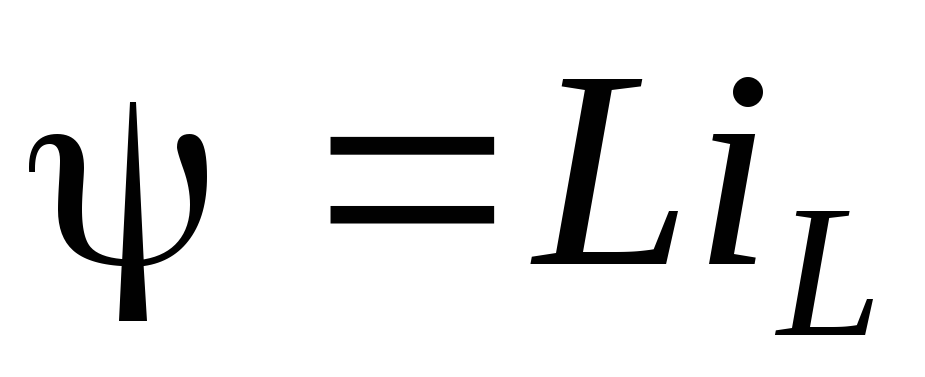
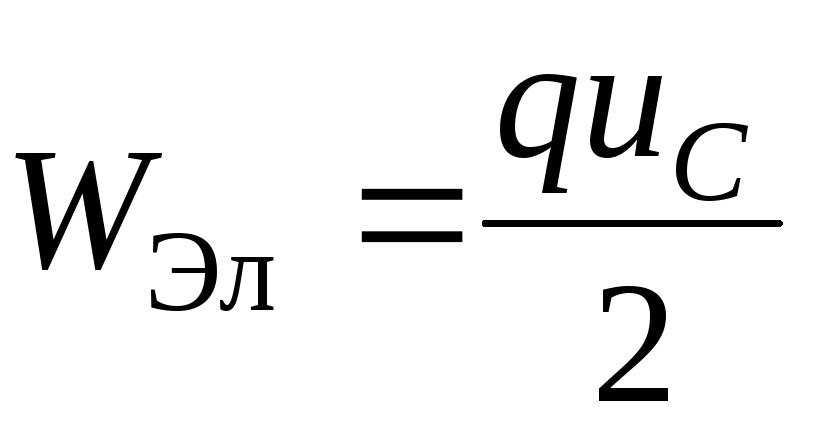 СqCuC
СqCuC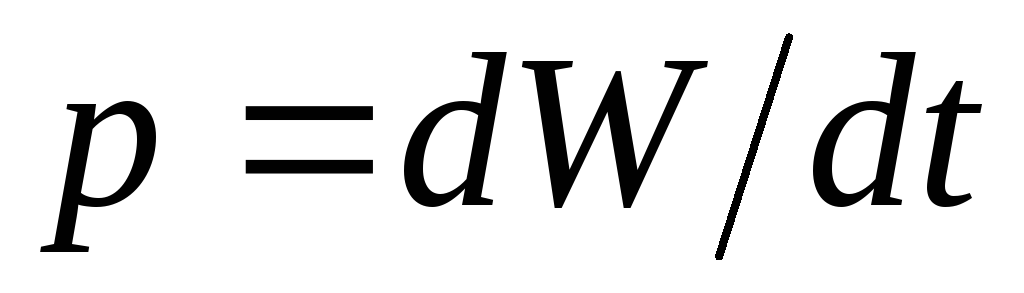
При мгновенной
коммутации WМ(–0)
WМ(+0);WЭл(–0)
WЭл(+0),
т. е. энергия, запасенная в магнитном
или электрическом поле, в момент
коммутации скачком не меняется. Это
положение постулируетсяпринципами
непрерывности потокосцепленияиндуктивности и электрического зарядаq
емкости. Действительно, при скачкообразном
изменении потокосцеплениянапряжение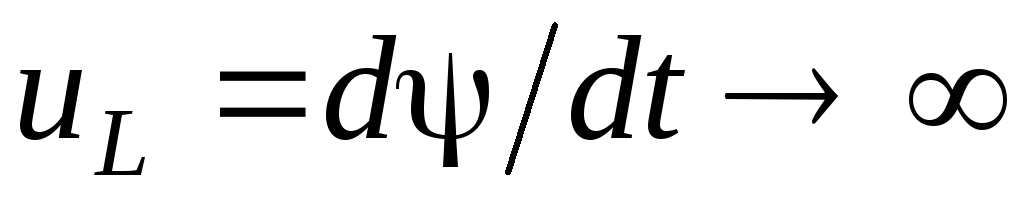 ,а при скачкообразном
,а при скачкообразном
изменении электрического зарядаqток емкости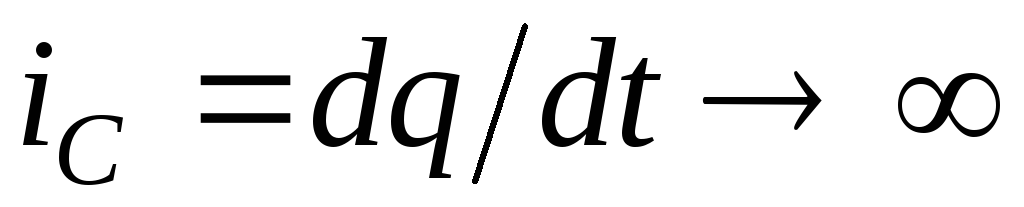 .
.
То и другое лишено физического смысла.
Поскольку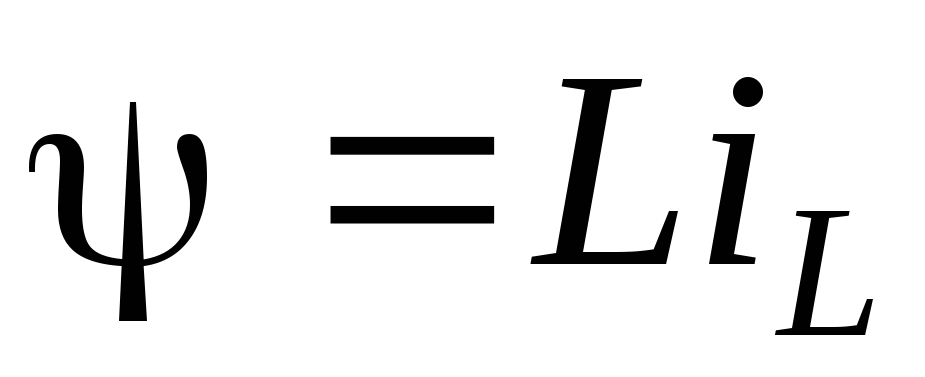 ,
,
то при неизменномLток в индуктивности не может меняться
скачком. Отсюда следует закон коммутации
для ветви с индуктивностью:в
момент коммутации ток в ветви с
индуктивностью скачком не меняется и
в переходном процессе начинает изменяться
с того значения, которое было в момент
времени, непосредственно предшествующий
коммутации, т. е.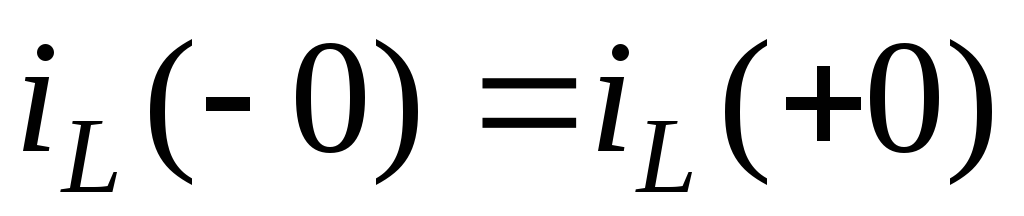
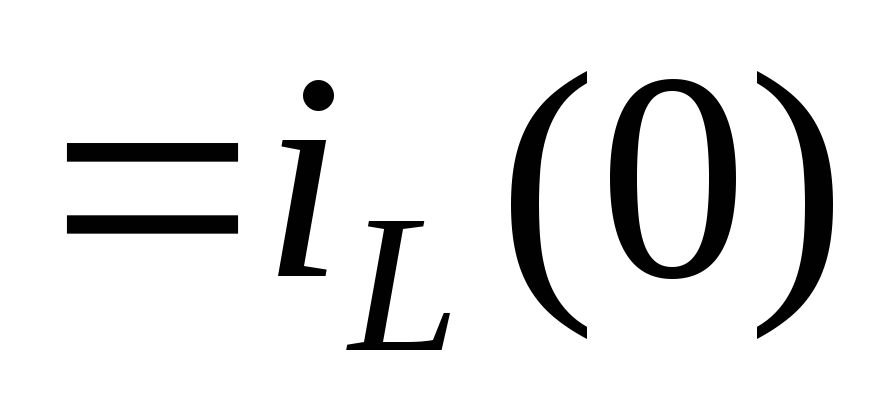 .
.
Из равенства q
CuCследует, что при неизменной величинеСнапряжениеuСне может меняться скачком. Отсюда следует
закон коммутации для емкости:в
момент коммутации напряжение на емкости
скачком не меняется и в переходном
процессе начинает изменяться с того
значения, которое было в момент времени,
непосредственно предшествующий
коммутации, т. е.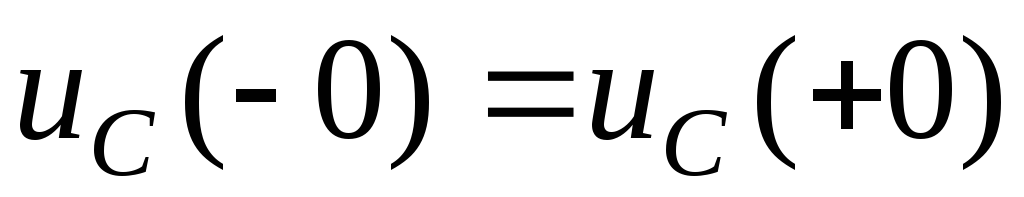
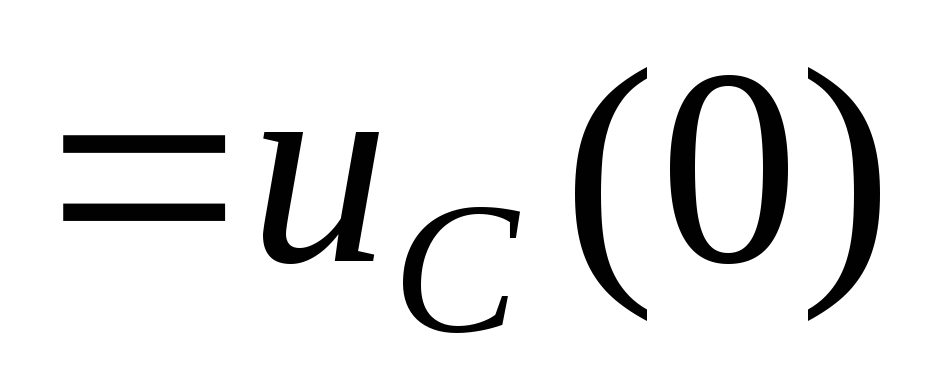 .
.
Значения
тока в индуктивности
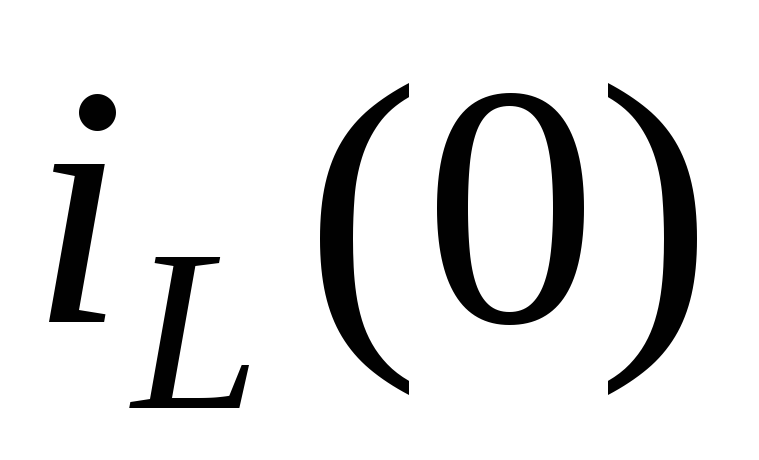
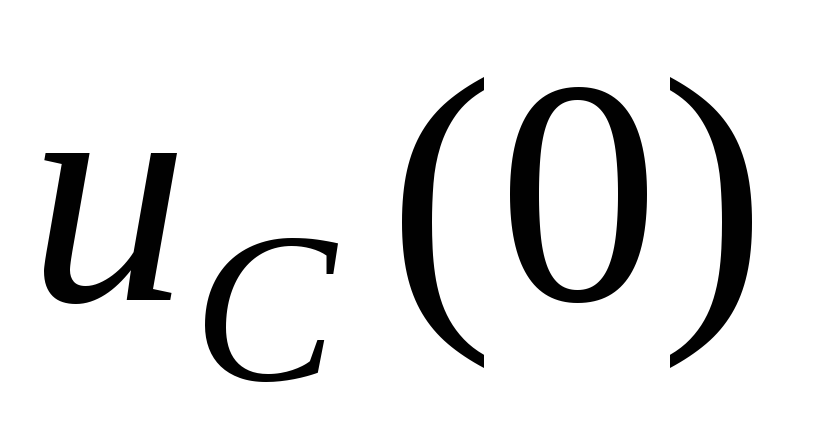 независимыми
независимыми
физическими начальными условиями
Математическая
модель цепи в переходном процессе
строится на основе
уравнений по
законам Кирхгофа и уравнений идеальных
элементов R,L,C.
Если положительные
направления напряжения и тока на элементе
одинаковы, то уравнения идеальных
элементов имеют вид:
для активного
сопротивления (резистора);
-
или
для индуктивности; -
или
для емкости.
Для
идеальных элементов R
иC
ток в момент коммутации может меняться
скачком:
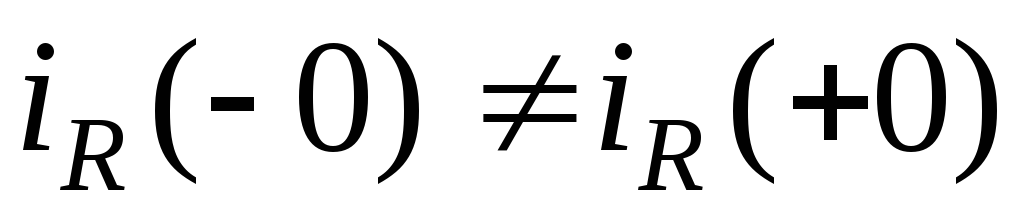 ;
;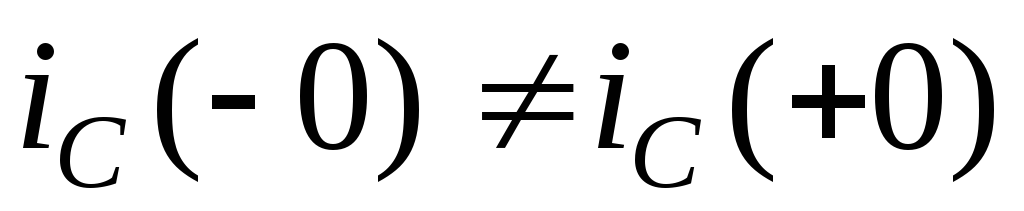 .
.
Для
идеальных элементовR
иL
в момент коммутации могут меняться
скачком напряжения:
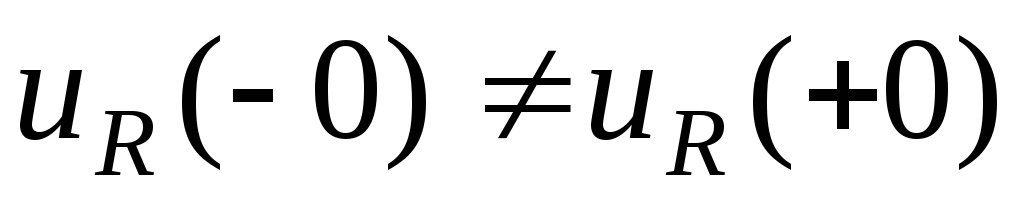 ;
;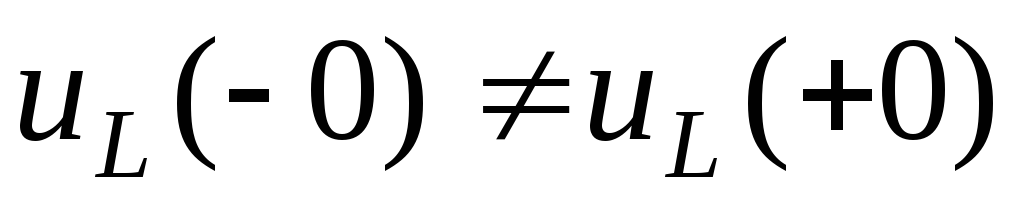 .
.
Значения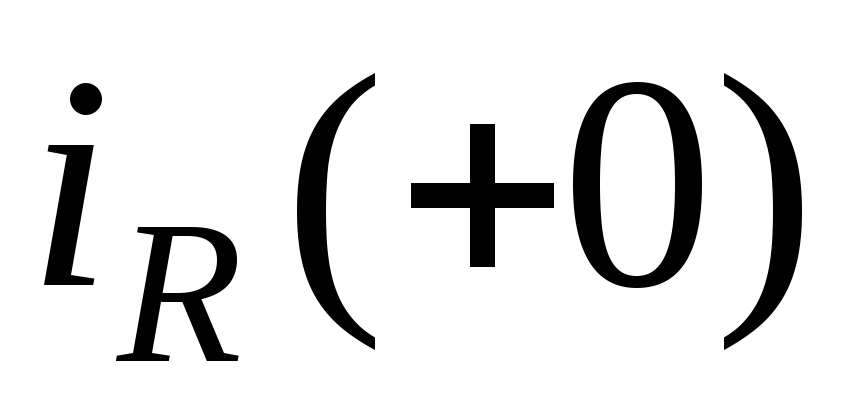 ;
;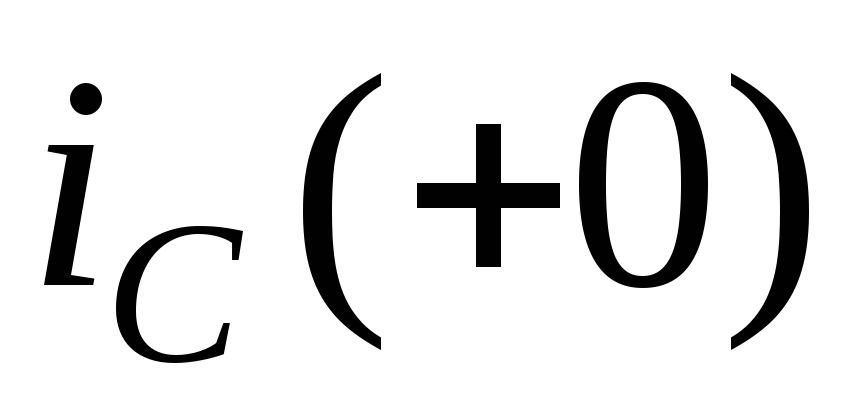 ;
;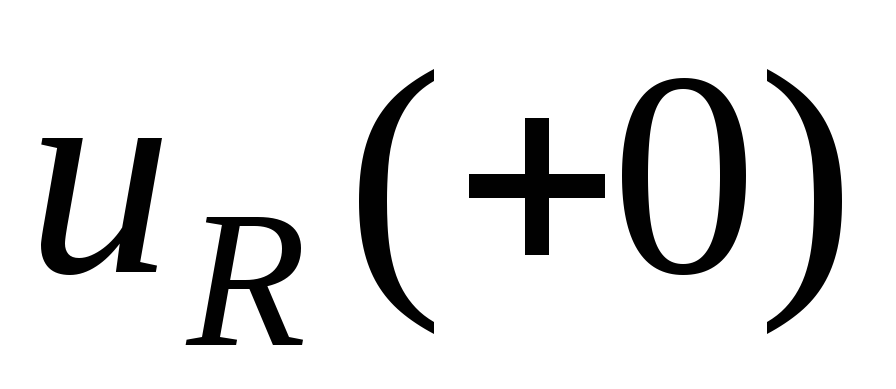 ;
;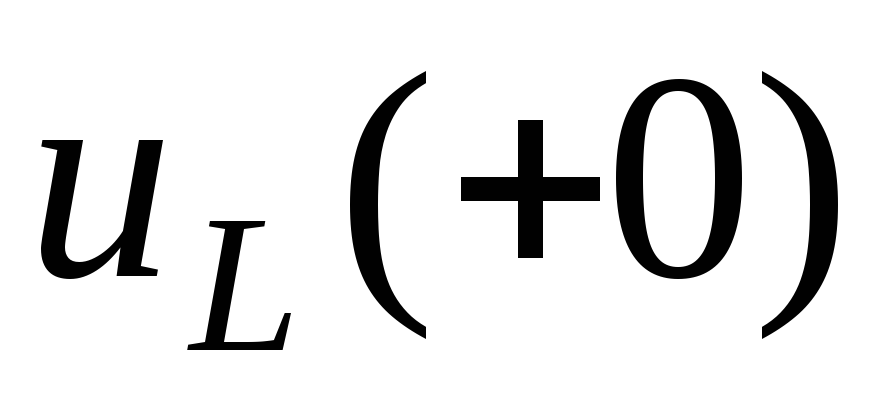 называютсязависимыми
называютсязависимыми
физическими начальными условиями.

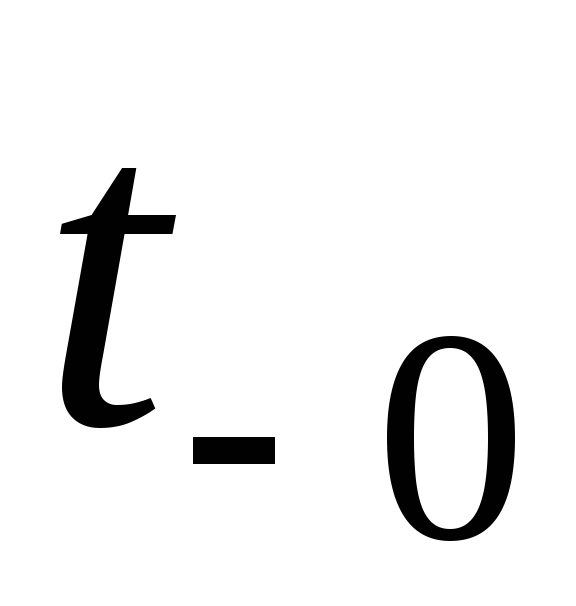 ,
,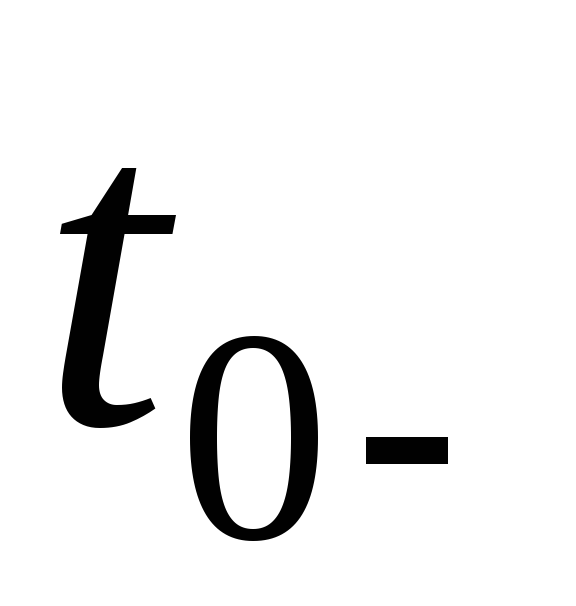 ,
, ,
,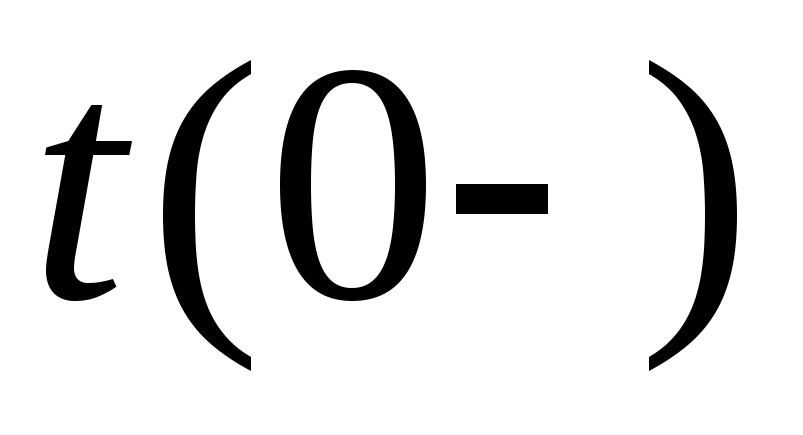 ;
;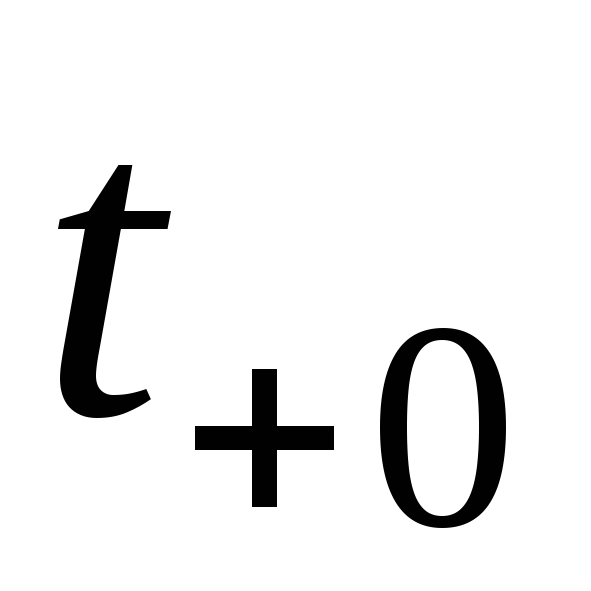 ,
, ,
,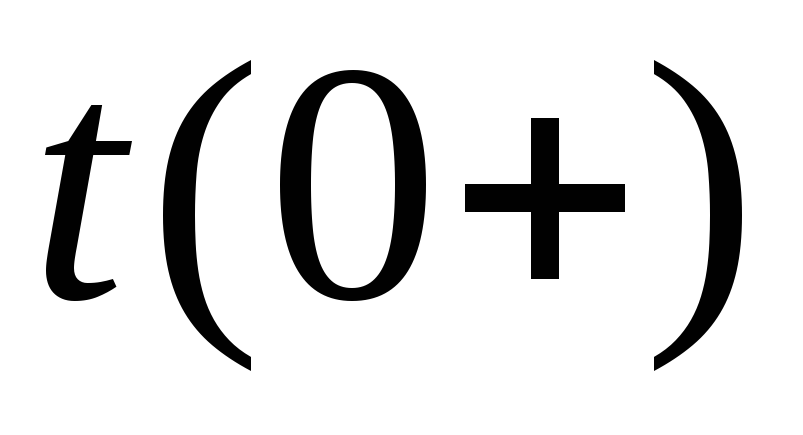 ,
,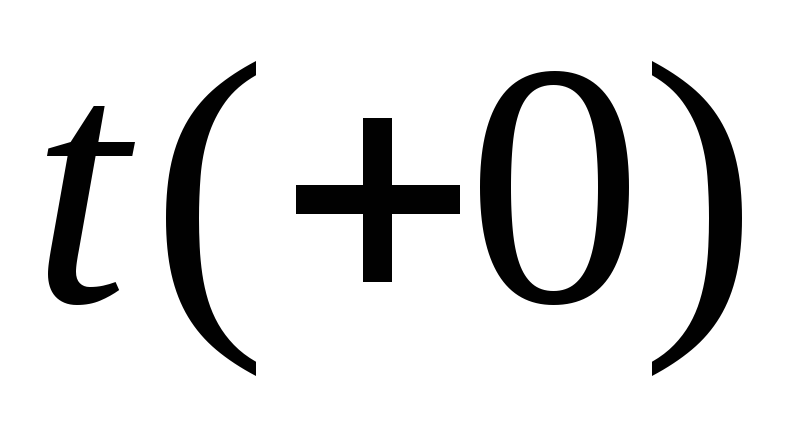 .
.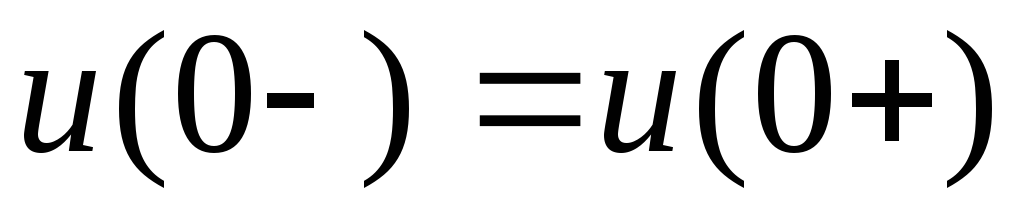 ,
,