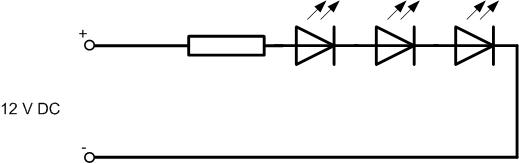
Что такое падение напряжения на резисторе
Электрический ток, проходя по цепи, испытывает сопротивление, которое может изменяться под воздействием разнообразных условий внешней среды (экстремально низкие температуры или нагрев) и может зависеть от характеристик конкретного проводника. Например, чем тоньше проводник или длиннее – тем оно выше.
На значение его величины влияют следующие факторы:
- сила тока;
- длина проводящих частей;
- напряжение;
- материал проводниковых элементов;
- нагрев (температура);
- площадь поперечного сечения.
Резисторы можно разделить на постоянные, переменные и подстроечные. Главное их отличие друг от друга – возможность изменения показателя сопротивления. Чаще всего встречаются постоянные резисторы – данный показатель в них нельзя изменить, поэтому они и получили такое название. Переменные отличаются тем, что величину сопротивления в них можно настраивать. В подстроечном резисторе её также можно изменять, но отличие данной разновидности в том, что он не рассчитан на частое изменение параметра. Подстроечные резисторы выполняются в более компактном корпусе по сравнению с переменными.
Чтобы вычислить падение напряжения на резисторе, нужно помнить, что снижение нагрузки, приложенной ко всей цепи (то есть, напряжения, подключённого к контуру) может быть получено как для всего контура, так и для любого элемента цепи. Напряжение понижается за счёт сопротивления, которым обладают проводники.
Падение напряжения на резисторе зависит от силы проходящего тока и характеристик проводников. Температура и показатели тока также имеют значение. Например, напряжение, измеренное вольтметром на лампочке, подключённой к сети 220 В, будет немного ниже за счёт сопротивления, которым обладает лампочка.
Источники питания имеют разную величину напряжения. Это значение может превышать то, которое бывает необходимо на выходе. Чтобы нагрузка, которую требуется запитать, не сгорела, часто возникает необходимость в понижении вольтажа, в том числе с помощью резисторов.
Сравнительная таблица напряжений
| Источник питания | Напряжение |
| NiCd аккумулятор | 1,2 В |
| Литий-железо-фосфатный аккумулятор | 3,3 В |
| Батарея типа «Крона» | 9 В |
| Автомобильный аккумулятор | 12 В |
| Аккумулятор для грузовых автомобилей | 24 В |
В этом случае резистор должен уменьшить протекающий по цепи ток. При этом ток не превращается в тепло, происходит именно его ограничение. То есть при включении резистора в цепь ток упадёт – в этом и состоит работа резистора, при совершении которой элемент нагревается.
В общем случае падения напряжения можно рассчитать, используя простую формулу, связывающее показатели между собой.
Но в ряде случаев, например, при параллельном подключении сопротивлений, посчитать необходимую величину уже сложнее. В этом случае по специальной формуле потребуется привести сопротивление параллельных веток к одному числу:
R = R1*R2 / (R1+R2)
При необходимости также учитываются другие сопротивления, суммирующиеся с этим значением (например, сопротивление провода и источника питания).
Параллельное соединение
В электрических схемах на участках цепи используется как параллельное, так и последовательное соединение. Первое представляет собой цепь, в которой каждый её элемент подключён к другому обоими контактами, но при этом между собственными его выводами нет прямой электрической связи. Т. е. существует две точки (электрические узлы), к которым присоединено несколько резисторов.
При таком включении ток, проходя через узел, начинает разделяться, и через каждый элемент потечёт разное его значение. Величина тока на каждом элементе будет прямо пропорциональна сопротивлению резистора, поэтому общая проводимость на этом участке увеличится, а её импеданс уменьшится.
Преобразовав эту формулу, получится выражение вида: R общ = 1/G = (R1*R2*…* Rn) / (R1*R2 + R2*Rn +…+ R1*Rn. Проанализировав его, можно сделать вывод, что при параллельном соединении импеданс всегда будет меньше самого маленького значения отдельного резистора.
https://youtube.com/watch?v=zNi6yEEXFgQ
При таком соединении напряжение между узлами одновременно является общей разностью потенциалов для всего участка и на каждом отдельно взятом резисторе. Поэтому если рассчитать падение напряжения на одном приборе, то оно будет таким же на любом параллельно подключённом элементе: U общ = U 1 = U 2 =…= U n.
Как работает делитель напряжения
Делитель напряжения это устройство, осуществляющее регулировку выходного напряжения по отношению значения входного напряжения, в соответствии с коэффициентом передачи. То есть, из большего значения получается меньшее, а само напряжение бывает постоянным или переменным. Самая простая схема делителя напряжения состоит как минимум из двух сопротивлений. Если их сопротивления равны между собой, то и падения напряжения будут одинаковыми. Поэтому, по закону Ома напряжение на выходе прибора будет ровно в два раза ниже, чем на входе. В других случаях для расчетов падения напряжений используются формулы.
Основной функцией делителя напряжения в электрических цепях является снижение напряжения и получение нескольких его значений с фиксированными показателями на различных участках. Его основой служат резисторы или реактивные сопротивления в количестве два и более элементов.
Простейший делитель представляется в виде двух участков цепи, называемых плечами. Верхним плечом считается участок между нулевой точкой и положительным напряжением, а нижним – участок между нулевой точкой и минусом. После того как определены исходные данные, можно сделать самый простой расчет делителя напряжения.
В качестве примера рассматриваются два резистора, соединенные последовательно. К ним подается напряжение U, которое может быть переменными или постоянным. После этого в действие вступает закон Ома, когда при последовательном соединении резисторов, общее сопротивление составит сумму их номиналов. В виде формы это будет выглядеть следующим образом: I = U/Rобщ, в которой Rобщ = R1+R2. Следовательно, I = U/(R1+R2).
Сила тока при последовательно соединенных резисторов, будет одинаковой на всех участках цепи. Если у каждого резистора имеется собственное значение сопротивления, то по закону Ома у них образуются совершенно разные напряжения. Сопротивлению R1 соответствует напряжение U1, а сопротивлению R2 – напряжение U2. В результате получается следующая ситуация, выраженная формулой I = U2/R2 = U1/R1 = U/(R1+R2).
Для того, чтобы найти значения напряжений U1 и U2, необходимо выполнить такие действия: U1 = U x R1/(R1+R2) и U2 = U x R2/(R1+R2). Если правые части каждого уравнения сложить друг с другом, то в результате получится значение входящего напряжения U, состоящее из суммы напряжений U1 и U2, то есть U = U1 + U2. Это значит, что сумма падений напряжений на всех последовательно соединенных резисторах, будет равна напряжению источника питания, то есть входящему напряжению. Таким образом, данное выражение есть ни что иное, как формула делителя напряжения. Практически получается, что входящее напряжение U оказалось разделенным на два напряжения с собственными значениями – U1 и U2.
Во многих случаях необходимо, чтобы процесс разделения напряжения осуществлялся плавно. С этой целью был изобретен прибор – переменный резистор. Работа устройства происходит по установленной схеме. Два крайних контакта обладают постоянным сопротивлением, а сопротивление среднего контакта относительно крайних контактов будет изменяться в зависимости от направления вращения регулятора. С помощью переменных резисторов добавляется громкость в звуковых колонках, у радиоприемников и телевизоров старых марок.
Резисторы, ток и напряжение
В этой статье мы рассмотрим резистор и его взаимодействие с напряжением и током, проходящим через него. Вы узнаете, как рассчитать резистор с помощью специальных формул. В статье также показано, как специальные резисторы могут быть использованы в качестве датчика света и температуры.
Представление об электричестве
Новичок должен быть в состоянии представить себе электрический ток. Даже если вы поняли, что электричество состоит из электронов, движущихся по проводнику, это все еще очень трудно четко представить себе. Вот почему я предлагаю эту простую аналогию с водной системой, которую любой желающий может легко представить себе и понять, не вникая в законы.
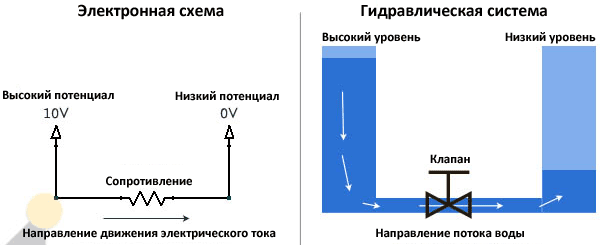
Обратите внимание, как электрический ток похож на поток воды из полного резервуара (высокого напряжения) в пустой(низкое напряжение). В этой простой аналогии воды с электрическим током, клапан аналогичен токоограничительному резистору
Из этой аналогии можно вывести некоторые правила, которые вы должны запомнить навсегда: — Сколько тока втекает в узел, столько из него и вытекает — Для того чтобы протекал ток, на концах проводника должны быть разные потенциалы. — Количество воды в двух сосудах можно сравнить с зарядом батареи. Когда уровень воды в разных сосудах станет одинаковым, она перестанет течь, и при разряде аккумулятора, разницы между электродами не будет и ток перестанет течь. — Электрический ток будет увеличиваться при уменьшении сопротивления, как и скорость потока воды будет увеличиваться с уменьшением сопротивления клапана.
Я мог бы написать гораздо больше умозаключений на основе этой простой аналогии, но они описаны в законе Ома ниже.
Резистор

Резисторы могут быть использованы для контроля и ограничения тока, следовательно, основным параметром резистора является его сопротивление, которое измеряется в Омах. Не следует забывать о мощности резистора, которая измеряется в ваттах (Вт), и показывает, какое количество энергии резистор может рассеять без перегрева и выгорания
Важно также отметить, что резисторы используются не только для ограничения тока, они также могут быть использованы в качестве делителя напряжения для получения низкого напряжения из большего. Некоторые датчики основаны на том, что сопротивление варьируется в зависимости от освещённости, температуры или механического воздействия, об этом подробно написано в конце статьи
Закон Ома
Понятно, что эти 3 формулы выведены из основной формулы закона Ома, но их надо выучить для понимания более сложных формул и схем. Вы должны быть в состоянии понять и представить себе смысл любой из этих формул. Например, во второй формуле показано, что увеличение напряжения без изменения сопротивления приведет к росту тока. Тем не менее, увеличение тока не увеличит напряжение (хотя это математически верно), потому что напряжение — это разность потенциалов, которая будет создавать электрический ток, а не наоборот (см. аналогию с 2 емкостями для воды). Формула 3 может использоваться для вычисления сопротивления токоограничивающего резистора при известном напряжении и токе
Это лишь примеры, показывающие важность этого правила. Вы сами узнаете, как использовать их после прочтения статьи
Последовательное и параллельное соединение резисторов
Понимание последствий параллельного или последовательного подключения резисторов очень важно и поможет вам понять и упростить схемы с помощью этих простых формул для последовательного и параллельного сопротивления:
В этом примере схемы, R1 и R2 соединены параллельно, и могут быть заменены одним резистором R3 в соответствии с формулой:
В случае с 2-мя параллельно соединёнными резисторами, формулу можно записать так:
Кроме того, что эту формулу можно использовать для упрощения схем, она может быть использована для создания номиналов резисторов, которых у вас нет. Отметим также, что значение R3 будет всегда меньше, чем у 2 других эквивалентных резисторов, так как добавление параллельных резисторов обеспечивает дополнительные пути электрическому току, снижая общее сопротивление цепи.
Последовательно соединённые резисторы могут быть заменены одним резистором, значение которого будет равно сумме этих двух, в связи с тем, что это соединение обеспечивает дополнительное сопротивление тока. Таким образом, эквивалентное сопротивление R3 очень просто вычисляется: R3=R1+R2
Ток
Ампер — это сила такого электрического тока, который проходя по двум прямолинейным параллельным бесконечным проводникам, расположенным на расстоянии 1 (метр) друг от друга, вызывает на каждом участке длиной 1 (метр) силу взаимодействия 2·10−7 (Ньютон). Ток по известным напряжению и сопротивлению.
Калькулятор радиолюбителя — расчет силы тока. Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
Ток по известным мощности и напряжению.
Сопротивление
Сопротивление по известным напряжению и току.
Калькулятор радиолюбителя — расчет сопротивления. Электрическое сопротивление определяет силу тока, текущего по цепи при заданном напряжении.
Напряжение
Напряжение по известным сопротивлению и току.
Калькулятор радиолюбителя — расчет напряжения. Падение напряжения на участке проводника равно произведению силы тока в проводнике на сопротивление этого участка.
Мощность
Мощность электрического тока — это отношение произведенной им работы ко времени в течение которого совершена работа.
Мощность по напряжению и току.
Мощность по напряжению и сопротивлению.
Для удобства радиолюбителей создан онлайн калькулятор радиолюбителя для расчета потребляемого тока, напряжения, удельного сопротивления потребителя и так далее. Интернет уже давно не редкость в наших домах, офисах и мастерских. Поэтому нет никакой необходимости держать в голове кучу формул и мучить калькулятор. Калькуляторы для онлайн расчетов радиолюбителя позволят не отвлекаться от творческого процесса или ремонта, что в принципе тоже является творчеством
Существует общая формула, даже не формула а свод формул, приведенных в одно целое:
Свод формул для радиолюбителя
Где:
- V — напряжение
- I — сила тока
- Р — мощность
- R — сопротивление
На этих четырех величинах держится вся электроника. Помните что правильные расчеты — пятидесяти процентный шанс на успешное завершение проекта.
Калькулятор радиолюбителя для расчета мощности , тока, сопротивления и напряжения могут применяться для вычисления требуемой мощности блока питания, необходимого напряжения для нормальной работы устройства, площади сечения провода. Кстати вот отличная таблица выбора провода по сечению и мощности.
Постоянная ссылка на это сообщение: https://rightnotes.ru/kalkulator_radiolubitelya
Применение делителя напряжения на резисторах
В радиоэлектронике есть много способов применения делителя напряжения. Вот только некоторые примеры где вы можете обнаружить их.
Потенциометры
Потенциометр представляет собой переменный резистор, который может быть использован для создания регулируемого делителя напряжения.
Изнутри потенциометр представляет собой резистор и скользящий контакт, который делит резистор на две части и передвигается между этими двумя частями. С внешней стороны, как правило, у потенциометра имеется три вывода: два контакта подсоединены к выводам резистора, в то время как третий (центральный) подключен к скользящему контакту.
Если контакты резистора подключения к источнику напряжения (один к минусу, другой к плюсу), то центральный вывод потенциометра будет имитировать делитель напряжения.
Переведите движок потенциометра в верхнее положение и напряжение на выходе будет равно входному напряжению. Теперь переведите движок в крайнее нижнее положение и на выходе будет нулевое напряжение. Если же установить ручку потенциометра в среднее положение, то мы получим половину входного напряжения.
Резистивные датчики
Большинство датчиков применяемых в различных устройствах представляют собой резистивные устройства. Фоторезистор представляет собой переменный резистор, который изменяет свое сопротивление, пропорциональное количеству света, падающего на него. Так же есть и другие датчики, такие как датчики давления, ускорения и термисторы и др.
Так же резистивный делитель напряжения помогает измерить напряжение при помощи микроконтроллера (при наличии АЦП).
Пример работы делителя напряжения на фоторезисторе.
Допустим, сопротивление фоторезистора изменяется от 1 кОм (при освещении) и до 10 кОм (при полной темноте). Если мы дополним схему постоянным сопротивлением примерно 5,6 кОм, то мы можем получить широкий диапазон изменения выходного напряжения при изменении освещенности фоторезистора.
Как мы видим, размах выходного напряжения при уровне освещения от яркого до темного получается в районе 2,45 вольт, что является отличным диапазоном для работы большинства АЦП.
Стенд для пайки со светодиодной подсветкой
Материал: АБС + металл + акриловые линзы. Светодиодная подсветка…
Подробнее
Базовые формулы определения напряжения
Для расчёта напряжения и сопротивления в цепи используются формулы или готовые онлайн калькуляторы.
Через силу тока и сопротивление
| Значение | Формула |
| Базовый расчёт напряжения на участке цепи | U=I/R, где I — сила тока в Амперах, а R — сопротивление в Омах |
| Определение напряжения в цепи переменного тока | U=I/Z, где Z — сопротивление в Омах, измеренное по всей протяженности цепи |
Закон Ома имеет исключения для применения:
- При прохождении токов высокой частоты происходит быстрое изменение электромагнитных полей. При расчёте высокочастотных цепей следует учитывать инерцию частиц, которые переносят заряд.
- При работе цепей в условиях низких температур (вблизи абсолютного нуля) у веществ может возникать свойство сверхпроводимости.
- Нагретый проходящими токами проводник является причиной возникновения переменного сопротивления.
- При нахождении под воздействием высокого напряжения проводников или диэлектриков.
- Во время процессов, проходящих в устройствах на основе полупроводников.
- При работе светодиодов.
Через мощность и силу тока
При известной мощности потребителей и силе тока напряжение высчитывается по формуле U=P/I, где P — мощность в Ваттах, а I — сила тока в Амперах.
При расчётах в цепях переменного тока используется формула иного вида: U=(P/I)*cosφ, где cosφ — коэффициент мощности, зависит от характера нагрузки.
При использовании приборов с активной нагрузкой (лампы накаливания, приборы с нагревательными спиралями и элементами) коэффициент приближается к единице. При расчётах учитывается возможность наличия реактивного компонента при работе устройств и значение cosφ считается равным 0,95. При использовании устройств с реактивной составляющей (электрические двигатели, трансформаторы) принято считать cosφ равным 0,8.
Для проверки расчётов рекомендуется сравнивать результат со стандартным напряжением, которое равняется 220 Вольт для однофазной сети и 380 Вольт — для трёхфазной.
Через работу и заряд
Методика расчёта используется в лабораторных задачах и на практике не применяется.
Формула имеет аналогичный закону Ома вид: U=A/q, где A — выполненная работа по перемещению заряда в Джоулях, а q — прошедший заряд, измеренный в Кулонах.
Расчёт сопротивления
При работе проводник создает препятствие течению электрического тока, которое называется сопротивлением. При электротехнических расчетах применяется понятие удельного сопротивления, которое измеряется в Ом*м.
| Значение | Формула |
| Расчет сопротивления одного элемента | R=U/I, где U — напряжение в Вольтах, а I — сила тока в Амперах |
| Расчет для однородного проводника | R=(ρ*l)/S, где ρ — значение удельного сопротивления (Ом*м, берётся из таблиц значений), l — длина отрезка проводника (метры), а S — площадь поперечного сечения (м2) |
Последовательное подключение
При последовательном соединении выход элемента связан со входом следующего. Общее сопротивление находится при помощи расчётной формулы: R=R1+R2+…+Rn, где R=R1+R2+…+Rn — значения сопротивления элементов в Омах.
Параллельное подключение
Параллельным называется соединение, при котором оба вывода одного элемента цепи соединены с соответствующими контактами другого. Для параллельного подключения характерно одинаковое напряжение на элементах. Ток на каждом элементе будет пропорционален сопротивлению.
Общее сопротивление высчитывается по формуле: 1/R=1/R1+1/R2+…+1/Rn.
В реальных схемах электропроводки применяется смешанное соединение. Для расчёта сопротивления следует упростить схему, просуммировав сопротивления в каждой последовательной цепи. Затем схему уменьшают путём расчёта отдельных участков параллельного соединения.
Смешанное соединение резисторов в цепи
В чистом виде параллельные и последовательные цепи в электротехнике встречаются крайне редко. Как правило, присутствует их совместная комбинация. Для того чтобы найти силу тока в каждом резисторе при смешанном соединении, необходимо цепь разбить на участки. Таким образом при расположении элементов друг после друга, т.н. «каскадом», применяются правила и формулы для последовательного соединения.
Результаты измерения силы тока в резисторе. Различные типы резисторов.
Необходимо отметить, что для упрощения расчетов параллельно расположенные резисторы можно группировать. При вычислении силы тока на определенном участке, они принимаются за самостоятельный элемент. Соответственно в этом случае формулы используются как для расчета параметров при параллельном соединении.
https://youtube.com/watch?v=DmGBdgME-7k
Калькулятор делителя напряжения
Разделитель напряжения представляет собой схему, используемую для создания напряжения, которое меньше или равно входному напряжению.
Выходное напряжение (V out )
Вольт (V)
Как найти выходное напряжение цепи делителя
Два делителя напряжения резистора являются одной из наиболее распространенных и полезных схем, используемых инженерами. Основная цель этой схемы заключается в уменьшении входного напряжения до более низкого значения в зависимости от отношения двух резисторов. Этот калькулятор помогает определить выходное напряжение схемы делителя с учетом входного (или источника) напряжения и значений резисторов
Обратите внимание на то, что выходное напряжение в реальных схемах может быть различным, поскольку резистор и сопротивление нагрузки (при подключении выходного напряжения) становятся факторами
Уравнение
$$ V_ {out} = V_ {in} * \ frac {R_ {2}} {R_ {1} + R_ {2}} $$
Где:
$$ V_ {out} $$ = Выходное напряжение. Это уменьшенное напряжение.
$$ V_ {in} $$ = Входное напряжение.
$$ R_ {1} $$ и $$ R_ {2} $$ = значения резистора. Отношение $$ \ frac {R_ {2}} {R_ {1} + R_ {2}} $$ определяет масштабный коэффициент.
Приложения
Поскольку делители напряжения довольно распространены, их можно найти в ряде приложений. Ниже приведены лишь некоторые из мест, где эта схема найдена.
потенциометры
Возможно, наиболее распространенной схемой делителя напряжения является то, что используется потенциометр, который является переменным резистором. Схематическое изображение потенциометра показано ниже:
«Горшок» обычно имеет три внешних контакта: два являются концами резистора, а один подключен к рычагу стеклоочистителя. Стеклоочиститель разрезает резистор пополам и перемещает его, регулируя соотношение между верхней половиной и нижней половиной резистора. Соедините два внешних выводы к напряжению (вход) и ссылку (земля) со средним (стеклоочистители штифтом) в качестве выходного контакта и вы сам делитель напряжения.
Уровневые сдвиги
Другая область, в которой используются делители напряжения, — это когда напряжение должно быть выровнено. Наиболее распространенным сценарием является взаимодействие сигналов между датчиком и микроконтроллером с двумя разными уровнями напряжения. Большинство микроконтроллеров работают при напряжении 5 В, в то время как некоторые датчики могут принимать только максимальное напряжение 3, 3 В. Естественно, вы хотите выровнять напряжение от микроконтроллера, чтобы избежать повреждения датчика. Пример схемы показан ниже:
Схема выше показывает схему делителя напряжения, включающую резистор 2 кОм и 1 кОм. Если напряжение от микроконтроллера составляет 5 В, то пониженное напряжение на датчик рассчитывается как:
$$ V_ {out} = 5 * \ frac {2k \ Omega} {2k \ Omega + 1k \ Omega} = 3.33 V $$
Этот уровень напряжения теперь безопасен для работы датчика
Обратите внимание, что эта схема работает только для выравнивания напряжений и не выравнивания
Ниже приведены некоторые другие комбинации резисторов, используемые для выравнивания часто встречающихся напряжений:
| Комбинация резисторов | использование |
| 4, 7 кОм и 6, 8 кОм | От 12 В до 5 В |
| 4, 7 кОм и 3, 9 кОм | 9V до 5V |
| 3, 6 кОм и 9, 1 кОм | От 12 В до 3, 3 В |
| 3, 3 кОм и 5, 7 кОм | От 9 В до 3, 3 В |
Чтение резистивного датчика
Многие датчики являются резистивными устройствами и большинством микроконтроллеров считывают напряжение, а не сопротивление. Таким образом, резистивный датчик обычно подключается в цепи делителя напряжения с резистором для взаимодействия с микроконтроллером. Пример установки показан ниже:
Термистор — это датчик, сопротивление которого изменяется пропорционально температуре. Скажем, что термистор имеет сопротивление комнатной температуре 350 Ом. Сопряженное сопротивление выбирается равным 350 Ом.
Когда термистор находится при комнатной температуре, выходное напряжение:
$$ V_ {out} = 5 * \ frac {350 \ Omega} {350 \ Omega + 350 \ Omega} = 2.5V $$
Когда температура увеличивается, сопротивление термистора изменяется до 350, 03 Ом, выход изменяется на:
$$ V_ {out} = 5 * \ frac {350.03 \ Omega} {350 \ Omega + 350.03 \ Omega} = 2.636V $$
Такое небольшое изменение напряжения обнаруживается микроконтроллером. Если функция передачи термистора известна, теперь можно рассчитать эквивалентную температуру.
Дальнейшее чтение
Техническая статья — Разделители напряжения и тока: что это такое и что они делают
Учебник — Глава 6 — Цепи Divider и законы Кирхгофа
Учебник — Потенциометр в качестве делителя напряжения
Рабочий лист — Цепь делителя напряжения
Расчет делителя напряжения на резисторах
Расчет делителя напряжения предполагает, что нам известно, по крайней мере, три величины из приведенной выше схемы: входное напряжение и сопротивление обоих резисторов. Зная эти величины, мы можем рассчитать выходное напряжение.
Формула делителя напряжения
Это не сложное упражнение, но очень важное для понимания того, как работает делитель напряжения. Расчет делителя основан на законе Ома
Для того чтобы узнать какое напряжение будет на выходе делителя, выведем формулу исходя из закона Ома. Предположим, что мы знаем значения Uin, R1 и R2. Теперь на основании этих данных выведем формулу для Uout. Давайте начнем с обозначения токов I1 и I2, которые протекают через резисторы R1 и R2 соответственно:
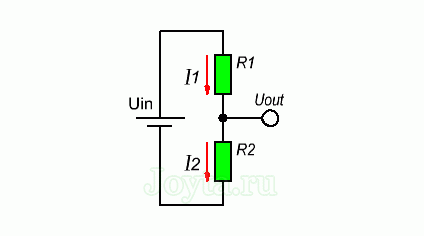
Наша цель состоит в том, чтобы вычислить Uout, а это достаточно просто используя закон Ома:
Хорошо. Мы знаем значение R2, но пока неизвестно сила тока I2. Но мы знаем кое-что о ней. Мы можем предположить, что I1 равно I2. При этом наша схема будет выглядеть следующим образом:
Что мы знаем о Uin? Ну, Uin это напряжение на обоих резисторах R1 и R2. Эти резисторы соединены последовательно, при этом их сопротивления суммируются:
И, на какое-то время, мы можем упростить схему:
Закон Ома в его наиболее простом вид: Uin = I *R. Помня, что R состоит из R1+R2, формула может быть записана в следующем виде:
А так как I1 равно I2, то:
Это уравнение показывает, что выходное напряжение прямо пропорционально входному напряжению и отношению сопротивлений R1 и R2.
Математический рассчет
Рассмотрим пример.
У нас есть аккумуляторная батарея с напряжением питания 12 Вольт. К ней напрямую подключен резистор (сопротивление) 10 Ом. Для того что бы рассчитать какая мощность приложена к нашему резистору, можно воспользоваться формулой.
P = E2/R
P = 122/10
P = 144/10.P = 14.4 wattsМощность рассеиваемая на резисторе состовляет 14,4 Ватта.
Если вы хотите определить величину тока протекающего через проводник, мы используем другую формулу
I = E/R
I = 12/10I = 1.2 ampsСила тока протекающего через цепь составляет 1,2 Ампера
—————-
Калькуляторы зависимости напряжения, силы тока и сопротивления.
ЭДС. Закон Ома для полной цепи
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи, то есть в проводниках, подсоединённых к клеммам источника тока.
Как мы знаем, положительный заряд :
• уходит во внешнюю цепь с положительной клеммы источника;
• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;
• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.
https://youtube.com/watch?v=5DpeGSiPwOg
Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной.
Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила , направленная против движения заряда (т.е.
против направления тока).
Сторонняя сила
Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).
Рис. 1. Сторонняя сила
Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила не имеет отношения к стационарному электрическому полю — у неё, как говорят, неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.
Обозначим через работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы называется также работой источника тока.
Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, — это также работа сторонней силы по перемещению заряда по всей цепи.
Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.
Опыт показывает, что работа прямо пропорциональна перемещаемому заряду . Поэтому отношение уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается :
(1)
Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.
Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.