Меню раздела
Цифровая электроникаЛогические элементыКомбинированные элементыАнализ схемТаблица истинности и цифровая схемаЛогические функции и цифровые схемыТребуемая функция и реальная функцияАлгебра логикиПеременные и постоянные величиныЗаконы алгебры логикиАксиомы и тождества алгебры логикиФункции «И-НЕ» и «ИЛИ-НЕ»Синтез схемНормальные формы записиУпрощение и преобразованиеМетод карт КарноРасчет логических схемЗадания по схемотехническому проектированиюСемейства схемБинарные уровни напряженияПоложительная и отрицательная логикаСвойства схемДТЛ-схемыМПЛ-схемыТТЛ-схемыСтандартные ТТЛ-схемыПредельные значения и параметры схемТТЛ с пониженным энергопотреблениемШотки-ТТЛ (ТТЛШ)ТТЛШ с пониженным энергопотреблениемСравнительная оценка логических элементовЭмиттерно-связанная логикаЛогические элементы на МОП-транзисторахЛогические элементы на р-канальных МОП-транзисторахЛогические элементы на л-канальных МОП-транзисторахЛогические элементы на КМОП-транзисторахЛогические элементы на МОП-транзисторахБинарные схемы с временной зависимостьюКлассификация триггеровНе тактируемые триггерыТриггер на элементах «И-НЕ»Тактируемые триггерыЯБ-триггеры с доминирующим Я-входомЕ-триггерD-триггерТриггеры, управляемые по фронту синхроимпульсаRS-триггеры, управляемые по одному фронтуT-триггеры, управляемые по одному фронтуJK-триггеры, управляемые по одному фронтуD-триггеры, управляемые по одному фронтуЯБ-триггеры, управляемые по обоим фронтамЖ-триггеры, управляемые по обоим фронтамДополнительные триггерные схемыВременные диаграммыХарактеристические уравненияМоностабильные ячейкиЭлементы задержки
Логическая схемы «НЕ» (инвертор)
Логическая схема НЕ имеет один вход и один выход. Моделью схемы может служить электрическая цепь (рис. 6, а) с размыкающим контактом реле Р.
Рис. 6. Схема НЕ (инвертор)
При срабатывании реле (сигнал 1 на входе) лампа не горит (сигнал 0 на выходе), при отпускании реле (сигнал 0 на входе) лампа горит (сигнал 1 на выходе). Таким образом, схема НЕ является инвертором, т. е. преобразователем сигнала одного вида в противоположный.
Инверторы собирают на транзисторах по схемам, представленным для положительной логики на рис. 6, б и для отрицательной — на рис. 6, в. При наличии на входе сигнала 0 меньше Есм транзистор закрыт и на выходе возникает сигнал 1. Если на входе сигнал 1 больше Есм, транзистор открыт и на выходе сигнал 0.
Тема 6. Логические устройства. Цифровые сигналы
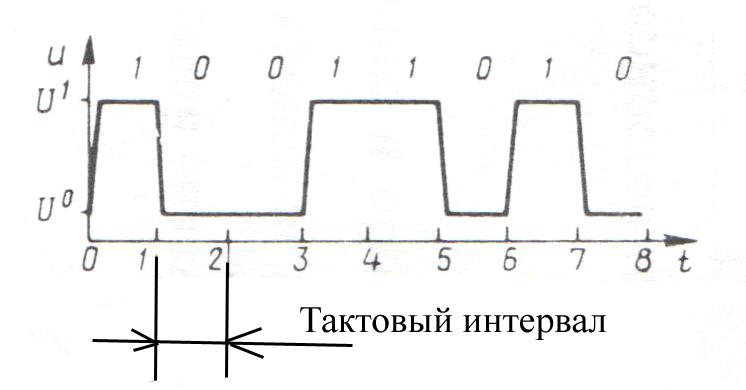
Цифровые устройства работают с цифровыми сигналами, которые могут принимать только два значения: от 0 до 0,5 В — уровень нуля или от 2,5 до 5 В — уровень единицы. В отличие от аналоговых, цифровые сигналы, имеющие только два разращенных значения, защищены от действия шумов, наводок и помех. Небольшие отклонения от разращенных значений не искажают цифровой сигнал, так как существуют зоны допустимых отклонений. Кроме того, цифровые устройства проще проектировать и отлаживать. Цифровым сигналом представляются двоичные числа, поэтому он состоит из элементов только двух различных значений. Одним из них представляется 1, а другим — 0. По установившейся терминологии эти элементы сигнала называют соответственно единицей и нулём. Цифровой сигнал может быть потенциальным или импульсным. Элементами потенциального цифрового сигнала являются потенциалы двух уровней. Каждый уровень остаётся неизменным в течении так называемого тактового интервала; на его границе уровень потенциала изменяется, если следующая цифра двоичного числа отличается от предыдущей. На рисунке изображён потенциальный цифровой сигнал, представляющий написанное сверху число; высоким потенциалом отображается 1, а низким — 0.
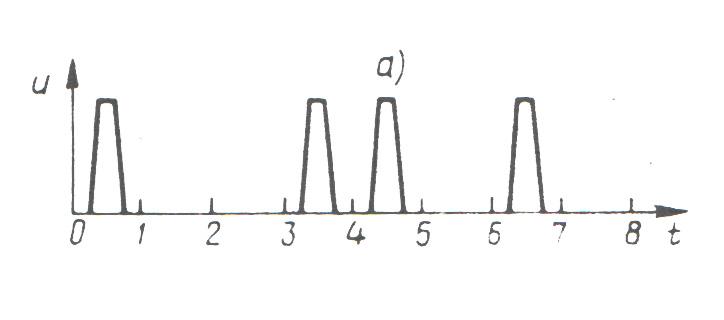
Элементами импульсного цифрового сигнала являются импульсы неизменной амплитуды и их отсутствие. На рисунке положительный импульс представляет 1, а отсутствие импульса представляет 0 написанного сверху двоичного числа.
3.12. Упражнения
3.1. Определите с помощью таблиц истинности, какие из следующих
формул являются тождественно истинными или тождественно ложными:
| а) | e) |
| b) | f) |
| c) | g) |
| d) |
3.2. Упростите следующие формулы, используя законы склеивания:
- а)
- b)
- c)
- d)
- e) Решение: .
3.3. Упростите следующие формулы, используя законы поглощения:
- а)
- b)
- c)
- d)
3.4. Постройте таблицы истинности для логических формул и упростите
формулы, используя законы алгебры логики:
- а)
- b)
- c)
- d)
- e)
- f)
- g)
- h)
- i)
3.5. Приведите примеры переключательных схем, содержащих хотя бы два
переключателя, функция проводимости которых
- а) тождественно равна единице;
- b) тождественно равна нулю.
3.6. Найдите функции проводимости следующих переключательных схем:
| а) | b) | ||
| c) | d) |
3.7. Проверьте равносильность следующих переключательных схем:
- а)
- b)
- c)
- d)
- e)
3.8. Постройте переключательные схемы с заданными функциями
проводимости:
3.9. Упростите функции проводимости и постройте переключательные
схемы, соответствующие упрощенным функциям:
а)b)c)d)e)f)g)h)i)
3.10. Упростите следующие переключательные схемы:
- а)
- b)
- c)
- d)
Элемент ИЛИ-НЕ
Здесь все по аналогии с элементом И-НЕ. Операция, выполняемая элементом ИЛИ-НЕ называется инверсией логического сложения или инверсией дизъюнкции и еще красивым словосочетанием стрелка Пирса. Стрелка потому, что в виде формулы функция записывается так: y = x 1↓ x2. Символ между иксами и есть стрелка какого-то Пирса.
Обозначается элемент ИЛИ-НЕ вот так:
Таблица истинности:
| x2 | x1 | y |
| 1 | ||
| 1 | ||
| 1 | ||
| 1 | 1 |
Аналогично, если к выходу элемента ИЛИ-НЕ прилепить инвертор, то получится элемент ИЛИ.
Существуют еще различные логические элементы но практически все они сделаны на основе боле простых, которые мы как раз и рассмотрели.Остальные элементы мы будем разбирать уже по ходу дела, а здесь, пожалуй, стоит уделить внимание еще одному элементу который называется
Логические основы работы компьютера
Знания из области математической логики можно использовать для конструирования электронных устройств. Нам известно, что 0 и 1 в логике не просто цифры, а обозначение состояний какого-то предмета нашего мира, условно называемых «ложь» и «истина». Таким предметом, имеющим два фиксированных состояния, может быть электрический ток.
Логические элементы имеют один или несколько входов и один выход, через которые проходят электрические сигналы, обозначаемые условно 0, если «отсутствует» электрический сигнал, и 1, если «имеется» электрический сигнал.
Базовые логические элементы реализуют три основные логические операции: «И», «ИЛИ», «НЕ».
Логический элемент «НЕ» (инвертор)
Простейшим логическим элементом является инвертор, выполняющий функцию отрицания. Если на вход поступает сигнал, соответствующий 1, то на выходе будет 0. И наоборот.
У этого элемента один вход и один выход. На функциональных схемах он обозначается:
Говорят также, что элемент «НЕ» инвертирует значение входной двоичной переменной.
Проверь соответствие логического элемента «НЕ» логическому элементу «НЕ». Воспользуйся тренажером Логические элементы.xlsx
Логический элемент «И» (конъюнктор)
Логический элемент «И» (конъюнктор) выдает на выходе значение логического произведения входных сигналов.
Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:
Сигнал на выходе конъюнктора появляется тогда и только тогда, когда поданы сигналы на все входы. На элементарном уровне конъюнкцию можно представить себе в виде последовательно соединенных выключателей. Известным примером последовательного соединения проводников является елочная гирлянда: она горит, когда все лампочки исправны. Если же хотя бы одна из лампочек перегорела, то гирлянда не работает.
Проверь соответствие логического элемента «И» логическому элементу «И». Воспользуйся тренажером Логические элементы.xlsx
Логический элемент «ИЛИ» (дизъюнктор)
Логический элемент «ИЛИ» (дизъюнктор) выдает на выходе значение логической суммы входных сигналов. Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:
Сигнал на выходе дизъюнктора не появляется тогда и только тогда, когда на все входы не поданы сигналы.
На элементарном уровне дизъюнкцию можно представить себе в виде параллельно соединенных выключателей.
Примером параллельного соединения проводников является многорожковая люстра: она не работает только в том случае, если перегорели все лампочки сразу.
Проверь соответствие логического элемента «ИЛИ» логическому элементу «ИЛИ». Воспользуйся тренажером Логические элементы.xlsx
Пример 1.Составьте логическую схему для логического выражения: F=A \/ B /\ A.
1.Две переменные – А и В.
2.Две логические операции: 1-/\, 2-\/.
3.Строим схему:
Пример 2.Постройте логическую схему, соответствующую логическому выражению F=А/\В\/ ¬(В\/А). Вычислить значения выражения для А=1,В=0.
1.Переменных две: А и В; 1 4 3 2
2.Логических операций три: /\ и две \/; А/\В\/ ¬ (В\/ А).
3.Схему строим слева направо в соответствии с порядком логических операций:
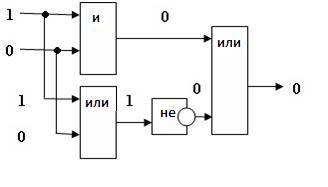
4. Вычислим значение выражения: F=1 /\ 0 \/ ¬(0 \/ 1)=0
Уровни проектирования
- топологический — топологические фотошаблоны для производства
- физический — методы реализации одного транзистора (или небольшой группы) в виде легированных зон на кристалле
- электрический — принципиальная электрическая схема (транзисторы, конденсаторы, резисторы и т. п.)
- схемо- и системотехнический уровень — схемо- и системотехнические схемы (триггеры, компараторы, шифраторы, дешифраторы, АЛУ и т. п.)
- логический — логическая схема (логические инверторы, элементы ИЛИ-НЕ, И-НЕ и т. п.)
- программный — позволяет программисту программировать (для ПЛИС, микроконтроллеров и микропроцессоров) разрабатываемую модель, используя виртуальную схему
В настоящее время (2014 г.) большая часть интегральных схем проектируется при помощи специализированных САПР, которые позволяют автоматизировать и значительно ускорить производственные процессы, например, получение топологических фотошаблонов.
INFO
Тут стоит упомянуть, что с теми же целями мы можем использовать и 74HC00N (четыре элемента NAND). Эта микросхема получила свой особый «нулевой» номер в серии 74хх не просто так — логическая операция И — НЕ обладает замечательным свойством функциональной полноты. Иными словами, мы можем любой другой базовый блок (AND, OR и остальные) разложить на комбинацию блоков NAND. Аналог в отечественной микроэлектронике — 155ЛА3, и это настолько популярная у радиолюбителей микросхема, что в ее честь даже называют сайты. Простой пример (как на картинке выше) позволяет на практике убедиться, что микросхема работает, как мы предполагали. Для мигания светодиодами и переключения состояний в такой ячейке памяти достаточно прикасаться концами проводов (от земли или питания) к соответствующим выводам микросхемы. Возможно, само по себе это звучит и не очень увлекательно, но размышление в процессе должно навести на интересные идеи.
Некоторая неопределенность
В какой-то момент твой пытливый хакерский ум наверняка задался вопросом — а что, если подать одно и то же напряжение на обе половинки одновременно? И в каком состоянии окажется наша схема после? В сущности, это сродни делению на ноль в математике (или программировании) — запрещенная операция, результат на выходе которой не определен. Парадоксально, но даже такое свойство может иметь практическое применение! Инженеры в Intel хорошо знают схемотехнику (кто бы сомневался), и встроенный в их процессоры генератор случайных чисел работает именно по такому принципу.
Сейчас работа нашей схемы напоминает электромеханические компьютеры середины сороковых годов XX века, когда коммутация сигналов внутри устройства выполнялась с помощью реле и переключателей. Самое время добавить новые возможности и перейти от инверторов к элементам с несколькими входами.
Логические схемы «ИЛИ» на диодах
Моделью схемы ИЛИ может служить цепь, изображенная на рис. 4, а. Лампа загорится, если замкнуты контакты Р1, «ИЛИ» Р2, «ИЛИ» Р3.
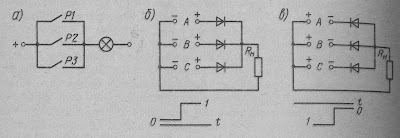
Рис. 4. Схема ИЛИ на диодах
На выходе схемы ИЛИ возникает сигнал 1, если такой же сигнал подан на один или несколько входов. Схема ИЛИ является схемой сборки (информации); по какому бы каналу ни пришел сигнал 1, он появляется на выходе. Схема ИЛИ осуществляет логическое сложение, что подтверждается выражением:
Действительно, у = 0 при х1 = х2 = … = хn = 0; у = 1, если на одном входе возникает сигнал 1, а на всех других — сигнал 0; у = 1 при х1 = х2 = … = xn = 1 (следует помнить, что у и х могут иметь только два значения 1 или 0). Логическое сложение носит название дизъюнкции, поэтому схему можно назвать дизъюнктором.
Схема ИЛИ может быть собрана на диодах в варианте для положительной логики (Рис. 4, б) и для отрицательной логики (рис. 4, в). Принципы действия этих схем и логических схем И на диодах ничем не отличаются. При перемене уровня сигналов 1 и 0 схема ИЛИ может выполнять функции схемы И.
В словаре Синонимы 4
азот, актиний, алюминий, америций, аргон, астат, барий, бериллий, берклий, биоэлемент, бор, бром, бронеэлемент, висмут, водород, вольфрам, гадолиний, галлий, гафний, гелий, германий, гольмий, диспрозий, доля, европий, железо, жолиокюрий, звено, золото, индий, иод, иридий, иттербий, иттрий, кадмий, калий, калифорний, кальций, кислород, кобальт, компонент, кремний, криптон, ксенон, курчатовий, кюрий, лантан, литий, лоуренсий, лютеций, магний, макроэлемент, марганец, медь, менделевий, метеоэлемент, микроэлемент, молибден, мышьяк, натрий, начало, неодим, неон, нептуний, никель, нильсборий, ниобий, нобелий, олово, осмий, палладий, платина, плутоний, пневмоэлемент, полоний, празеодим, прометий, протактиний, радий, радиоэлемент, радон, резерфордий, рений, родий, ртуть, рубидий, рутений, самарий, свинец, селен, сера, серебро, скандий, стронций, сурьма, таллий, тантал, твэл, теллур, тербий, термопара, термоэлемент, технеций, титан, торий, тулий, углерод, ультраэлемент, уран, фермий, фильтроэлемент, фосфор, франций, фтор, хлор, хром, цезий, цельсий, церий, цинк, цирконий, часть, эйнштейний, электрорадиоэлемент, электроэлемент, эрбий
Примеры
Диаграмма Хассе примера 2
- Подмножество целых чисел не имеет верхней границы в наборе из действительных чисел .р{\ Displaystyle \ mathbb {R}}
- Пусть отношение на задана Множество имеет верхние пределы и , но не верхняя не связывало и не наибольший элемент (см рисунок).≤{\ Displaystyle \, \ Leq \,}{а,б,c,d}{\ Displaystyle \ {а, б, в, г \}}а≤c,{\ displaystyle a \ leq c,} а≤d,{\ displaystyle a \ leq d,} б≤c,{\ displaystyle b \ leq c,} б≤d.{\ displaystyle b \ leq d.}{а,б}{\ Displaystyle \ {а, б \}}c{\ displaystyle c}d,{\ displaystyle d,}
- В рациональных числах множество чисел с квадратом меньше 2 имеет верхнюю границу, но не имеет наибольшего элемента и наименьшей верхней границы.
- В наборе чисел меньше 1 есть наименьшая верхняя граница, а именно. 1, но не самый большой элемент.р,{\ displaystyle \ mathbb {R},}
- В наборе чисел, меньших или равных 1, есть наибольший элемент, а именно. 1, что также является его точной верхней границей.р,{\ displaystyle \ mathbb {R},}
- В с того продукта , множество пар с не имеет верхней границы.р2{\ Displaystyle \ mathbb {R} ^ {2}}(Икс,у){\ Displaystyle (х, у)}<Икс<1{\ Displaystyle 0 <х <1}
- В соответствии с лексикографическим порядком это множество имеет верхнюю границу , например, не имеет наименьшей верхней границы.р2{\ Displaystyle \ mathbb {R} ^ {2}}(1,).{\ displaystyle (1,0).}
Примечания
- (недоступная ссылка). Дата обращения: 11 октября 2010.
- . Chip News №8, 2000 г..
- .
- История отечественной электроники, 2012 г., том 1, под ред. директора Департамента радиоэлектронной промышленности Минпромторга России Якунина А. С., стр. 632
- Охраняется гл. 74 «Право на топологии интегральных микросхем» ГК РФ как интеллектуальная собственность ().
- ↑
- Нефедов А.В., Савченко A.M., Феоктистов Ю.Ф. Зарубежные интегральные микросхемы для промышленной электронной аппаратуры: Справочник. — М.: Энергоатомиздат, 1989. — С. 4. — 300 000 экз. — ISBN 5-283-01540-8.
- Якубовский С.В., Барканов Н.А., Ниссельсон Л.И. Аналоговые и цифровые интегральные микросхемы. Справочное пособие. — 2-е изд. — М.: «Радио и связь», 1985. — С. 4—5.
Основные ворота
В предыдущих главах мы узнали, что булевы функции могут быть представлены либо в форме суммы произведений, либо в форме произведения сумм в зависимости от требования. Таким образом, мы можем реализовать эти булевы функции, используя базовые элементы. Основными воротами являются И, ИЛИ И НЕ ворота.
И ворота
Логический
элемент И представляет собой цифровую схему, которая имеет два или более входов и производит выход, который являетсялогическим И всех этих входов.Логическое И необязательно обозначать символом «.».
В следующей таблице показана таблица истинности
2-входного логического элемента AND.
| В | Y = AB | |
| 1 | ||
| 1 | ||
| 1 | 1 | 1 |
Здесь A, B — входы, а Y — выход двух входных И логических элементов. Если оба входа «1», то только выход, Y «1». Для оставшихся комбинаций входов выход Y равен 0.
На следующем рисунке показан символ
логического элемента AND, который имеет два входа A, B и один выход Y.
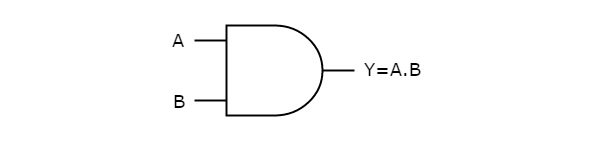
Этот логический элемент И производит выход (Y), который является логическим И
двух входов А, В. Аналогичным образом, если есть ‘n’ входов, то логический элемент И производит выход, который является логическим И всех этих входов. Это означает, что выход логического элемента AND будет равен «1», когда все входы равны «1».
ИЛИ ворота
Логический элемент ИЛИ — это цифровая схема, которая имеет два или более входов и создает выход, который является логическим ИЛИ всех этих входов. Это логическое ИЛИ
обозначается символом «+».
В следующей таблице показана таблица истинности
2-входного ИЛИ вентиля.
| В | Y = A + B | |
| 1 | 1 | |
| 1 | 1 | |
| 1 | 1 | 1 |
Здесь A, B — входы, а Y — выход двух входных логических элементов ИЛИ. Если оба входа «0», то только выход, Y «0». Для остальных комбинаций входов выход Y равен «1».
На следующем рисунке показан символ
логического элемента ИЛИ, который имеет два входа A, B и один выход Y.
Этот логический элемент ИЛИ выдает выход (Y), который является логическим ИЛИ
двух входов A, B. Аналогично, если имеется ‘n’ входов, то вентиль ИЛИ генерирует выход, который является логическим ИЛИ всех этих входов. Это означает, что выход логического элемента ИЛИ будет равен «1», когда хотя бы один из этих входов равен «1».
НЕ ворота
Логический элемент NOT — это цифровая схема с одним входом и одним выходом. Выход NOT gate является логической инверсией
ввода. Следовательно, вентиль НЕ также называется инвертором.
В следующей таблице показана таблица истинности
NOT gate.
| Y = A ‘ |
| 1 |
| 1 |
Здесь A и Y — вход и выход элемента НЕ соответственно. Если вход A равен 0, то выход Y равен 1. Точно так же, если вход A равен «1», то выход Y равен «0».
На следующем рисунке показан символ
НЕ, который имеет один вход A и один выход Y.
Этот НЕ вентиль производит вывод (Y), который является дополнением
ввода, A.
Правовая защита
Законодательство России предоставляет правовую охрану топологиям интегральных микросхем. Топологией интегральной микросхемы является зафиксированное на материальном носителе пространственно-геометрическое расположение совокупности элементов интегральной микросхемы и связей между ними (ст. 1448 ГК РФ).
Автору топологии интегральной микросхемы принадлежат следующие интеллектуальные права:
- исключительное право;
- право авторства.
Автору топологии интегральной микросхемы принадлежат также другие права, в том числе право на вознаграждение за использование служебной топологии.
Исключительное право на топологию действует в течение десяти лет. Правообладатель в течение этого срока может по своему желанию зарегистрировать топологию в Федеральной службе по интеллектуальной собственности, патентам и товарным знакам.
Логические схемы «И» на транзисторах
Логические схемы И могут быть собраны на транзисторах (рис. 3). В схеме И для положительной логики используются транзисторы типа n — p — n (рис. 3, а). При наличии сигнала 0 на одном из входов соответствующий транзистор закрыт напряжением смещения Есм, так как напряжение сигнала 0 ниже Есм. Второй транзистор может быть открыт при сигнале на входе 1 (напряжение сигнала 1 выше Есм). Переход эмиттер — коллектор закрытого транзистора практически обрывает цепь питания, и на выходе возникает сигнал 0.
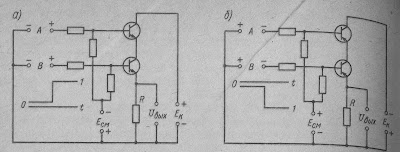
Рис. 3. Схема И на транзисторах
Когда на входах появляются сигналы 1, оба транзистора открыты и на выходе возникает сигнал 1. В схеме И для отрицательной логики (рис. 3, б) используются транзисторы типа р — n — р. Принципы работы данной и предыдущей схем аналогичны, однако полярность сигналов, смещения и питания обратная.
Основные элементы страницы сайта
Итак, давайте перечислим главные элементы страницы сайта, разберем, что они собой представляют и каким обладают функционалом.
-
Шапка
Шапка (header) – это верхняя часть страницы. Как правило, без нее не обходятся, создавая интернет-ресурс. Хотя иногда шапку и не используют.
-
Top-Line Branding
В этой части страницы находится информация о компании, иногда здесь также размещается суббренд или перечисляются теги. Место логотипа, как правило, в углу слева, хотя такое расположение не является обязательным – просто к этому привыкло большинство интернет-пользователей.
-
Основная система навигации
В основном система навигации привязана к шапке сайта. Отсюда можно добраться до всех его разделов. Если ресурс не имеет множества страниц, вполне нормально разместить в шапке выпадающее меню, в котором будет полная навигация.
-
Вспомогательная система навигации
Довольно часто на сайтах имеется еще одна система навигации, она включает элементы, которые не играют большой роли в процессе продаж. К ним могут относиться разделы «О нас» и «Контакты».
-
Поиск
Специальное поле для поисковых запросов обычно тоже помещают в шапке, что является вполне закономерным решением, учитывая соседство с системой навигации.
-
Учетная запись и авторизация
В шапке обычно размещается и поле для регистрации/авторизации, если на сайте в принципе имеется возможность создать безопасный личный кабинет.
-
Навигация/Меню
Выше уже упоминалось о системе навигации как части шапки сайта. Однако такая система по себе является самостоятельным элементом страницы. Главным образом есть три основные системы навигации на основе меню. Другие существующие варианты вторичны.
Подробнее
-
Вкладки
Вкладки нужны, чтобы перемещаться по разделам сайта. Своей системы навигации во вкладках нет, перенаправление происходит средствами связанных с вкладками страниц.
-
Выпадающие меню
Подобное меню бывает вертикальным и горизонтальным, обычно используется второй вариант. Довольно часто выпадающее меню используется на различных сайтах. Интуитивно оно понятно пользователям из-за своего широкого распространения и удобства. Этот вариант меню позволяет быстро оказаться в нужном разделе сайта, не проделывая длительный путь. Иногда разработчики конструируют настраиваемые выпадающие меню, так как сайт содержит большое количество параметров.
-
Древовидное меню
Древовидное меню, как правило, является вертикальным и помещается сбоку страницы. Оно может содержать ссылки на все разделы сайта либо на подразделы текущих страниц. Такое меню бывает статичным или разворачивается при клике/наведении курсора на него.
Пожалуй, стандартные способы отображения контента – самые простые, понятные и доступные новичкам.
-
Нижний колонтитул
Нижние колонтитулы (footers) в основном используют либо как полезную площадь сайта, куда помещают инструменты навигации, имеющие реальные функции, либо как место для информации, которая должна быть на сайте, но при этом не имеет большого значения для пользователей. Зачастую нижний колонтитул особенно не используется, и постепенно туда «сбрасывается» все ненужное. Это нормальное явление, и не имеет смысла переживать об этом.
Однако часто нижний колонтитул становится местом, где размещаются элементы навигационной системы. И в этом есть смысл: если пользователь заинтересован предложениями компании и прокрутил весь сайт вниз, разумно будет показать ему путь к нужному контенту.
Что можно найти в нижнем колонтитуле:
- сведения об авторских правах и ссылки на правовую информацию, например, политику конфиденциальности;
- копию основной системы навигации сайта;
- полную или частичную карту сайта;
- ссылки на контент, который интересен только узкой части пользователей, к примеру, информация о сотрудничестве с компанией, размещении рекламы и т.п.
Нередко в этой области располагают карту сайта, которая дает пользователям возможность без труда ориентироваться на площадке. Предоставление подобной информации куда полезнее пустых колонтитулов. Зачастую нижняя часть сайта становится довольно объемной за счет большого количества данных. Кроме того, в нижний колонтитул можно поместить динамический контент (последние комментарии или отзывы клиентов). Это оживляет интернет-площадку, располагает к тому, чтобы задержаться на ней.
3.1.Простейшие логические элементы
Изучение базовых элементов цифровой электроники начнем с наиболее простых, а затем будем рассматривать все более сложные. Примеры применения каждого следующего элемента будут опираться на все элементы, рассмотренные ранее. Таким образом, будут постепенно даны главные принципы построения довольно сложных цифровых устройств.
Логические элементы (или, как их еще называют, вентили, «gates») — это наиболее простые цифровые микросхемы. Именно в этой простоте и состоит их отличие от других микросхем. Как правило, в одном корпусе микросхемы может располагаться от одного до шести одинаковых логических элементов. Иногда в одном корпусе могут располагаться и разные логические элементы.
Обычно каждый логический элемент имеет несколько входов (от одного до двенадцати) и один выход. Все входы равноправны. При этом связь между выходным сигналом и входными сигналами (таблица истинности) предельно проста. Каждой комбинации входных сигналов элемента соответствует уровень нуля или единицы на его выходе. Никакой внутренней памяти у логических элементов нет, поэтому они относятся к группе так называемых комбинационных микросхем. Но в отличие от более сложных комбинационных микросхем, рассматриваемых в дальнейшем, логические элементы имеют входы, которые не могут быть разделены на группы, различающиеся по выполняемым ими функциям.
Главные достоинства логических элементов, по сравнению с другими цифровыми микросхемами, — это их высокое быстродействие (малые времена задержек), а также малая потребляемая мощность (малый ток потребления). Поэтому в тех случаях, когда требуемую функцию можно реализовать исключительно на логических элементах, всегда имеет смысл проанализировать этот вариант. Недостаток же их состоит в том, что на их основе довольно трудно реализовать сколько-нибудь сложные функции. Поэтому чаще всего логические элементы используются только в качестве дополнения к более сложным, к более «умным» микросхемам. И любой разработчик обычно стремится использовать их как можно меньше и как можно реже. Существует даже мнение, что мастерство разработчика обратно пропорционально количеству используемых им логических элементов. Однако это верно далеко не всегда.
3.4. Что такое логический элемент компьютера
|
Логический элемент компьютера — это часть электронной логичеcкой схемы, которая реализует элементарную логическую функцию. |
Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ,
И—НЕ, ИЛИ—НЕ и другие (называемые также вентилями), а также
триггер.
С помощью этих схем можно реализовать любую логическую функцию, описывающую
работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и
один или два выхода.
Чтобы представить два логических состояния — “1” и “0” в вентилях,
соответствующие им входные и выходные сигналы имеют один из двух установленных
уровней напряжения. Например, +5 вольт и 0 вольт.
Высокий уровень обычно соответствует значению “истина” (“1”), а низкий —
значению “ложь” (“0”).
Каждый логический элемент имеет свое условное обозначение, которое
выражает его логическую функцию, но не указывает на то, какая именно электронная
схема в нем реализована. Это упрощает запись и понимание сложных логических
схем.
Работу логических элементов описывают с помощью таблиц истинности.
|
Таблица истинности это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний. |
Элемент И-НЕ
И-НЕ — это схема И и схема НЕ, сложенные вместе. Операция, которую производит такой элемент называется инверсией логического умножения или отрицанием логического умножения, ну или инверсией конъюнкции и еще красивым словосочетанием штрих Шеффера. Штрих кого-то там называется потому, что в виде формулы операция И-НЕ записывается так: y = x1 | x2. Вертикальная черта между иксами и есть штрих какого-то Шеффера.
Логический элемент И-НЕ обозначается так:
Таблица истинности для него:
| x2 | x1 | y |
| 1 | ||
| 1 | 1 | |
| 1 | 1 | |
| 1 | 1 |
Ну то есть в принципе тут все просто: чуть выше мы рассматривали логический элемент И, а тут не его выходе прилеплен инвертор и поэтому все показания будут «наизнанку»
Логические схемы «ИЛИ» на транзисторах
На рис. 5, а приведена схема ИЛИ на транзисторах для положительной логики. Схема имеет два входа А и В и один выход.
Рис. 5. Схема ИЛИ на транзисторах
Транзисторы типа n — p — n соединены параллельно и играют роль ключей. При наличии на входе сигнала 0 соответствующий транзистор закрыт напряжением смещения Есм; если на второй вход подан сигнал 1 с напряжением больше, чем Есм, то второй транзистор открыт и на выходе возникает сигнал 1. Схема ИЛИ для отрицательной логики (рис. 5, б) построена по такому же принципу, однако используются транзисторы типа р — n — р и изменена полярность сигналов и напряжений смещения и питания.
Логические выражения и таблица истинности
Примеры задач с решениями по этой теме Пройти тестирование по теме Контрольная по теме
Таблица истинности — таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний.
Логическое выражение — составные высказывания в виде формулы.
Равносильные логические выражения – логические выражения, у которых последние столбцы таблиц истинности совпадают. Для обозначения равносильности используется знак «=».
Алгоритм построения таблицы истинности:
1.подсчитать количество переменных n в логическом выражении;
2. определить число строк в таблице по формуле m=2n, где n — количество переменных;
3. подсчитать количество логических операций в формуле;
4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;
5. определить количество столбцов: число переменных + число операций;
6. выписать наборы входных переменных;
7. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.
Заполнение таблицы:
1.разделить колонку значений первой переменной пополам и заполнить верхнюю часть «0», а нижнюю «1»;
2.разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;
3.продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.
Пример 1. Для формулы A/\ (B \/ ¬B /\¬C) постройте таблицу истинности.
Количество логических переменных 3, следовательно, количество строк — 23 = 8.
Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов — 3 + 5 = 8.
Пример 2. Определите истинность логического выражения F(А, В) = (А\/ В)/\(¬А\/¬В) .
1. В выражении две переменные А и В (n=2).
2. mстрок=2n, m=22=4 строки.
3. В формуле 5 логических операций.
4. Расставляем порядок действий
1) А\/ В; 2) ¬А; 3) ¬В; 4) ¬А\/¬В; 5) (А\/ В)/\(¬А\/¬В).
5. Кстолбцов=n+5=2+5=7 столбцов.
|
А |
В |
А\/ В |
¬А |
¬В |
¬А\/¬В |
F |
|
1 |
1 |
1 |
||||
|
1 |
1 |
1 |
1 |
1 |
||
|
1 |
1 |
1 |
1 |
1 |
||
|
1 |
1 |
1 |
Вывод: логическое выражение принимает значение истина при наборах F(0,1)=1 и F(1,0)=1.
Пример 3. Построёте таблицу истинности для логического выражения
F = (A\/ B) /\ ¬С
- В данной функции три логические переменные – А, В, С
- количество строк таблицы = 23 =8
- В формуле 3 логические операции.
- Расставляем порядок действий
1) А\/ В; 2) ¬С; 3) (AVB) /\ ¬С .
- количество столбцов таблицы = 3 + 3 = 6
|
А |
В |
С |
A\/B |
¬С |
(A\/B) /\ ¬С |
|
1 |
|||||
|
1 |
|||||
|
1 |
1 |
1 |
1 |
||
|
1 |
1 |
1 |
|||
|
1 |
1 |
1 |
1 |
||
|
1 |
1 |
1 |
|||
|
1 |
1 |
1 |
1 |
1 |
|
|
1 |
1 |
1 |
1 |
Пример 4. Определите истинность формулы: F = ((С \/В) => В) /\ (А /\ В) => В.
Построим таблицу истинности этой формулы.
Ответ: формула является тождественно истинной.
Пример 5. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
|
X |
Y |
Z |
F |
|
1 |
|||
|
1 |
|||
|
1 |
1 |
Какое выражение соответствует F?
1) ¬X/\¬Y/\Z 2) ¬X\/¬Y\/Z 3) X\/Y\/¬Z 4) X\/Y\/Z
Решение (вариант 1, через таблицы истинности):
Чтобы решить данную задачу можно построить часть таблицы истинности для каждой из четырех функций, заданных в ответе для заданных наборов входных переменных, и сравнить полученные таблицы с исходной:
|
X |
Y |
Z |
F |
¬X |
¬Y |
¬Z |
¬X/\¬Y/\Z |
¬X\/¬Y\/Z |
X\/Y\/¬Z |
X\/Y\/Z |
|
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Очевидно, что значения заданной функции F совпадают со значениями выражения X\/Y\/¬Z. Следовательно, правильный ответ – 3.
Ответ: 3
Решение (Вариант 2):
Чтобы не строить таблицу истинности для каждого выражения, можно просто перепроверить предложенные ответы по заданной таблице истинности. Т.е. в каждую из четырех предложенных функций последовательно подставлять значения переменных X, Y и Z, из заданной таблицы истинности и вычислять значения логического выражения. Если значения вычисляемого выражения совпадут со значением F во всех трех строчках заданной таблицы, то это и есть искомое выражение.
Рассмотрим данный конкретный пример:
1)первое заданное выражение ¬X/\¬Y/\Z = 0 при X=0, Y=0, Z=0, что не соответствует первой строке таблицы;
2)второе заданное выражение ¬X\/¬Y\/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы;
3)третье выражение X\/Y\/¬Z соответствует F при всех предложенных комбинациях X,Y и Z;
4)четвертое выражение X\/Y\/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы.
Ответ: 3
Логический элемент НЕ
Логический элемент «НЕ», который иначе называется инвертор, обозначается так:
Таблица истинности:
| x | y |
| 1 | |
| 1 |
Как видно, этот элемент проще всех. О том, что это инвертор, говорит кружок на выходе элемента. В электронике принято кружком обозначать инверсию сигнала, т. е. переворот фазы на 180 градусов. Вспомните операционный усилитель (ОУ), неинвертирующий вход как обычно, инвертирующий с кружком, т. к. на выходе ОУ при подаче сигнала на инвертирующий вход сигнал переворачивается по фазе на 180 градусов, т. е. инвертируется.
Теперь поглядим еще на парочку элементов, имеющих некоторые особенности.
Базисные элементы логики
Очевидно, базис происходит от слова «база». Абсолютно в дырочку. Намек понятен?Базисом называется совокупность элементов, с помощью которых схемотехнически можно реализовать устройство любой сложности. Простым языком, базис — это те элементы, при помощи которых можно сделать любое устройство (речь идет о цифровой технике). Да да, абсолютно любое и самое интересное, что этих базисных элементов всего 2. На их основе можно сделать все вышеперечисленные элементы и еще кучу других, что, собственно, и делается.