Расчет параллельного соединения резисторов
Последовательное и параллельное соединение аккумуляторов
Для лучшего понимания процессов следует подробно рассмотреть представленную ниже схему. В контрольных точках (разрывах цепей) условно показаны измерительные приборы. Аналогичным образом подключают мультиметр для уточнения результатов теоретических вычислений. Чтобы не усложнять объяснение, использован «идеальный» источник постоянного тока. Его сопротивление в расчетах не учитывается. Аналогичным образом игнорированы емкостные (индуктивные) реактивные составляющие, которые способны создать незначительные нелинейные искажения.
Электрическая схема с пояснительными формулами
В рассматриваемом примере ток (I) идет по замкнутому контуру от положительного к отрицательному электроду АКБ. На входе параллельного участка (точка «а») он разделяется на I1 (I2), проходящие через разные ветки с электрическими сопротивлениями R1 (R2), соответственно. В точке «б» происходит объединение токов.
Если присоединить клеммы мультиметра к положительной клемме аккумулятора и входной точке, а после повторить измерение на выходе, будут определены одинаковые значения. Однако в отдельных ветвях токи будут отличаться, если применены разные сопротивления (R1≠R2). Сложение показаний подтвердит равенство суммы полученным ранее результатам измерений на входе (выходе). Промежуточный вывод, подтвержденный экспериментально:
Iобщ = I1 + I2.
Далее можно проверить разницу потенциалов на клеммах источника питания (Uип), в контрольных точках (Uаб) и на отдельных резисторах (UR1 и UR2). Несложно убедиться в том, что Uип = Uаб = UR1 = UR2. Для отдельных ветвей будут действительны пропорции:
- UR1 = I1 * R1;
- UR2 = I2 * R2.
Однако с учетом результатов измерений можно приравнять обе стороны выражений:
UR1 = UR2 = I1 * R1 = I2 * R2.
Простым преобразованием получают соотношение:
I1/I2 = R2/R1.
На основе этой формулы надо сделать следующий важный вывод: токи обратно пропорциональны электрическим сопротивлениям в соответствующих ветвях параллельной цепи.
Пример с исходными данными:
- батарейка Uип = 6V;
- сопротивление параллельных резисторов: R1 = 50 Ом, R2 = 150 Ом.
Расчет:
- найти ток в первой ветке можно по формуле: I1 = Uип / R1 = 6/50 = 0,12А = 120 мА;
- аналогичным образом вычисляют: I2 = Uип / R2 = 6/150 = 0,04А = 40 мА;
- суммарное значение: Iобщ = I1 + I2 = 120 + 40 = 160 мА;
- соблюдается отмеченный выше принцип пропорциональности: I1/I2 = R2/R1 = 50/150 = 40/120 ≈ 0,333.
Следует отметить разную силу тока в отдельных ветках. Для наглядности можно вспомнить пример с аналогом из водопроводных труб. В разветвленном участке по протоку с крупным диаметром пройдет больше жидкости, по сравнению с другим за контрольный временной интервал. Аналогичным образом действует электрическое сопротивление. При увеличении номинала пассивного элемента создаются дополнительные препятствия прохождению тока.
Для расчета сложных схем используют технологию эквивалентных сопротивлений. Этим термином обозначают расчетную величину (Rэкв), которая равна сумме измеряемых параметров отдельных компонентов на определенном участке цепи. Проще всего сделать вычисления, если соединить резисторы (номиналы из примера) последовательно:
Rэкв = R1 + R2 = 50 + 150 = 200 Ом.
Ниже подробно рассмотрен вариант с параллельной схемой:
- по закону Ома для всей цепи действительно выражение: Iобщ = Uип/ Rэкв;
- в отдельных ветках: I1 = U1/ R1 (I2 = U2/ R2);
- по закону Кирхгофа для каждого провода: I = I1+ I2;
- преобразование перечисленных соотношений позволяет сделать промежуточный вывод: Uип/ Rэкв = U1/ R1 + U2/ R2;
- с учетом равенства напряжений: Uип = U1 = U2, можно переделать предыдущую формулу следующим образом: Uип/ Rэкв = Uип / R1 + Uип / R2 = Uип (1/R1 + 1/R2);
- делением на общий множитель Uип получают итоговое выражение: 1/Rэкв = 1/R1 + 1/R2.
Последняя позиция позволяет сделать несколько важных заключений:
- общая проводимость (величина, обратная электрическому сопротивлению) равна сумме проводимостей параллельных участков цепи;
- эквивалентное сопротивление можно вычислить делением единицы на проводимость;
- Rэкв при параллельном соединении всегда меньше самого меньшего из пассивных компонентов цепи.
Для переменного тока
В цепи переменного тока закон Ома может иметь некоторые особенности, описанные ниже.
Импеданс, Z
В цепи переменного тока, сопротивление кроме активной (R), может иметь как емкостную (C), так и индуктивную (L) составляющие. В этом случае вводится понятие электрического импеданса, Z (полного или комплексного сопротивления для синусоидального сигнала). Упрощенные схемы комплексного сопротивления приведены на рисунках ниже, слева для последовательного, справа для параллельного соединения индуктивной и емкостной составляющих.
Последовательное включение R, L, C
Параллельное включение R, L, C
Также, полное сопротивление, Z зависит не только от емкостной (C), индуктивной (L) и активной (R) составляющих, но и от частоты переменного тока.
| Импеданс, Полное сопротивление, Z | |
| При последовательном включении R, L, C | При параллельном включении R, L, C |
| Z=√(R2+(ωL-1/ωC)2) | Z=1/ √(1/R2+(1/ωL-ωC)2) |
| где, | |
| ω = 2πγ — циклическая, угловая частота; γ — частота переменного тока. |
Коэффициент мощности, Cos(φ)
Коэффициент мощности, в самом простом понимании, это отношение активной мощности (P) потребителя электрической энергии к полной (S) потребляемой мощности, т. е.
Cos(φ) = P / S
Он также показывает насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.Изменяется от 0 до 1. Если нагрузка не содержит реактивных составляющих (емкостной и индуктивной), то коэффициент мощности равен единице.Чем ближе Cos(φ) к единице, тем меньше потерь энергии в электрической цепи.
Исходя из вышеперечисленных понятий импеданса Z и коэффициента мощности Cos(φ), характерных для переменного тока, выведем формулу закона Ома, коэффициента мощности и их производные для цепей переменного тока:
| I = U / Z | где | I — сила переменного тока, измеряемая в Амперах, (A) |
| U — напряжение переменного тока, измеряемое в Вольтах, (V) | ||
| Z — полное сопротивление (импеданс), измеряется в Омах, (Ω) |
Производные формулы:
| Сила тока, | I= | U/Z | P/(U×Cos(φ)) | √(P/Z) |
| Напряжение, | U= | I×Z | P/(I×Cos(φ)) | √(P×Z) |
| Полное сопротивление, импеданс | Z= | U/I | P/I² | U²/P |
| Мощность, | P= | I²×Z | I×U×Cos(φ) | U²/Z |
Программа «КИП и А» имеет в своем составе блок расчета закона Ома как для постоянного и переменного тока, так и для расчета импеданса и коэффициента мощности Cos(φ). Скриншоты представлены на рисунках внизу:
Закон Ома для постоянного тока
Закон Ома для переменного тока
Расчет полного сопротивления
Расчет коэффициента мощности Cos(φ)
Калькулятор делителя напряжения
Разделитель напряжения представляет собой схему, используемую для создания напряжения, которое меньше или равно входному напряжению.
Выходное напряжение (V out )
Вольт (V)
Как найти выходное напряжение цепи делителя
Два делителя напряжения резистора являются одной из наиболее распространенных и полезных схем, используемых инженерами. Основная цель этой схемы заключается в уменьшении входного напряжения до более низкого значения в зависимости от отношения двух резисторов. Этот калькулятор помогает определить выходное напряжение схемы делителя с учетом входного (или источника) напряжения и значений резисторов
Обратите внимание на то, что выходное напряжение в реальных схемах может быть различным, поскольку резистор и сопротивление нагрузки (при подключении выходного напряжения) становятся факторами
Уравнение
$$ V_ {out} = V_ {in} * \ frac {R_ {2}} {R_ {1} + R_ {2}} $$
Где:
$$ V_ {out} $$ = Выходное напряжение. Это уменьшенное напряжение.
$$ V_ {in} $$ = Входное напряжение.
$$ R_ {1} $$ и $$ R_ {2} $$ = значения резистора. Отношение $$ \ frac {R_ {2}} {R_ {1} + R_ {2}} $$ определяет масштабный коэффициент.
Приложения
Поскольку делители напряжения довольно распространены, их можно найти в ряде приложений. Ниже приведены лишь некоторые из мест, где эта схема найдена.
потенциометры
Возможно, наиболее распространенной схемой делителя напряжения является то, что используется потенциометр, который является переменным резистором. Схематическое изображение потенциометра показано ниже:
«Горшок» обычно имеет три внешних контакта: два являются концами резистора, а один подключен к рычагу стеклоочистителя. Стеклоочиститель разрезает резистор пополам и перемещает его, регулируя соотношение между верхней половиной и нижней половиной резистора. Соедините два внешних выводы к напряжению (вход) и ссылку (земля) со средним (стеклоочистители штифтом) в качестве выходного контакта и вы сам делитель напряжения.
Уровневые сдвиги
Другая область, в которой используются делители напряжения, — это когда напряжение должно быть выровнено. Наиболее распространенным сценарием является взаимодействие сигналов между датчиком и микроконтроллером с двумя разными уровнями напряжения. Большинство микроконтроллеров работают при напряжении 5 В, в то время как некоторые датчики могут принимать только максимальное напряжение 3, 3 В. Естественно, вы хотите выровнять напряжение от микроконтроллера, чтобы избежать повреждения датчика. Пример схемы показан ниже:
Схема выше показывает схему делителя напряжения, включающую резистор 2 кОм и 1 кОм. Если напряжение от микроконтроллера составляет 5 В, то пониженное напряжение на датчик рассчитывается как:
$$ V_ {out} = 5 * \ frac {2k \ Omega} {2k \ Omega + 1k \ Omega} = 3.33 V $$
Этот уровень напряжения теперь безопасен для работы датчика
Обратите внимание, что эта схема работает только для выравнивания напряжений и не выравнивания
Ниже приведены некоторые другие комбинации резисторов, используемые для выравнивания часто встречающихся напряжений:
| Комбинация резисторов | использование |
| 4, 7 кОм и 6, 8 кОм | От 12 В до 5 В |
| 4, 7 кОм и 3, 9 кОм | 9V до 5V |
| 3, 6 кОм и 9, 1 кОм | От 12 В до 3, 3 В |
| 3, 3 кОм и 5, 7 кОм | От 9 В до 3, 3 В |
Чтение резистивного датчика
Многие датчики являются резистивными устройствами и большинством микроконтроллеров считывают напряжение, а не сопротивление. Таким образом, резистивный датчик обычно подключается в цепи делителя напряжения с резистором для взаимодействия с микроконтроллером. Пример установки показан ниже:
Термистор — это датчик, сопротивление которого изменяется пропорционально температуре. Скажем, что термистор имеет сопротивление комнатной температуре 350 Ом. Сопряженное сопротивление выбирается равным 350 Ом.
Когда термистор находится при комнатной температуре, выходное напряжение:
$$ V_ {out} = 5 * \ frac {350 \ Omega} {350 \ Omega + 350 \ Omega} = 2.5V $$
Когда температура увеличивается, сопротивление термистора изменяется до 350, 03 Ом, выход изменяется на:
$$ V_ {out} = 5 * \ frac {350.03 \ Omega} {350 \ Omega + 350.03 \ Omega} = 2.636V $$
Такое небольшое изменение напряжения обнаруживается микроконтроллером. Если функция передачи термистора известна, теперь можно рассчитать эквивалентную температуру.
Дальнейшее чтение
Техническая статья — Разделители напряжения и тока: что это такое и что они делают
Учебник — Глава 6 — Цепи Divider и законы Кирхгофа
Учебник — Потенциометр в качестве делителя напряжения
Рабочий лист — Цепь делителя напряжения
ЭДС. Закон Ома для полной цепи
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи, то есть в проводниках, подсоединённых к клеммам источника тока.
Как мы знаем, положительный заряд :
• уходит во внешнюю цепь с положительной клеммы источника;
• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;
• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.
https://youtube.com/watch?v=5DpeGSiPwOg
Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной.
Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила , направленная против движения заряда (т.е.
против направления тока).
Сторонняя сила
Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).
Рис. 1. Сторонняя сила
Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила не имеет отношения к стационарному электрическому полю — у неё, как говорят, неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.
Обозначим через работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы называется также работой источника тока.
Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, — это также работа сторонней силы по перемещению заряда по всей цепи.
Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.
Опыт показывает, что работа прямо пропорциональна перемещаемому заряду . Поэтому отношение уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается :
(1)
Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.
Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.
Ключевые показатели эффективности (KPI)
Ключевые показатели эффективности резисторов для каждого материала можно найти ниже:
| Характеристика | Металлопленочные резисторы | Толстопленочные резисторы | Тонкопленочные резисторы | Углеродные композиционные резисторы | Углеродные пленочные резисторы |
|---|---|---|---|---|---|
| Диапазон рабочих температур, °C | -55 … +125 | -55 … +130 | -55 … +155 | -40 … +105 | -55 … +155 |
| Максимальный температурный коэффициент сопротивления | 100 | 100 | 15 | 1200 | 250–1000 |
| Максимальное напряжение, В | 250–350 | 250 | 200 | 350–500 | 350–500 |
| Шум, мкВ на 1 В приложенного постоянного напряжения | 0,5 | 0,1 | 0,1 | 4 | 5 |
| Сопротивление изоляции, кОм | 10 | 10 | 10 | 10 | 10 |
| Изменение сопротивления при пайке, % | 0,20 | 0,15 | 0,02 | 2 | 0,50 |
| Изменение сопротивления при воздействии высокой температуры и влажности, % | 0,50 | 1 | 0,50 | 15 | 3,5 |
| Изменение сопротивления при длительном хранении, % | 0,10 | 0,10 | 0,00 | 5 | 2 |
| Изменение сопротивления при работе в течение 2000 часов при температуре 70°C, % | 1 | 1 | 0,03 | 10 | 4 |
Закон Ома для цепи
Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит. Возьмем замкнутую электрическую цепь и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).
Итак, закон Ома для рассматриваемого участка цепи имеет вид:
φ1-φ2=I*R, где
- I – ток, протекающий по участку цепи.
- R – сопротивление этого участка.
- φ1-φ2 – разность потенциалов между точками 1-2.
Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R. Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).
В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:
- U1=I*R1
- U2=I*R2
- Un=I*Rn
- U=I*(R1+R2+…+Rn
Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:
U=U1+U2+…+Un или U1/U2/…/Un=R1/R2/…/Rn
Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.
Закон Ома для участка цепи.
Для ЭДС
Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.
Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.
Для полной цепи
Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.
Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.
Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:
I = U / (R + r)
Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.
Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.
https://youtube.com/watch?v=f2rpF5ztAr0
Разновидности
Бывает двух видов: постоянным и переменным. Первое есть в электростатических видах цепей и тех, которые имеют постоянный ток. Переменный встречается там, где есть синусоидальная энергия
Важно, что синусоидальная энергия делится на действующее, мгновенное со средневыпрямленным. Единица измерения напряжения электрического тока вольт
Стоит также отметить, что величина энергии между фазами называется линейной фазой, а показатель тока земли и фаз — фазным. Подобное правило используется во всех воздушных линиях. На территории Российской Федерации в электрической бытовой сети стандартное — 380 вольт, а фазное — 220 вольт.
Основные разновидности
Постоянное напряжение
Постоянным называется разность между электрическими потенциалами, при которой остается такой же величина с перепадами полярности на протяжении конкретного периода. Главным преимуществом постоянной энергии является тот факт, что отсутствует реактивная мощность. Это означает, что вся мощность, которая вырабатывается при помощи генератора, потребляется нагрузкой за исключением проводных потерь. Течет по всему проводниковому сечению.
Что касается недостатков, есть сложность повышения со снижением энергии, то есть в моменте преобразования ее из-за конструкции преобразователей и отсутствия мощных полупроводниковых ключей. К тому же сложно развязывается высокая и низкая энергия.
Обратите внимание! Используется постоянная энергия в электронных схемах, гальванических элементах, аккумуляторах, электролизных установках, сварочных инструментах, инверторных преобразователях и многих других приборах. Вам это будет интересно Установка двухзонного счетчика
Вам это будет интересно Установка двухзонного счетчика
Постоянный ток
Переменное напряжение
Переменным называется ток, изменяющийся по величине и направлению периодически, но при этом сохраняющий свое направление в электроцепи неизменно. Нередко его называют синусоидальным. Одно направление, в котором движется энергия, называется положительным, а другое — отрицательным. Поэтому получающаяся величина называется положительной и отрицательной. Такой показатель является алгебраической величиной. В ответ на вопрос, как называется единица измерения напряжения, необходимо отметить, что это вольт. Значение его определяется по направлению. Максимальное значение — амплитуда. Бывает он:
двухфазным;
Двухфазный
трехфазным;
Трехфазный
многофазным.
Многофазный Используется активно в промышленности, на электрической станции, на трансформаторной подстанции и передается в каждый дом при помощи линий электрических передач. Больше всего используется три фазы для подключения. Подобная электрификация распространена на многих железных дорогах.
Обратите внимание! Стоит отметить, что имеются также некоторые виды двухсистемных электровозов, которые работают во многих случаях на переменном показателе. Переменный ток
Переменный ток
Расчет резистора для светодиода — порядок, формулы, особенности подключения
Светодиод — прибор, который при прохождении через него тока излучает свет.
В зависимости от типа используемого материала для изготовления прибора, светодиоды могут излучать свет различного цвета. Эти миниатюрные, надежные, экономичные приборы используются в технике, для освещения и в рекламных целях.
Особенности включения светодиода
Светодиод обладает такой же вольтамперной характеристикой, как и обычный полупроводниковый диод. При этом при повышении прямого напряжения на светодиоде проходящий через него ток резко возрастает.
Например, для зеленого светодиода типа WP710A10LGD компании Kingbright при изменении приложенного прямого напряжения от 1,9 В до 2 В ток меняется в 5 раз и достигает 10 мА. Поэтому при прямом подключении светодиода к источнику напряжения при небольшом изменении напряжения ток светодиода может возрасти до очень большого значения, что приведет к сгоранию p-n перехода и светодиода.
Другой метод маркировки — цветная — предназначен для обозначения параметров резисторов посредством цветных полосок и кольц.
Такого явления не произойдет, если светодиод питается от специального источника стабилизированного тока – драйвера.
При использовании драйвера с постоянным стабилизированным током обеспечиваются лучшие характеристики излучения светодиода, и, кроме того, увеличивается срок его работы. Однако такие источники тока дорогие и используются только для ответственных случаев.
При отсутствии источника со стабилизированным током для предотвращения сгорания светодиода от нестабильности питающего напряжения последовательно с ним обычно включается ограничивающий резистор.
Формулы расчета резистора для светодиода
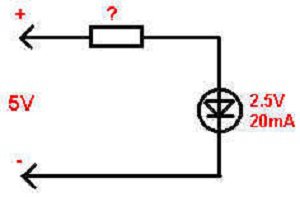В общем случае расчет сопротивления резистора для светодиодов производится по закону Ома. Зная напряжение и ток, можно определить величину сопротивления участка цепи:
R=U/I, где:
- R- сопротивление, Ом;
- U- напряжение на участке цепи, В;
- I-ток, протекающий в цепи, А.
В данном случае, выбрав необходимое рабочее значение тока светодиода Iсв и определив по вольтамперной характеристике рабочее напряжение светодиода Uсв, с учетом напряжения питания схемы Uпит можно определить величину сопротивления ограничивающего резистора Rогр:
Rогр=(Uпит-Uсв)/(Iсв*0,75)
Коэффициент 0,75 предназначен для обеспечения некоторого запаса.
Определив величину сопротивления, надо найти ближайший к нему номинал резистора.
Pрас =Iсв²*Rогр, где:
- Pрас — мощность, рассеиваемая на ограничивающем резисторе, Вт;
- Iсв — ток светодиода, А;
- Rогр – сопротивление ограничивающего резистора, Ом.
После расчета мощности резистора для светодиода необходимо выбрать элемент со стандартным максимально допустимым значением. При этом необходимо ориентироваться на большую из ближайших к рассчитанной мощности величин.
Параллельное и последовательное включение светодиодов
При параллельном включении светодиодов необходимо иметь в виду, что соединение к одному ограничивающему резистору не рекомендуется. Это связано с тем, что даже светодиоды одного типа имеют большие разбросы по току.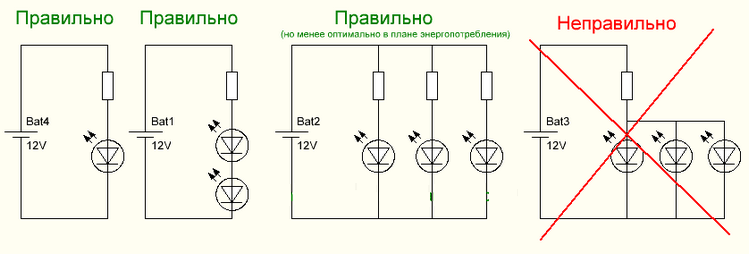
Это приводит к тому, что при таком включении через светодиоды будут течь токи разной величины. Светодиоды будут светиться с разной яркостью. Кроме того, в случае, если сгорит один источник света, то по остальным светодиодам потечет большой ток, что может привести к выходу из строя всех остальных.
Детальнее ознакомиться с принципом работы устройства защитного отключения можно тут, а о схемах подключения — здесь.
Поэтому при параллельном включении светодиодов обычно к каждому прибору последовательно подключают свой ограничивающий резистор. Расчет сопротивления и мощности такого резистора ничем не отличается от ранее рассмотренного случая.
При последовательном включении светодиодов необходимо включать приборы одного типа.
Кроме того, надо учитывать то, что напряжение источника должно быть не меньше суммарного рабочего напряжения всей группы светодиодов.
Выводы:
- Светодиоды — широко распространенные приборы, используемые в технике, для освещения и рекламы.
- Во избежание выхода из строя светодиодов из-за их чувствительности к изменениям напряжения для них часто используют ограничивающие резисторы.
- Расчет значения сопротивления ограничивающего резистора делается на основе закона Ома.
Входное и выходное сопротивление
Все электронные устройства состоят из блоков. Их еще часто называют каскады, модули, узлы и т.д. Например, (рис. 1) состоит из двух блоков.
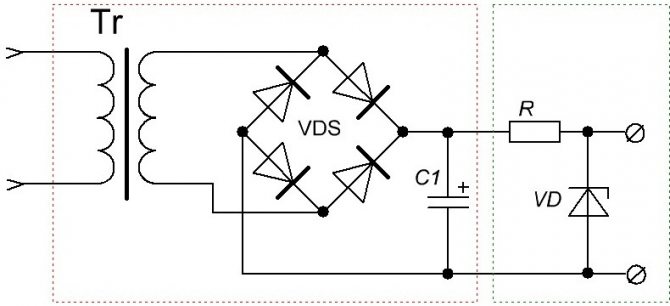
Рис. 1 — Схема источника питания
На рисунке 1 в левом блоке мы получаем постоянное напряжение, а в правом блоке его стабилизируем (рис. 2).
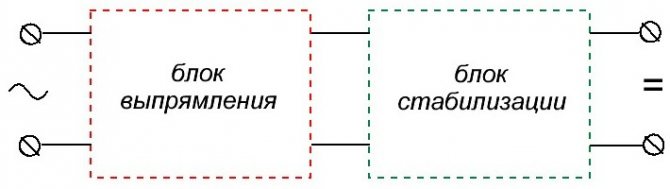
Рис. 2 — Блочная схема источника питания
Блочная схема — это условное деление. В этом примере мы могли бы даже взять трансформатор, как отдельный блок, который понижает переменное напряжение одного номинала к другому. Как нам удобнее, так и делим на блоки нашу электронную безделушку. Метод «от простого к сложному» полностью работает в нашем мире. На низшем уровне находятся радиоэлементы, на высшем — готовое устройство, например, телевизор.
Как вы поняли, любое устройство состоит из блоков, которые выполняют определенную функцию.
На словах все выходит прекрасно, но всегда есть подводные камни, которые следует изучить, чтобы начать проектировать электронные устройства. Некоторые из этих камушков называются входным и выходным сопротивлением.
Резистор хоть и обладает сопротивлением, но это активное сопротивление. Катушка индуктивности и конденсатор будут уже обладать, так называемым, реактивным сопротивлением.
Если прислушаться фразам, то входное сопротивление — это сопротивление какого-то входа, а выходное — сопротивление какого-либо выхода. Ну да, все почти так и есть. И где же нам найти в схеме эти входные и выходные сопротивления? А вот «прячутся» они в самих блоках радиоэлектронных устройств.
Способы снижения потерь в кабеле
Кроме нарушения нормальной работы электроприборов, падение напряжения в проводах приводит к дополнительным расходам на электроэнергию. Уменьшить эти затраты можно разными способами:
- Увеличение сечения питающих проводов. Этот метод требует значительных расходов на замену кабелей и тщательной проверки экономической целесообразности;
- Уменьшение длины линии. Прямая, соединяющая две точки, всегда короче кривой или ломаной линии. Поэтому при проектировании сетей электроснабжения линии следует прокладывать максимально коротким прямым путём;
- Снижение окружающей температуры. При нагреве сопротивление металлов растёт, и увеличиваются потери электроэнергии в кабеле;
- Уменьшение нагрузки. Этот вариант возможен при наличии большого числа потребителей и источников питания;
- Приведение cosφ к 1 возле нагрузки. Это уменьшает потребляемый ток и потери.
К сведению. Улучшение вентиляции в кабельных лотках и других конструкциях приводит к снижению температуры, сопротивления и потерь в линии.
Для достижения максимального эффекта необходимо комбинировать эти способы между собой и с другими методами энергосбережения.
Расчёт падения напряжения и потерь электроэнергии в кабеле важен при проектировании систем электроснабжения и кабельных линий.
