Фактор мощности в цепях переменного тока, влияние на потребителей

Как измерить коэффициент мощности

Если вы не знаете точный коэфф. мощности своего прибора, или его нет на бирке, можно ли измерить косинус фи в домашних условиях, не прибегая к различным формулам и вычислениям? Конечно можно.

Для этого достаточно приобрести широко распространенный инструмент — цифровой ваттметр в розетку.

Подключая любое оборудование через него, можно легко без замеров и сложных вычислений, узнать фактический cos ϕ.

Зачастую, фактические данные могут быть даже точнее, чем написанные на шильдике, которые рассчитаны для идеальных условий.

Если он слишком низкий, что делать, чтобы привести его значение как можно ближе к единице? Можно это дело определенным образом компенсировать. Например, с помощью конденсаторов.

Однако это тема совсем другой статьи.

https://youtube.com/watch?v=-MBd7x6GmHU

Что такое коэффициент мощности?

Чтобы лучше уяснить, что такое коэффициент мощности, нужно начать с нескольких основных понятий:

Активная мощность (кВт), также называемая полезной мощностью или действующей мощностью. Это мощность, которая реально приводит в действие оборудование и выполняет полезную работу.

Реактивная мощность (квар). Это мощность, необходимая устройствам, принцип действия которых основан на использовании электромагнитного поля (трансформаторов, электродвигателей, реле) для вырабатывания магнитного потока.

Полная мощность (кВА). Это векторная сумма активной и реактивной мощностей.

Рассмотрим простую аналогию, чтобы лучше уяснить эти понятия.

Допустим, вы находитесь на стадионе в жаркий день и заказываете кружку своего любимого пива. Та часть вашей порции, которая утоляет жажду, представляет активную мощность (рис. 1).

Увы, жизнь несовершенна. Вместе с этим вы получаете и пену. И давайте посмотрим правде в глаза – пена нисколько не утоляет жажду. Эта пена представляет реактивную мощность. Общее содержимое кружки является суммой активной мощности (пива), кВт, и реактивной мощности (пены), квар.

Теперь, после того как мы разобрались с основными понятиями, можно перейти к коэффициенту мощности.

Коэффициент мощности (КМ) – это отношение активной мощности к полной мощности:

КМ = кВт/(кВт + квар)

Если вернуться к нашей аналогии с кружкой пива, коэффициент мощности представляет собой отношение количества пива (кВт) к общему содержимому кружки, то есть к количеству пива с пеной (кВА).

КМ = кВт/(кВт + квар) = пиво/(пиво + пена)

Таким образом, при данной полной мощности:

· чем больше пены (чем выше процент реактивной мощности), тем меньше отношение активной мощности (пиво) к полной мощности (пиво с пеной) и тем меньше коэффициент мощности;

· чем меньше пены (чем ниже процент реактивной мощности), тем выше отношение активной мощности (пиво) к полной мощности (пиво с пеной). Если пена (реактивная мощность) приближается к нулю, коэффициент мощности приближается к единице.

Наша аналогия с пивной кружкой немного упрощена. В реальности необходимо определять векторную сумму реактивной и активной мощностей. Поэтому следующим шагом будет рассмотрение угла между этими векторами.

Рассмотрим другую аналогию.

Человек тянет тяжёлый груз (рис. 2). Мощность, которую он прикладывает в прямом направлении, то есть в том направлении, куда он хочет доставить груз, — это активная мощность (кВт).

К сожалению, человек не может тянуть груз строго горизонтально (он получит сильные боли в спине), поэтому высота его плеч добавляет некоторое количество реактивной мощности (квар).

Полная мощность, прикладываемая человеком (кВА), – это векторная сумма реактивной и активной мощностей.

Соотношение между активной, реактивной и полной мощностями, а также определение коэффициента мощности иллюстрируются треугольником мощностей, изображённым на рис. 3.

КМ = кВт/кВА = cosθ

квар/кВА = sinθ

кВА = кВт2 + квар2 = V х I х.

Заметим, что в мире нашей мечты по аналогии с кружкой пива:

реактивная мощность должна быть очень мала (количество пены стремится к нулю);
активная мощность и полная мощность должны быть почти равны друг другу

(больше пива, меньше пены).

Аналогично в идеальном мире по аналогии с человеком, который тащит груз:

реактивная мощность очень мала (стремится к нулю);
активная мощность и полная мощность почти равны друг другу (человеку не нужно
тратить энергию на усилие, направленное вдоль его тела);
угол θ между векторами активной и полной мощности стремится к нулю;
cosθ стремится к единице;
коэффициент мощности стремится к единице.

Поэтому чтобы иметь эффективную систему (будь то кружка пива или человек, который тащит тяжёлый груз), мы должны иметь коэффициент мощности, как можно более близкий к 1,0.

Однако бывает, что система распределения электроэнергии имеет коэффициент мощности гораздо меньше 1,0. Далее мы увидим, к чему это приводит.

Добавляем знаки и специальные символы в Microsoft Word

Вероятнее всего, вы хотя бы раз сталкивались с необходимостью вставить в MS Word знак или символ, которого нет на компьютерной клавиатуре. Это могло быть, к примеру, длинное тире, символ градуса или правильной дроби, а также много чего другого. И если в некоторых случаях (тире и дроби) на помощь приходит функция автозамены, то в других все оказывается намного сложнее.

Мы уже писали о вставке некоторых специальных символов и знаков, в этой статье мы расскажем о том, как быстро и удобно добавлять в документ MS Word любые из них.

Вставка символа

1. Кликните в том месте документа, куда необходимо вставить символ.

2. Перейдите во вкладку “Вставка” и нажмите там кнопку “Символ”, которая находится в группе “Символы”.

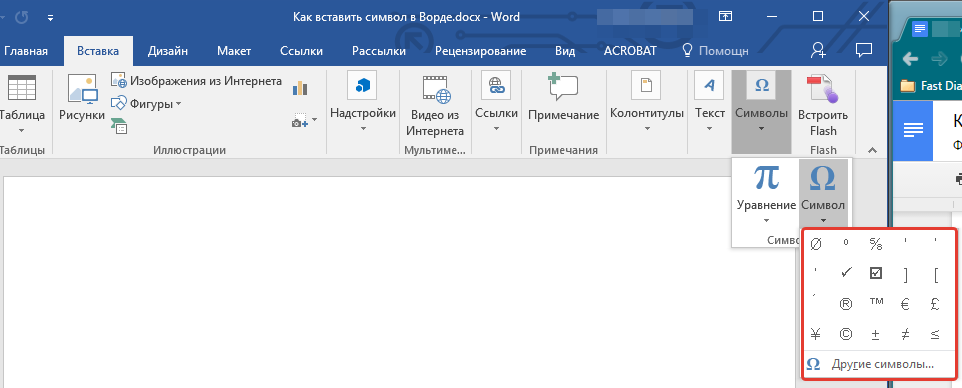
3. Выполните необходимое действие:

Выберите в развернувшемся меню нужный символ, если он там есть.

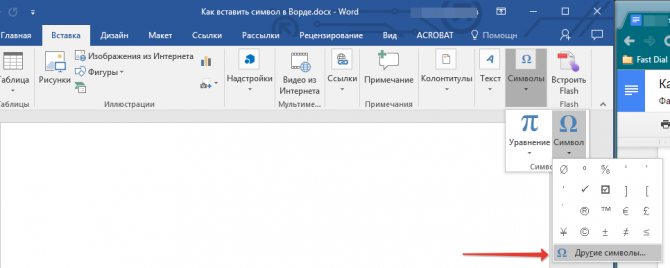
Если же нужный символ в этом небольшом окошке будет отсутствовать, выберите пункт “Другие символы” и найдите его там. Кликните по необходимому символу, нажмите кнопку “Вставить” и закройте диалоговое окно.

Примечание: В диалоговом окне “Символ” содержится очень много различных символов, которые сгруппированы по тематикам и стилям. Для того, чтобы быстрее найти нужный символ, вы можете в разделе “Набор” выбрать характерный для этого символа, например, “Математические операторы” для того, чтобы найти и вставить математические символы. Также, можно изменять шрифты в соответствующем разделе, ведь во многих из них тоже есть различные символы, отличные от стандартного набора.

4. Символ будет добавлен в документ.

Вставка специального знака

1. Кликните в том месте документа, куда необходимо добавить специальный знак.

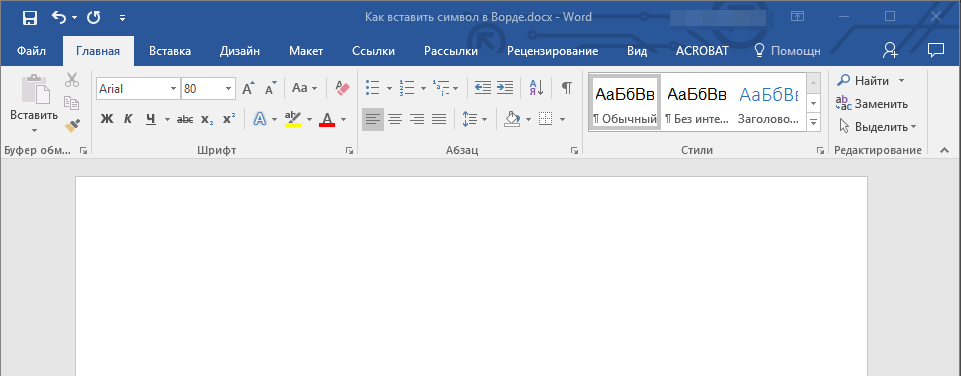
2. Во вкладке “Вставка” откройте меню кнопки “Символы” и выберите пункт “Другие символы”.

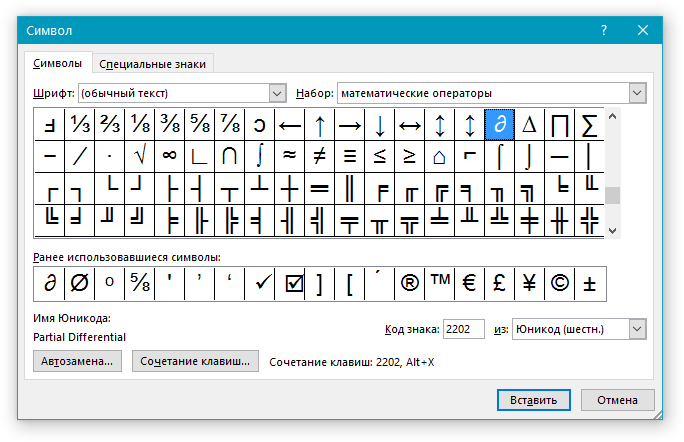
3. Перейдите во вкладку “Специальные знаки”.

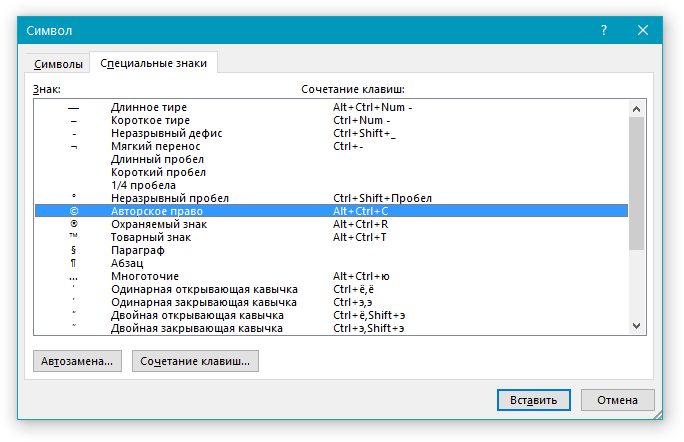
4. Выберите необходимый знак, кликнув по нему. Нажмите кнопку “Вставить”, а затем “Закрыть”.

5. Специальный знак будет добавлен в документ.

Примечание: Обратите внимание, что в разделе “Специальные знаки” окна “Символ”, помимо самих специальных знаков вы также можете увидеть горячие комбинации клавиш, которые можно использовать для их добавления, а также настроить автозамену для конкретного символа

Как найти активную, реактивную и полную мощность

Активная мощность относится к энергии, которая необратимо расходуется источником за единицу времени для выполнения потребителем какой-либо полезной работы. В процессе потребления, как уже было отмечено, она преобразуется в другие виды энергии.

В цепи переменного тока значение активной мощности определяется, как средний показатель мгновенной мощности за установленный период времени. Следовательно, среднее значение за этот период будет зависеть от угла сдвига фаз между током и напряжением и не будет равной нулю, при условии присутствия на данном участке цепи активного сопротивления. Последний фактор и определяет название активной мощности. Именно через активное сопротивление электроэнергия необратимо преобразуется в другие виды энергии.

При выполнении расчетов электрических цепей широко используется понятие реактивной мощности. С ее участием происходят такие процессы, как обмен энергией между источниками и реактивными элементами цепи. Данный параметр численно будет равен амплитуде, которой обладает переменная составляющая мгновенной мощности цепи.

Существует определенная зависимость реактивной мощности от знака угла ф, отображенного на рисунке. В связи с этим, она будет иметь положительное или отрицательное значение. В отличие от активной мощности, измеряемой в ваттах, реактивная мощность измеряется в вар – вольт-амперах реактивных. Итоговое значение реактивной мощности в разветвленных электрических цепях представляет собой алгебраическую сумму таких же мощностей у каждого элемента цепи с учетом их индивидуальных характеристик.

Основной составляющей полной мощности является максимально возможная активная мощность при заранее известных токе и напряжении. При этом, cosф равен 1, когда отсутствует сдвиг фаз между током и напряжением. В состав полной мощности входит и реактивная составляющая, что хорошо видно из формулы, представленной выше. Единицей измерения данного параметра служит вольт-ампер (ВА).

Пусть приемник электроэнергии присоединен к источнику синусоидального напряжения u(t) = Usin(ωt) и потребляет синусоидальный ток i(t) = I sin (ωt -φ), сдвинутый по фазе относительно напряжения на угол φ. U и I – действующие значения. Значение мгновенной мощности на зажимах приемника определяется выражением

p(t) = u(t) ?i(t) = 2UI sin(ωt) sin (ωt -φ) = UI cos φ — UI cos (2ωt -φ)

(5.1)

и является суммой двух величин, одна из которых постоянна во времени, а другая пульсирует с двойной частотой.

Среднее значение p(t) за период Т называется активной мощностью и полностью определяется первым слагаемым уравнения (5.1):

Активная мощность характеризует энергию, расходуемую необратимо источником в единицу времени на производство полезной работы потребителем. Активная энергия, потребляемая электроприёмниками, преобразуется в другие виды энергии: механическую, тепловую, энергию сжатого воздуха и газа и т. п.

Скорость роста

По словам Харди и Райта, порядок φ ( n ) «всегда почти n ».

Первый

LimКак делаφ(п)пзнак равно1,{\ displaystyle \ lim \ sup {\ frac {\ varphi (n)} {n}} = 1,}

но когда n стремится к бесконечности, для всех δ > 0

φ(п)п1-δ→∞.{\ displaystyle {\ frac {\ varphi (n)} {n ^ {1- \ delta}}} \ rightarrow \ infty.}

Эти две формулы можно доказать, используя немногим больше, чем формулы для φ ( n ) и функции суммы делителей σ ( n ) .

Фактически при доказательстве второй формулы неравенство

6π2<φ(п)σ(п)п2<1,{\ displaystyle {\ frac {6} {\ pi ^ {2}}} <{\ frac {\ varphi (n) \ sigma (n)} {n ^ {2}}} <1,}

верно для n > 1 , доказано.

У нас также есть

Limинфφ(п)пбревно⁡бревно⁡пзнак равное-γ.{\ displaystyle \ lim \ inf {\ frac {\ varphi (n)} {n}} \ log \ log n = e ^ {- \ gamma}.}

Здесь γ является постоянная Эйлера , γ = 0,577215665 … , поэтому е γ = 1.7810724 … и е — γ = 0.56145948 … .

Доказательство этого не совсем требует теоремы о простых числах . Поскольку log log n стремится к бесконечности, эта формула показывает, что

Limинфφ(п)пзнак равно{\ displaystyle \ lim \ inf {\ frac {\ varphi (n)} {n}} = 0.}

На самом деле, правда больше.

φ(п)>пеγбревно⁡бревно⁡п+3бревно⁡бревно⁡пдля п>2{\ displaystyle \ varphi (n)> {\ frac {n} {e ^ {\ gamma} \; \ log \ log n + {\ frac {3} {\ log \ log n}}}} \ quad {\ text {for}} n> 2}

а также

φ(п)<пеγбревно⁡бревно⁡пбесконечно много п.{\ displaystyle \ varphi (n) <{\ frac {n} {e ^ {\ gamma} \ log \ log n}} \ quad {\ text {для бесконечного числа}} n.}

Второе неравенство показал Жан-Луи Николя . Рибенбойм говорит: «Метод доказательства интересен тем, что неравенство показано, во-первых, в предположении, что гипотеза Римана верна, а во-вторых, в противоположном предположении».

Для среднего заказа имеем

φ(1)+φ(2)+⋯+φ(п)знак равно3п2π2+О(п(бревно⁡п)23(бревно⁡бревно⁡п)43)в качестве п→∞,{\ displaystyle \ varphi (1) + \ varphi (2) + \ cdots + \ varphi (n) = {\ frac {3n ^ {2}} {\ pi ^ {2}}} + O \ left (n ( \ log n) ^ {\ frac {2} {3}} (\ log \ log n) ^ {\ frac {4} {3}} \ right) \ quad {\ text {as}} n \ rightarrow \ infty ,}

благодаря Арнольду Вальфизу , в его доказательстве используются оценки экспоненциальных сумм, полученные И. М. Виноградовым и Н. М. Коробовым (в настоящее время это наиболее известная оценка такого типа). «Большой O » обозначает количество, которое ограничено константой , кратной функции п внутри круглых скобок (которая мала по сравнению с п 2 ).

Этот результат может быть использован для доказательства того, что вероятность того, что два случайно выбранных числа будут относительно простыми, равна 6π 2.

Коэффициент мощности

Коэффициент использования производственной мощности

Косинус фи является тем параметром, который характеризует деформацию синусоиды тока, используемого от электрической сети переменного тока, согласно картинке ниже. Он является основным критерием, определяющим потери в проводах и на внутреннем сопротивлении сети.

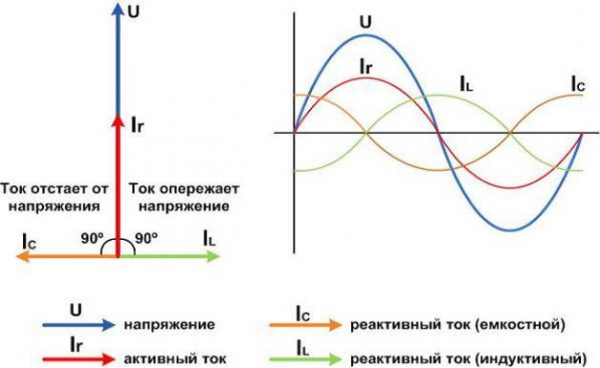
Искажение тока

Косинус фи, основываясь на таблице стандартов энергопотребления, имеет такие показатели:

Отличный – при значениях от 0,95 до 1;
Хороший – при значениях от 0,8 до 0,95;
Удовлетворительный – при значениях от 0,65 до 0,8;
Неудовлетворительный – при значениях ниже 0,65.

Коэффициент мощности асинхронного двигателя и генератора

Поскольку статор и ротор асинхронного двигателя выполнены путем намотки медного провода, то, помимо активной составляющей, имеется индуктивная и емкостная составляющая сопротивления. Соответственно, каждую половину периода колебания с частотой f в сеть возвращается некоторое количество электричества. Негативными последствиями такой операции, помимо паразитного нагрева проводов, является, по сути, вырабатывание генератором электроэнергии, часть которой расходуется впустую, путем циркулирования между генератором и двигателем. Для частных случаев величина реактивных токов является малой, однако если речь идет о больших предприятиях, то величина реактивной мощности может быть настолько велика, что может повлиять на энергосистему целого региона.

Наличие заниженного коэффициента мощности влечет за собой ряд неблагоприятных проявлений:

Применение в линиях электропередач проводов большего сечения и использование электрических и трансформаторных станций большей мощности;
Снижение коэффициента полезного действия генерирующих и трансформирующих элементов цепи;
Снижение полезного напряжения и мощности в проводах.

Мероприятия по увеличению cosφ направлены на:

Максимальное сокращение потерь электрической энергии;
Применение оптимального количества цветных металлов в процессе формирования электропроводящей аппаратуры;
Использование электрических двигателей, трансформаторов, генераторов и других устройств, работающих на переменном токе, с максимальной пользой и для увеличения их срока службы. Соответственно, улучшение коэффициента мощности неизбежно влечет за собой увеличение коэффициента полезного действия питающей сети.

К основным методам по увеличению коэффициента мощности относятся:

Компенсация реактивного компонента путем включения в цепь элемента с обратным действием. Промышленные предприятия, имеющие в питающей сети большой индуктивный компонент, с целью его уменьшения применяют электротехнику, собранную на конденсаторах. В связи с этим циркуляция паразитных составляющих проходит между потребителями и установкой, не принося вред питающей сети;
Осмысленный подход к технологическому процессу и разумное рассредоточение нагрузок с целью увеличения коэффициента мощности.

Для таких целей прибегают к таким мероприятиям:

Использование оптимальной нагрузки на электрические двигатели в процессе эксплуатации;
Исключить использование оборудования, потребляющего индуктивную мощность, без нагрузки или в режиме холостого хода;
Использование электрических двигателей с другими характеристиками.

Разобравшись, что такое коэффициент мощности, и осознав техпроцессы, проходящие в питающей сети, при наличии паразитных мощностей можно обоснованно подходить к вопросу выбора оборудования, отвечающего характеристикам этой сети. Второстепенный, на первый взгляд, показатель косинус фи является важным критерием, как для поставщиков электрической энергии, так и для различных ее потребителей.

Некоторые ценности

Первые 100 значений (последовательность A000010 в OEIS ) показаны в таблице и на графике ниже:

График первых 100 значений

φ ( n ) для 1 ≤ n ≤ 100
+	1	2	3	4	5	6	7	8	9	10
1	1	2	2	4	2	6	4	6	4
10	10	4	12	6	8	8	16	6	18	8
20	12	10	22	8	20	12	18	12	28 год	8
30	30	16	20	16	24	12	36	18	24	16
40	40	12	42	20	24	22	46	16	42	20
50	32	24	52	18	40	24	36	28 год	58	16
60	60	30	36	32	48	20	66	32	44 год	24
70	70	24	72	36	40	36	60	24	78	32
80	54	40	82	24	64	42	56	40	88	24
90	72	44 год	60	46	72	32	96	42	60	40

На графике справа верхняя линия y = n — 1 является верхней границей, действительной для всех n, кроме одного, и достигается тогда и только тогда, когда n — простое число. Простая нижняя граница есть , которая довольно нечеткая: на самом деле нижняя граница графика пропорциональнаφ(п)≥п2{\ displaystyle \ varphi (п) \ geq {\ sqrt {n / 2}}}пжурнал журнал n.

Что вызывает низкий коэффициент мощности cos φ (cos фи) в электрической системе?

В разделе Техника на вопрос для чего нужен тангенс фи в электроэнергетики? При tgф<0 потребитель выдает реактивную мощность (емкостной характер) , при tgф>1 потребитель потребляет реактивную мощность (индуктивный характер).

Рассмотрев треугольник сопротивлений, можно понять смысл термина «тангенс фи». Это отношение между реактивной и активной составляющими нагрузки. Тангенс угла потерь также используется в электроэнергетике, но более привычным является показатель cos(φ).

Часть электрической мощности, пришедшая к потребителю, используется для совершения полезной работы и тепловое рассеяние на нагрузке у потребителя. Почему фазовый сдвиг приводит к потерям электроэнергии? Если активное сопротивление проводника просто рассеивает электроэнергию, переводя ее в тепловую, то фазовый сдвиг между током и напряжением приводит к повышенному расходу энергии на электростанции. Отношение активной мощности, потребляемой в нагрузке, и полной мощности, подаваемой на нагрузку по линии электропередач, численно равно cos(φ), где φ – угол фазового сдвига между током и напряжением. С другой стороны, 0% — крайне нежелательный вариант, когда φ=π/2, cos(φ)=0, при этом вся подаваемая мощность переменного тока отражается от реактивной нагрузки и рассеивается в подводящих проводах.

Р — мощность активная,Q — мощность реактивная. Главный инженер ЭнергосбытаА.

Мне тут в акте о разграничении балансовой ответственности МКС прописал Базовый коэффициент реактивной мощности тангенс Фи, который равен 0,2. Это как понимать?

Активный и реактивный токи, протекающие в проводе, складываются в один общий ток, который замеряется амперметром. Отношение активной мощности к полной называется коэффициентом мощности. Для удобства технических расчетов коэффициент мощности выражают через косинус условного угла «фи» (cosφ).

Коэффициент мощности (cos φ) это параметр, характеризующий искажения формы тока, потребляемого от электросети переменного тока. Важный показатель потребителя электроэнергии. Для оценки и расчетов цепей переменного тока используются действующие значения тока и напряжения. Вольтметры и амперметры переменного тока показывают именно действующие значения. Полная мощность в цепях переменного тока равна квадратному корню из суммы квадратов активной и реактивной мощностей. Фазового сдвига нет, cos φ = 1, вся энергия из сети переходит в активную мощность на нагрузке.

Косинус фи (cos φ) — это косинус угла между фазой напряжения и фазой тока. При активной нагрузке фаза напряжения совпадает с фазой тока, φ (между фазами) равен 0 (нулю). Попытаемся вычислить мощность для простоты возьмем максимальное значение напряжения равное 1(100%) в этот момент ток равен 0(нулю) соответственно их произведение, то есть мощность равны 0(нулю). И наоборот когда ток максимальный напряжение равно нулю. Получается что полезная, активная мощность равна 0(нулю). Счетчики активной мощности фиксируют соответственно только активную мощность.

Попробуем популярно объяснить причину такого уважения электриков к тригонометрической функции cos φ. «Косинус-фи» в электроэнергетике еще называют коэффициентом мощности. Численно коэффициент мощности равен косинусу этого фазового сдвига. Источниками реактивной мощности в сети переменного тока являются катушки индуктивности и конденсаторы. Большинство потребителей электрической энергии имеют обмотки на магнитопроводах, т.е. представляют собой индуктивность. Тогда в однофазной цепи cos φ = P / (U х I), где Р, U, I — показания ваттметра, вольтметра и амперметра, соответственно.

В тренде:

Как Путин обошел Обаму в списке «Форбс»?Если это действительно так, то Путин с легкостью попадает в первую десятку богатейших людей мира по версии журнала Forbes. Этот журнал ежегодно проводит публикацию рейтинга самых богатых
Когда можно съесть банан, а когда нельзяЛучше всего их кушать утром, когда ваш организм так жаден к питательным веществам. Возможно, банан – именно то, чего в этот момент так не хватает организму. Съеденный банан перед сном
Типичные ошибки при приготовлении пломбираЕго разводят в молоке, а после заваривают до густоты. Если в пломбир добавляют ароматизаторы или ягоды и фрукты, то делать это нужно на заключительном этапе приготовления, уже пред тем как

Золотое сечение в природе, человеке, искусстве

Прежде, чем мы начнем, хотелось бы уточнить ряд неточностей. Во-первых, само определение золотого сечения в данном контексте не совсем верно. Дело в том, что само понятие «сечение» — это термин геометрический, обозначающий всегда плоскость, но никак не последовательность чисел Фибоначчи.

И, во-вторых, числовой ряд и соотношение одного к другому, конечно, превратили в некий трафарет, который можно накладывать на все, что кажется подозрительным, и очень радоваться, когда есть совпадения, но все же, здравый смысл терять не стоит.

Однако, «все смешалось в нашем королевстве» и одно стало синонимом другого. Так что в общем и целом, смысл от этого не потерялся. А теперь к делу.

Вы удивитесь, но золотое сечение, точнее пропорции максимально приближенные к нему, можно увидеть практически везде, даже в зеркале. Не верите? Давайте с этого и начнем.

Пропорции золотого сечения в человеке

Знаете, когда я училась рисовать, то нам объясняли, как проще строить лицо человека, его тело и прочее. Все надо рассчитывать, относительно чего-то другого.

Все, абсолютно все пропорционально: кости, наши пальцы, ладони, расстояния на лице, расстояние вытянутых рук по отношению к телу и так далее. Но даже это не все, внутреннее строение нашего организма, даже оно, приравнивается или почти приравнивается к золотой формуле сечения. Вот какие расстояния и пропорции:

от плеч до макушки к размеру головы = 1:1.618
от пупка до макушки к отрезку от плеч до макушки = 1:1.618
от пупка до коленок и от коленок до ступней = 1:1.618
от подбородка до крайней точки верхней губы и от нее до носа = 1:1.618

Разве это не удивительно!? Гармония в чистом виде, как внутри, так и снаружи. И именно поэтому, на каком-то подсознательном что-ли уровне, некоторые люди не кажутся нам красивыми, даже если у них крепкое подтянутое тело, бархатная кожа, красивые волосы, глаза и прочее и все остальное. Но, все равно, малейшее нарушений пропорций тела, и внешность уже слегка «режет глаза».

Короче говоря, чем красивее кажется нам человек, тем ближе его пропорции к идеальным. И это, кстати, не только к человеческому телу можно отнести.

Золотое сечение в природе и ее явлениях

Классическим примером золотого сечения в природе является раковина моллюска Nautilus pompilius и аммонита. Но это далеко не все, есть еще много примеров:

в завитках человеческого уха мы можем увидеть золотую спираль;
ее же (или приближенную к ней) в спиралях, по которым закручиваются галактики;
и в молекуле ДНК;
по ряду Фибоначчи устроен центр подсолнуха, растут шишки, середина цветов, ананас и многие другие плоды.

Друзья, примеров настолько много, что я просто оставлю тут видеоролик (он чуть ниже), чтобы не перегружать текстом статью. Потому что, если эту тему копать, то можно углубиться в такие дебри: еще древние греки доказывали, что Вселенная и, вообще, все пространство, — спланировано по принципу золотого сечения.

Вы удивитесь, но эти правила можно отыскать даже в звуке. Смотрите:

Наивысшая точка звука, вызывающая боль и дискомфорт в наших ушах, равна 130 децибелам.
Делим пропорцией 130 на число золотого сечения φ = 1,62 и получаем 80 децибел — звук человеческого крика.
Продолжаем пропорционально делить и получаем, скажем так, нормальную громкость человеческой речи: 80 / φ = 50 децибел.
Ну, а последний звук, который получим благодаря формуле – приятный звук шепота = 2,618.

По данному принципу можно определить оптимально-комфортное, минимальное и максимальное число температуры, давления, влажности. Я не проверяла, и не знаю, насколько эта теория верна, но, согласитесь, звучит впечатляюще.

Главное, только не увлекаться этим, ведь если мы хотим что-то в чем-то увидеть, то увидим, даже если этого там нет

Вот я, например, обратила внимание на дизайн PS4 и увидела там золотое сечение =) Впрочем, эта консоль настолько классная, что не удивлюсь, если дизайнер, и правда, что-то там мудрил

Золотое сечение в искусстве

Тоже очень большая и обширная тема, которую стоит рассмотреть отдельно. Тут лишь помечу несколько базовых моментов. Самое примечательное, что многие произведения искусства и архитектурные шедевры древности (и не только) сделаны, по принципам золотого сечения.

Египетские и пирамиды Майя, Нотр-дам де Пари, греческий Парфенон и так далее.
В музыкальных произведениях Моцарта, Шопена, Шуберта, Баха и прочих.
В живописи (там это наглядно видно): все самые знаменитые картины известных художников сделаны с учетом правил золотого сечения.
Эти принципы можно встретить и в стихах Пушкина, и в бюсте красавицы Нефертити.
Даже сейчас правила золотой пропорции используются, например, в фотографии. Ну, и конечно, во всем остальном искусстве, включая кинематограф и дизайн.

https://youtube.com/watch?v=c3SVIQBXMnA

Расчет основных параметров двигателя с шильдика

Электродвигатели встречаются в промышленности и быту повсеместно

Если Вы не обращали внимание, то я приведу парочку фото примеров:

Порой возникает необходимость, рожденная будничным любопытством, либо производственной необходимостью в определении мощности электродвигателя по внешнему виду, или значения допустимой температуры в эксплуатации, не говоря уже о значениях тока и напряжения.

Тут возможен вариант, что с него содрана табличка, на которой написаны номинальные параметры, либо же шильдик в таком состоянии, что различить ничего невозможно. Как же быть в такой ситуации…

Одно дело, если Вы всю жизнь работали на производстве движков, и можете определить мощность на глаз. В иных случаях, определить поможет линейка (рулетка) и таблицы с габаритами механизмов.

Если Ваша деятельность больше лежит в теоретических изысканиях, нежели практических, то пригодится формула определения мощности ЭД или таблицы с номинальным данными, именно про это и не только в этой статье.

О коэффициенте мощности в сетях переменного тока и его влиянии на потребителей