ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. В катушку, соединённую с гальванометром, вносят магнит. Направление индукционного тока зависит
А. От скорости перемещения магнита. Б. От того, каким полюсом вносят магнит в катушку.
Правильный ответ
1) только А 2) только Б 3) и А, и Б 4) ни А, ни Б
2. В катушку, соединённую с гальванометром, вносят магнит. Сила индукционного тока зависит
А. от скорости перемещения магнита Б. от того, каким полюсом вносят магнит в катушку
1) только А 2) только Б 3) и А, и Б 4) ни А, ни Б
3. Постоянный магнит вносят в катушку, замкнутую на гальванометр (см. рисунок).
Если выносить магнит из катушки с большей скоростью, то показания гальванометра будут примерно соответствовать рисунку
4. Две одинаковые катушки замкнуты на гальванометры. В катушку А вносят полосовой магнит, а из катушки Б вынимают такой же полосовой магнит. В какой катушке гальванометр зафиксирует индукционный ток?
1) только в катушке А 2) только в катушке Б 3) в обеих катушках 4) ни в одной из катушек
5. В первом случае магнит вносят в сплошное эбонитовое кольцо, а во втором случае выносят из сплошного медного кольца (см. рисунок).
Индукционный ток
1) возникает только в эбонитовом кольце 2) возникает только в медном кольце 3) возникает в обоих кольцах 4) не возникает ни в одном из колец
6. Внутри катушки, соединённой с гальванометром, находится малая катушка, подключённая к источнику постоянного тока. В каком из перечисленных опытов гальванометр зафиксирует индукционный ток?
А. В малой катушке выключают электрический ток. Б. Малую катушку вынимают из большой.
1) только в опыте А 2) только в опыте Б 3) в обоих опытах 4) ни в одном из опытов
7. Внутри катушки, соединённой с гальванометром, находится малая катушка, подключённая к источнику тока. Первую секунду от начала эксперимента малая катушка неподвижна внутри большой катушки. Затем в течение следующей секунды её вынимают из большой катушки. Третью секунду малая катушка находится вне большой катушки. В течение четвертой секунды малую катушку вдвигают в большую. В какой(-ие) промежуток(-ки) времени гальванометр зафиксирует появление индукционного тока?
1) только 0-1 с 2) 1 с-2 с и 3 с-4 с 3) 0-1 с и 2 с-3 с 4) только 1 с-2 с
8. Внутри катушки, соединённой с гальванометром, находится малая катушка, подключённая к источнику тока. Оси катушек совпадают. Первую секунду от начала эксперимента малая катушка неподвижна внутри большой катушки. Затем в течение следующей секунды её вращают относительно вертикальной оси по часовой стрелке. Третью секунду малая катушка вновь остаётся в покое. В течение четвёртой секунды малую катушку вращают против часовой стрелки. В какие промежутки времени гальванометр зафиксирует появление индукционного тока в катушке?
1) индукционный ток может возникнуть в любой промежуток времени 2) индукционный ток возникнет в промежутках времени 1-2 с, 3-4 с 3) индукционный ток не возникнет ни в какой промежуток времени 4) индукционный ток возникнет в промежутках времени 0-1 с, 2-3 с
9. К электромагнитным волнам относятся:
A. Волны на поверхности воды. Б. Радиоволны. B. Световые волны.
Укажите правильный ответ.
1) только А 2) только Б 3) только В 4) Б и В
10. Какие из приведённых ниже формул могут быть использованы для определения скорости электромагнитной волны?
A. \( v=\lambda\nu \) Б. \( v=\frac{\lambda}{\nu} \) В. \( v=\frac{\lambda}{T} \) Г. \( v=\lambda T \)
1) только А 2) только Б 3) А и В 4) В и Г
11. Установите соответствие между названием опыта (в левом столбце таблицы) и явлением, которое в этом опыте наблюдается (в правом столбце таблицы). В таблице под номером физической величины левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.
ВЕЛИЧИНА A) опыты Фарадея Б) опыт Эрстеда B) опыт Ампера
ХАРАКТЕР ИЗМЕНЕНИЯ ЗНАЧЕНИЯ ВЕЛИЧИНЫ 1) действие проводника с током на магнитную стрелку 2) электромагнитная индукция 3) взаимодействие проводников с током
12. Установите соответствие между техническими устройствами и физическими явлениями, лежащими в основе их работы.
ТЕХНИЧЕСКИЕ УСТРОЙСТВА A) генератор электрического тока Б) электрический двигатель B) электромагнитное реле
ФИЗИЧЕСКИЕ ЯВЛЕНИЯ 1) взаимодействие постоянных магнитов 2) взаимодействие проводников с током 3) возникновение электрического тока в проводнике при его движении в магнитном поле 4) магнитное действие проводника с током 5) действие магнитного поля на проводник с током
Часть 2
13. На какую частоту нужно настроить радиоприёмник, чтобы слушать радиостанцию, которая передает сигналы па длине волны 2,825 м?
1) 106,2 кГц 2) 106,2 МГц 3) 847,5 кГц 4) 847,5 МГц
Регулирование частоты вращения ДПТ НВ изменение напряжения в цепи якоря
Регулирование частоты вращения двигателя изменением питающего напряжения применяется лишь при IB = const, т. е. при раздельном питании цепей обмотки якоря и обмотки возбуждения при независимом возбуждении.
Частота вращения в режиме х.х. n пропорциональна напряжению, а
в
Для управления двигателями большой мощности целесообразно применять генератор постоянного тока независимого возбуждения; привод осуществляется посредством приводного двигателя (ПД), в качестве которого обычно используют трехфазный двигатель переменного тока. Для питания постоянным током цепей возбуждения генератора Г и двигателя Д используется возбудитель В — генератор постоянного тока, напряжение на выходе которого поддерживается неизменным. Описанная схема управления двигателем постоянного тока (рис. 29.6, б) известна под названием системы «генератор — двигатель» (Г—Д).
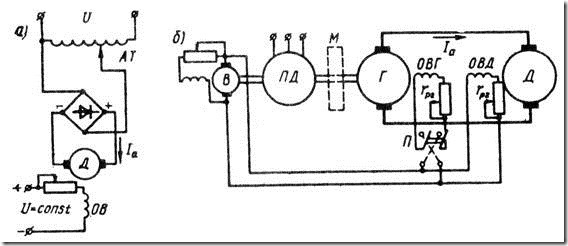
Рис. 29.6. Схемы включения двигателей постоянного тока при регулировании частоты вращения изменением напряжения в цепи якоря
Изменение напряжения в цепи якоря позволяет регулировать частоту вращения двигателя вниз от номинальной, так как напряжение свыше номинального недопустимо. При необходимости регулировать частоту вращения вверх от номинальной можно воспользоваться изменением тока возбуждения двигателя.
Изменение направления вращения (реверс) двигателя, работающего по системе Г—Д, осуществляется изменением направления тока в цепи возбуждения генератора Г переключателем П, т. е. переменой полярности напряжения на его зажимах. Если двигатель постоянного тока работает в условиях резко переменной нагрузки, то для смягчения колебаний мощности, потребляемой ПД из трехфазной сети, на вал ПД помещают маховик М, который запасает энергию в период уменьшения нагрузки на двигатель Д и отдает ее в период интенсивной нагрузки двигателя.
Регулирование частоты вращения изменением напряжения в цепи якоря обеспечивает плавное экономичное регулирование в широком диапазоне nMAX/nMIN ≥ 25 . Наибольшая частота вращения здесь ограничивается условиями коммутации, а наименьшая — условиями охлаждения двигателя.
Еще одним достоинством рассматриваемого способа регулирования является то, что он допускает безреостатный пуск двигателя при пониженном напряжении.
Конвертер величин
Калькуляторы
В этой части Конвертера физических единиц TranslatorsCafe.com представлена группа калькуляторов, выполняющих расчеты в различных областях электротехники, радиотехники и электроники.
Магнитостатика, магнетизм и электродинамика
Магнитостатика — раздел классической электродинамики, изучающий взаимодействие постоянных токов посредством создаваемого ими постоянного магнитного поля и способы расчета магнитного поля в этом случае.
Электродинамика
— раздел физики, изучающий силы, возникающие при взаимодействии электрически заряженных частиц и тел. Эти силы объясняются в электродинамике с помощью электромагнитных полей. Силы электромагнитного взаимодействия лежат в основе большинства явлений, с которыми мы встречаемся в повседневной жизни. Часть привычных явлений обусловлена действием гравитационных сил.
Электромагнитное поле
— физическое поле, появляющееся при взаимодействии движущихся заряженных телами или частиц. Электромагнитное поле можно рассматривать как сочетание электрического и магнитного полей.
Электрическое поле
— физическое поле, окружающее электрически заряженные частицы, проводники с проходящими в них электрическими токами и изменяющиеся во времени и пространстве магнитные поля.
Магнитное поле
— физическое силовое поле, окружающее заряженные частицы, проводники с электрическим током, магнитные материалы и переменные электрические поля, а также действующее на проводники с электрическим током, движущиеся электрические заряды и тела, обладающие магнитным моментом. Магнитное поле в любой точке определяется направлением и силой и таким образом является векторным полем. Магнитное поле характеризуется двумя основными величинам — вектором магнитной индукцииВ и вектором напряженности магнитного поляH .
Конвертер магнитного потока
Магнитный поток
определяется как интеграл вектора магнитной индукции через конечную поверхность. Также магнитный поток можно рассчитать как скалярное произведение вектора магнитной индукции на вектор площади. Для измерения магнитного потока используют флюксметр, который измеряет напряжение на измерительной катушке.
В СИ единицей магнитного потока является вебер
(Вб, размерность — В·с = кг·м²·с⁻²·А⁻¹). Магнитный поток, равный 1 Вб, создается магнитным полем с индукцией 1 Тл, пронизывающим по направлению нормали плоский контур площадью 1 м². В системе СГС — магнитный поток измеряется вмаксвеллах (Мкс).
Использование конвертера «Конвертер магнитного потока»
На этих страницах размещены конвертеры единиц измерения, позволяющие быстро и точно перевести значения из одних единиц в другие, а также из одной системы единиц в другую. Конвертеры пригодятся инженерам, переводчикам и всем, кто работает с разными единицами измерения.
Изучайте технический английский язык и технический русский язык с нашими видео! — Learn technical English and technical Russian with our videos!
Пользуйтесь конвертером для преобразования нескольких сотен единиц в 76 категориях или несколько тысяч пар единиц, включая метрические, британские и американские единицы. Вы сможете перевести единицы измерения длины, площади, объема, ускорения, силы, массы, потока, плотности, удельного объема, мощности, давления, напряжения, температуры, времени, момента, скорости, вязкости, электромагнитные и другие. Примечание.
В связи с ограниченной точностью преобразования возможны ошибки округления. В этом конвертере целые числа считаются точными до 15 знаков, а максимальное количество цифр после десятичной запятой или точки равно 10.
Для представления очень больших и очень малых чисел в этом калькуляторе используется компьютерная экспоненциальная запись
, являющаяся альтернативной формой нормализованной экспоненциальной (научной) записи, в которой числа записываются в форме a · 10x. Например: 1 103 000 = 1,103 · 106 = 1,103E+6. Здесь E (сокращение отexponent ) — означает «· 10^», то есть«…умножить на десять в степени…» . Компьютерная экспоненциальная запись широко используется в научных, математических и инженерных расчетах.
Мы работаем над обеспечением точности конвертеров и калькуляторов TranslatorsCafe.com, однако мы не можем гарантировать, что они не содержат ошибок и неточностей. Вся информация предоставляется «как есть», без каких-либо гарантий. Условия.
Если вы заметили неточность в расчётах или ошибку в тексте, или вам необходим другой конвертер для перевода из одной единицы измерения в другую, которого нет на нашем сайте — напишите нам!
Канал Конвертера единиц TranslatorsCafe.com на YouTube
Измерительные приборы
Индукция магнитного поля
Магнитные потоки, определимые с помощью специальных приборов – флюксметров, измеряются и в лабораторных, и в полевых условиях. Приборы ещё называют веберметрами. Особенностью такого измерительного аппарата магнитоэлектрической системы (МЭС) является то, что ток подводится к перемещающейся бескаркасной рамке через спирали, не имеющие момента противодействия (безмоментные).
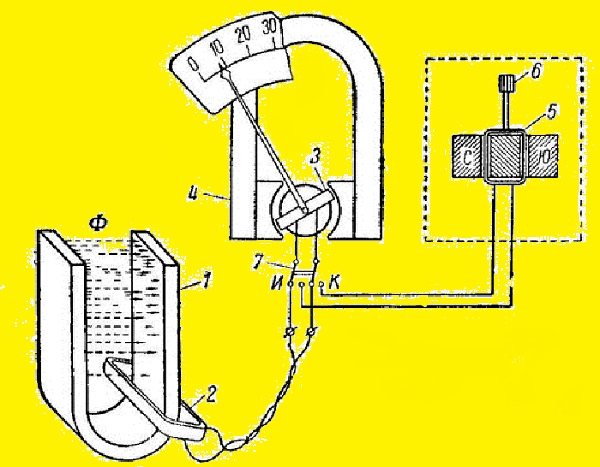
Схема применения и устройства флюксметра
Прибор состоит из следующих деталей, отмеченных на рис. выше:
- испытуемый постоянный магнит – 1;
- рамка измерительная – 2;
- рамка прибора – 3;
- магнит прибора – 4;
- рамка корректирующего устройства – 5;
- головка регулировки корректирующей рамки – 6;
- переключатель «работа – коррекция» – 7.
Флюксметр не может измерять слабые МП из-за низкой чувствительности.
Закон электромагнитной индукции
Закон электромагнитной индукции (закон Фарадея) звучит так:
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром.
Математически его можно описать формулой:
Закон Фарадея
Ɛi — ЭДС индукции
ΔФ/Δt — скорость изменения магнитного потока [Вб/с]
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре всегда направлен так, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из N витков (то есть он — катушка), то ЭДС индукции будет вычисляться следующим образом.
Закон Фарадея для контура из N витков
Ɛi — ЭДС индукции
ΔФ/Δt — скорость изменения магнитного потока [Вб/с]
N — количество витков
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением R:
Закон Ома для проводящего контура
Ɛi — ЭДС индукции
I — сила индукционного тока
R — сопротивление контура
Если проводник длиной l будет двигаться со скоростью v в постоянном однородном магнитном поле с индукцией B ЭДС электромагнитной индукции равна:
ЭДС индукции для движущегося проводника
Ɛi — ЭДС индукции
B — магнитная индукция
v — скорость проводника [м/с]
l — длина проводника
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле
- вследствие изменения во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Причины возникновения индукционного тока в движущихся и неподвижных проводниках
Причин, по которым может происходить изменение магнитного потока, пронизывающего замкнутый контур, две:
- Изменение магнитного потока вследствие перемещения всего контура или отдельных его частей в магнитном поле, которое не изменяется со временем;
- Изменение магнитного поля при неподвижном контуре.
Перейдем к рассмотрению этих случаев подробнее.
Перемещение контура или его частей в неизменном магнитном поле
При движении проводников и свободных носителей заряда в магнитном поле возникает ЭДС индукции. Объяснить возникновение δинд можно действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца здесь – это сторонняя сила.
Пример 2
На рисунке мы изобразили пример индукции, когда прямоугольный контур помещен в однородное магнитное поле B→ направленное перпендикулярно плоскости контура. Одна из сторон контура перемещается по двум другим сторонам с некоторой скоростью.
Рисунок 1.20.3. Возникновение ЭДС индукции в движущемся проводнике. Отражена составляющая силы Лоренца, которая действует на свободный электрон
На свободные заряды подвижной части контура воздействует сила Лоренца. Основная составляющая силы Лоренца в данном случае направлена вдоль проводника и связана с переносной скоростью зарядов υ→. Модуль этой сторонней силы равен:
FЛ=eυ→B.
Работа силы FЛ на пути l равна:
A=FЛ·l=eυBl.
По определению ЭДС:
δинд=Ae=υBl.
Значение сторонней силы для неподвижных частей контура равно нулю. Для соотношения δинд можно записать другой вариант формулы. Площадь контура с течением времени изменяется на ΔS=lυΔt. Соответственно, магнитный поток тоже будет с течением времени изменяться: ΔΦ=BlυΔt.
Следовательно,
δинд=∆Φ∆t.
Знаки в формуле, которая связывает δинд и ∆Φ∆t, можно установить в зависимости от того, какие направления нормали и направления контура будут выбраны. В случае выбора согласованных между собой по правилу правого буравчика направлений нормали n→ и положительного направления обхода контура l→ можно прийти к формуле Фарадея.
При условии, что сопротивление всей цепи – это R, то по ней будет протекать индукционный ток, который равен Iинд=δиндR. За время Δt на сопротивлении R выделится джоулево тепло:
∆Q=RIинд2∆t=υ2B2l2R∆t
Парадокса здесь нет. Мы просто не учли воздействие на систему еще одной силы. Объяснение заключается в том, что при протекании индукционного тока по проводнику, расположенному в магнитном поле, на свободные заряды действует еще одна составляющая силы Лоренца, которая связана с относительной скоростью движения зарядов вдоль проводника. Благодаря этой составляющей появляется сила Ампера FА→.
Для рассмотренного выше примера модуль силы Ампера равен FA =IBl. Направление силы Ампера таково, что она совершает отрицательную механическую работу Aмех. Вычислить эту механическую работу за определенный период времени можно по формуле:
Aмех=-Fυ∆t=-IBlυ∆t=-υ2B2l2R∆t
Проводник, перемещающийся в магнитном поле, испытывает магнитное торможение. Это приводит к тому, что полная работа силы Лоренца равна нулю. Джоулево тепло может выделяться либо за счет уменьшения кинетической энергии движущегося проводника, либо за счет энергии, которая поддерживает скорость перемещения проводника в пространстве.
Изменение магнитного поля при неподвижном контуре
Определение 3
Вихревое электрическое поле – это электрическое поле, которое вызывается изменяющимся магнитным полем.
В отличие от потенциального электрического поля работа вихревого электрического поля при перемещении единичного положительного заряда по замкнутому проводящему контуру равна δинд в неподвижном проводнике.
В неподвижном проводнике электроны могут приводиться в движение только под действием электрического поля. А возникновение δинд нельзя объяснить действием силы Лоренца.
Первым, кто ввел понятие вихревого электрического поля, был английский физик Джон Максвелл. Случилось это в 1861 году.
Фактически, явления индукции в подвижных и неподвижных проводниках протекают одинаково. Так что в этом случае мы тоже можем использовать формулу Фарадея. Отличия касаются физической причины возникновения индукционного тока: в движущихся проводниках δинд обусловлена силой Лоренца, в неподвижных – действием на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Рисунок 1.20.4. Модель электромагнитной индукции
Рисунок 1.20.5. Модель опытов Фарадея
Рисунок 1.20.6. Модель генератора переменного тока
Всё ещё сложно?
Наши эксперты помогут разобраться
Все услуги
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Электромагнитная индукция в движущемся проводнике
Эксперименты показывают, что ЭДС индукции возникает в любом отрезке проводника, движущемся в магнитном поле и пересекающем линии магнитной индукции. ЭДС индукции в таком «микрогенераторе» можно рассчитать с помощью схемы, представленной на Рис.1. По параллельным металлическим «рельсам», замкнутым с одной стороны проводящей перемычкой AB, в однородном поле с магнитной индукцией B с постоянной скоростью v скользит проводящий «мостик» CD длиной l . За время dt магнитный поток, пронизывающий контур ABCD, возрастает на величину dФ = Bvl·dt, откуда
Согласно основному закону электромагнитной индукции ЭДС, индуктируемая в контуре, определяется соотношением
Так как все элементы контура, кроме «мостика», неподвижны относительно магнитного поля, то (2) — это и есть ЭДС, возникающая в движущемся проводнике.
Эта же ЭДС возникает и в незамкнутом проводящем отрезке, движущемся в магнитном поле (Рис. 2). Считается, что при перемещении проводящего отрезка в магнитном поле силой, «разделяющей» заряды q в проводнике и создающей на концах такого «микрогенератора» индукционную ЭДС, является магнитная составляющая силы Лоренца:
Если скорость движения проводника постоянна, то и ЭДС индукции остается постоянной. В момент остановки заряды в проводнике под действием кулоновских сил «схлопываются» и микрогенератор практически мгновенно разряжается.
ЭДС в таком индукционном микрогенераторе возникает вследствие того, что проводник пересекает линии магнитного поля с некоторой скоростью v. Назовем (для краткости) такой способ генерации ЭДС электромагнитной индукции «способом пересечения». Процесс электромагнитной индукции «с пересечением» можно схематически представить так:
пересечение → возникновение силы Лоренца → перемещение зарядов → образование ЭДС
ЭДС индукции
где Ei – ЭДС индукции, возникающая в контуре при равномерном изменении магнитного потока (В); ΔΦ = Φ2 — Φ1 – изменение магнитного потока от Φ1 до Φ2 (Вб); Δt – время изменения магнитного потока (с); ΔΦ/Δt – скорость изменения магнитного потока (Вб/с или В).
- Эту формулу можно применять только при равномерном изменении магнитного потока.
- При увеличении магнитного потока (ΔΦ > 0), ЭДС отрицательная (ℰi < 0), т.е. индукционный ток имеет такое направление, что вектор магнитной индукции индукционного магнитного поля направлен против вектора магнитной индукции внешнего (изменяющегося) магнитного поля (рис. 2 а).
- При уменьшении магнитного потока (ΔΦ < 0), ЭДС положительная (Ei > 0), т.е. индукционный ток имеет такое направление, что вектор магнитной индукции индукционного магнитного поля направлен в одну и ту же сторону с вектором магнитной индукции внешнего (изменяющегося) магнитного поля (рис. 2 б).
- Знак «–» в формуле будем учитывать в задачах, где указано как изменяется (увеличивается или уменьшается) магнитный поток.
Так как магнитный поток равен \(~\Phi = B \cdot S \cdot \cos \alpha\) , то он может изменяться:
- или только за счет изменения магнитной индукции поля, тогда
-
\(~\Delta \Phi = (B_2 — B_1) \cdot S \cdot \cos \alpha\) ;
-
- или только за счет изменения площади контура, тогда
-
\(~\Delta \Phi = B \cdot (S_2 — S_1) \cdot \cos \alpha\) ;
-
- или только за счет поворота контура в магнитном поле, тогда
-
\(~\Delta \Phi = B \cdot S \cdot (\cos \alpha_2 — \cos \alpha_1)\) ;
-
- или одновременно за счет изменения нескольких параметров, тогда
-
\(~\Delta \Phi = B_2 \cdot S_2 \cdot \cos \alpha_2 — B_1 \cdot S_1 \cdot \cos \alpha_1\) .
-
При любом способе изменения магнитного потока в контуре возникает ЭДС индукции.
Индукционный ток
где Ii – индукционный ток в контуре (А), Ei – ЭДС индукции (В), R – сопротивление контура (Ом).
План определения направления индукционного тока:
- Установите направление вектора магнитной индукции внешнего поля (\(~\vec B\)).
- Выясните, как изменяется (увеличивается или уменьшается) поток магнитной индукции этого поля через поверхность контура.
- Используя правило Ленца, установите направление вектора магнитной индукции индукционного магнитного поля (\(~\vec B_i\)) :
- если поток магнитной индукции через контур увеличивается, то вектор магнитной индукции индукционного магнитного поля (\(~\vec B_i\)) направлен в противоположную сторону вектора магнитной индукции внешнего поля (\(~\vec B\)) ;
- если поток магнитной индукции через контур уменьшается, то вектор магнитной индукции индукционного магнитного поля (\(~\vec B_i\)) направлен в ту же сторону, что и вектор магнитной индукции внешнего поля (\(~\vec B\)) .
- Используя правило правой руки, по направлению вектора магнитной индукции индукционного магнитного поля (\(~\vec B_i\)) найдите направление индукционного тока.
ЭДС индукции движущегося проводника
Индукционный ток в проводниках, движущихся в магнитном поле, возникает за счет действия на свободные заряды проводника силы Лоренца. Поэтому направление индукционного тока в проводнике будет совпадать с направлением составляющей силы Лоренца на этот проводник.
С учетом этого можно сформулировать следующее правило левой руки для определения направления индукционного тока в движущемся проводнике: нужно расположить левую руку так, чтобы вектор магнитной индукции входил в ладонь, четыре пальца совпадали с направлением движения проводника, тогда отставленный на 90° большой палец укажет направление индукционного тока (рис. 3).
- Если проводник движется вдоль вектора магнитной индукции, то индукционного тока не будет (сила Лоренца равна нулю).
- Ток не может идти поперек проводника (заряды под действием силы Лоренца смещаются к стенкам проводника и создавать ток не будут) (рис. 4).
где Ei – ЭДС индукции движущегося проводника (В); υ – скорость движения проводника (м/с); В – модуль вектора магнитной индукции (Тл); l – длина проводника (м); α – угол между направлением движения проводника и вектором магнитной индукции.
Линии напряженности магнитного поля
Магнитное поле не влияет на неподвижный заряд, действует на движущееся электричество. Когда Био экспериментально, Савар позже математически сформулировали закон, понадобились модели, описывающие взаимодействие нового явления с объектами материального мира. Следует четко понимать, хотя закон Био-Савара содержит величину магнитной индукции, на момент 1820 года попросту отсутствовала в научной сфере. Некая мера поля, что именно представляла, никто в точности сказать не мог. Гауссова СГС появилась в 1832 году, лишена многих физических величин.
Трактат 1600 года Гильберта высказал предположение о структуре линий напряженности. Для выяснения обстоятельств активно использовал магнитную стрелку, создал шар руды, доказал подобие поля объекта Земному. По характеру взаимодействия выдвинул идею: один полюс испускает некую субстанцию, другой – поглощает. Довольствуясь доводами, Рене Декарт в 1644 году создал одну из первых картин магнитного поля, использовав мелкие металлические опилки. Опытом не брезгают сегодняшние учебники физики. Линии напряженности магнитного поля являются плавными, замыкаются на полюсах, вектор индукции направлен касательно в каждой точке.
Сообразно закону Био-Савара, имеющимся знаниям Пуассон в 1824 году создает первую модель поля. Оперирует с диполями, отстраняется от среды распространения явления. Ампер идет иным путем, представляя источники магнитного поля, элементарными циркулирующими зарядами. Проводя опыты, замечает: сила взаимодействия зависит от среды, вносит таким образом лепту. Правы оказались оба.
Магнитное поле планеты Земля
Существование магнитного поля независимо от среды, сила действия на объекты в некоторых материалах изменяется. Для описания количественной меры изменения ввели единицу относительной магнитной проницаемости. Показывает отличие силы взаимодействия в сравнении с процессом, идущим в вакууме. Согласно такому подходу, материалы формируют три группы:
- Парамагнетики немного усиливают напряженность Н, индукция магнитного поля немного больше, нежели в вакууме. Вещества теряют приобретенные в результате взаимодействия свойства так скоро, как пропадает источник изменений.
- Диамагнетики ослабляют действие поля. Напряженность Н выше индукции В. Класс веществ включает: поваренную соль, нафталин, висмут. Поле ослабляется, магнитная восприимчивость отрицательная.
- Ферромагнетики многократно усиливают напряженность, индукция намного превышает H. По этой причине идут на изготовление сердечников трансформаторов.
Теперь поясним: напряженность поля H характеризует свойства источника магнетизма, существует в любой среде. Индукция показывает способность явления индуцировать в проводниках ЭДС. Откуда произошло название. Хотя на практике индукция играет первостепенную роль, рассмотрение случаев с одновременным использованием разных сред удобно вести с позиций напряженности поля. Значение домножается величиной магнитной проницаемости среды.
Кстати, Майкл Фарадей, не зная фактов, выбрал для удачного опыта с тороидальным трансформатором ферромагнетик (мягкая сталь). Благодаря этому удачно удалось зафиксировать явление индукции. Оно имеет место быть в воздухе, но не так заметно. Ферромагнетик умножает многократно способность поля индуцировать отклик в виде ЭДС вторичной обмотки трансформатора. Коэффициент проницаемости некоторых материалов составляет тысячи единиц.
Законы, связанные с магнитной индукцией
На чертежах условились линии магнитного поля наносить тем плотнее, чем выше индукция. На единицу площади (например, квадратный сантиметр) приходится столько, каково значение физической величины в Тл. Помогает визуально оценить плотность поля. Количество линий, охваченных площадью фигуры, отражает величину работы по перемещению в пределах нее электрического заряда. Тезис отражен законом Фарадея (см. рис.), где фигурирует величина плотности магнитной индукции, измеряемой веберами.
Как изменить магнитный поток
Формула (6) показывает лишь связь между электромагнитными процессами в дросселе, но не предусматривает возможности изменения ни токов в обмотках, ни магнитного потока. И значит, пришло время вспомнить открытый Фарадеем закон электромагнитной индукции, связывающий электродвижущую силу е с изменением магнитного потока:
| (9) |
где N – количество витков обмотки.
Подобно рассмотренной выше теореме о циркуляции вектора напряженности магнитного поля, закон Фарадея также связывает две части единого целого. Закон электромагнитной индукции работает «в обе стороны»: любое изменение магнитного потока, например, из-за перемещения постоянного магнита возле обмотки, приводит к появлению на ее выводах ЭДС, а появление стороннего напряжения на выводах – к изменению магнитного потока. Таким образом, прикладывая к обмотке произвольное напряжение u(t) на протяжении некоторого интервала времени tНАЧ. tКОН можно изменить магнитный поток на величину ΔФ:
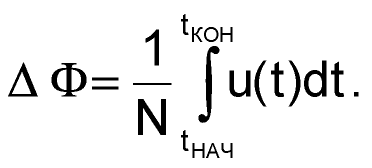 |
(10) |
На протяжении первого этапа преобразования к обмотке W1 через открытый ключ S1 прикладывается напряжение конденсатора С1, равное напряжению на входе преобразователя UВХ. Для обеспечения нормальной работы схемы количество энергии в конденсаторах С1 и С2 должно быть как минимум на порядок больше количества энергии, накапливаемой в дросселе L1. Это означает, что изменением напряжения на конденсаторе С1 за время первого этапа преобразования можно пренебречь, приняв uW1(t) = UВХ = const. Это позволяет вынести uW1(t) в формуле (10) за знак интеграла и определить величину изменения магнитного потока на первом этапе преобразования ΔФ1:
| (11) |
где t1 – длительность первого этапа преобразования.
Таким образом, к следующей коммутации ключей S1 и S2 магнитный поток станет равным ФКОН1 = ФНАЧ1 + ΔФ1, которому будет соответствовать ток IW1_КОН в обмотке W1:
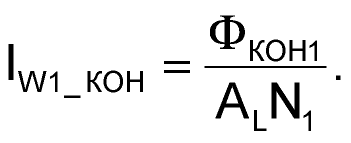 |
(12) |
После окончания первого этапа преобразования, начинается второй, на протяжении которого ключ S1 находится в разомкнутом, а ключ S2 – в замкнутом состоянии. Очевидно, что все процессы на втором этапе полностью идентичны и отличаются только активными элементами схемы: дроссель L1 через обмотку W2 и ключ S2 обменивается энергией с конденсатором С2, а элементы С1, W1 и S1 не принимают участия в работе. Как и на первом этапе, в момент замыкания ключа S2 магнитный поток ФНАЧ2 в дросселе может быть отличен от нуля, и ему будет соответствовать ток IW2_НАЧ в обмотке W2:
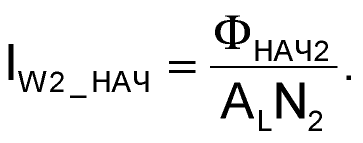 |
(13) |
Точно так же, за время второго этапа магнитный поток изменится на величину ΔФ2, поскольку к его обмотке W2 через открытый ключ S2 приложено напряжение uW2(t), равное напряжению на конденсаторе С2, которое на протяжении второго этапа длительностью t2 практически не меняется, и значит его можно считать постоянным и равным выходному напряжению преобразователя UВЫХ, поэтому
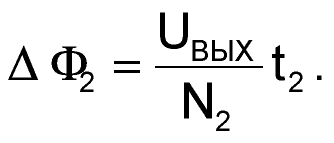 |
(14) |
А к концу второго этапа магнитный поток достигнет величины ФКОН2 = ФНАЧ2 + ΔФ2, которому будет соответствовать ток IW2_КОН:
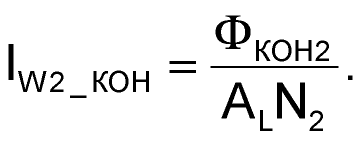 |
(15) |
Поскольку в моменты коммутации ключей S1 и S2 магнитный поток Ф остается неизменным, мы имеем полное право записать:
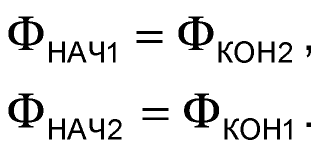 |
(16) |
Ну и для того, чтобы преобразователь выполнял свою непосредственную функцию, должно выполняться последнее условие:
| (17) |
иначе магнитопровод дросселя после нескольких циклов достигнет насыщения, его параметр AL за счет уменьшения μЭКВ уменьшиться, а токи обмоток, определяемые (8), (12), (13) и (15) резко возрастут, что приведет к перегрузке и выходу из строя силовых элементов. Да и схема работать не будет, поскольку при совпадении знаков ΔФ1 и ΔФ2 магнитопровод дросселя, будет только накапливать энергию.