Как перевести из одной системы в другую
На бумаге степень способа счисления обозначается нижним индексом после крайнего правого значения. В математике субскрипты используются нечасто в отличие от химии. Каждая формула содержит различные индексы нижнего и верхнего регистра.
Существует два способа осуществить перевод из двоичной системы в десятичную:
- позиционная нотация;
- удвоение.
Разбор перевода позиционной нотацией будет происходить на примере числа 10011011.
Первый шаг, чтобы произвести перевод числа из двоичной системы в десятичную — возведение всех чисел выражения в степень. Степень с каждым шагом увеличивается на 1, начинается с 0 справа налево. Выглядит это таким образом: 18 07 06 15 14 03 11 1. После преобразований получается числовой ряд 128, 64, 32, 16, 8, 4, 2, 1, сопоставляется с начальным 10011011.
Каждое число из возведенного в степень примера умножается на цифру примера 10011011 по порядку. Таким образом, 128 умножается на 1, 64 — на 0, 32 — на 0 и т.д. В итоге вычитаются все нулевые значения и остается 128, 16, 8, 2, 1. Для получения ответа в десятичной системе все цифры суммируются. Результат — 155.
Перевод методом удвоения проще для преобразования в уме или на бумаге. Этот способ перевода не использует математические функции со степенями, а только суммирование и простое умножение.
Способ подразумевает суммирование всех результатов, основываясь на многочлене a х 0 + b, где b равняется текущему значению, а — предыдущему. Эта функция применяется для каждого знака ряда 10011011. Для получения первого результата, следует исходить из утверждения, что предыдущее значение перед первой цифрой равняется 0. Следуя из этого, после подставления данных образовывается многочлен 0 х 2 + 1 и дает ответ — 1. Для второй цифры 0 получается многочлен 1 х 2 + 0, ответ — 2. Для третьего знака 0 — многочлен 2 х 2 + 0, ответ, соответственно, 4. Сумма равняется результату перевода в десятичной системе.
Перевод дробного десятичного числа в q-ичную систему
Для того чтобы перевести десятичное число, содержащее дробную часть, необходимо отдельно перевести целую часть и отдельно дробную.
Пример 5: перевести число 358,201 из десятичной системы в шестиричную
Для решения примера потребуется отдельно перевести 358 и отдельно 0,201 из десятичной системы в шестиричную, используя вышеизложенные алгоритмы. Таким образом переведя 358, получим:
35810=13546
Перевод десятичной дроби 0,201 выглядит так:
0.201 ∙ 6 = 1.206 (1) 0.206 ∙ 6 = 1.236 (1) 0.236 ∙ 6 = 1.416 (1) 0.416 ∙ 6 = 2.496 (2) 0.496 ∙ 6 = 2.976 (2) 0.976 ∙ 6 = 5.856 (5) 0.856 ∙ 6 = 5.136 (5) 0.136 ∙ 6 = 0.816 (0) 0.816 ∙ 6 = 4.896 (4) 0.896 ∙ 6 = 5.376 (5) 0.376 ∙ 6 = 2.256 (2)
0.20110=0.111225504526
Теперь осталось соединить результаты перевода. Таким образом: 358.20110=1354.111225504526
4.1. Что такое система счисления?
|
Система счисления — это способ записи чисел с помощью заданного набора специальных знаков (цифр). |
Существуют позиционные и непозиционные системы счисления.
В непозиционных системах вес цифры (т.е. тот вклад,
который она вносит в значение числа) не зависит от ее позиции в записи
числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х
в любой позиции равен просто десяти.
В позиционных системах счисления вес каждой цифры
изменяется в зависимости от ее положения (позиции) в последовательности
цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7
сотен, вторая – 7 единиц, а третья – 7 десятых долей единицы.
Сама же запись числа 757,7 означает сокращенную запись выражения
700 + 50 + 7 + 0,7 = 7•102 + 5•101 + 7•10 +
7•10-1 = 757,7.
Любая позиционная система счисления характеризуется своим основанием.
|
Основание позиционной системы счисления — это количество различных знаков или символов, используемых для изображения цифр в данной системе. |
За основание системы можно принять любое натуральное число — два, три, четыре
и т.д. Следовательно, возможно бесчисленное множество позиционных систем:
двоичная, троичная, четверичная и т.д. Запись чисел в каждой из систем счисления
с основанием q означает сокращенную запись выражения
an-1 qn-1 + an-2 qn-2+ …
+ a1 q1 + a q + a-1
q-1 + … + a-m q-m,
где ai – цифры системы счисления; n и
m – число целых и дробных разрядов, соответственно.
Например:
Преобразование двоичного числа в дополнительном коде в десятичную форму
Чтобы преобразовать двоичное число в дополнительном коде обратно в десятичную форму, сначала посмотрите на бит знака.
Если бит знака равен 0, просто преобразуйте число, как было показано выше для чисел без знака.
Если бит знака равен 1, мы инвертируем биты, добавляем 1, затем выполняем преобразование в десятичное число, а затем делаем это десятичное число отрицательным (поскольку бит знака изначально был отрицательным).
Например, чтобы преобразовать 1001 1110 в дополнительном коде в десятичное число:
- дано: 1001 1110
- инвертируем биты: 0110 0001
- добавляем 1: 0110 0010
- преобразуем в десятичную форму:(0 * 128) + (1 * 64) + (1 * 32) + (0 * 16) + (0 * 8) + (0 * 4) + (1 * 2) + (0 * 1 ) = 64 + 32 + 2 = 98
- поскольку исходный бит знака был отрицательным, окончательное значение равно -98.
Небольшой тест
Вопрос 1
Преобразуйте 0100 1101 в десятичную форму.
Ответ
| Двоичное число | 1 | 1 | 1 | 1 | ||||
|---|---|---|---|---|---|---|---|---|
| * Значение цифры | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| = Результат (77) | 64 | 8 | 4 | 1 |
Ответ 77.
Вопрос 2
Преобразуйте 93 в 8-битное двоичное число без знака. Используйте оба метода, описанные выше.
Ответ
Используя метод 1:
Работая с остатками в обратном направлении, получаем 101 1101
Используя метод 2:
- Наибольшее значение двойки, возведенной в степень, которое меньше 93, равно 64.
- 93 >= 64? Да, поэтому бит со значением 64 равен 1. 93 — 64 = 29.
- 29 >= 32? Нет, поэтому бит со значением 32 равен 0.
- 29 >= 16? Да, поэтому бит со значением 16 равен 1. 29 — 16 = 13.
- 13 >= 8? Да, поэтому бит со значением 8 равен 1. 13 — 8 = 5.
- 5 >= 4? Да, поэтому бит со значением 4 равен 1. 5 — 4 = 1.
- 1 >= 2? Нет, поэтому бит со значением 2 равен 0.
- 1 >= 1? Да, поэтому бит со значением 1 равен 1.
Ответ: 0101 1101.
Вопрос 3
Преобразуйте -93 в 8-битное двоичное число со знаком (с использованием дополнительного кода).
Ответ
- Из предыдущего ответа мы уже знаем, что 93 – это 0101 1101
- Для дополнительного кода инвертируем биты: 1010 0010
- И прибавляем 1: 1010 0011
Вопрос 4
Преобразуйте 1010 0010 в десятичное число без знака.
Ответ
Работаем справа налево:
1010 0010 = (0 * 1) + (1 * 2) + (0 * 4) + (0 * 8) + (0 * 16) + (1 * 32) + (0 * 64) + (1 * 128) = 2 + 32 + 128 = 162
Ответ: 162.
Вопрос 5
Преобразуйте 1010 0010 в десятичное число со знаком (исходное число представлено в дополнительном коде).
Ответ
Поскольку нам сказано, что это число представлено в дополнительном коде, мы можем «отменить» дополнительный код, инвертировав биты и добавив 1.
- Сначала начнем с нашего двоичного числа: 1010 0010
- Инвертируем биты: 0101 1101
- Добавляем 1: 0101 1110
- Преобразуем в десятичную форму: 64 + 16 + 8 + 4 + 2 = 94
- Помним, что это дополнительный код, а исходный левый бит был отрицательным: -94
Ответ: -94
Вопрос 6
Напишите программу, которая просит пользователя ввести число от 0 до 255. Напечатайте это число как 8-битное двоичное число (в форме #### ####). Не используйте побитовые операторы. Не используйте .
Подсказка 1
Используйте метод 2. Предположим, что наибольшее значение двойки, возведенной в степень, равно 128.
Подсказка 2
Напишите функцию, чтобы проверить, больше ли введенное вами число, чем значение двойки, возведенной в некоторую степень. Если да, выведите ‘1’ и верните свое число за вычетом значения двойки, возведенной в степень.
Ответ
Перевод из восьмеричной системы в двоичную
Способ 1:
Каждый разряд восьмеричного числа будем делить на 2 и записывать остатки в обратном порядке, формируя группы по 3 разряда двоичного числа. Если в группе получилось меньше 3 разрядов, тогда дополняем нулями. Записываем все группы по порядку, отбрасываем ведущие нули, если имеются, и получаем двоичное число.
Возьмем число 438.
Делим последовательно 4 на 2 и получаем остатки 0,0,1. Записываем их в обратном порядке. Получаем 100.
Делим последовательно 3 на 2 и получаем остатки 1,1. Записываем их в обратном порядке и дополняем ведущими нулями до трех разрядов. Получаем 011.
Записываем вместе и получаем 1000112
Способ 2:
Используем таблицу триад:
| Цифра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| Триада | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
Каждую цифру исходного восьмеричного числа заменяется на соответствующие триады. Ведущие нули самой первой триады отбрасываются.
3518 = (011) (101) (001) = 0111010012 = 111010012
4.12. Как компьютер выполняет арифметические действия над целыми числами?
Сложение и вычитание
| В большинстве компьютеров операция вычитания не используется. Вместо нее производится сложение уменьшаемого с обратным или дополнительным кодом вычитаемого. Это позволяет существенно упростить конструкцию АЛУ. |
При сложении обратных кодов чисел А и В имеют место четыре основных и два
особых случая:
1. А и В положительные. При суммировании складываются все разряды,
включая разряд знака. Так как знаковые разряды положительных слагаемых равны
нулю, разряд знака суммы тоже равен нулю. Например:

Получен правильный результат.
2. А положительное, B отрицательное и по абсолютной величине больше, чем
А. Например:
Получен правильный результат в обратном коде. При переводе в прямой код биты
цифровой части результата инвертируются: 1 0000111 = –710.
3. А положительное, B отрицательное и по абсолютной величине меньше, чем
А. Например:

Компьютер исправляет полученный первоначально неправильный результат (6
вместо 7) переносом единицы из знакового разряда в младший разряд суммы.
4. А и В отрицательные. Например:

Полученный первоначально неправильный результат (обратный код числа
–1110 вместо обратного кода числа –1010) компьютер
исправляет переносом единицы из знакового разряда в младший разряд суммы.
При переводе результата в прямой код биты цифровой части числа инвертируются:
1 0001010 = –1010.
При сложении может возникнуть ситуация, когда старшие разряды результата
операции не помещаются в отведенной для него области памяти. Такая ситуация
называется переполнением разрядной сетки формата числа. Для
обнаружения переполнения и оповещения о возникшей ошибке в компьютере
используются специальные средства. Ниже приведены два возможных случая
переполнения.
5. А и В положительные, сумма А+В больше, либо равна 2n–1,
где n – количество разрядов формата чисел (для однобайтового формата n=8,
2n–1 = 27 = 128). Например:
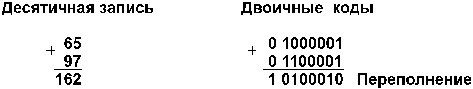
Семи разрядов цифровой части числового формата недостаточно для
размещения восьмиразрядной суммы (16210 = 101000102),
поэтому старший разряд суммы оказывается в знаковом разряде. Это вызывает
несовпадение знака суммы и знаков слагаемых, что является
свидетельством переполнения разрядной сетки.
6. А и В отрицательные, сумма абсолютных величин А и В больше, либо равна
2n–1. Например:

Здесь знак суммы тоже не совпадает со знаками слагаемых, что
свидетельствует о переполнении разрядной сетки.
Все эти случаи имеют место и при сложении дополнительных кодов чисел:
1. А и В положительные. Здесь нет отличий от случая 1, рассмотренного
для обратного кода.
2. А положительное, B отрицательное и по абсолютной величине больше, чем
А. Например:

Получен правильный результат в дополнительном коде. При переводе в прямой код
биты цифровой части результата инвертируются и к младшему разряду прибавляется
единица: 1 0000110 + 1 = 1 0000111 = –710.
3. А положительное, B отрицательное и по абсолютной величине меньше, чем
А. Например:

Получен правильный результат. Единицу переноса из знакового разряда компьютер
отбрасывает.
4. А и В отрицательные. Например:

Получен правильный результат в дополнительном коде. Единицу переноса
из знакового разряда компьютер отбрасывает.
Случаи переполнения для дополнительных кодов рассматриваются по
аналогии со случаями 5 и 6 для обратных кодов.
Сравнение рассмотренных форм кодирования целых чисел со знаком показывает:
-
на преобразование отрицательного числа в обратный код компьютер
затрачивает меньше времени, чем на преобразование в дополнительный код,
так как последнее состоит из двух шагов — образования обратного кода и
прибавления единицы к его младшему разряду; -
время выполнения сложения для дополнительных кодов чисел меньше, чем
для их обратных кодов, потому что в таком сложении нет переноса единицы из
знакового разряда в младший разряд результата.
Умножение и деление
Во многих компьютерах умножение производится как последовательность
сложений и сдвигов. Для этого в АЛУ имеется регистр, называемый
накапливающим сумматором, который до начала выполнения операции
содержит число ноль. В процессе выполнения операции в нем поочередно
размещаются множимое и результаты промежуточных сложений, а по
завершении операции — окончательный результат.
Другой регистр АЛУ, участвующий в выполнении этой операции, вначале
содержит множитель. Затем по мере выполнения сложений содержащееся в нем
число уменьшается, пока не достигнет нулевого значения.
Для иллюстрации умножим 1100112 на 1011012.

Деление для компьютера является трудной операцией. Обычно оно
реализуется путем многократного прибавления к делимому дополнительного кода
делителя.
4.3. Какие системы счисления используют специалисты для общения с компьютером?
Кроме десятичной широко используются системы с основанием, являющимся
целой степенью числа 2, а именно:
- двоичная (используются цифры 0, 1);
- восьмеричная (используются цифры 0, 1, …, 7);
-
шестнадцатеричная (для первых целых чисел от нуля до девяти
используются цифры 0, 1, …, 9, а для следующих чисел — от десяти до
пятнадцати – в качестве цифр используются символы A, B, C, D, E, F).
Полезно запомнить запись в этих системах счисления первых двух десятков целых
чисел:
|
|
Из всех систем счисления особенно проста и поэтому интересна для
технической реализации в компьютерах двоичная система счисления.
Перевод целого двоичного числа в шестнадцатеричную систему счисления
Пример 1: перевести 1011101 из двоичной системы в шестнадцатеричную.
Как было сказано выше, необходимо сначала перевести число в десятичное, а полученный ответ в шестнадцатеричную. Решение будет выглядеть следующим образом:
Для перевода двоичного числа 1011101 в десятичную систему, воспользуемся формулой:
A2 = an-1 ∙ 2n-1 + an-2 ∙ 2n-2 + ∙∙∙ + a ∙ 2, отсюда:
10111012=1 ∙ 26 + 0 ∙ 25 + 1 ∙ 24 + 1 ∙ 23 + 1 ∙ 22 + 0 ∙ 21 + 1 ∙ 2 = 1 ∙ 64 + 0 ∙ 32 + 1 ∙ 16 + 1 ∙ 8 + 1 ∙ 4 + 0 ∙ 2 + 1 ∙ 1 = 64 + 0 + 16 + 8 + 4 + 0 + 1 = 9310
Таким образом:
10111012 = 9310
Полученное число 93 переведем из десятичной системы счисления в шестнадцатеричную. Для этого, осуществим последовательное деление на 16, до тех пор пока остаток не будет меньше чем 16.
Полученные остатки записываем в обратном порядке, таким образом:
9310=5D16
Ответ: 10111012 = 5D16.
Способ №1.
Допустим, требуется перевести число 637 десятичной системы в двоичную систему.
Делается это следующим образом: отыскивается максимальная степень двойки, чтобы два в этой степени было меньше или равно исходному числу.
В нашем случае это 9, т.к. 29=512, а 210=1024, что больше нашего начального числа. Таким образом, мы получили число разрядов результата. Оно равно 9+1=10. Значит, результат будет иметь вид 1ххххххххх, где вместо х может стоять 1 или 0.
Найдем вторую цифру результата. Возведем двойку в степень 9 и вычтем из исходного числа: 637-29=125. Затем сравниваем с числом 28=256. Так как 125 меньше 256, то девятый разряд будет 0, т.е. результат уже примет вид 10хххххххх.
27=128 > 125, значит и восьмой разряд будет нулём.
26=64, то седьмой разряд равен 1. 125-64=61 Таким образом, мы получили четыре старших разряда и число примет вид 10011ххххх.
25=32 и видим, что 32 < 61, значит шестой разряд равен 1 (результат 100111хххх), остаток 61-32=29.
24=16 < 29 — пятый разряд 1 => 1001111ххх. Остаток 29-16=13.
23=8 < 13 => 10011111хх. 13-8=5
22=4 < 5 => 10011111хх, остаток 5-4=1.
21=2 > 1 => 100111110х, остаток 2-1=1.
2=1 => 1001111101.
Это и будет конечный результат.
Восьмеричная и шестнадцатеричная системы счисления
Эти системы счисления относятся к двоично-кодированным, в которых основание системы счисления
представляет собой целую степень двойки: —
для восьмеричной и — для шестнадцатеричной.
В восьмеричной системе счисления(s = 8) используются 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7.
Прежде чем заняться переводом из любой системы счисления в восьмеричную, нужно внимательно изучить пример записи числа в восьмеричной системе:
В шестнадцатеричной системе счисления (s = 16) используются 16 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Пример записи числа в шестнадцатеричной системе:
Широкое применение восьмеричной и шестнадцатеричной систем счисления обусловлено двумя факторами.
Во-первых, эти системы позволяют заменить запись двоичного числа более компактным представлением
(запись числа в восьмеричной и шестнадцатеричной системах будет соответственно в 3 и 4 раза короче двоичной записи этого числа).
Во-вторых, взаимное преобразование чисел между двоичной системой с одной стороны и восьмеричной и шестнадцатиречной — с другой
осуществляется сравнительно просто. Действительно, поскольку для восьмеричного числа каждый разряд представляется
группой из трёх двоичных разрядов (триад), а для шестнадцатеричного — группой из четырёх двоичных разрядов (тетрад),
то для преобразования двоичного числа достаточно объединить его цифры в группы по 3 или 4 разряда соответственно, продвигаясь от
разделительной запятой вправо и влево. При этом, в случае необходимости, добавляют нули слева от целой части
и/или справа от дробной части и каждую такую группу — триаду или тетраду — заменяют эвивалентной восьмеричной или
шестнадцатеричной цифрой (см. таблицу).
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат,
то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления
в другие системы.
Для обратного перевода каждая OCT или HEX цифра заменяется соответственно триадой или тетрадой
двоичных цифр, причём незначащие нули слева и справа отбрасываются.
Для рассмотренных ранее примеров это выглядит следующим образом:
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат,
то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления
в другие системы.
4.2. Как порождаются целые числа в позиционных системах счисления?
В каждой системе счисления цифры упорядочены в соответствии с их значениями:
1 больше 0, 2 больше 1 и т.д.
|
Продвижением цифры называют замену её следующей по величине. |
Продвинуть цифру 1 значит заменить её на 2, продвинуть цифру 2 значит
заменить её на 3 и т.д. Продвижение старшей цифры (например, цифры 9 в
десятичной системе) означает замену её на 0. В двоичной системе,
использующей только две цифры – 0 и 1, продвижение 0 означает замену его на 1, а
продвижение 1 – замену её на 0.
Целые числа в любой системе счисления порождаются с помощью Правила
счета :
| Для образования целого числа, следующего за любым данным целым числом, нужно продвинуть самую правую цифру числа; если какая-либо цифра после продвижения стала нулем, то нужно продвинуть цифру, стоящую слева от неё. |
Применяя это правило, запишем первые десять целых чисел
- в двоичной системе: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001;
- в троичной системе: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100;
- в пятеричной системе: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14;
- восьмеричной системе: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11.
Десятичное в двоичное преобразование в C++
Чтобы преобразовать десятичное число в двоичное число в программировании на C++ , вы должны попросить пользователя ввести десятичное число, чтобы преобразовать его в двоичное число, чтобы отобразить эквивалентное значение в двоичном формате, как показано здесь в следующей программе.
Программный код C++ Преобразование десятичного числа в двоичный
После программы на C++ попросите пользователя ввести любое число в десятичном формате, чтобы преобразовать его в двоичный, а затем отобразить результат на экране:
Когда вышеупомянутая программа C++ компилируется и выполняется, она даст следующий результат:
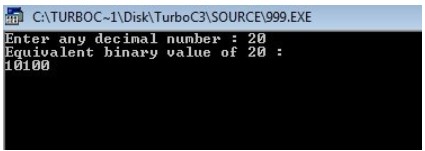
Как создать программу на C, которая преобразует любое заданное число (в десятичном числе) пользователем во время выполнения в его эквивалентное значение в двоичном числе. Наконец, мы также создали программу, которая использует пользовательскую функцию для преобразования десятичного числа в двоичное.
Преобразовать десятичное в двоичное в Python
Чтобы преобразовать десятичное число в двоичное в Python, вы должны попросить пользователя ввести число в десятичной системе счисления, чтобы преобразовать это число в двоичную систему счисления, как показано в программе, приведенной ниже.
Программный код Python для преобразования десятичного числа в двоичное
Следующая программа на Python просит пользователя ввести десятичное число, чтобы преобразовать его в двоичное число:
Вот пример запуска вышеупомянутой программы Python, чтобы продемонстрировать, как преобразовать десятичное число в двоичное в Python:
Теперь введите любое число в десятичной системе счисления, скажем, 50, а затем нажмите клавишу ввода, чтобы проверить, каково будет значение данного числа, скажем, 50 в двоичном формате:
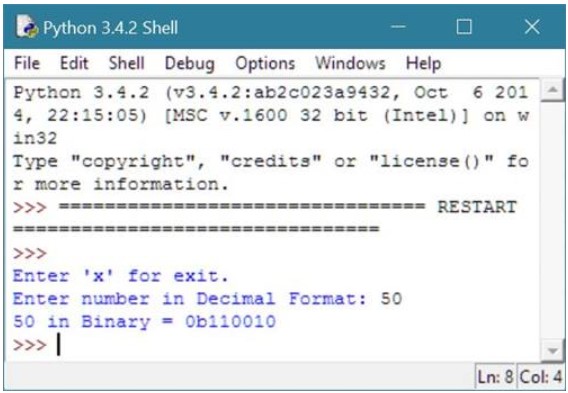
Ниже та же программа на оболочке Python:
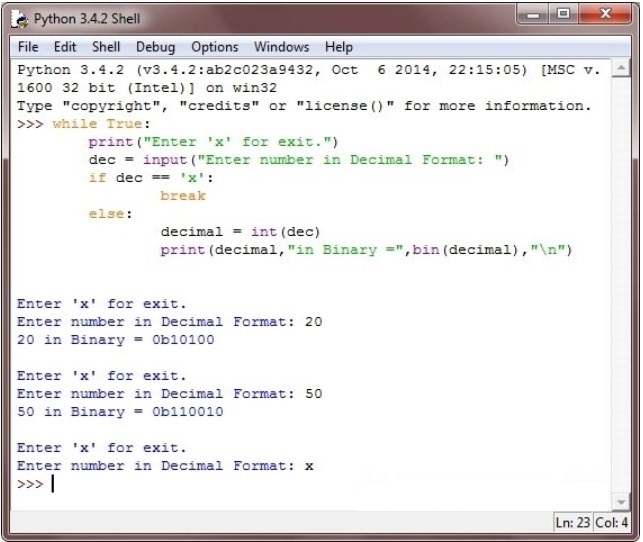
Интересные записи:
Преобразовать десятичную в двоичную
Чтобы преобразовать десятичное число в двоичное в Java Programming, вам нужно попросить пользователя ввести любое число в формате десятичного числа, чтобы преобразовать его в формат двоичного числа для отображения эквивалентного значения в двоичной системе счисления, как показано в следующей программе.
Программный код Java для преобразования десятичного числа в двоичное
После Java-программы попросите пользователя ввести любое десятичное число, чтобы преобразовать его в двоичный, а затем отобразить результат на экране:
Когда вышеуказанная Java-программа компилируется и выполняется, она выдаст следующий вывод:
Перевод любого дробного числа из одной системы в другую
Пример 3: перевести 231.20 из четверичной в семеричную систему счисления.
Общий смысл алгоритма перевода дробного числа, аналогичен алгоритму перевода целого, т.е. вначале переводим в десятичную, а затем в семеричную:
1. Для перевода числа 231.20 в десятичную систему воспользуемся формулой:
An = an-1 ∙ qn-1 + an-2 ∙ qn-2 + ∙∙∙ + a ∙ q + a-1 ∙ q-1 + ∙∙∙ + a-m ∙ q-m
Отсюда:
231.204=2 ∙ 42 + 3 ∙ 41 + 1 ∙ 4 + 2 ∙ 4-1 + 0 ∙ 4-2 = 2 ∙ 16 + 3 ∙ 4 + 1 ∙ 1 + 2 ∙ 0.25 + 0 ∙ 0.0625 = 32 + 12 + 1 + 0.5 + 0 = 45.510
Таким образом:
231.204 = 45.510
2. Полученное число 45.5 переведем из десятичной системы счисления в семеричную. Т.к. полученное число содержит дробную часть, нам потребуется перевести вначале целую часть, а затем дробную. Таким образом необходимо:
- Перевести 45 в семеричную систему;
- Перевести 0.5 в семеричную систему;
2.1 Для того, чтобы перевести число 45 из десятичной системы счисления в 7-ую, необходимо осуществить последовательное деление на 7, до тех пор пока остаток не будет меньше чем 7.
Полученные остатки записываем в обратном порядке, таким образом:
4510=637
2.2 Для перевода десятичной дроби 0.5 в 7-ую систему, необходимо выполнить последовательное умножение дроби на 7, до тех пор, пока дробная часть не станет равной 0 или пока не будет достигнута заданная точность вычисления. Получаем:
0.5 ∙ 7 = 3.5 (3) 0.5 ∙ 7 = 3.5 (3) 0.5 ∙ 7 = 3.5 (3) 0.5 ∙ 7 = 3.5 (3) 0.5 ∙ 7 = 3.5 (3) 0.5 ∙ 7 = 3.5 (3) 0.5 ∙ 7 = 3.5 (3) 0.5 ∙ 7 = 3.5 (3) 0.5 ∙ 7 = 3.5 (3) 0.5 ∙ 7 = 3.5 (3) 0.5 ∙ 7 = 3.5 (3)
Ответом станет прямая последовательность целых частей произведения. Т.е.
0.510=0.333333333337
2.3. Осталось соединить переведенные части, таким образом:
45.510=63.333333333337
Ответ: 231.204 = 63.333333333337.
Двоичная система счисления
Основанием системы счисления служит число 2 (s = 2) и для записи чисел используются только
две цифры: 0 и 1. Чтобы представить любой разряд двоичного числа, достаточно иметь физический элемент
с двумя чётко различными устойчивыми состояниями, одно из которых изображает 1, а другое 0.
Прежде чем заняться переводом из любой системы счисления в двоичную, нужно внимательно изучить пример записи числа в двоичной системе счисления:
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат,
то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления
в другие системы.
Преобразование числа из двоичной системы счисления в десятичную
В следующих примерах предполагается, что мы имеем дело с целыми числами без знака.
Рассмотрим 8-битное (1 байт) двоичное число 0101 1110. Двоичное 0101 1110 означает (0 * 128) + (1 * 64) + (0 * 32) + (1 * 16) + (1 * 8) + (1 * 4) + (1 * 2) + (0 * 1). Если просуммировать все эти части, мы получим десятичное число 64 + 16 + 8 + 4 + 2 = 94.
Ниже показан тот же процесс в формате таблицы. Мы умножаем каждую двоичную цифру на ее числовое значение (определяемое ее позицией). Суммирование всех этих значений дает нам итоговый результат.
Преобразование 0101 1110 в десятичную форму:
| Двоичное число | 1 | 1 | 1 | 1 | 1 | |||
|---|---|---|---|---|---|---|---|---|
| * Значение цифры | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| = Результат (94) | 64 | 16 | 8 | 4 | 2 |
Преобразуем 1001 0111 в десятичную форму:
| Двоичное число | 1 | 1 | 1 | 1 | 1 | |||
|---|---|---|---|---|---|---|---|---|
| * Значение цифры | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| = Результат (151) | 128 | 16 | 4 | 2 | 1 |
1001 0111 в двоичном формате = 151 в десятичном формате.
Этот способ можно легко расширить до 16- или 32-битных двоичных чисел, просто добавив дополнительные столбцы
Обратите внимание, что проще всего начать с правого конца и двигаться влево, умножая значение цифры на 2 по мере продвижения
Таблица перевода десятичных чисел от 0 до 20 в двоичную систему счисления.
|
десятичное число |
двоичное число |
десятичное число |
двоичное число |
|
0000 |
11 |
1011 |
|
|
1 |
0001 |
12 |
1100 |
|
2 |
0010 |
13 |
1101 |
|
3 |
0011 |
14 |
1110 |
|
4 |
0100 |
15 |
1111 |
|
5 |
0101 |
16 |
10000 |
|
6 |
0110 |
17 |
10001 |
|
7 |
0111 |
18 |
10010 |
|
8 |
1000 |
19 |
10011 |
|
9 |
1001 |
20 |
10100 |
|
10 |
1010 |
и т.д. |
Однако таблица получится огромной, если записать туда все числа. Искать среди них нужное число будет уже сложнее. Гораздо проще запомнить несколько алгоритмов перевода чисел из одной позиционной системы счисления в другую.
Как сделать перевод из одной системы счисления в другую? В информатике существует несколько простых способов перевода десятичных чисел в двоичные числа. Рассмотрим два из них.
Перевод чисел из десятичной системы счисления в другую систему счисления
Для перевода чисел из десятичной системы счисления в другую систему счисления нужно переводить отдельно целую часть числа и дробную часть числа.
Целую часть числа переводится из десятичной СС в другую систему счисления — последовательным делением целой части числа на основание системы счисления (для двоичной СС — на 2, для 8-ичной СС — на 8, для 16-ичной — на 16 и т.д.) до получения целого остатка, меньше, чем основание СС.
Пример 4. Переведем число 159 из десятичной СС в двоичную СС:
| 159 | 2 | ||||||
| 158 | 79 | 2 | |||||
| 1 | 78 | 39 | 2 | ||||
| 1 | 38 | 19 | 2 | ||||
| 1 | 18 | 9 | 2 | ||||
| 1 | 8 | 4 | 2 | ||||
| 1 | 4 | 2 | 2 | ||||
| 2 | 1 |
Рис. 1
Как видно из Рис. 1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111. Следовательно можно записать:
Пример 5. Переведем число 615 из десятичной СС в восьмеричную СС.
| 615 | 8 | ||
| 608 | 76 | 8 | |
| 7 | 72 | 9 | 8 |
| 4 | 8 | 1 | |
| 1 |
Рис. 2
При приведении числа из десятичной СС в восьмеричную СС, нужно последовательно делить число на 8, пока не получится целый остаток меньшее, чем 8. В результате построив число из остатков деления (справа налево) получим число в восьмеричной СС: 1147(см. Рис. 2). Следовательно можно записать:
Пример 6. Переведем число 19673 из десятичной системы счисления в шестнадцатеричную СС.
| 19673 | 16 | ||
| 19664 | 1229 | 16 | |
| 9 | 1216 | 76 | 16 |
| 13 | 64 | 4 | |
| 12 |
Рис. 3
Как видно из рисунка Рис.3, последовательным делением числа 19673 на 16 получили остатки 4, 12, 13, 9. В шестнадцатеричной системе счисления числе 12 соответствует С, числе 13 — D. Следовательно наше шестнадцатеричное число — это 4CD9.
Далее рассмотрим перевод правильных десятичных дробей в двоичную СС, в восьмеричную СС, в шестнадцатеричную СС и т.д.
Для перевода правильных десятичных дробей (вещественное число с нулевой целой частью) в систему счисления с основанием s необходимо данное число последовательно умножить на s до тех пор, пока в дробной части не получится чистый нуль, или же не получим требуемое количество разрядов. Если при умножении получится число с целой частью, отличное от нуля, то эту целую часть не учитывать (они последовательно зачисливаются в результат).
Рассмотрим вышеизложенное на примерах.
Пример 7. Переведем число 0.214 из десятичной системы счисления в двоичную СС.
| 0.214 | ||
| x | 2 | |
| 0.428 | ||
| x | 2 | |
| 0.856 | ||
| x | 2 | |
| 1 | 0.712 | |
| x | 2 | |
| 1 | 0.424 | |
| x | 2 | |
| 0.848 | ||
| x | 2 | |
| 1 | 0.696 | |
| x | 2 | |
| 1 | 0.392 |
Рис. 4
Как видно из Рис.4, число 0.214 последовательно умножается на 2. Если в результате умножения получится число с целой частью, отличное от нуля, то целая часть записывается отдельно (слева от числа), а число записывается с нулевой целой частью. Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0.0011011.
Следовательно можно записать:
Пример 8. Переведем число 0.125 из десятичной системы счисления в двоичную СС.
| 0.125 | ||
| x | 2 | |
| 0.25 | ||
| x | 2 | |
| 0.5 | ||
| x | 2 | |
| 1 | 0.0 |
Рис. 5
Для приведения числа 0.125 из десятичной СС в двоичную, данное число последовательно умножается на 2. В третьем этапе получилось 0. Следовательно, получился следующий результат:
Пример 9. Переведем число 0.214 из десятичной системы счисления в шестнадцатеричную СС.
| 0.214 | ||
| x | 16 | |
| 3 | 0.424 | |
| x | 16 | |
| 6 | 0.784 | |
| x | 16 | |
| 12 | 0.544 | |
| x | 16 | |
| 8 | 0.704 | |
| x | 16 | |
| 11 | 0.264 | |
| x | 16 | |
| 4 | 0.224 |
Рис. 6
Следуя примерам 4 и 5 получаем числа 3, 6, 12, 8, 11, 4. Но в шестнадцатеричной СС числам 12 и 11 соответствуют числа C и B. Следовательно имеем:
Пример 10. Переведем число 0.512 из десятичной системы счисления в восьмеричную СС.
| 0.512 | ||
| x | 8 | |
| 4 | 0.096 | |
| x | 8 | |
| 0.768 | ||
| x | 8 | |
| 6 | 0.144 | |
| x | 8 | |
| 1 | 0.152 | |
| x | 8 | |
| 1 | 0.216 | |
| x | 8 | |
| 1 | 0.728 |
Рис. 7
Получили:
Пример 11. Переведем число 159.125 из десятичной системы счисления в двоичную СС. Для этого переведем отдельно целую часть числа (Пример 4) и дробную часть числа (Пример 8). Далее объединяя эти результаты получим:
Пример 12. Переведем число 19673.214 из десятичной системы счисления в шестнадцатеричную СС. Для этого переведем отдельно целую часть числа (Пример 6) и дробную часть числа (Пример 9). Далее объединяя эти результаты получим:
4.4. Почему люди пользуются десятичной системой, а компьютеры — двоичной?
Люди предпочитают десятичную систему, вероятно, потому, что с древних времен
считали по пальцам, а пальцев у людей по десять на руках и ногах. Не всегда и не
везде люди пользуются десятичной системой счисления. В Китае, например, долгое
время пользовались пятеричной системой счисления.
А компьютеры используют двоичную систему потому, что она имеет ряд
преимуществ перед другими системами:
- для ее реализации нужны технические устройства с двумя устойчивыми
состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а
не, например, с десятью, — как в десятичной; - представление информации посредством только двух состояний надежно
и помехоустойчиво; - возможно применение аппарата булевой алгебры для выполнения
логических преобразований информации; - двоичная арифметика намного проще десятичной.
Недостаток двоичной системы — быстрый рост числа разрядов, необходимых
для записи чисел.