Закон Джоуля-Ленца
На примере многих бытовых приборов понятно, что если через участок цепи проходит электроток и при этом не совершается какая-либо работа, то происходит нагревание проводника. Иногда оно идет на пользу — например, в лампе накаливания или в аппарате дуговой сварки. Но в других случаях тепловой эффект нежелателен — например, перегрев электрической проводки в здании может вызвать пожар. Поэтому в наших интересах управлять таким эффектом, и правило Джоуля-Ленца определяет, от чего зависит тепловое действие тока.
Правило было сформулировано в результате опытов двух ученых — англичанина Джеймса Прескотта Джоуля и российского физика Эмилия Христиановича Ленца. Поскольку ученые работали независимо друг от друга, новый закон назвали двойным именем.
|
Закон Джоуля-Ленца кратко: нагревание проводника или полупроводника прямо пропорционально его сопротивлению, времени действия тока и квадрату силы тока. |
Поскольку сопротивление проводника определяют такие характеристики, как его длина, площадь и проводимость, верны следующие утверждения:
-
количество теплоты в проводнике снижается при увеличении площади его сечения;
-
тепловой эффект снижается при уменьшении длины проводника.
Это легко проиллюстрировать, подключив к источнику питания две лампы с разным сопротивлением вначале последовательно, а после — параллельно. При последовательном подключении лампа с большим сопротивлением будет светить ярче, а при параллельном — наоборот.
Гидравлическая аналогия
Чтобы легче усвоить законы электрических цепей, можно представить себе аналогию с гидравлической системой, в которой соединение насоса и трубопроводов образует замкнутую систему. Для этого нужны следующие соответствия:
- Источник питания – насос;
- Проводники – трубы;
- Электроток – движение воды.
Без особых усилий становится понятнее, что чем меньше диаметр труб, тем медленнее по ним движется вода. Чем мощнее насос, тем большее количество воды он способен перекачать. При одинаковой мощности насоса уменьшение диаметра труб приведет к снижению потока воды.
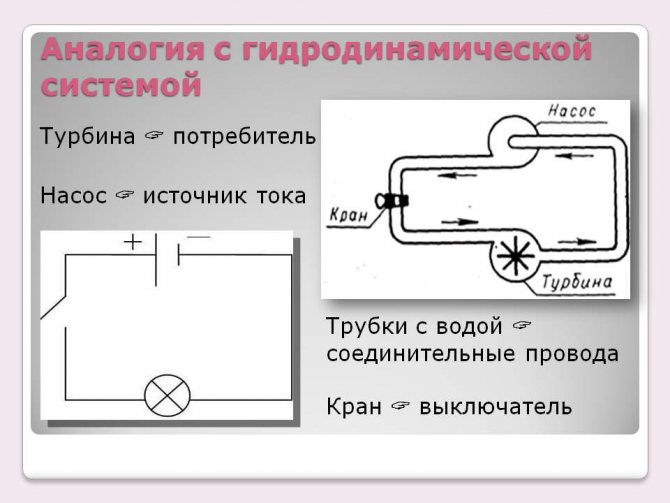
Гидравлическая аналогия
Значения других единиц, равные введённым выше
открыть
свернуть
Международная система (СИ)
|
джоуль в секунду → мегаватт (МВт) |
|
|
джоуль в секунду → киловатт (кВт) |
|
джоуль в секунду → ватт (Вт) |
|
|
джоуль в секунду → вольт-ампер (В-А) |
Единицы:
мегаватт
(МВт)
/
киловатт
(кВт)
/
ватт
(Вт)
/
вольт-ампер
(В-А)
открыть
свернуть
СГС и внесистемные единицы
| джоуль в секунду → гигакалорий в секунду | |
| джоуль в секунду → килокалорий в секунду | |
| джоуль в секунду → калорий в секунду | |
| джоуль в секунду → гигакалорий в минуту | |
| джоуль в секунду → килокалорий в минуту | |
| джоуль в секунду → калорий в минуту | |
| джоуль в секунду → гигакалорий в час | |
| джоуль в секунду → килокалорий в час | |
| джоуль в секунду → калорий в час | |
|
джоуль в секунду → котловая лошадиная сила (hp(S)) |
|
джоуль в секунду → электрическая лошадиная сила (hp(E)) |
|
| джоуль в секунду → гидравлическая лошадиная сила | |
|
джоуль в секунду → механическая лошадиная сила (hp(I)) |
|
|
джоуль в секунду → метрическая лошадиная сила (hp(M)) |
|
|
джоуль в секунду → килограмм-сила метр в секунду (кгс*м/с) |
|
| джоуль в секунду → джоуль в секунду | |
| джоуль в секунду → джоуль в минуту | |
| джоуль в секунду → джоуль в час | |
| джоуль в секунду → эрг в секунду | |
|
джоуль в секунду → метрическая тонна охлаждения (RT) |
|
|
джоуль в секунду → фригория в час (fg/h) |
Единицы:
гигакалорий в секунду
/
килокалорий в секунду
/
калорий в секунду
/
гигакалорий в минуту
/
килокалорий в минуту
/
калорий в минуту
/
гигакалорий в час
/
килокалорий в час
/
калорий в час
/
котловая лошадиная сила
(hp(S))
/
электрическая лошадиная сила
(hp(E))
/
гидравлическая лошадиная сила
/
механическая лошадиная сила
(hp(I))
/
метрическая лошадиная сила
(hp(M))
/
килограмм-сила метр в секунду
(кгс*м/с)
/
джоуль в секунду
/
джоуль в минуту
/
джоуль в час
/
эрг в секунду
/
метрическая тонна охлаждения
(RT)
/
фригория в час
(fg/h)
открыть
свернуть
Британские и американские единицы
|
джоуль в секунду → американская тонна охлаждения (USRT) |
|
|
джоуль в секунду → британская термальная единица в секунду (BTU/s) |
|
джоуль в секунду → британская термальная единица в минуту (BTU/min) |
|
|
джоуль в секунду → британская термальная единица в час (BTU/hr) |
|
|
джоуль в секунду → фут фунт-сила в секунду (ft*lbf/s) |
Единицы:
американская тонна охлаждения
(USRT)
/
британская термальная единица в секунду
(BTU/s)
/
британская термальная единица в минуту
(BTU/min)
/
британская термальная единица в час
(BTU/hr)
/
фут фунт-сила в секунду
(ft*lbf/s)
открыть
свернуть
Естественнные единицы
В физике естественные единицы измерения базируются только на фундаментальных физических константах. Определение этих единиц никак не связано ни с какими историческими человеческими построениями, только с фундаментальными законами природы.
|
джоуль в секунду → планковская мощность (L²MT⁻³) |
Единицы:
планковская мощность
(L²MT⁻³)
История программ количественного смягчения
В США
По данным историков экономики, первый выкуп ценных бумаг регулятором был осуществлен в США еще в 1932 году, его объем составил $1 млрд. Но сам термин Quantitative easing появился в 2009 году, когда американский Федрезерв начал первый этап программы под таким названием.
Количественное смягчение в США проходило в три этапа:
- в рамках QE1, начатой в конце 2008 года, было эмитировано около $1,5 трлн.;
- QE2 началась в 2010 году и за полгода достигла показателя $600 млрд;
- QE3 стартовала в 2012 году и началась с объема $40 млрд в месяц, который затем был увеличен до $85 млрд. Закончилась третья программа в конце октября 2014 года, когда ее общий объем достиг $1,6 трлн.
Пусть за счет увеличения госдолга, экономика США избавилась от последствий мирового финансового кризиса, а ВВП вырос с $14,72 трлн. долларов в 2008 до $16,77 трлн. в 2013 году.
В Японии
Количественное смягчение в Японии в нынешнем веке началось даже раньше, чем в Штатах, а именно в марте 2001, и длилось с перерывами более десяти лет. За первые четыре года Банк Японии в семь раз (с 5 до 35 триллионов иен, или около $300 млрд) увеличил текущий баланс коммерческих банковских организаций и в три раза – количество покупаемых ежемесячно облигаций правительства страны.
В 2013 году Банк Японии анонсировал переход с количественного на количественное и качественное смягчение. Новая монетарная политика состоит в выкупе гособлигаций с более длительным сроком обращения и одновременным увеличением объема выкупаемых регулятором активов. В 2016 году общий объем QE достиг почти $670 млрд. Согласно прогнозу Центробанка, в 2017 ему наконец удастся добиться целевого уровня инфляции на уровне 2%. В итоге результаты не отрицательные, но тем не менее незначительные.
В Еврозоне
В странах, которые входят в зону евро, количественное смягчение ЕЦБ стартовало в марте 2015 года и продолжается до сих пор. Активы выкупаются на сумму €80 млрд в месяц, общий объем программы QE к марту 2017 года приблизился к €1,7 трлн.
Европейский регулятор выкупает ценные бумаги, доходность которых превышает показатель по его депозитам в -0,4% годовых.
В феврале 2017 инфляция в еврозоне достигла 0,38%, при этом показатель с начала года остался отрицательным, составив -0,46%. После двух лет со времени запуска программы нельзя однозначно сказать, что quantitative easing внесла оживление в европейскую экономику — хотя ряд европейских индексов почувствовал себя лучше, дав в 2016 году доходность около 10% годовых.
В Еврозоне QE включает в себя, по большому счету, не только сам ежемесячный выкуп бумаг, но и так называемые программы TLTRO (Targeted Long-Term Repo Operation, целевое долгосрочное кредитование), которые предоставляют возможность банкам привлекать фактически «халявные» деньги для дальнейшего кредитования бизнеса. При этом расходовать средства необходимо именно на кредитование, а не на покупку других активов — программа разбита на части и второй транш банки получают в зависимости от итогов по первому.
Первая программа стартовала осенью 2014 года. В рамках последнего (четвертого) раунда программы TLTRO-II, запущенной в июне 2016 года, Европейский центральный банк выдал различным финансовым компаниям кредиты более чем на 230 млрд. евро. Эмиссия евро, таким образом, началась по окончанию QE3 в США и привела к девальвации евро к доллару примерно на 20%, считая с 2014 года.
Возможно ли QE в России?
По словам главы ЦБ РФ г-жи Набиуллиной и ее первого заместителя Ксении Юдаевой, никакое количественное смягчение в России в настоящее время невозможно. Руководители Банка России объясняют это слишком малым объемом рынка госдолга РФ по сравнению со странами Запада. К тому же эти страны, внедряя QE, преследуют цели уменьшения безработицы и преодоления дефляции, а последнее для России вообще не актуально – ключевая ставка еще совсем недавно находилась на уровне 10%, что вписывается в тенденцию более высоких ставок у развивающихся стран. Подробнее об этом можно прочитать в статье о керри-трейд.
Удельная теплоемкость вещества
Это физическая величина, выражающая количество тепла, необходимое веществу на единицу массы для повышения температуры на одну единицу.
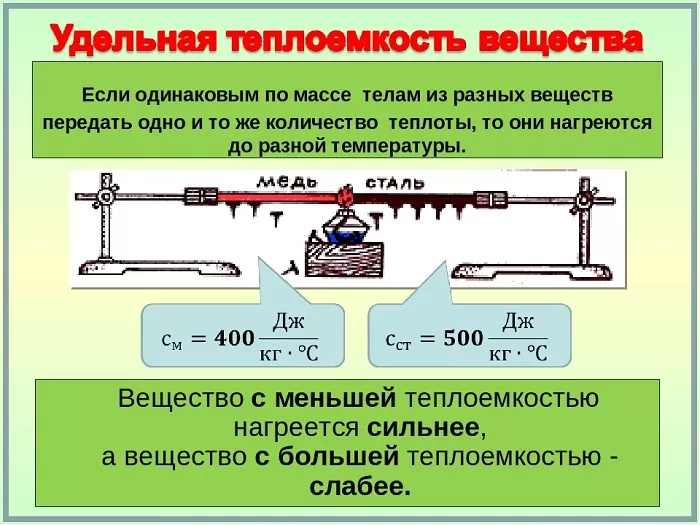
Таким образом, удельная теплоёмкость является свойством вещества, поскольку его значение является репрезентативным для каждого вещества, каждое из которых, в свою очередь, имеет различные значения в зависимости от того, в каком состоянии оно находится (жидкое, твердое или газообразное).
Удельная теплоёмкость обозначается маленькой буквой c и измеряется в Дж/кг∗°С, представляет собой коэффициент повышения температуры в одной единице всей системы или всей массы вещества.
Кроме того, удельная теплоёмкость меняется в зависимости от физического состояния вещества, особенно в случае твердых частиц и газов, поскольку его молекулярная структура влияет на теплопередачу в системе частиц. То же самое относится и к условиям атмосферного давления: чем выше давление, тем ниже удельное тепло.
Основной состав удельной теплоты вещества должен быть с = С/m, т. е. удельная теплота равна соотношению калорийности и массы.
Однако когда это применяется к данному изменению температуры, говорят о средней удельной теплоемкости, которая рассчитывается на основе следующей формулы:
где:
Q — передача тепловой энергии между системой и средой (Дж);
m — масса системы (кг);
Δt или (t2 — t1) — повышение температуры, которой она подвергается (°C).
Формула для нахождения количества теплоты Q:
Q = c∗m(t2— t1) Чем выше удельная теплоёмкость вещества, тем больше тепловой энергии потребуется, чтобы его температура повысилась. Например, для нагрева воды (своды = 4200 Дж/кг∗°С) потребуется больше тепловой энергии, чем для нагрева свинца (ссвинца = 140 Дж/кг∗°С).
Уравнение теплового баланса:
Q отданное + Q полученное = 0.
Ниже представлена таблица значений удельной теплоёмкости некоторых веществ:

Нахождение постоянной Больцмана через формулу броуновского движения
Для второго способа вычисления нам также потребуется провести эксперимент. Для него нужно взять небольшое зеркало и подвесить в воздухе с помощью упругой нитки. Допустим, что система зеркало-воздух находится в стабильном состоянии (статическом равновесии). Молекулы воздуха ударяют в зеркало, которое, по сути, ведет себя как броуновская частица. Однако с учетом его подвешенного состояния мы можем наблюдать вращательные колебания вокруг определенной оси, совпадающей с подвесом (вертикально направленной нитью). Теперь направим на поверхность зеркала луч света. Даже при незначительных движениях и поворотах зеркала отражающийся в нем луч будет заметно смещаться. Это дает нам возможность измерить вращательные колебания объекта.
Обозначив модуль кручения как L, момент инерции зеркала по отношению к оси вращения как J, а угол поворота зеркала как φ, можем записать уравнение колебаний следующего вида:
Минус в уравнении связан с направлением момента сил упругости, который стремится вернуть зеркало в равновесное положение. Теперь произведем умножение обеих частей на φ, проинтегрируем результат и получим:
Следующее уравнение является законом сохранения энергии, который будет выполняться для данных колебаний (то есть потенциальная энергия будет переходить в кинетическую и обратно). Мы можем считать эти колебания гармоническими, следовательно:
При выведении одной из формул ранее мы использовали закон равномерного распределения энергии по степеням свободы. Значит, можем записать так:
Как мы уже говорили, угол поворота можно измерить. Так, если температура будет равна приблизительно 290К, а модуль кручения L≈10-15 Н·м; φ≈4·10-6, то рассчитать значение нужного нам коэффициента можно так:
Следовательно, зная основы броуновского движения, мы можем найти постоянную Больцмана с помощью измерения макропараметров.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Краткая теория и методика выполнения работы
Удельной
теплоемкостью
вещества называется величина, равная
количеству теплоты, которую необходимо
сообщить единице массы вещества для
увеличения ее температуры на один градус
Кельвина:
. (4.1)
Теплоемкость
одного моля вещества называется молярной
теплоемкостью:
, (4.2)
где
m – масса, µ – молярная масса вещества,– число молей газа.
Значение
теплоемкости газов зависит от условий
их нагревания. В соответствии с первым
законом термодинамики количество
теплоты,
сообщенное системе, расходуется на
увеличение ее внутренней энергиии на совершение системой работыпротив внешних сил:
. (4.3)
Изменение
внутренней энергии идеального газа в
случае изменения его температурыравно:
, (4.4)
здесь
– число степеней свободы молекулы газа,
под которым подразумевается число
независимых координат, полностью
определяющих положение молекулы в
пространстве;– универсальная газовая постоянная.
При
расширении газа система совершает
работу:
. (4.5)
Если
газ нагревать при постоянном объеме
(),
тои, согласно (4.3), все полученное газом
количество теплоты расходуется только
на увеличение его внутренней энергии.
Следовательно, учитывая (4.4), молярная
теплоемкость идеального газа при
постоянном объеме будет равна:
. (4.6)
Если
газ нагревать при постоянном давление
(),
то полученное газом количество теплоты
расходуется на увеличение его внутренней
энергиии совершение газом работы:
.
Тогда
молярная теплоемкость идеального газа
при постоянном давлении определяется
следующим образом:
. (4.7)
Используя
уравнение состояния идеального газа
(уравнение Клапейрона–Менделеева),
можно показать, что для одного моля газа
справедливо соотношение:
,
поэтому:
.
Последнее выражение
называют уравнением Майера. Из него,
учитывая (4.6), получаем:
. (4.8)
Отношение
теплоемкостейобозначаюти называют показателем адиабаты или
коэффициентом Пуассона:
. (4.9)
Адиабатным
называется процесс, протекающий в
термоизолированной системе, т.е. без
теплообмена с окружающей средой,.
На
практике он может быть осуществлен в
системе, окруженной теплоизоляционной
оболочкой, но поскольку для теплообмена
необходимо некоторое время, то адиабатным
можно считать также процесс, который
протекает так быстро, что система не
успевает вступить в теплообмен с
окружающей средой.
Первый
закон термодинамики для адиабатного
процесса имеет вид.
Знак минус говорит о том, что при
адиабатном процессе система может
совершать работу только за счет внутренней
энергии. С учетом (4.4)–(4.6) имеем:
. (4.10)
Продифференцировав
уравнение Клапейрона–Менделеева,
получим:
.
Выразим
из негои подставим в формулу (4.10):
.
Выразивиз уравнения Майера и учитывая соотношение
(4.8), получим:
.
Интегрируя
данное дифференциальное уравнение при
условииполучим выражение:
.
(4.11)
Уравнение
(4.11) называется уравнением адиабаты или
уравнением Пуассона.
Метод
определения показателя адиабаты,
предложенный Клеманом и Дезормом (1819
г.), основывается на изучении параметров
некоторой массы газа, переходящей из
одного состояния в другое двумя
последовательными процессами –
адиабатным и изохорным. Эти процессы
на диаграмме–(рис. 4.1) изображены кривыми соответственно
1–2 и 2–3.
Если
в сосуд, соединенный с дифференциальным
датчиком давления, накачать воздух и
подождать до установления теплового
равновесия с окружающей средой, то в
этом начальном состоянии 1 газ имеет
параметры,,,
причем температура газа в сосуде равна
температуре окружающей среды,
а давлениенемного больше атмосферного.
Если
теперь на короткое время соединить
сосуд с атмосферой, то произойдет
адиабатное расширение воздуха. При этом
воздух в сосуде перейдет в состояние
2, его давление понизится до атмосферного.
Масса воздуха, оставшегося в сосуде,
которая в состоянии 1 занимала часть
объема сосуда, расширяясь, займет весь
объем.
При этом температура воздуха, оставшегося
в сосуде, понизится до.
Поскольку процесс 1–2 – адиабатный, к
нему можно применить уравнение Пуассона
(4.11):
или.
Отсюда:
. (4.12)
После
кратковременного соединения сосуда с
атмосферой охлажденный из-за адиабатного
расширения воздух в сосуде будет
нагреваться (процесс 2–3) до температуры
окружающей средыпри постоянном объеме.
При этом давление в сосуде поднимется
до.
Поскольку
процесс 2–3 – изохорный, к нему можно
применить закон Шарля:
или
. (4.13)
Из уравнений (4.12)
и (4.13) получим:
.
Прологарифмируем
это выражение:
.
Поскольку
избыточные давленияиочень малы по сравнению с атмосферным
давлением,
а также учитывая, что при,
будем иметь:
.
Откуда:
. (4.14)
Избыточные
давленияиизмеряют с помощью дифференциального
датчика давления.
Как работает закон в реальной жизни
Используя совместно формулу расчета мощности и закон Ома, можно производить вычисления, не зная одной из величин. Самый простой пример – для лампы накаливания известны только ее мощность и напряжение. Применяя приведенные выше формулы, можно легко определить параметры нити накаливания и ток через нее.

Лампа накаливания
Сила тока формула через мощность:
I=P/U;
Сопротивление:
R=U/I.
Такой же результат можно найти из мощности, не прибегая к промежуточным расчетам:
R=U2/P.
Аналогично можно вычислить любую величину, зная только две из них. Для упрощения преобразований имеется мнемоническое отображение формул, позволяющее находить любые величины.
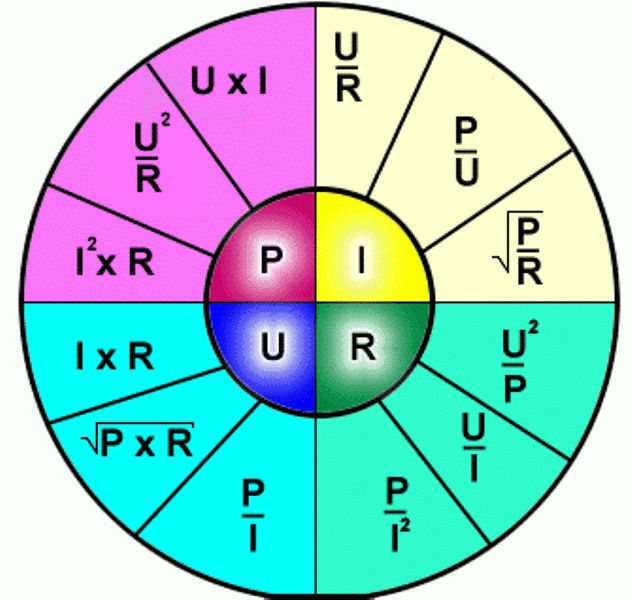
Правило для запоминания расчетов
Внимательно посмотрев на формулы, можно заметить, что, если уменьшить напряжение на лампе в два раза, ожидаемая мощность не снизится аналогично в два раза, а в четыре, согласно формуле:
P=U2/R.
Это довольно распространенная ошибка среди далеких от электротехники людей, которые неправильно соотносят мощность и напряжение, а также их действие на остальные параметры.
Кстати. Сила тока, найденная через сопротивление и напряжение, справедлива как для постоянного, так и для переменного тока, если в ней не используются такие элементы, как конденсатор или индуктивность.
Облегчить расчеты можно, используя онлайн калькулятор.
Линии напряженности
Электрическое поле не действует на органы чувств. Его мы не видим. Тем не менее распределение поля в пространстве можно сделать видимым. Английский физик Майкл Фарадей в 1845 году предложил изображать электрическое поле с помощью силовых линий и получал своеобразные карты, или диаграммы поля.
Силовая линия (или линия напряженности) — это воображаемая направленная линия в пространстве, касательная к которой в каждой точке совпадают с направлением вектора напряженности в этой точке (рис. 5).
- Рис. 5
- Рис. 6
По картине силовых линий можно судить не только о направлении вектора , но и о его значении. Действительно, для точечных зарядов напряженность поля увеличивается по мере приближения к заряду, а силовые линии при этом сгущаются (рис. 6). Где силовые линии гуще там напряженность больше и наоборот.
Число силовых линий, приходящихся на поверхность единичной площади, расположенную нормально к силовым линиям, пропорционально модулю напряженности.
Картины силовых линий
Построить точную картину силовых линий заряженного тела – сложная задача. Нужно сначала вычислить напряженность поля Е
(х, у, z ) как функцию координат. Но этого еще мало. Остается непростая задача проведения непрерывных линий так, чтобы в каждой точке линии касательная к ней совпадала с направлением напряженности \(~\vec E\) . Такую задачу проще всего поручить компьютеру, работающему по специальной программе.
Впрочем, строить точную картину распределения силовых линий не всегда необходимо. Иногда достаточно рисовать приближенные картины, не забывая что:
- силовые линии — это незамкнутые линии: они начинаются на поверхности положительно заряженных тел (или в бесконечности) и оканчиваются на поверхности отрицательно заряженных тел (или в бесконечности);
- силовые линии не пересекаются, так как в каждой точке поля вектор напряженности имеет лишь одно направление;
- между зарядами силовые линии нигде не прерываются.
На рисунках 7–10 изображены картины силовых линий: положительно заряженного шарика (рис. 7); двух разноименно заряженных шариков (рис. 8); двух одноименно заряженных шариков (рис. 9); двух пластин, заряды которых равны по модулю и противоположны по знаку (рис. 10).
- Рис. 7
- Рис. 8
- Рис. 9
- Рис. 10
На рисунке 10 видно, что в пространстве между пластинами вдали от краев пластин силовые линии параллельны: электрическое поле здесь одинаково во всех точках.
Электрическое поле, напряженность которого одинакова во всех точках пространства, называется однородным .
Не следует думать, что линии напряженности – это существующие в действительности образования вроде растянутых упругих нитей или шнуров, как предполагал сам Фарадей. Линии напряженности лишь помогают представить распределение поля в пространстве и не более реальны, чем меридианы и параллели на земном шаре.
Однако силовые линии можно сделать «видимыми». Для этого нужно металлические тела (электроды) соединить с полюсами электростатической машины и погрузить в вязкий диэлектрик (например, в касторовое или вазелиновое масло). В эту жидкость надо насыпать и хорошо перемешать продолговатые частицы изолятора (например, вискозы, асбеста, манной крупы, семян или мелко настриженный волос). При заряжении электродов в жидкости создается достаточно сильное электрическое поле. Под влиянием электрического поля частицы диэлектрика поляризуются: на их концах появляются заряды противоположного знака. Частицы поворачиваются во внешнем поле вдоль линий напряженности, и заряды на их концах взаимодействуют друг с другом. Разно именные заряды притягиваются, а одноименные отталкиваются. В результате частицы диэлектрика вы страиваются вдоль силовых линий (рис. 11).
- а
- б
- в
Рис. 11. Демонстрация силовых линий с помощью нитей вискозы
Поляризация диэлектрика
Давайте возьмем два, на первый взгляд, одинаковых задания из ЕГЭ.
Задание 1
Если к незаряженному металлическому шару поднести, не касаясь, точечный положительный заряд, то на стороне шара, ближайшей к заряду, появится отрицательный заряд. Как называется это явление?
Мы только что это разобрали: то электростатическая индукция.
Задание 2
Если к незаряженному диэлектрическому шару поднести, не касаясь, точечный положительный заряд, то на стороне шара, ближайшей к заряду, появится отрицательный заряд. Как называется это явление?
Кажется, что очень похоже на электростатическую индукцию, но это явление будет называться поляризация. В чем разница:
В первом случае — это проводник, а во втором — диэлектрик. Если не вдаваться в подробности, то поляризация диэлектрика — процесс, очень похожий по природе своей на электростатическую индукцию, только происходит в непроводящих материалах.
Соответствие физической величины в системе СИ
Основные величины
| Величина | Символ | Единица СИ | Описание |
| Длина | l | метр (м) | Протяжённость объекта в одном измерении. |
| Вес | m | килограмм (кг) | Величина, определяющая инерционные и гравитационные свойства тел. |
| Время | t | секунда (с) | Продолжительность события. |
| Сила электрического тока | I | ампер (А) | Протекающий в единицу времени заряд. |
|
Термодинамическая температура |
T | кельвин (К) | Средняя кинетическая энергия частиц объекта. |
| Сила света |
Iv |
кандела (кд) | Количество световой энергии, излучаемой в заданном направлении в единицу времени. |
| Количество вещества | ν | моль (моль) | Количество частиц, отнесенное к количеству атомов в 0,012 кг12C |
Производные величины
| Величина | Символ | Единица СИ | Описание |
| Площадь | S | м2 | Протяженность объекта в двух измерениях. |
| Объём | V | м3 | Протяжённость объекта в трёх измерениях. |
| Скорость | v | м/с | Быстрота изменения координат тела. |
| Ускорение | a | м/с² | Быстрота изменения скорости объекта. |
| Импульс | p | кг·м/с | Произведение массы и скорости тела. |
| Сила |
F |
кг·м/с2 (ньютон, Н) | Действующая на объект внешняя причина ускорения. |
| Механическая работа | A | кг·м2/с2 (джоуль, Дж) | Скалярное произведение силы и перемещения. |
| Энергия | E | кг·м2/с2 (джоуль, Дж) | Способность тела или системы совершать работу. |
| Мощность | P | кг·м2/с3 (ватт, Вт) | Скорость изменения энергии. |
| Давление | p | кг/(м·с2) (паскаль, Па) | Сила, приходящаяся на единицу площади. |
| Плотность | ρ | кг/м3 | Масса на единицу объёма. |
| Поверхностная плотность | ρA | кг/м2 | Масса на единицу площади. |
| Линейная плотность | ρl | кг/м | Масса на единицу длины. |
| Количество теплоты | Q | кг·м2/с2 (джоуль, Дж) | Энергия, передаваемая от одного тела к другому немеханическим путём |
| Электрический заряд | q | А·с (кулон, Кл) | |
| Напряжение | U | м2·кг/(с3·А) (вольт, В) | Изменение потенциальной энергии, приходящееся на единицу заряда. |
| Электрическое сопротивление | R | м2·кг/(с3·А2) (ом, Ом) | сопротивление объекта прохождению электрического тока |
| Магнитный поток | Φ | кг/(с2·А) (вебер, Вб) | Величина, учитывающая интенсивность магнитного поля и занимаемую им область. |
| Частота | ν | с−1 (герц, Гц) | Число повторений события за единицу времени. |
| Угол | α | радиан (рад) | Величина изменения направления. |
| Угловая скорость | ω | с−1 (радиан в секунду) | Скорость изменения угла. |
| Угловое ускорение | ε | с−2 (радиан на секунду в квадрате) | Быстрота изменения угловой скорости |
| Момент инерции | I | кг·м2 | Мера инертности объекта при вращении. |
| Момент импульса | L | кг·м2/c | Мера вращения объекта. |
| Момент силы | M | кг·м2/с2 | Произведение силы на длину перпендикуляра, опущенного из точки на линию действия силы. |
| Телесный угол | Ω | стерадиан (ср) |
Смотри также:
- Справочные материалы по физике
- Закон Ома
- Первый закон Ньютона
- Второй закон Ньютона
- Третий закон Ньютона
- Формулы кинематики
- Формулы МКТ
Решение задач
Давайте потренируемся и рассмотрим примеры с дробями.
Задание 1
Что сделать: вычислить квадрат произведения (55 + 10)2.
Как решаем: воспользуемся формулой квадрата суммы: (55 + 10)2 = 552 + 2 * 55 * 10 + 102 = 3025 + 1100 + 100 = 4225.
Задание 2
Что сделать: упростить выражение 64 * с3 – 8.
Как решаем: применим разность кубов: 64 * с3 – 8 = (4 * с)3 – 23 = (4 * с – 2)((4 * с)2 + 4 * с * 2 + 22) = (4 * с – 2)(16 * с2 + 8 * с + 4).
Задание 3
Что сделать: раскрыть скобки (7 * y — x) * (7 * y + x).
Как решаем:
- Произведем умножение: (7 * y — x) * (7 * y + x) = 7 * y * 7 * y + 7 * y * x — x * 7 * y — x * x = 49 * y2 + 7 * y * x — 7 * y * x — x2 = 49 * y2 — x2.
- Используем формулу сокращенного умножения: (7 * y — x) * (7 * y + x) = (7 * y)2 — x2 = 49 * y2 — x2.
Многочленов бояться не стоит, просто совершайте последовательно каждое действие. С формулами решать задачки быстрее и удобнее — сохраняйте шпаргалку, запоминайте и радуйте своих учителей 🙂
https://youtube.com/watch?v=19zaWthKtYM