Как называется силовая характеристика электрического поля

Как направлен вектор электрического поля

Закон Ома для неоднородного участка

Вектор поля надо направить в сторону от положительного заряда и в обратном направлении – к отрицательному. Это определение справедливо для одной точки. Так как идеальные условия отсутствуют, в реальной ситуации приходится учитывать взаимодействие зарядов и соответствующее образование силовых линий.

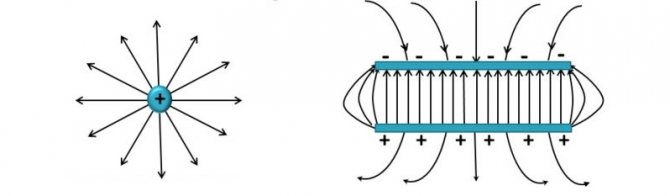
Силовые линии

Поле не является однородным, что демонстрируют с помощью разных расстояний между отдельными линиями. В примере с пластинами близкое расположение параллельных проводников позволяет обеспечить одинаковую напряженность в рабочей зоне. Все силовые линии бесконечные. Они начинаются на положительном заряде и заканчиваются на отрицательном. Таким образом, направление вектора напряженности будет всегда в сторону уменьшения потенциала.

Векторное поле

Предположим, что в углу комнаты лежит большой магнит. А мы ходим по комнате со шнурком, к одному концу которого привязан железный гвоздь. Второй конец шнурка держим в горизонтально вытянутой руке.

Расхаживая по комнате, мы заметим, что в некоторой области комнаты шнурок с гвоздем отклоняется от вертикального положения в сторону магнита.

Чем ближе мы подходим к магниту, тем сильнее он притягивает гвоздь. Тем больше усилий нужно приложить, чтобы удержать шнурок в руке.

Такие поля, наподобие поля, созданного магнитом, называют силовыми полями.

Поля силовые – это векторные поля, так как распределенная по комнате и измеренная в различных точках комнаты сила – это векторная величина.

Теперь каждой точке комнаты мы можем поставить в соответствие не только координаты точки, но и вектор F силы, действующей на гвоздь в этой точке.

Составим таблицу и запишем в нее координаты каждой выбранной точки комнаты и силы, с которой магнит действует на гвоздь в этой точке.

У вектора силы в каждой отдельной точке будут свои характеристики — длина и направление. Поэтому, таблица, содержащая информацию о силе в каждой точке комнаты, будет содержать 6 строк. Три строки – это координаты точки, и три строки – координаты вектора.

Такая таблица задает функцию, которую математики называют сокращенно «вектор-функцией».

Вектор-функцию, описывающую векторное поле, можно обозначить так:

\(\large \overrightarrow{A \left( P \right)} \) – вектор-функция. Подробнее можно записать ее таким способом:

\( A_{x}\left( x ; y ; z \right) ; A_{y}\left( x ; y ; z \right) ; A_{z}\left( x ; y ; z \right) \) – это компоненты (части) вектор функции.

\( \vec{i} ; \vec{j} ; \vec{k} \) – орты.

Обычно в школе такие функции не изучают. Но вы теперь знаете, что кроме обычных — скалярных функций, существуют вектор-функции.

Из записи видно, что векторная функция отличается от скалярной тем, что имеет три компоненты (части). Каждая компонента (часть) зависит от трех координат точки P пространства.

Как по известной напряженности вычислить силу, с которой поле действует на заряд

Если известна напряженность поля, то силу, которая действует на заряд, помещенный в это поле, можно вычислить по формуле:

\(\large q \left( \text{Кл}\right) \) – заряд, положительный, или отрицательный, помещенный в выбранную точку пространства, в которой существует электрическое поле;

Формула записана в векторном виде. Это значит, что она позволяет найти обе характеристики силы, действующей на заряд — направление вектора силы и его модуль.

Рис. 11. Направления векторов силы и напряженности совпадают для положительного заряда и направлены противоположно для отрицательного заряда

Так как напряженность входит в формулу для вычисления силы, ее называют силовой характеристикой электрического поля.

Зная силу, мы можем по вычислить ускорение заряда. А с помощью формул кинематики для равнопеременного движения, зная ускорение, можно определить заряда или траекторию его движения.

Энергия в электрическом поле

Полная энергия на единицу объема, запасенная электромагнитным полем, равна

тыЭМзнак равноε2|E|2+12μ|B|2{\ displaystyle u _ {\ text {EM}} = {\ frac {\ varepsilon} {2}} | \ mathbf {E} | ^ {2} + {\ frac {1} {2 \ mu}} | \ mathbf {B} | ^ {2}}

где ε — диэлектрическая проницаемость среды, в которой существует поле, ее магнитная проницаемость , а E и B — векторы электрического и магнитного поля.
μ{\ displaystyle \ mu}

Поскольку поля E и B связаны, было бы ошибочным разделять это выражение на «электрический» и «магнитный» вклады. В частности, электростатическое поле в любой данной системе отсчета в общем случае трансформируется в поле с магнитной составляющей в относительно движущейся системе отсчета. Соответственно, разложение электромагнитного поля на электрическую и магнитную составляющие зависит от кадра и аналогичным образом для соответствующей энергии.

Полная энергия U _EM, запасенная в электромагнитном поле в данном объеме V, равна

UЭМзнак равно12∫V(ε|E|2+1μ|B|2)dV.{\ displaystyle U _ {\ text {EM}} = {\ frac {1} {2}} \ int _ {V} \ left (\ varepsilon | \ mathbf {E} | ^ {2} + {\ frac {1 } {\ mu}} | \ mathbf {B} | ^ {2} \ right) \ mathrm {d} V \ ,.}

Потенциал

Это еще одна характеристика электрического поля. Потенциал является накопленной энергией, которую явление может использовать для перемещения зарядов. Когда тот начинает двигаться, на это тратится вот этот самый ресурс, и в конечном итоге он становится равным нулю. Накапливается он обратным образом. В качестве примера можно взять все тот же заряд, но расположенный вне электрического поля. Как только некая сила перемещает его внутрь и двигает там, появляется потенциал.

Проще всего это представить на примере обычной пружины. В своем спокойном положении она не имеет никакого потенциала и просто представляет собой изогнутый кусок металла. Но как только мы начнем сдавливать ее, начнет возникать потенциал. Если отпустить пружину, она моментально распрямится и при этом подвинет все предметы, которые сможет, расположенные на ее пути. Если вернуться к рассматриваемым электрическим полям, то в их случае потенциал будет строго соответствовать приложенным усилиям на перемещение заряда. В современной науке этот показатель измеряется вольтами.

Статическое и вихревое поле

Как упоминалось в начале статьи, электрическое поле может возникать вокруг переменного магнитного поля. Оно даже создает ток, что может быть достигнуто двумя путями:

изменением интенсивности магнитного поля, проходящего сквозь контур проводника в нем;
изменением положения самого проводника.

При этом проводнику вовсе не обязательно быть замкнутым — ток в нем все равно будет течь.

Для иллюстрации отличий статического и вихревого поля можно составить таблицу.

Параметр	Электростатическое	Вихревое
форма силовых линий	разомкнутые	замкнутые
чем создается	неподвижным зарядом	переменным магнитным потоком
источник напряженности	заряд	отсутствует
работа по перемещению в замкнутом контуре	нулевая	создает ЭДС индукции

Нельзя сказать, что первое и второе поле никак между собой не связаны. Это не так. В реальности работает такая закономерность: неподвижный заряд создает электростатическое поле, которое движет заряд в проводнике; движущийся заряд порождает постоянное магнитное поле. Если заряд движется с непостоянной скоростью и направлением, то магнитное поле становится переменным и создает вторичное электрическое. Таким образом, электрическое поле и его характеристики влияют на возможность возникновения магнитного и его параметры.

https://youtube.com/watch?v=7V4DeFyuqjs

Что это такое

Электрическое поле — это особое векторная характеристика, которая действует на все обладающие электрозарядом частицы, находящиеся в ее радиусе действия. Это электрополе входит в состав электромагнитного, то есть для него характерно отсутствие визуальной составляющей. Это значит, что ЭП нельзя увидеть глазами и оно может быть зафиксировано только в результате воздействия за заряженные частицы.

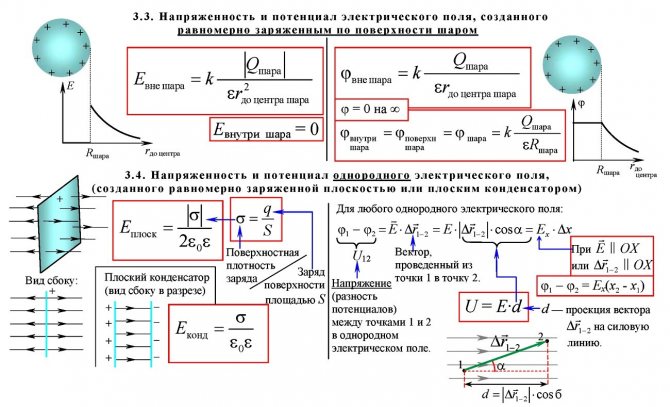
Напряженность и потенциал ЭП

Важно! На последнее реагируют все заряженные электрочастицы и тела, обладающие другими (противоположными) полюсами. Электрополе — особая форма состояния материи, которое проявляется в ускорении электрочастиц и определенных тел, которые обладают электро зарядом

К особенностям электрополя относятся:

Электрополе — особая форма состояния материи, которое проявляется в ускорении электрочастиц и определенных тел, которые обладают электро зарядом. К особенностям электрополя относятся:

Оно действует только при наличии электро заряда;
Оно не имеет определенных четких границ;
ЭП обладает определенной величиной воздействия;
Его определить только по результату его воздействия.

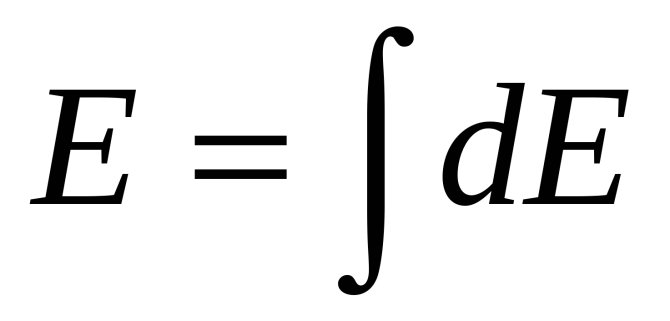
Принцип суперпозиции Характеристика ЭП неразрывно связана с зарядами. Они находятся в определенной электрочастице или теле. Преобразование ЭП происходит в двух случаях:

При появлении вокруг него электрозарядов;
При перемещении волн электромагнитной природы, которые способствуют изменению электрополя.

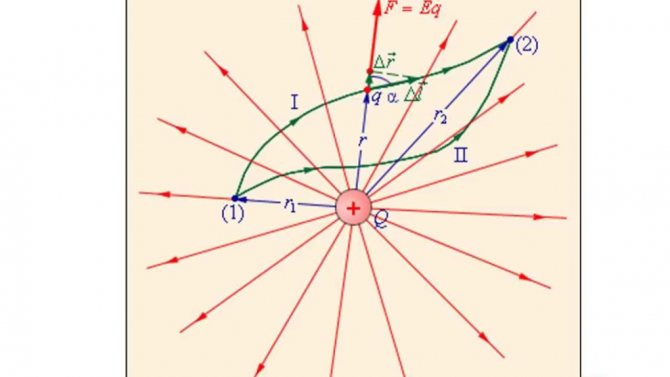
Работа сил ЭП Электрополе влияет на неподвижные относительно наблюдателя объекты в виде электро заряженных частиц или тел. В конечном итоге они получают силовое влияние. Пример воздействия ЭП можно наблюдать и в бытовой ситуации. Для этого достаточно создать электрозаряд достаточной мощности. Книги по теоретической физике предлагают для этого простейший эксперимент, когда диэлектрик натирается о шерстяное изделие. Получить электрополе вполне можно просто, взяв пластиковую шариковую ручку и потерев ее о волосы или шерсть. На ее поверхности образуется заряд, который приводит к появлению электрополя. Как следствие ручка притягивает мелкие электрочастицы в виде волос или бумаги. Если ее преподнести к мелко разорванным кусочкам бумаги, то они будут притягиваться к ней. Такой же результат можно достигнуть и при использовании пластмассовой расчески.

Вам это будет интересно Особенности расчета мощности по току и напряжению

Манипуляции с магнитными свойствами ЭП на основе железной крошки

Также примером появления электрополя в быту является образование мелких световых вспышек при снятии одежды из синтетических материалов. В результате нахождения на теле диэлектрические волокна накапливают вокруг себя различные электрозаряды. При снятии такого предмета одежды с тела ЭП подвергается различным силам воздействия, которое приводит к образованию вспышек. Особенно это характерно для зимней одежды, в частности свитеров и шарфов, которые сделаны из синтетических материалов.

Сделал открытие и впервые подтвердил наличие электрополя Майкл Фарадей — английский физик и экспериментатор. Именно он внес в физику понятие «поля» и установил основы его концепции, его физическую реальность.

Важно! Фарадей ввел понятие ЭП при исследовании диамагнетизма и парамагнетизма, когда он обнаружил небольшое отталкивание специальным магнитом ряда веществ. Напряженность электростатического поля

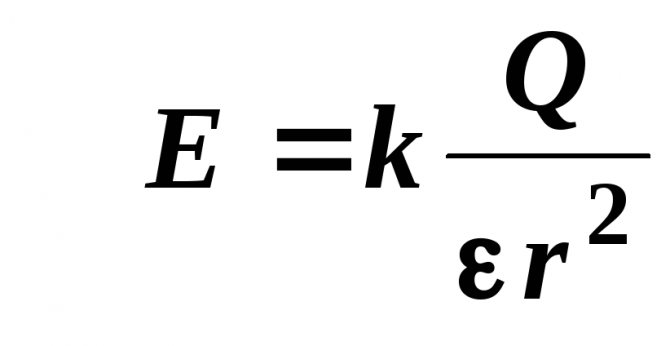
Напряженность электростатического поля

Потенциал электрического поля. Разность потенциалов

Потенциал – скалярная физическая величина, равная отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда.

Обозначение – \( \varphi \), единица измерения в СИ – вольт (В).

Потенциал \( \varphi \) является энергетической характеристикой электростатического поля.

Разность потенциалов численно равна работе, которую совершает электрическая сила при перемещении единичного положительного заряда между двумя точками поля:

Обозначение – \( \Delta\varphi \), единица измерения в СИ – вольт (В).

Иногда разность потенциалов обозначают буквой \( U \) и называют напряжением.

Важно!
Разность потенциалов \( \Delta\varphi=\varphi_1-\varphi_2 \), а не изменение потенциала \( \Delta\varphi=\varphi_2-\varphi_1 \). Тогда работа электростатического поля равна:. Важно!
Эта формула позволяет вычислить работу электростатических сил в любом поле

В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки

Важно!
Эта формула позволяет вычислить работу электростатических сил в любом поле. В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки. В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность

В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность

В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки. В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Потенциал поля точечного заряда \( q \) в точке, удаленной от него на расстояние \( r \), вычисляется по формуле:

Для наглядного представления электрического поля используют эквипотенциальные поверхности.

Важно!
Внутри проводящего шара потенциал всех точек внутри шара равен потенциалу поверхности шара и вычисляется по формуле потенциала точечного заряда (\( r =R \), где \( R \) – радиус шара). Напряженность поля внутри шара равна нулю. Эквипотенциальной поверхностью, или поверхностью равного потенциала, называется поверхность, во всех точках которой потенциал имеет одинаковое значение

Эквипотенциальной поверхностью, или поверхностью равного потенциала, называется поверхность, во всех точках которой потенциал имеет одинаковое значение.

Свойства эквипотенциальных поверхностей

Вектор напряженности перпендикулярен эквипотенциальным поверхностям и направлен в сторону убывания потенциала.
Работа по перемещению заряда по эквипотенциальной поверхности равна нулю.

В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей. Для точечного заряда эквипотенциальные поверхности представляют собой концентрические окружности.

Разность потенциалов и напряженность связаны формулой:

Из принципа суперпозиции полей следует принцип суперпозиции потенциалов:

Потенциал результирующего поля равен сумме потенциалов полей отдельных зарядов.

Важно!
Потенциалы складываются алгебраически, а напряженности – по правилу сложения векторов. Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил. Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил

Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил.

Алгоритм решения таких задач:

установить характер и особенности электростатических взаимодействий объектов системы;
ввести характеристики (силовые и энергетические) этих взаимодействий, сделать рисунок;
записать законы сохранения и движения для объектов;
выразить энергию электростатического взаимодействия через заряды, потенциалы, напряженности;
составить систему уравнений и решить ее относительно искомой величины;
проверить решение.

Напряжённость электрического поля в классической электродинамике

Для лучшего понимания темы необходимо напомнить несколько базовых определений. Существуют отрицательные и положительные электрические заряды. Каждый из них не зависит от системы координат, что подразумевает отсутствие влияния скорости. В изолированном объеме сумма зарядов не изменяется. Базовой величиной считают Кулон, который соответствует прохождению тока через единичную площадь сечения проводника за одну секунду.

Электрическое поле:

создается зарядами;
распространяется со скоростью света;
не ограничено в свободном пространстве.

Описывает напряженность электрического поля формула с векторными составляющими:

E=F/q0,

где:

E – это вектор напряженности, который зависит от координат в пространстве по осям Х, Y, Z и времени;
F – сила, оказывающая воздействие на единичный точечный заряд q0.

Вместе с вектором магнитной индукции напряженность (Е) формирует электромагнитное поле. Суммарное воздействие сил образует тензор. Вместе с зарядом это главные параметры электродинамики.

Потенциал. Эквипотенциальные поверхности.

В механике взаимодействие тел характеризует силой или потенциальной энергией. Электрическое поле, которое обеспечивает взаимодействие между электрически заряженными телами, также характеризуют двумя величинами. Напряженность электрического поля — это силовая характеристика. Теперь введем энергетическую характеристику — потенциал. С помощью этой величины можно будет сравнивать между собой любые точки электрического поля. Таким образом, потенциал как характеристика поля должен зависеть от значения заряда, содержащегося в этих точках. Поделим обе части формулы A = W₁ — W₂ на заряд q, получим

Отношение W/q не зависит от значения заряда и принимается за энергетическую характеристику, которую называют потенциалом поля в данной точке. Обозначают потенциал буквой φ.

Потенциал электрического поля φ — скалярная энергетическая характеристика поля, которая определяется отношением потенциальной энергии W положительного заряда q в данной точке поля к величине этого заряда:

Единица потенциала — вольт:

Подобно потенциальной энергии значения потенциала в данной точке зависит от выбора нулевого уровня для отсчета потенциала. Чаще всего в электродинамике за нулевой уровень берут потенциал точки, лежащей в бесконечности, а в электротехнике — на поверхности Земли.

С введением потенциала формулу для определения работы по перемещению заряда между точками 1 и 2 можно записать в виде

Поскольку при перемещении положительного заряда в направлении вектора напряженности электрическое поле выполняет положительную работу A = q (φ₁ — φ₂ )> 0, то потенциал φ₁ больше чем потенциал φ₂ . Таким образом, напряженность электрического поля направлена в сторону уменьшения потенциала.

Если заряд перемещать с определенной точки поля в бесконечность, то работа A = q (φ — φ_∞ ). Поскольку φ_∞ = 0, то A = qφ. Таким образом, величина потенциала φ определенной точки поля определяется работой, которую выполняет электрическое поле, перемещая единичный положительный заряд из этой точки в бесконечность,

Если электрическое поле создается точечным зарядом q, то в точке, лежащей на расстоянии r от него, потенциал вычисляют по формуле

По этой формуле рассчитывают и потенциал поля заряженного шара. В таком случае r — это расстояние от центра шара до выбранной точки поля. С этой формулы видно, что на одинаковых расстояниях от точечного заряда, который создает поле, потенциал одинаков. Все эти точки лежат на поверхности сферы, описанной радиусом r вокруг точечного заряда. Такую сферу называют эквипотенциальной поверхностью.

Эквипотенциальные поверхности — геометрическое место точек в электрическом поле, которые имеют одинаковый потенциал, — один из методов наглядного изображения электрических полей.

Эквипотенциальные поверхности электрических полей, созданных точечными зарядами разных знаков

Силовые линии всегда перпендикулярны эквипотенциальных поверхностей. Это означает, что работа сил поля по перемещению заряда по эквипотенциальной поверхности равна нулю.

В случае наложения электрических полей, созданных несколькими зарядами, потенциал электрического поля равен алгебраической сумме потенциалов полей, созданных отдельными зарядами, φ = φ₁ + φ₂ + φ₃ . Эквипотенциальные поверхности таких систем имеют сложную форму. Например, для системы из двух одинаковых по значению одноименных зарядов эквипотенциальные поверхности имеют вид, изображенный на рисунке. Эквипотенциальные поверхности однородного поля явлются плоскостями.

Эквипотенциальные поверхности: а — поля двух одинаковых зарядов б — однородного поля

Напряженность электрического поля

Какое поле называют электростатическим?

Определение 2

Электростатическое поле – это электрическое поле, которое окружает неподвижные и не меняющиеся со временем заряды.

Очень часто в контексте темы электростатическое поле будет именоваться электрическим для краткости.

Электрическое поле может быть создано сразу несколькими заряженными телами. Такое поле также можно исследовать с помощью пробного заряда. В этом случае мы будем оценивать результирующую силу, которая будет равна геометрической сумме сил каждого из заряженных тем в отдельности.

Определение 3

Напряженность электрического поля, которая создается в определенной точке пространства системой зарядов, будет равна векторной сумме напряженностей электрических полей:

E→=E1→+E2→+…

Электрическое поле подчиняется принципу суперпозиции.

Определение 4

Согласно формуле, напряженность электростатического поля, которое создается точечным зарядом Q на расстоянии r от него, в соответствии с законом Кулона, будет равна по модулю:

E=14πε·Qr2.

Это поле называется кулоновским.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

В кулоновском поле направление вектора E⇀ зависит от знака заряда Q: если Q>, то вектор E⇀ направлен по радиусу от заряда, если Q<, то вектор E⇀ направлен к заряду.

Обратимся к иллюстрации. На рисунке для большей наглядности мы используем силовые линии электрического поля. Они проходят таким образом, чтобы направление вектора E⇀ в каждой из точек пространства совпадало с направлением касательной к силовой линии. Густота силовых линий соответствует модулю вектора напряженности поля.

Рисунок 1.2.1. Силовые линии электрического поля.

Мы можем использовать как положительные, так и отрицательные точечные заряды. Оба эти случая мы изобразили на рисунке. Электростатическое поле, которое создается системой зарядов, мы можем представить как суперпозицию кулоновских полей точечных зарядов. В связи с этим мы можем рассматривать поля точечных зарядов как элементарные структурные единицы любого электрического поля.

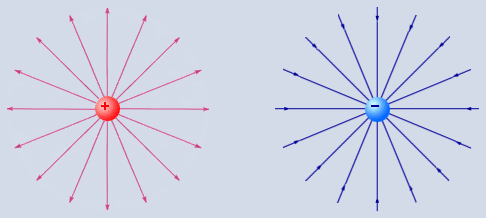
Рисунок 1.2.2. Силовые линии кулоновских полей.

Кулоновское поле точечного заряда Q удобно записать в векторной форме. Для этого нужно провести радиус-вектор r→от заряда Q к точке наблюдения. Тогда при Q> вектор E→ параллелен r→, а при Q< вектор E→ антипараллелен r→.

Следовательно можно записать:

E→=14πε·Qr3r→,

где r – модуль радиус-вектора r→.

По заданному распределению зарядов можно определить электрическое поле E→. Такие задачи часто встречаются в таком разделе физики как электростатика. Рассмотрим пример такой задачи.

Пример 1

Предположим, что нам нужно найти электрическое поле длинной однородно заряженной нити на расстоянии R от нее. Для большей наглядности мы привели схему на рисунке ниже.

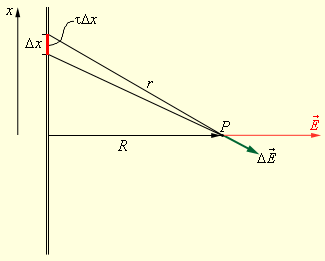
Рисунок 1.2.3. Электрическое поле заряженной нити.

Поле в точке наблюдения P может быть представлено в виде суперпозиции кулоновских полей, создаваемых малыми элементами Δx нити, с зарядом τΔx, где τ – заряд нити на единицу длины. Задача сводится к суммированию (интегрированию) элементарных полей ∆E→. Результирующее поле оказывается равным

E=τ2πεR.

Вектор E→ везде направлен по радиусу R→. Это следует из симметрии задачи.

Даже в таком простом примере вычисления могут быть достаточно громоздкими. Упростить математические расчеты позволяет теорема Гаусса, которая выражает фундаментальное свойство электрического поля.

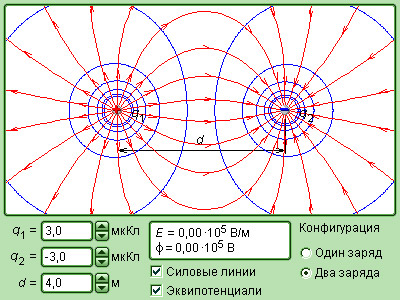
Рисунок 1.2.4. Модель электрического поля точечных зарядов.

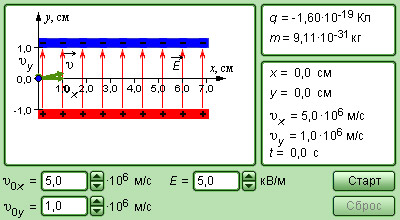
Рисунок 1.2.5. Модель движения заряда в электрическом поле.