Некоторые свойства
Из аксиом видно, что наименьшим элементом является 0, наибольшим является 1, а дополнение ¬a любого элемента a однозначно определено. Для всех a и b из A верны также следующие равенства:
| a∨a=a{\displaystyle a\lor a=a} | a∧a=a{\displaystyle a\land a=a} | |
| a∨=a{\displaystyle a\lor 0=a} | a∧1=a{\displaystyle a\land 1=a} | |
| a∨1=1{\displaystyle a\lor 1=1} | a∧={\displaystyle a\land 0=0} | |
| ¬=1{\displaystyle \lnot 0=1} | ¬1={\displaystyle \lnot 1=0} | дополнение 0 есть 1 и наоборот |
| ¬(a∨b)=¬a∧¬b{\displaystyle \lnot (a\lor b)=\lnot a\land \lnot b} | ¬(a∧b)=¬a∨¬b{\displaystyle \lnot (a\land b)=\lnot a\lor \lnot b} | законы де Моргана |
| ¬¬a=a{\displaystyle \lnot \lnot a=a}. | инволютивность отрицания, закон снятия двойного отрицания. |
Математика и логика
Известнейший Готфрид Вильгельм Лейбниц сформулировал понятие «математическая логика», задачи которой были доступны для понимания только узкому кругу ученых. Особого интереса это направление не вызывало, и до середины XIX века о математической логике знали немногие.
Большой интерес в научных сообществах вызвал спор, в котором англичанин Джордж Буль заявил о своем намерении создать раздел математики, не имеющий абсолютно никакого практического применения. Как мы помним из истории, в это время активно развивалось промышленное производство, разрабатывались всевозможные вспомогательные машины и станки, т. е. все научные открытия имели практическую направленность.
Забегая вперед, скажем, что булева алгебра – самая используемая в современном мире часть математики. Так что спор свой Буль проиграл.
Обобщения
Удаление требования существования единицы из аксиом булевой алгебры дает «обобщенные булевы алгебры». Формально дистрибутивная решетка B является обобщенной булевой решеткой, если она имеет наименьший элемент 0 и для любых элементов a и b в B, таких, что a ≤ b , существует элемент x такой, что a ∧ x = 0 и a ∨ x = б. Определяя a ∖ b как единственный x такой, что (a ∧ b) ∨ x = a и (a ∧ b) ∧ x = 0, мы говорим, что структура (B, ∧, ∨, ∖, 0) является обобщенной булевой алгебры , а (B, ∨, 0) — обобщенная булева полурешетка . Обобщенные булевы решетки — это в точности идеалы булевых решеток.
Структура, удовлетворяющая всем аксиомам булевых алгебр, за исключением двух аксиом дистрибутивности, называется решеткой с ортодополнениями . Ортодополняемые решетки естественным образом возникают в квантовой логике как решетки замкнутых подпространств для сепарабельных гильбертовых пространств .
Аксиоматизация
В 1933 году американский математик Хантингтон предложил следующую аксиоматизацию для булевых алгебр:
- Аксиома коммутативности: x + y = y + x.
- Аксиома ассоциативности: (x + y) + z = x + (y + z).
- Уравнение Хантингтона: n(n(x) + y) + n(n(x) + n(y)) = x.
Здесь использованы обозначения Хантингтона: + означает дизъюнкцию, n — отрицание.
Герберт Роббинс поставил следующий вопрос: можно ли сократить последнюю аксиому так, как написано ниже, то есть будет ли определённая выписанными ниже аксиомами структура булевой алгеброй?
Аксиоматизация алгебры Роббинса:
- Аксиома коммутативности: x + y = y + x.
- Аксиома ассоциативности: (x + y) + z = x + (y + z).
- Уравнение Роббинса: n(n(x + y) + n(x + n(y))) = x.
Этот вопрос оставался открытым с 1930-х годов и был любимым вопросом Тарского и его учеников.
В 1996 году Вильям МакКьюнruen, используя некоторые полученные до него результаты, дал утвердительный ответ на этот вопрос. Таким образом, любая алгебра Роббинса является булевой алгеброй.
Операция И — логическое умножение (конъюнкция)
Логическая операция И выполняет функцию пересечения двух высказываний (аргументов), в качестве которых может быть и простое, и сложное логическое выражение. Результатом операции И является выражение, которое будет истинным тогда и только тогда, когда истинны оба исходных выражения.
Применяемые обозначения: А и В, А ? В, A & B, A and B.
Результат операции И определяется следующей таблицей истинности:
| A | B | А и B |
| 1 | ||
| 1 | ||
| 1 | 1 | 1 |
Результат операции И истинен тогда и только тогда, когда истинны одновременно высказывания А и В, и ложен во всех остальных случаях.
Приведем примеры логического умножения.
1. Рассмотрим высказывание «Умение и настойчивость приводит к достижению цели». Достижение цели возможно только при одновременной истинности двух предпосылок — умения И настойчивости.
Логическую операцию И можно сравнить с последовательным соединением лампочек в гирлянде. При наличии хотя бы одной неработающей лампочки электрическая цепь оказывается разомкнутой, то есть гирлянда не работает. Ток протекает только при одном условии — все составляющие цепи должны быть исправны.
Операция «ЕСЛИ-ТО» — логическое следование (импликация)
Эта операция связывает два простых логических выражения, из которых первое является условием, а второе — следствием из этого условия.
Применяемые обозначения:
если А, то В; А влечет В; if A then В; А? В.
Таблица истинности:
| A | B | А ? B |
| 1 | ||
| 1 | 1 | |
| 1 | ||
| 1 | 1 | 1 |
Результат операции следования (импликации) ложен только тогда, когда предпосылка А истинна, а заключение В (следствие) ложно.
Приведем примеры операции следования.
1. Рассмотрим высказывание «Если идет дождь, то на улице сыро». Здесь исходные высказывания «Идет дождь» и «На улице сыро». Если не идет дождь и не сыро на улице, результат операции следования — истина. На улице может быть сыро и без дождя, например, когда прошла поливочная машина или дождь прошел накануне. Результат операции ложен только тогда, когда дождь идет, а на улице не сыро.
2. Рассмотрим два высказывания: А {х делится на 9}, В {х делится на 3}. Операция А ? В означает следующее: «Если число делится на 9, то оно делится и на 3». Рассмотрим возможные варианты:
? А — ложно, В — ложно (1-я строка таблицы истинности). Можно найти такие числа, для которых истиной является высказывание «если А — ложно, то и В — ложно». Например, х = 4, 17, 22.
? А — ложно, В — истинно (2-я строка таблицы истинности). Можно найти такие числа, для которых истиной является высказывание «если А — ложно, то В — истинно». Например, х = б, 12, 21.
? А — истинно, В — ложно (3-я строка таблицы истинности). Невозможно найти такие числа, которые делились бы на 9, но не делились на 3. Истинная предпосылка не может приводить к ложному результату импликации.
? А — истинно, В — истинно (4-я строка таблицы истинности). Можно найти такие числа, для которых истиной является высказывание «если А — истинно, то и В — истинно». Например, х = 9, 18, 27.
Булевы кольца
Каждая булева алгебра ( A , ∧, ∨) порождает кольцо ( A , +, ·), определяя a + b : = ( a ∧ ¬ b ) ∨ ( b ∧ ¬ a ) = ( a ∨ b ) ∧ ¬ ( a ∧ b ) (эта операция называется симметричной разностью в случае множеств и в случае логики) и a · b : = a ∧ b . Нулевой элемент этого кольца совпадает с нулем булевой алгебры; мультипликативный единичный элемент кольца — это единица булевой алгебры. Это кольцо обладает тем свойством, что a · a = a для всех a из A ; кольца с этим свойством называются булевыми кольцами .
И наоборот, если дано булево кольцо A , мы можем превратить его в булеву алгебру, определив x ∨ y : = x + y + ( x · y ) и x ∧ y : = x · y . Поскольку эти две конструкции обратны друг другу, мы можем сказать, что каждое булево кольцо возникает из булевой алгебры, и наоборот. Более того, отображение f : A → B является гомоморфизмом булевых алгебр тогда и только тогда, когда оно является гомоморфизмом булевых колец. В категории булевых колец и булевых алгебр эквивалентны.
Hsiang (1985) предложил алгоритм, основанный на правилах, для проверки того, обозначают ли два произвольных выражения одно и то же значение в каждом булевом кольце. В более общем плане Буде, Жуанно и Шмидт-Шаус (1989) дали алгоритм для между произвольными выражениями булевых колец. Используя подобие булевых колец и булевых алгебр, оба алгоритма находят применение в автоматическом доказательстве теорем .
Идеалы и фильтры
Идеал булевой алгебры A есть подмножество I , что для всех х , у в I мы имеем х ∨ у в I и для всех а в А мы имеем ∧ х в I . Это понятие идеального совпадает с понятием кольца идеал в булевой кольце A . Идеал I в А называется простой , если I ≠ A , и если ∧ б в I всегда подразумевает в I или б в I . Кроме того, для любого a ∈ A имеем a ∧ -a = 0 ∈ I и тогда a ∈ I или -a ∈ I для любого a ∈ A , если I простое число. Идеал I кольца A называется максимальным, если I ≠ A и если единственный идеал, надлежащим образом содержащий I, — это сам A. Для идеального I , если ∉ я и -a ∉ я , то я ∪ { } или я ∪ { -a } должным образом содержится в другом идеала J . Следовательно, I не является максимальным, и поэтому понятия простого идеала и максимального идеала эквивалентны в булевых алгебрах. Кроме того, эти понятия совпадают с кольцевой теорико одними из простого идеала и максимального идеала в булевом кольце А .
Двойник идеала — это фильтр . Фильтр булевой алгебры А является подмножеством р такое , что для всех х , у в р мы имеем х ∧ у в р и для всех а в А мы имеем ∨ х в р . Двойственный к максимальному (или простому ) идеалу в булевой алгебре является ультрафильтром . В качестве альтернативы ультрафильтры можно описать как двузначные морфизмы из A в двухэлементную булеву алгебру. Оператор каждый фильтр в булевой алгебре может быть продолжен до ультрафильтра называется и не могут быть доказаны в ZF , если ZF является последовательным . В ZF это строго слабее, чем выбранная аксиома . Теорема об ультрафильтре имеет много эквивалентных формулировок: каждая булева алгебра имеет ультрафильтр , каждый идеал в булевой алгебре может быть расширен до простого идеала и т. Д.
Логическая функция «НЕ» (отрицание)
Функция «Логическое НЕ» — это просто инвертор с одним входом, который изменяет вход логического уровня «1» на выход логического уровня «0» и наоборот.
«Функция логического НЕ» называется так, потому что ее выходное состояние НЕсовпадает с его входным состоянием с ее логическим выражением, обычно обозначаемым чертой или линией ( ¯ ) над его входным символом, который обозначает операцию инвертирования (отсюда ее название как инвертор).
Поскольку логическое «НЕ» выполняет логическую функцию инвертирования или комплементационной, их чаще называют инверторами, поскольку они инвертируют сигнал. В логических схемах это отрицание может быть представлено нормально замкнутым переключателем.
Представление функции «НЕ» на схеме
Если A означает, что переключатель замкнут, то «НЕ» A или А (с верхней чертой) говорит, что переключатель НЕ замкнут или, другими словами, он разомкнут. Функция логического НЕ имеет один вход и один выход, как показано на рисунке.
Таблица истинности для функции «НЕ»
Индикатор инверсии для логической функции «НЕ» является символом «пузыря», ( O) на выходе (или входе) символа логических элементов. В булевой алгебре инвертирующая логическая функция «НЕ» следует Закону дополнения, создающему инверсию.
Логические «НЕ» элементы или «Инверторы», как их чаще называют, могут быть связаны со стандартными элементами «И» и» ИЛИ» для создания элементов «НЕ И» и «НЕ ИЛИ» соответственно. Инверторы также могут использоваться для генерации «дополнительных» сигналов в более сложных декодерах / логических схемах, например, дополнение логики A — это «НЕ» A , а два последовательно соединенных инвертора дают двойную инверсию, которая выдает на своем выходе исходное значение A.
При проектировании логических схем вам может понадобиться только один или два инвертора в вашей конструкции, но если у вас нет места или денег для выделенного чипа инвертора, такого как 74LS04. Тогда вы можете легко заставить логику «НЕ» функционировать, используя любые запасные элементы «НЕ А» или «НЕ ИЛИ», просто соединяя их входы вместе, как показано ниже.
Обозначение
Операторы булевых алгебр отмечаются по-разному. В логической интерпретации как конъюнкции, дизъюнкции и отрицания, они записываются как , и и вербализуются , как И, ИЛИ, НЕ или И, ИЛИ, НЕ. В теоретико-множественной интерпретации как пересечение, объединение и дополнение они записываются как , и ( ). Для того, чтобы подчеркнуть абстракции в общей булевой алгебре, пары символов , такие как , или , также используются.
∧{\ Displaystyle \ клин}∨{\ displaystyle \ lor}¬{\ displaystyle \ neg}∩{\ displaystyle \ cap}∪{\ Displaystyle \ чашка}∁{\ displaystyle ^ {\ complement}}А.∁{\ Displaystyle А ^ {\ дополнение}}⊓{\ displaystyle \ sqcap}⊔{\ displaystyle \ sqcup}*{\ displaystyle \ ast}∘{\ displaystyle \ circ}
Математики иногда пишут «·» вместо И и «+» вместо ИЛИ (из-за их отдаленного сходства с умножением и сложением других алгебраических структур) и НЕ обозначают чертой, тильдой ~ или конечным штрихом . Это обозначение также в цифровой алгебре переключения для описания схем логических функций обычно; там часто используются определяемые ссылки NAND (NOT AND), NOR (NOT OR) и XOR (EXCLUSIVE OR).
В этой статье используются символы операторов , и .
∧{\ Displaystyle \ клин}∨{\ displaystyle \ lor}¬{\ displaystyle \ neg}
Ассоциативные операции.
Ассоциативными называют операции, которые можно выполнять в
произвольном порядке. По схеме:
(x + y) + z = x + (y + z), где + — некоторая операция.
Здесь приведена программа на языке C,
позволяющая увидеть таблицу истинности всех 16 бинарных логических
операций и проверить их ассоциативность путем перебора вариантов.
Проверка показывает ассоциативность всего лишь для 4 операций
«&», «», «», «» из 10 нетривиальных.
(x & y) & z = x & (y & z)(x y) z = x (y z)(x y) z = x (y z)(x y) z = x (y z)
Из комутативности и ассоциативности этих четырех операций
следует, что если мы имеем много переменных подряд, соединенных
такой операцией, то переменные можно переставлять в любом
порядке, а значит скобки для указания порядка не обязательны:
(a & b) & (c & d) = a & d & c & b.
Программирование 1С: логический вычислитель Светофор
Идея проста – мы имеем 3 реквизита типа «Булево»:
- Красный
- Желтый
- Зеленый
Соответственно каждый этот реквизит может быть либо «активен» (то есть иметь значение Истина), либо «отключен» (то есть иметь значение Ложь).
Перенесем реквизиты на форму обработки.
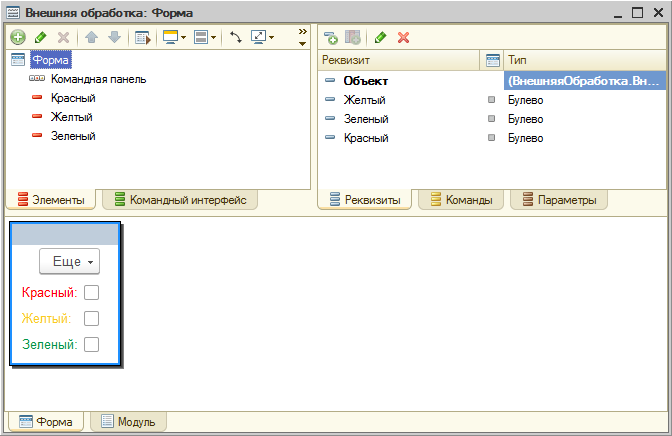
Обратите внимание ؘ– мы использовали инструменты оформления элементов. В данном случае мы изменили цвет текста в настройках поля
Далее создадим реквизит типа Строка, который назовем Реакция пешехода и также перенесем его на форму. Задача нашей обработки – при вводе определенной комбинации «цветов светофора», выводить в стоке результат – ожидаемое действие пешехода.
Для чистоты процедуры мы создадим обработчик события, который будет обнулять булевы реквизиты при открытии обработки. Создаем обработчик &НаКлиенте, который запускается ПриОткрытии через контекстное меню по щелчку на форме.

Конфигуратор автоматически подставил часть кода, которая задает условие запуска обработчика..
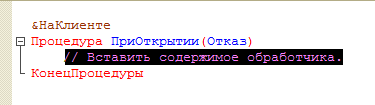
Задаем содержимое обработчика:
Красный=Ложь;Желтый=Ложь;Зеленый=Ложь;
Обратите внимание, что значение булева реквизита «Ложь» нельзя брать в кавычки, иначе программа прочитает его как Строку. Полный курс программиста 1С – с нуля до разработчика, способного решать практические учетные задачи в любой области
Полный курс программиста 1С – с нуля до разработчика, способного решать практические учетные задачи в любой области.
Логические умножение и сложение
Логическое И называют операцией конъюнкции. Что это значит? Во-первых, что применить ее можно к двум операндам, т. е. И – бинарная операция. Во-вторых, что только в случае истинности обоих операндов (и А, и Б) истинно и само выражение. Пословица «Терпение и труд все перетрут» предполагает, что только оба фактора помогут человеку справиться со сложностями.
Для записи используются символы: A∧Б, A⋅Б или A&&Б.
Конъюнкция аналогична умножению в арифметике. Иногда так и говорят – логическое умножение. Если перемножить элементы таблицы по строкам, мы получим результат, аналогичный логическому размышлению.
Дизъюнкцией называют операцию логического ИЛИ. Она принимает значение истинности тогда, когда хотя бы одно из высказываний истинно (или А, или Б). Записывается это так: A∨Б, A+Б или A||Б. Таблицы истинности для этих операций такие:
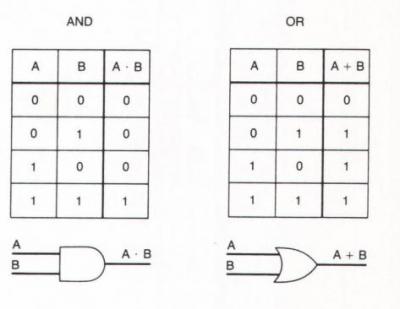
Дизъюнкция подобна арифметическому сложению. Операция логического сложения имеет только одно ограничение: 1+1=1. Но мы же помним, что в цифровом формате математическая логика ограничена 0 и 1 (где 1 – истина, 0 — ложь). Например, утверждение «в музее можно увидеть шедевр или встретить интересного собеседника» означает, что можно посмотреть произведения искусства, а можно познакомиться с интересным человеком. В то же время, не исключен вариант одновременного свершения обоих событий.
Функции импликации и эквивалентности
Как мы уже говорили, помимо основных логических операций математическая логика и теория алгоритмов использует производные. Чаще всего применяются импликация и эквивалентность.
Импликация, или логическое следование – это высказывание, в котором одно действие является условием, а другое – следствием его выполнения. Иными словами, это предложение с предлогами «если. то». «Любишь кататься, люби и саночки возить». Т. е. для катания необходимо затянуть санки на горку. Если же нет желания съехать с горы, то и санки таскать не приходится. Записывается это так: A→Б или A⇒Б.
Эквивалентность предполагает, что результирующее действие наступает только в том случае, когда истиной являются оба операнда. Например, ночь сменяется днем тогда (и только тогда), когда солнце встает из-за горизонта. На языке математической логики это утверждение записывается так: A≡Б, A⇔Б, A==Б.
Логическая функция «ИЛИ» (сложение)
Функция логического «ИЛИ» заявляет, что выходное действие станет ИСТИНОЙ, если одно «ИЛИ» больше событий ИСТИНЫ, но порядок, в котором они происходят, не имеет значения, поскольку он не влияет на конечный результат.
Так , например, А + В = В + А . В булевой алгебре функция логического «ИЛИ» подчиняется коммутативному закону так же, как и для логической функции «И», что позволяет изменять положение любой переменной.
Логика или логическое выражение, данное для логического элемента «ИЛИ», является логическим выражением, которое обозначается знаком плюс, ( + ). Таким образом, 2-входной ( АВ ) Логический элемент «ИЛИ» имеет выход термин, представленный булевой выражением: A + B = Q .
Представление функции «ИЛИ» на схеме
Здесь два переключателя А и B соединены параллельно и, либо переключатель A «ИЛИ» переключатель B может быть закрыт, чтобы включить лампу. Другими словами, выключатель может быть замкнут, либо быть на логике «1», чтобы лампа была включена.
Тогда этот тип логического элемента генерирует и выводит только тогда, когда присутствует «ЛЮБОЙ» из его входов, и в терминах Булевой алгебры выход будет ИСТИНА, если любой из его входов ИСТИНЕН. В электрическом смысле логическая функция «ИЛИ» равна параллельной цепи.
Как и в случае с функцией «И», есть два переключателя, каждый с двумя возможными положениями, открытыми или закрытыми, поэтому будет 4 различных способа расположения переключателей.
Таблица истинности для функции «ИЛИ»
Логические «ИЛИ» элементы доступны в виде стандартных пакетов ic, таких как общие TTL 74LS32 Четырехместные 2-входные положительные «ИЛИ» элементы. Как и в предыдущем логическом элементе «И», «ИЛИ» также может быть «каскадно» соединен для создания цепей с большим количеством входов, таких как системы охранной сигнализации (зона A или зона B или зона C и т.д.).
Представление булевых функций[править]
Теорема Поста открывает путь к представлению булевых функций синтаксическим способом, который в ряде случаев оказывается намного удобнее чем таблицы истинности. Отправной точкой здесь служит нахождение некоторой полной системы функций . Тогда каждая булева функция сможет быть представлена некоторым термом в сигнатуре , который в данном случае называют также формулой. Относительно выбраной системы функций полезно знать ответы на следующие вопросы:
- Как построить по данной функции представляющую её формулу?
- Как проверить, что две разные формулы эквивалентны, то есть задают одну и ту же функцию?
- Как по данной функции построить представляющую её формулу с теми или иными заданными свойствами (например, наименьшего размера), и возможно ли это?
Положительные ответы на эти и другие вопросы существенно увеличивают прикладное значение выбранной системы функций.
Дизъюнктивная нормальная форма (ДНФ)править
- Основная статья: ДНФ
| Определение: |
| Дизъюнктивная нормальная форма (ДНФ) (англ. disjunctive normal form, DNF) — нормальная форма, в которой булева функция задана как дизъюнкция некоторого числа простых конъюнктов. |
Любая булева формула благодаря использованию закона двойного отрицания, закона де Моргана и закона дистрибутивности может быть записана в ДНФ.
Примеры ДНФ:
.
.
Конъюнктивная нормальная форма (КНФ)править
- Основная статья: КНФ
| Определение: |
| Конъюнктивная нормальная форма, КНФ (англ. conjunctive normal form, CNF) — нормальная форма, в которой булева функция имеет вид конъюнкции нескольких простых дизъюнктов. |
Любая булева формула с помощью использования закона двойного отрицания, закона де Моргана и закона дистрибутивности может быть записана в КНФ.
Пример КНФ:
Полином Жегалкинаправить
- Основная статья: Полином Жегалкина
| Определение: |
| Полином Жегалкина (англ. Zhegalkin polynomial) — полином с коэффициентами вида и , где в качестве произведения берётся конъюнкция, а в качестве сложения исключающее или. |
Полином Жегалкина имеет следующий вид:
С помощью полинома Жегалкина можно выразить любую булеву функцию, так как он строится из следующего набора функций: , который, в свою очередь, по теореме Поста является полным.
Примеры:
Схемы из функциональных элементовправить
- Основная статья: Реализация булевой функции схемой из функциональных элементов
| Определение: |
|
Схема из функциональных элементов, логическая схема (англ. logic diagram) — размеченный ориентированный граф без циклов, в некотором базисе , в котором:
1. вершины, в которые не входят ребра, называются входами схемы, и каждая из них помечена некоторой переменной (разным вершинам соответствуют разные переменные); 2. в каждую из остальных вершин входит одно или более ребер (зависит от выбранного базиса ). Такие вершины называются функциональными элементами и реализуют какую-либо булеву функцию из базиса . |
Отождествление переменных осуществляется при помощи ветвления проводников.
Чтобы осуществить подстановку одной функции в другую нужно выход логического элемента, который реализует первую функцию, направить на вход логического элемента, который реализует вторую функцию.
Некоторые логические элементы:
| И | ИЛИ | НЕ | Штрих Шеффера | Стрелка Пирса |
|---|---|---|---|---|
Определение
Булева алгебра является шести- кортеж , состоящий из множества A , оснащен двумя бинарными операциями ∧ ( так называемые «концами» или «и»), ∨ ( так называемый «присоединиться» или «или»), А унарная операция ¬ ( так называемый » дополнять или не дополнять) и два элемента 0 и 1 в A (называемые «нижний» и «верхний», или «наименьший» и «наибольший» элементы, также обозначаемые символами ⊥ и ⊤, соответственно), такие, что для Для всех элементов a , b и c из A верны следующие аксиомы
-
-
a ∨ ( b ∨ c ) = ( a ∨ b ) ∨ c a ∧ ( b ∧ c ) = ( a ∧ b ) ∧ c ассоциативность а ∨ б = б ∨ а а ∧ б = б ∧ а коммутативность а ∨ ( а ∧ б ) = а а ∧ ( а ∨ б ) = а поглощение а ∨ 0 = а а ∧ 1 = а личность a ∨ ( b ∧ c ) = ( a ∨ b ) ∧ ( a ∨ c ) a ∧ ( b ∨ c ) = ( a ∧ b ) ∨ ( a ∧ c ) распределенность а ∨ ¬ а = 1 а ∧ ¬ а = 0 дополняет
-
Обратите внимание, однако, что закон поглощения и даже закон ассоциативности могут быть исключены из набора аксиом, поскольку они могут быть выведены из других аксиом (см. ).. Булева алгебра, содержащая только один элемент, называется тривиальной булевой алгеброй или вырожденной булевой алгеброй
(В более старых работах некоторые авторы требовали, чтобы 0 и 1 были отдельными элементами, чтобы исключить этот случай.)
Булева алгебра, содержащая только один элемент, называется тривиальной булевой алгеброй или вырожденной булевой алгеброй . (В более старых работах некоторые авторы требовали, чтобы 0 и 1 были отдельными элементами, чтобы исключить этот случай.)
Из трех последних пар аксиом выше (тождество, дистрибутивность и дополнения) или из аксиомы поглощения следует, что
-
- a = b ∧ a тогда и только тогда, когда a ∨ b = b .
Отношение ≤, определяемое как a ≤ b, если эти эквивалентные условия выполняются, является частичным порядком с наименьшим элементом 0 и наибольшим элементом 1. Встреча a ∧ b и соединение a ∨ b двух элементов совпадают с их точной нижней гранью и супремумом соответственно, относительно ≤.
Первые четыре пары аксиом составляют определение ограниченной решетки .
Из первых пяти пар аксиом следует, что любое дополнение единственно.
Набор аксиом самодуален в том смысле, что если заменить ∨ на и 0 на 1 в аксиоме, результат снова станет аксиомой. Следовательно, применяя эту операцию к булевой алгебре (или булевой решетке), можно получить другую булеву алгебру с теми же элементами; это называется двойственным .
Логические функции
Логические функции одной переменной
| Функция | Название | Обозначение |
| Константа нуля | ||
| Повторение x | ||
| Логическое отрицание, инверсия, «НЕ» | ||
| Константа единицы |
| Переменная | Логические функции | |||
| x | ||||
| 1 | 1 | |||
| 1 | 1 | 1 |
Логические функции двух переменных
| Функция | Название | Обозначение |
| Константа нуля | или False | |
| Логическое умножение, конъюнкция, «И» | или или или | |
| Запрет по | или | |
| Переменная | ||
| Запрет по | или | |
| Переменная | ||
| Сложение по модулю 2, отрицание эквивалентности, исключающее «ИЛИ» | или или | |
| Логическое сложение, дизъюнкция, «ИЛИ» | или или или | |
| Функция Пирса (Вебба), «ИЛИ-НЕ» | или или | |
| Логическая равнозначность, эквиваленция | или или или | |
| Отрицание | ||
| Правая импликация | или | |
| Отрицание | ||
| Левая импликация | или | |
| Функция Шеффера, «И-НЕ» | или или | |
| Константа единицы | или True |
Ниже дана таблица истинности для логических функций от двух переменных.
| X1 | 1 | 1 | ||
| X2 | 1 | 1 | ||
| 1 | ||||
| 1 | ||||
| 1 | 1 | |||
| 1 | ||||
| 1 | 1 | |||
| 1 | 1 | |||
| 1 | 1 | 1 | ||
| 1 | ||||
| 1 | 1 | |||
| 1 | 1 | |||
| 1 | 1 | 1 | ||
| 1 | 1 | |||
| 1 | 1 | 1 | ||
| 1 | 1 | 1 | ||
| 1 | 1 | 1 | 1 |
В логических схемах функции могут быть реализованы с произвольных количеством
входных переменных, примеры — в материале Логические схемы и таблицы истинности.
Ответить на контрольные вопросы, а затем посмотреть ответы
Контрольный вопрос 1. Даны две переменные
и .
Число различных булевых векторов и различных ФАЛ от полученных векторов равны соответственно:
- 8 и 16
- 8 и 32
- 4 и 8
- 4 и 16
Контрольный вопрос 2. Какие из функций не являются ФАЛ одной переменной
(и одна, и вторая в варианте ответа):
- отрицание и сложение по модулю два
- эквивалентность и повторение
- отрицание и импликация
- функция Шеффера и эквивалентность
- запрет по и отрицание
Булева алгебра в финансах
Булева алгебра находит применение в финансах посредством математического моделирования рыночной деятельности. Например, исследованию цен на опционы на акции может помочь использование бинарного дерева для представления диапазона возможных результатов для базовой ценной бумаги. В этой биномиальной модели ценообразования опционов, где есть только два возможных результата, логическая переменная представляет увеличение или уменьшение цены ценной бумаги.
Этот тип моделирования необходим, потому что для американских опционов, которые могут быть исполнены в любое время, траектория цены ценной бумаги так же важна, как и ее окончательная цена. Модель ценообразования биномиальных опционов требует, чтобы траектория цены ценной бумаги была разбита на серию дискретных временных диапазонов.
Таким образом, модель ценообразования биномиальных опционов позволяет инвестору или трейдеру отслеживать изменение цены актива от одного периода к другому. Это позволяет им оценивать вариант на основе решений, принятых на разных этапах. Поскольку опцион в США может быть исполнен в любое время, это позволяет трейдеру определить, следует ли ему исполнять опцион или удерживать его в течение более длительного периода. Анализ биномиального дерева позволит трейдеру заранее увидеть, следует ли исполнять опцион. Если есть положительное значение, то опцион должен быть исполнен, если значение отрицательное, то трейдер должен удерживать позицию.
#Б
Аналитическое представление логических функций
В качестве исходного описания сложных логических функций обычно используется таблица истинности,
однако упрощение функций удобнее производить в аналитической форме. При аналитической записи функция алгебры логики
представляется либо в виде логической суммы элементарных логических произведений (дизъюнкции элементарных конъюнкций),
либо в виде логического произведения элементарных логических сумм (конъюнкции элементарных дизъюнкций). Первая форма
записи имеет название дизъюнктивной нормальной формы (ДНФ), вторая — конъюнктивной нормальной формы (КНФ). В этих
названиях термин «нормальная» означает отсутствие общей инверсии (отрицания) над несколькими перемнными сразу.
Дизъюнктивная нормальная форма
.
| X1 | X2 | f |
| 1 | ||
| 1 | 1 | |
| 1 | 1 | |
| 1 | 1 |
Конъюнктивная нормальная форма
.
| X1 | X2 | f |
| 1 | ||
| 1 | 1 | |
| 1 | 1 |
Что такое булева алгебра?
Булева алгебра – это раздел математики, который занимается операциями с логическими значениями и включает двоичные переменные. Булева алгебра берет свое начало в книге математика Джорджа Буля 1854 года.
Отличительной чертой булевой алгебры является то, что она занимается только изучением двоичных переменных. Чаще всего логические переменные представлены с возможными значениями 1 («истина») или 0 («ложь»). Переменные также могут иметь более сложные интерпретации, например, в теории множеств. Булева алгебра также известна как бинарная алгебра.
Ключевые выводы
- Булева алгебра – это раздел математики, который имеет дело с операциями над логическими значениями с двоичными переменными.
- Логические переменные представлены в виде двоичных чисел для представления истин: 1 = истина и 0 = ложь.
- Элементарная алгебра имеет дело с числовыми операциями, тогда как булева алгебра имеет дело с логистическими операциями.
- Булева алгебра использует соединение, дизъюнкцию и отрицание, в отличие от сложения, вычитания, умножения и деления.
- Основное современное использование булевой алгебры – это языки компьютерного программирования.
- В финансах в моделях ценообразования биномиальных опционов используется булева алгебра, которая помогает определить, когда опцион должен быть исполнен.
Способы описания логических функций
Применяются следующие способы описания логических функций:
- словесный;
- табличный;
- числовой;
- аналитический;
- координатный;
- графический.
Пример табличного описания функций алгебры логики. В верхней таблице
под набором подразумевается набор значений логических переменных (1 или 0), а f — это
значение функции алгебры логики, заданной определённой формулой. Нижняя таблица несёт в себе более
подробную информацию о наборах, поскольку в ней указаны значения переменных.
| Номер набора | f |
| 1 | 1 |
| 2 | |
| 3 | |
| 4 | 1 |
| 5 | 1 |
| 6 | |
| 7 | 1 |
| X1 | X2 | X3 | f |
| 1 | 1 | ||
| 1 | |||
| 1 | 1 | ||
| 1 | 1 | ||
| 1 | 1 | 1 | |
| 1 | 1 | ||
| 1 | 1 | 1 | 1 |
Приведённые выше таблицы имеют название таблиц истинности. Такие таблицы
в практике необходимо строить для любой, сколь либо сложной булевой функции. Примеры таблиц
истинности для булевых функций, реализованных в логических схемах — в материале
Логические схемы и таблицы истинности.
Пример числового описания логических функций
или .
Пример аналитического описания логических функций
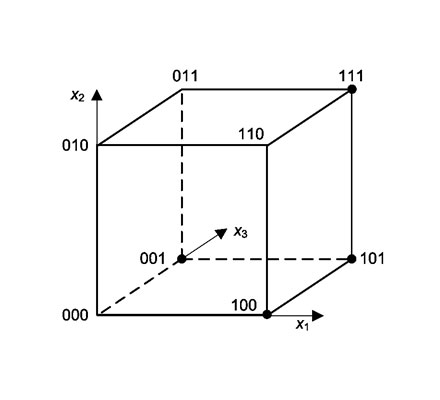
Пример координатного описания логических функций
Карта Карно
Пример графического описания логических функций