Автомат — миля
|
Взаимодействие управляющего автомата и операционного блока.| Схема выделения состояний управляющего автомата. |
Автомат Мили, построенный по микропрограмме, имеет чис-ло состояний, как правило, меньшее числа состояний эквива-лентного ему автомата Мура. С этой точки зрения использование автомата Мили предпочтительно. Однако применение автомата Мили в качестве управляющего автомата не всегда возможно. У автомата Мили переход в новое состояние осуществляется одновременно с формиро-ва Гем выходного сигнала. Поэтому, если ОБ вырабатывает оповещающие сигналы и… Мили, возможна следующая недопустимая ситуация: автомат Мили еще не сменил состояние, а на его входы пришли новые значения оповещающих сигналов, требующие выполнения иного перехода.
Автомат Мили, построенный по микропрограмме, имеет число состояний, как правило, меньшее числа состояний эквивалентного ему автомата Мура. С этой точки зрения использование автомата Мили предпочтительно. У автомата Мили переход в новое состояние осуществляется одновременно с формированием выходного сигнала. Мили, возможна следующая недопустимая ситуация: автомат Мили еще не сменил состояние, а на его входы пришли новые значения оповещающих сигналов, требующие выполнения иного перехода.
Автомат Мили имеет число состояний, меньшее, чем автомат Мура, однако его комбинационная схема может оказаться сложнее. При сравнении моделей необходимо также учитывать, что у автомата Мили выходной сигнал формируется одновременно с переходом автомата в новое состояние, что может затруднить сопряжение работы УА и ОА во времени.
Почему автомат Мили не всегда может использоваться в качестве управляющего автомата.
|
Микропрограммный автомат на элементах задержки. |
Поскольку автомат Мили имеет число состояний меньшее, чем число состояний эквивалентного ему автомата Мура, то путем построения автомата по схеме Мили может быть достигнута экономия в числе запоминающих элементов.
Пусть автомат Мили задан таблицей переходов и таблицей выходов ( табл. 3.5), где в клетках таблицы переходов записаны состояния, в которые переходит автомат из исходного состояния при соответствующем входе, а в клетках таблицы выходов записывается выход при тех же условиях. Нетрудно видеть, что приведенный пример соответствует реверсивному счетчику, причем выходы Y1 и Y2 соответствуют выдаче сигналов переноса.
Поэтому автоматы Мили и Мура обладают равными функциональными возможностями в том смысле, что всякое преобразование дискретной информации, осуществляемое в одном из них, осуществимо и в другом.
Для автомата Мили на каждом входном векторе надо проверять и выходные вектора и внутренние состояния, если они доступны.
|
Граф-автомата Мили а2 и отмеченные сигналами x2 / yz и. |
Граф автомата Мили определяется по отмеченному графу микропрограммы ( см. рис. 5.2) следующим образом. На рис. 5.3 проставляются вершины графа, соответствующие состояниям а, аъ а2, а3 автомата.
Два автомата Мили тогда и только тогда эквивалентны между собой ( в смысле совпадения индуцируемых ими автоматных отображений), когда эквивалентны их начальные состояния.
В автомате Мили с начальным состоянием а0 связана некоторая совокупность выходных сигналов, по которым выполняются соответствующие микрооперации. В связи с этим переходы в автомате Мура должны происходить в начале такта по поступлении запускающего сигнала Z. При необходимости граф автомата Мили может быть дополнен начальным состоянием ан. Окончанию операции соответствует переключение автомата в исходное состояние ан.
Закон функционирования автомата Мили может задаваться с использованием совмещенной таблицы переходов и выходов. В этом случае в клетках таблицы указываются значения функции переходов и функции выходов в виде AIY.
Программная реализация автомата Мура
Функции переходов и выходов можно представить таблицами, а реализовать их программно — с помощью ассоциативных массивов, индексы которых представляются символьными строками,
содержащими имена состояний и команд. Далее рассматривается, как это сделать.
Переходы состояний
var trans=; // массив переходов состояний автомата trans=; trans="левая"; trans="правая"; trans="зад"; trans=; trans="зад"; trans="анфас"; trans="правая"; trans=; trans="анфас"; trans="зад"; trans="левая"; trans=; trans="правая"; trans="левая"; trans="анфас";
Выходы состояний
src<img id=’myimg’ …>
var out=; // массив выходов автомата
out =function() {document.getElementById('myimg').src="front.jpg"}
out =function() {document.getElementById('myimg').src="left.jpg"}
out=function() {document.getElementById('myimg').src="right.jpg"}
out =function() {document.getElementById('myimg').src="back.jpg"}
Движок
automattransoutstatstatinput(команда)output()
function automat(trans,out,stat){ // движок автомата
this.trans=trans; // массив переходов
this.out=out; // массив выходов
this.stat=stat; // текущее состояние
this.input=function(inp){ // ввод команд
if (inp){
this.stat=this.trans;
this.output=out // выход
}
return this.stat
}
this.output=out;// выход
}
myautomat=new automat(trans,out,"анфас") // создание экземпляра объекта automat
myautomat.input("налево") // выдача команды
myautomat.output() // вычисление выхода
myautomat.input("налево");myautomat.input("налево");myautomat.input("налево");
myautomat.output()
<input type="button" value="направо"
onclick="myautomat.input(this.value);myautomat.output()"/>
<input type="button" value="налево"
onclick="myautomat.input(this.value);myautomat.output()"/>
<input type="button" value="кругом"
onclick="myautomat.input(this.value);myautomat.output()"/>
function automat(trans,out,stat){ // движок автомата
this.trans=trans; // массив переходов
this.out=out; // массив выходов
this.stat=stat; // текущее состояние
this.input=function(inp){ // ввод команд
if (inp){
this.stat=this.trans;
this.output=out // выход
this.output(); // вычисление выхода
}
return this.stat
}
this.output=out;// выход
this.output(); // вычисление выхода
}
Описание машины
Для заданного набора из шести детерминированных конечных автоматов с
(Q,Σ,Ω,δ,λ,q){\ displaystyle \ left (Q, \ Sigma, \ Omega, \ delta, \ lambda, q_ {0} \ right)}
Qзнак равно{q,q1,q2,q3}{\ Displaystyle Q = \ lbrace q_ {0}, \, q_ {1}, \, q_ {2}, \, q_ {3} \ rbrace},
Σзнак равно{Икс,y,z}{\ Displaystyle \ Sigma = \ lbrace х, \, y, \, z \ rbrace},
Ωзнак равно{а,б,c}{\ Displaystyle \ Omega = \ lbrace a, \, b, \, c \ rbrace}
и .
qзнак равноq{\ displaystyle q_ {0} = q_ {0}}
Функция перехода и функция вывода могут быть представлены графиком или таблицей станка .
δ{\ displaystyle \ delta}λ{\ displaystyle \ lambda}
|
||||||||||||||||||||||||||
| Представление графов и через графы δ{\ displaystyle \ delta}λ{\ displaystyle \ lambda} |
Изображение и машинная доска δ{\ displaystyle \ delta}λ{\ displaystyle \ lambda} |
Информация, подобная следующей, теперь может быть найдена как на графике, так и в таблице:
Если машина находится в состоянии и считывает оттуда символ «x» или символ «z», машина переходит в состояние . Когда статус достигнут, выводится «c».
q1{\ displaystyle q_ {1}}q3{\ displaystyle q_ {3}}q3{\ displaystyle q_ {3}}
Цифровая технология
Автомат Мура в цифровых технологиях
Машину Мура можно реализовать с помощью цифровых технологий. Для этого требуются две коммутационные сети и блок памяти с синхронизацией. В дополнение к логическим модулям, подключенным к печатной плате, реализация часто осуществляется с использованием программируемой логики и использования языка описания оборудования .
Обработка с помощью логических схем требует преобразования входного и выходного алфавита в двоичный код, аналогичный приведенной ниже таблице.
|
|
|
Что такое конечный автомат
конечное
Существуют несколько разновидностей конечного автомата. Здесь мы рассмотрим две из них — автомат Мура и автомат Мили.
В автомате Мура значения выходных параметров однозначно определяются состоянием, в котором он находится. При этом состояние, в которое он перейдет, однозначно определяется текущим состоянием и входной командой.
Точнее, конечный автомат Мура характеризуется следующими пятью элементами:
- С — конечное множество допустимых состояний;
- X — конечное множество допустимых входных сигналов (команд);
- Y — конечное множество допустимых выходных параметров (выходов);
- trans(c,x) — функция переходов состояний, однозначно сопоставляющая любым допустимым состоянию и команде некоторое допустимое состояние;
- out(c) — функция выходов, однозначно сопоставляющая любому допустимому состоянию некотрый допустимый выход.
начальное состояние
Функции переходов и выходов обычно представляют таблицами. При небольшом количестве состояний функцию переходов еще представляют в виде графа,
вершинам которого соответствуют состояния автомата, а направленным дугам, помеченным командами, — собственно переходы.
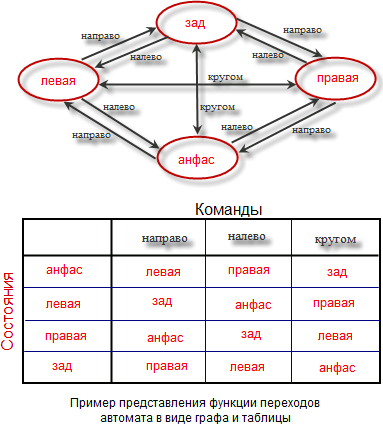
Автомат Мили отличается от автомата Мура только функцией выхода, которая определена на множестве всех пар состояние-команда. Точнее, out(c,x) определяет выход автомата,
который он будет иметь после подачи на него команды x, если при этом он находился в состоянии c. Любой конечный автомат Мили можно преобразовать в эквивалентный по поведению конечный автомат Мура,
и наоборот.
Формальное определение
Машина Мура — это кортеж из шести
- (Q,я,В,B,δ,λ){\ displaystyle (Q, я, A, B, \ delta, \ lambda)}
сделано из :
- конечный набор состояний ;Q{\ displaystyle Q}
- начальное состояние , элемент ;я{\ displaystyle i}Q{\ displaystyle Q}
- конечное множество , называется входной алфавит;В{\ displaystyle A}
- конечное множество , называется выходной алфавит;B{\ displaystyle B}
- переход функции ;δQ×В→Q{\ displaystyle \ delta: Q \ times от A \ до Q}
- выходная функция .λQ→B{\ displaystyle \ lambda: Q \ to B}
Состояние удобно отмечать с помощью, а символ вывода — с помощью . Функция перехода и функция вывода расширяются до слов по индукции, для и с помощью
δ(q,в){\ Displaystyle \ дельта (д, а)}q⋅в{\ displaystyle q \ cdot a}λ(q⋅в){\ Displaystyle \ лямбда (д \ CDOT а)}q⋆в{\ displaystyle q \ star a}В*{\ displaystyle A ^ {*}}ш∈В*{\ Displaystyle ш \ в А ^ {*}}в∈В{\ displaystyle a \ in A}
- q⋅швзнак равно(q⋅ш)⋅в,q⋆швзнак равно(q⋆ш)((q⋅ш)⋆в).{\ displaystyle q \ cdot wa = (q \ cdot w) \ cdot a, \ quad q \ star wa = (q \ star w) ((q \ cdot w) \ star a).}
Другими словами, вывод, производимый словом , прочитанным из состояния , является словом, произведенным словом , прочитанным из состояния , за которым следует буква, связанная с состоянием, достигнутым после чтения .
шв{\ displaystyle wa}q{\ displaystyle q}ш{\ displaystyle w}q{\ displaystyle q}q⋅шв{\ displaystyle q \ cdot wa}шв{\ displaystyle wa}
Функция , выполняемая с помощью автомата Мура является применение определяется по формуле:
жВ*→B*{\ displaystyle f: A ^ {*} \ to B ^ {*}}
- ж(ш)знак равноя⋆ш{\ Displaystyle F (ш) = я \ звезда ш}
Следовательно, это функция, которая со словом of , считываемым из начального состояния , связывает слово on, полученное путем конкатенации букв, связанных с состояниями прибытия пройденных переходов.
ш{\ displaystyle w}В*{\ displaystyle A ^ {*}}я{\ displaystyle i}B*{\ displaystyle B ^ {*}}
Варианты
Иногда машина Мура имеет конечный набор конечных состояний . Затем выполняемая функция ограничивается словами рационального языка во входном алфавите, распознаваемом автоматом. Тогда язык слов, производимых функцией, является рациональным языком .
ж{\ displaystyle f}ж{\ displaystyle f}
Обычно переходная функция является полной; когда он частичный, отсутствие перехода приводит к блокировке ПЛК.
δQ×В→Q{\ displaystyle \ delta: Q \ times от A \ до Q}
Проблема
В упомянутой статье Мур рассматривает машины типа ( n ; m ; p ). Это автоматы, имеющие n состояний, m входных символов и p выходных символов. В разделе « Дальнейшие задачи » в конце статьи он предлагает изучить следующую задачу: «Улучшение оценок, приведенных в теоремах 8 и 9». Теорема 8 выглядит следующим образом:
Теорема 8 — Для машины типа ( n ; m ; p ) такой, что любые два ее состояния различимы, существует эксперимент длины, который определяет состояние в конце эксперимента.
нет(нет-1)2{\ Displaystyle п (п-1) / 2}
Анатолий Алексевич Карацуба решил задачу Мура об усовершенствовании указанного терминала, доказав в 1957 году, когда он был студентом механического факультета МГУ им. М.В. Ломоносова , следующий результат:
Теорема — Учитывая машину типа ( п ; м ; р ) , так что любые два из его состояний различимы, есть длина эксперимент , который определяет состояние в конце эксперимента. Кроме того, этот предел достигнут.
(нет-1)(нет-2)2+1{\ Displaystyle (п-1) (п-2) / 2 + 1}
Этот результат был опубликован в 1960 году.
Реакция автоматов на входное слово[править]
Автомат Милиправить
Допустим, входное слово поступает на вход автомата буква за буквой.
Выходное слово называется реакцией автомата Мили на входное слово в состоянии строится по таблице переходов и выходов).
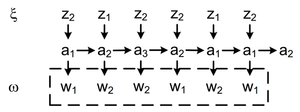
Реакцию автомата на входное слово можно заменить обходом графа.
Автомат Мураправить
Выходное слово называется реакцией автомата Мура на входное слово в состоянии .
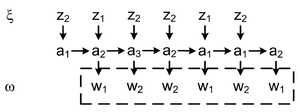
В рассматриваемом примере для автоматов Мили и Мура реакции автоматов на одинаковое входное слово совпадают, но они сдвинуты на один такт. Автоматы Мили и Мура дающие одинаковые реакции на одинаковые входные слова называются эквивалентными. Данное замечание приводит к задаче построения эквивалентных автоматов, дающих одинаковые реакции на одинаковые входные слова.