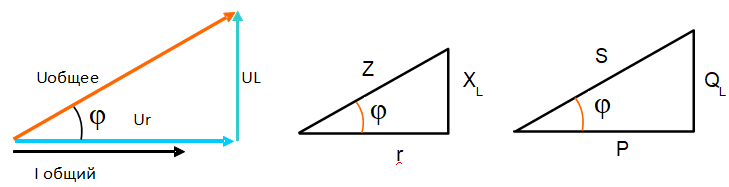Идеальный колебательный контур. формула томсона

Приставка к мультиметру esr метр

Я внес минимальные изменения. Корпус — от неисправного «электронного дросселя» для галогеновых ламп. Питание — батарея «Крона» 9 Вольт и стабилизатор 78L05 . Убрал переключатель — измерять LowESR в диапазоне до 200 Ом надо очень редко (если приспичит, использую параллельное подключение).

Изменил некоторые детали. Микросхема 74HC132N, транзисторы 2N7000 (to92) и IRLML2502 (sot23). Из-за увеличения напряжения с 3 до 5 Вольт отпала необходимость подбора транзисторов. При испытаниях устройство нормально работало при напряжении батареи свежей 9,6 В до полностью разряженной 6 В.

Кроме того, для удобства, использовал smd-резисторы. Все smd-элементы прекрасно паяются паяльником ЭПСН-25. Вместо последовательного соединения R6R7 я использовал параллельное соединение — так удобнее, на плате я предусмотрел подключение переменного резистора параллельно R6 для подстройки нуля, но оказалось, что «нуль» стабилен во всем диапазоне указанных мною напряжений.

Удивление вызвало то, что в конструкции «разработанной в журнале» перепутана полярность подключения VT1 — перепутаны сток и исток (поправьте, если я неправ). Знаю, что транзисторы будут работать и при таком включении, но для редакторов такие ошибки недопустимы.

↑ Наладка

Наладка очень проста и заключается в установке чувствительности с помощью R4 при подключенном резисторе 2…5 Ом и установке нуля цифрового вольтметра на диапазоне 200mV.

Операции надо повторить несколько раз, далее можно убедиться в точности измерителя, подключая резисторы 0,1…5 Ом.

Настраивать надо со штатными шнурами, плату хорошенько промыть, конденсатор С3 должен быть термостабилен.

↑ К вопросу о точности вообще

Начиная с 10 Ом, точность примерно 3% и ухудшается примерно до 6% при 20 Ом (200мВ), но точность при измерениях бракованных элементов не важна. Поскольку измерения проводятся при комнатной температуре, термонестабильность будет мала, испытаний на эту тему я не проводил.

При измерениях ESR конденсаторов в компьютерных блоках питания и на материнских платах, я пришел к выводу, что конденсаторы от 1000 мкФ с сопротивлением 0,5 Ом надо срочно выпаивать и отправлять в ведро, нормальное ESR 0,02…0,05 Ом.

Попутно обнаружил, что у исправных конденсаторов ESR очень сильно зависит от температуры, так у конденсатора 22 мкФ ESR уменьшалась от тепла пальцев на 10%. Это объясняет, почему некоторые фанатичные лампадные конструкторы специально делают подогрев конденсаторов в катодных цепях с помощью проволочных обогревателей.

По этой причине, а также по причине имеющегося сопротивления контактов считаю, что в измерения тысячных долей Ом нет особой необходимости.

↑ Итого

Данный прибор работает у меня около месяца, его показания при измерениях конденсаторов с ESR в единицы Ом совпадают с прибором по схеме Ludens. Он уже прошёл проверку в боевых условиях, когда у меня перестал включаться компьютер из-за емкостей в блоке питания, при этом не было явных следов «перегорания», а конденсаторы были не вздувшимися.

https://youtube.com/watch?v=Q6bBJLlXjTI

Точность показаний в диапазоне 0,01…0,1 Ом позволила отбраковать сомнительные и не выбрасывать старые выпаянные, но имеющие нормальную ёмкость и ESR конденсаторы. Прибор прост в изготовлении, детали доступны и дёшевы, толщина дорожек позволяет их рисовать даже спичкой. На мой взгляд, схема очень удачна и заслуживает повторения.

↑ Файлы

Здравствуй, читатель! Меня зовут Игорь, мне 45, я сибиряк и заядлый электронщик-любитель. Я придумал, создал и содержу этот замечательный сайт с 2006 года. Уже более 10 лет наш журнал существует только на мои средства.

— Спасибо за внимание!

Игорь Котов, главный редактор журнала «Датагор»

Оригинальная статья в журнале «Радио» № 8 за 2011 год: ▼ radio-8-2011-esr-meter.7z 13/08/16 ️ 1,09 Mb ⇣ 54

Здравствуй, читатель! Меня зовут Игорь, мне 45, я сибиряк и заядлый электронщик-любитель. Я придумал, создал и содержу этот замечательный сайт с 2006 года. Уже более 10 лет наш журнал существует только на мои средства.

— Спасибо за внимание!

Игорь Котов, главный редактор журнала «Датагор»

Не секрет, что наибольшее число отказов современной аппаратуры происходит по вине оксидных конденсаторов. Это не только обрыв, потеря емкости, короткое замыкание, но и дефект, выражающийся в увеличении активной составляющей конденсатора.

Устройство и характеристики конденсатора

Конструкция конденсатора представляет собой две токопроводящие пластины, разделённые диэлектриком. Если приложить к пластинам напряжение от источника постоянного тока, то ток короткое время будет протекать через конденсатор, и он зарядится. На его пластинах (обкладках) накопится напряжение, равное напряжению источника. Длительность протекания тока и ёмкость его заряда зависят от площади обкладок и расстояния между ними. Ёмкость обозначается буквой С и измеряется в фарадах. Единица измерения в системе СИ – 1Ф (F). Обозначение принято в честь физика из Англии М. Фарадея.

Внимание! Ёмкость 1Ф – очень большая величина. Если рассматривать Землю как уединённый проводник в форме шара, то ёмкость составила бы около 700 мкФ

Поэтому электротехнические элементы измеряют в малых величинах: пикофарадах (пФ), нанофарадах (нФ), микрофарадах (мкФ).

Единицы измерения ёмкости

В цепях постоянного и переменного тока ёмкостной элемент ведёт себя по-разному. Если постоянный ток конденсатор через себя не пропускает, то переменному току, проходящему через него, оказывает определённое сопротивление. Это ещё одна важная характеристика конденсатора – ёмкостное сопротивление RC.

Сопротивление из разряда реактивных сопротивлений, рассчитывается по формуле:

Rс =1/6,28*f*C,

где:

• Rc – емкостное сопротивление, Ом;
• 6,28 – 2 π;
• f – частота тока, Гц;
• C – емкость данного конденсатора, Ф.

Важно! Как видно из формулы, для токов разной частоты сопротивление одного и того же элемента меняется. Чем выше частота тока, тем ниже ёмкостное сопротивление конденсатора

Различают конденсаторы постоянной и переменной ёмкости. Вторые имеют конструкцию, в результате которой изменяется расстояние между пластинами.

По типу исполнения конденсаторы постоянной ёмкости бывают:

• полярные электролитические;
• однослойные и многослойные керамические;
• высоковольтные керамические;
• полиэстеровые;
• танталовые;
• полипропиленовые конденсаторы.

Конструкция зависит от порядкового разряда ёмкости элемента, применяемого материала для пластин и диэлектрика.

Емкость и энергия конденсатора

Важнейшей характеристикой является электрическая емкость конденсатора – физическая величина, которая определяется как отношение заряда конденсатора одного из проводников к разности потенциалов между проводниками. Емкость изменяется в Фарадах, но величина 1 Ф является довольно большой, поэтому чаще всего емкость конденсаторов измерятся в микрофарадах (мкФ), нанофарадах (нФ) и пикофарадах (пФ).

Помимо емкости конденсаторы характеризуются еще одним параметром, а именно величиной напряжения, которое может выдержать его диэлектрик. При слишком больших значениях напряжения электроны диэлектрика отрываются от атомов, и диэлектрик начинает проводить ток. Это явление называется пробоем конденсатора, и в результате обкладки оказываются замкнутыми друг с другом.

Собственно, характеристикой, которая часто используется при работе с конденсаторами является не напряжение пробоя, а рабочее напряжение – то есть величина напряжения, при которой конденсатор может работать неограниченно долгое время, и пробоя не произойдет.

Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные заряды, которые возникают на разных обкладках, равны по модулю и противоположны по знаку. Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (φ1 — φ2) между его обкладками. В таблице ниже приведем основные параметры конденсаторов.

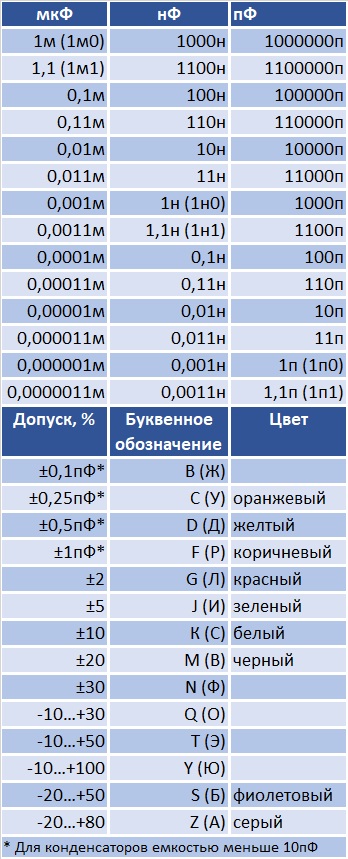
При небольших размерах конденсатор отличается значительной емкостью, не зависящей от наличия вблизи него других зарядов или проводников. Обкладкам конденсатора сообщают одинаковые по модулю, но противоположные по знаку заряды, что способствует накоплению зарядов, так как разноименные заряды притягиваются и поэтому располагаются на внутренних поверхностях пластин. Под зарядом конденсатора понимают заряд одной пластины.

https://youtube.com/watch?v=hvO47tPdMXM

Заряд и разряд

Процесс зарядки конденсатора не может быть мгновенным. Его время зависит от силы тока и электроёмкости. При подключении источника питания на одном проводнике собираются электроны, а на другом — остаются протоны. Так как между обкладками находится диэлектрик, то заряженные частицы не могут перейти на противоположную сторону. Но вместе с тем, электроны поступают от источника напряжения на пластины, поэтому ток в цепи всё же есть.

В начале периода зарядки разность потенциалов между обкладками равняется нулю. Как только на пластины переходят заряженные частицы, возникает напряжение. Происходит это из-за диэлектрика, который не даёт притягивающимся друг к другу зарядам перейти на другую сторону. В момент заряда конденсатора на его обкладках много свободного места. Электрический ток в этот момент не встречает сопротивления, и его величина достигает максимального значения. По мере разделения заряженных частиц сила тока снижается. Это происходит до тех пор, пока не исчезнет свободное место на обкладках конденсатора.

То время, которое проходит между начальным состоянием и полного заряда, называют переходным периодом заряда конденсатора. В его конце прекращается рост напряжения, и оно становится равным значению, выдаваемому источником питания. Если нарисовать зависимости тока и напряжения заряда от времени на графике, то можно будет увидеть, что их изменения проходят зеркально по отношению друг к другу.

Формула, по которой можно рассчитать, как происходит заряд конденсатора выглядит так: I = C * V / t, где:

• I — сила тока;
• С — ёмкость конденсатора;
• V / t — изменение напряжения за время.

Как только источник питания будет отключён, то вся энергия, запасённая конденсатором, будет отдана в нагрузку. Фактически устройство само на этом моменте превращается в источник питания. Электроны из-за силы притяжения существующей между разноимёнными частицами, начнут перемещаться в сторону положительно заряженной обкладки.

Но в тот момент, когда в цепи появится ток, конденсатор начнёт отдавать энергию, а напряжение на его выводах станет падать. Следовательно, сила тока тоже снизится. При этом время зарядки и разрядки конденсатора определяется двумя параметрами — ёмкостью и сопротивлением цепи.

Источник

Электрическая емкость плоского конденсатора

Электрическая емкость плоского конденсатора очень просто выражается через параметры его частей. Изменяя площадь пластин конденсатора и расстояние между ними легко убедиться, что электрическая емкость плоского конденсатора прямо пропорциональна площади его пластин (S) и обратно пропорциональна расстоянию между ними (d).

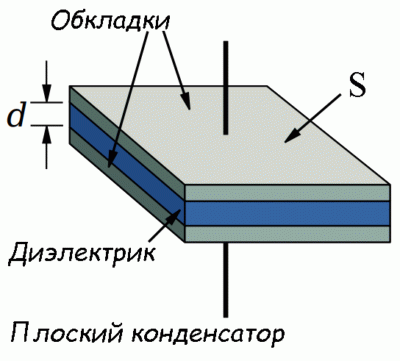
Емкость плоского конденсатора прямо пропорциональна площади его обкладок и диэлектрической проницаемости материала диэлектрика, разделяющего обкладки, и обратно пропорциональна расстоянию между ними:

C=εε0SdC=εε0Sd

Плоский конденсатор представляет из себя две плоские проводящие пластины, разделенные диэлектриком. Расстояние между пластинами много меньше характерного размера пластин. Поле вдали от краев пластин можно представить в виде суперпозиции полей бесконечно заряженных плоскостей.

Энергия заряженного конденсатора

Как и любая система заряжен­ных тел, конденсатор обладает энер­гией. Вычислить энергию заряжен­ного плоского конденсатора с одно­родным полем внутри него не­сложно.

Энергия заряженного конденса­тора.Для того чтобы зарядить конденсатор, нужно совершить рабо­ту по разделению положительных и отрицательных зарядов. Согласно закону сохранения энергии эта ра­бота равна энергии конденсатора.

В том, что заряженный конденсатор обладает энергией, можно убедиться, если разрядить его через цепь, со­держащую лампу накаливания, рас­считанную на напряжение в не­сколько вольт (рис.4). При раз­рядке конденсатора лампа вспыхи­вает.

Энергия конденсатора пре­вращается в другие формы: тепло­вую, световую.

Выведем формулу для энергии плоского конденсатора.

Напряженность поля, созданного зарядом одной из пластин, равна Е/2, где Е — напряженность поля в конденсаторе. В однородном поле одной пластины находится заряд q, распределенный по поверхности дру­гой пластины (рис.5). Согласно формуле Wp=qEd. для потенциальной энергии заряда в однородном поле энергия конденсатора равна:

(1)

где q — заряд конденсатора, a d — расстояние между пластинами.

(2)

Так как Ed=U, где U — разность потенциалов между обкладка­ми конденсатора, то его энергия равна:

Эта энергия равна работе, ко­торую совершит электрическое поле при сближении пластин вплот­ную.

Заменив в формуле (2) раз­ность потенциалов или заряд с по­мощью выражения для элек­троемкости конденсатора, получим

(3)

Можно доказать, что эти форму­лы справедливы для энергии любого конденсатора, а не только для плос­кого.

Энергия электрического поля.Согласно теории близкодействия вся энергия взаимодействия заряженных тел сконцентрирована в электриче­ском поле этих тел. Значит, энергия может быть выражена через основную характеристику поля — напря­женность.

Совет

Так как напряженность электри­ческого поля прямо пропорциональ­на разности потенциалов

(U = Ed),то согласно формуле

(4)

энергия конденсатора прямо пропор­циональна напряженности электри­ческого поля внутри него: Wp~E2. Детальный расчет дает следующее значение для энергии поля, приходя­щейся на единицу объема, т.е. для плотности энергии:

где ε0 — электрическая постоянная

Постоянный ток. Сила и плотность тока. Закон Ома.

Постоянный электрический ток

Краткие теоретические сведения

1. Сила тока определяется по формуле

Для постоянного тока

где – заряд, прошедшей через поперечное сечение проводника за время .

2.Если ток постоянный, плотность тока во всем сечении однородного проводника не изменяется ,

где – площадь поперечного сечения проводника.

Закон Ома

для однородного участка цепи имеет вид:

где – разность потенциалов (напряжение) на концах участка; – сопротивление.

Для неоднородного участка цепи этот закон записывается так:

где – ЭДС источника тока на этом участке; – внутреннее сопротивление источника;

– внешнее сопротивление цепи; – падение напряжения на участке 1-2.

· Для замкнутой цепи .

4.Сопротивление цилиндрического однородного проводника равно ,

где – удельное сопротивление; – удельная проводимость;

– длина; S – площадь поперечного сечения проводника.

Вектор магнитной индукции.

Вектор магнитной индукции – аналог напряженности электрического поля. Основной силовой характеристикой маг­нитного поля является вектор магнитной индукции.Вектор индукции магнитного поля B⃗направлен от южного полюса S стрелки (свободно вращающейся в магнитном поле) к северному N

Закон Ампера.

Закон Ампера – сила, действующая на проводник с током, помещенный в однородное магнитное поле, пропорциональна длине проводника, вектору магнитной индукции, силе тока и синусу угла между вектором магнитной индукции и проводником.

Магнитный момент витка с током – физическая величина характеризующий магнитные свойства системы в виде кругового витка с током Где, I ток протекающий по витку S площадь витка с током n нормаль к плоскости в которой находится виток

Задачи на конденсаторы и электроемкость с решением

Если вы не знаете, как решать задачи с конденсаторами, сначала посмотрите теорию и вспомните про памятку по решению задач по физике и полезные формулы.

Задача №1 на электроемкость батареи конденсаторов

Условие

Плоский конденсатор емкостью 16 мкФ разрезают на 4 равные части вдоль плоскостей, перпендикулярных обкладкам. Полученные конденсаторы соединяют последовательно. Чему равна емкость батaреи конденсаторов?

Решение

Из условия следует, что площадь получившихся конденсаторов в 4 раза меньше, чем у исходного. Зная это, можно найти емкость каждого полученного конденсатора:

Соединяя 4 таких конденсатора последовательно, получаем:

Ответ: 1 мкФ.

Задача №2 на энергию плоского конденсатора

Условие

Плоский конденсатор заполнили диэлектриком с диэлектрической проницаемостью, равной 2. Энергия конденсатора без диэлектрика равна 20 мкДж. Чему равна энергия конденсатора после заполнения диэлектриком? Считать, что источник питания отключен от конденсатора.

Решение

Энергия конденсатора до заполнения диэлектриком равна:

После заполнения емкость конденсатора изменится:

Энергия конденсатора после заполнения:

Ответ: 40 мкФ.

Задача №3 на последовательное и параллельное соединение конденсаторов

Условие

На рисунке изображена батарея конденсаторов. Каждый конденсатор имеет емкость 1 мкФ. Найдите емкость батареи.

Решение

Как видим, часть конденсаторов соединена параллельно, а часть последовательно. Это типичный пример смешанного соединения конденсаторов. Алгоритм решения задач при смешанном соединении конденсаторов сводится к тому, чтобы упростить схему и свести все только к параллельному или последовательному соединению.

Конденсаторы 3 и 4 соединены параллельно. Складывая их емкость, получаем в итоге последовательное соединение четырех конденсаторов: 1, 2, 5 и 3-4. Для параллельного соединения:

Для последовательного соединения:

Ответ: 0,285 мкФ.

Задача №4 на пролет частицы в конденсаторе

Заряд конденсатора равен 0,3 нКл, а емкость – 10 пФ. Какую скорость приобретет электрон, пролетая в конденсаторе от одной пластины к другой. Начальная скорость электрона равна нулю. 

Решение

По закону сохранения энергии, разность кинетических энергий электрона в начале и в конце пути будет равна работе поля по его перемещению. По условию, начальная кинетическая энергия электрона равна 0. Запишем:

С учетом этого, получим:

Ответ: 10^7 м/с.

Задача №5 на вычисление энергии электрического поля конденсатора

Условие

Конденсатор подключен к источнику постоянного напряжения U=1 кВ. Емкость конденсатора равна 5 пФ. Как изменяться заряд на обкладках конденсатора и его энергия, если расстояние между обкладками уменьшить в три раза.

Решение

Заряд конденсатора равен:

Изменение заряда будет равно:

Изменение энергии:

Ответ: 5 мкДж.

Конденсаторы

Для практического использования электрической энергии необходимо уметь ее накапливать. Для этого используют специальные устройства — конденсаторы.

Конденсаторы — это устройства, которые состоят из двух или более проводников, разделенных тонким слоем диэлектрика.

Проводники, из которых состоит конденсатор, называются обкладками

Как правило, при зарядке конденсатора заряды его обкладок равны по величине и противоположны по знаку. Под зарядом конденсатора

понимают значение заряда положительно заряженной обкладки.

Термин «конденсатор » от латинского слова condensare — сгущать ввел А.Вольта (итальянский физик) в 1782 г. Первые электрические конденсаторы были изготовлены Э.Клейстом и П. Ван Мушенбреком в 1745 г. По имени города Лейдена, где работал Мушенбрек, французкий физик Жан Нолле назвал их лейденскими банками.

При небольших размерах конденсатор отличается значительной емкостью, не зависящей от наличия вблизи него других зарядов или проводников.

Электроемкостью конденсатора называют физическую величину, численно равную отношению заряда конденсатора к разности потенциалов между его обкладками:

\(~C = \dfrac{q}{\varphi_1 — \varphi_2}\) или \(~C = \dfrac qU .\)

Из этой формулы видно, что чем больше напряжение между обкладками конденсатора, тем больше на них заряд. Но для каждого конденсатора существует предельное (максимальное)напряжение , выше которого диэлектрик начнет разрушаться. При этом заряды обкладок конденсатора мгновенно нейтрализуются, происходитпробой , т.е. конденсатор выходит из строя.

Виды конденсаторов

Конденсаторы можно классифицировать по следующим признакам и свойствам:

• по форме обкладок различают конденсаторы плоские, сферические, цилиндрические и др.;
• по типу диэлектрика (рис. 1) —бумажные (а), воздушные (б), слюдяные, керамические, электролитические (в) и т.д.;
• по рабочему напряжению — низковольтные (напряжение пробоя до 100 В) и высоковольтные (выше 100 В);
• по возможности изменения своей емкости — постоянной емкости (см. рис. 1, а, в), переменной емкости (см. рис. 1, б), подстроечные (рис. 2).

• а
• б
• в

Рис. 1

• Рис. 2
• Рис. 3

Другие виды конденсаторов показаны на рисунке 3.

См. так же Wikipedia Классификация конденсаторов

Электроемкость плоского конденсатора C

зависит от площади обкладокS , расстояния между нимиd и диэлектрической проницаемости диэлектрика ε, заполняющего пространство между обкладками конденсатора, но не зависит от материала, из которого эти пластины изготовлены \(~C = \dfrac{\varepsilon_0 \cdot \varepsilon \cdot S}{d},\) где ε0 — электрическая постоянная.

*Вывод формулы

Поле плоского конденсатора можно рассматривать как совокупность полей двух бесконечных разноименно заряженных плоскостей (рис. 2, а и б). Напряженность поля (рис. 2, в) можно найти по принципу суперпозиции:

\(\vec{E}=\vec{E}_{1} +\vec{E}_{2},\)

где \( E_{1} = E_{2} =\dfrac{\sigma }{2\varepsilon _{0} \cdot \varepsilon } =\dfrac{q}{2\varepsilon _{0} \cdot \varepsilon \cdot S}\) — напряженности электрических полей каждой из обкладок конденсатора, σ

— поверхностная плотность заряда на обкладках конденсатора. Тогда в проекциях на ось 0Х:

справа и слева от пластин — \(E_х = 0\);

между пластин — \(E=2E_{1} =\dfrac{q}{\varepsilon _{0} \cdot \varepsilon \cdot S}.\)

• а
• б
• в

Рис. 4 Электроемкость плоского конденсатора \(~C = \dfrac qU\), где \(U = E \cdot d,\) d

— расстояние между пластин. Следовательно, \(C =\dfrac{q}{E\cdot d} = \dfrac{q}{d} \cdot \dfrac{1}{E} = \dfrac{q}{d} \cdot \dfrac{\varepsilon _{0} \cdot \varepsilon \cdot S}{q} = \dfrac{\varepsilon _{0} \cdot \varepsilon \cdot S}{d}.\).

• При быстром разряде конденсатора можно получить импульс большой мощности, например, в фотовспышках, электромагнитных ускорителях, импульсных лазерах и т. п.
• Так как конденсатор способен длительное время сохранять заряд, то его можно использовать в качестве элемента памяти или устройства хранения электрической энергии.
• Емкость конденсатора заметно изменяется при малейших изменениях параметра конденсатора. Так малое изменение расстояния между обкладками учитывается в измерителях малых перемещений, изменение состава диэлектрика при изменении влажности фиксируется в измерителях влажности, учет изменения высоты диэлектрика между обкладками конденсатора позволяет измерять уровень жидкости и т.п.
• Конденсаторы (совместно с катушками индуктивности и/или резисторами) используются для построения различных цепей с частотно-зависимыми свойствами, в частности, фильтров, цепей обратной связи, колебательных контуров и т. п.

Для чего нужен

Эти устройства отличаются также широкой сферой применения. Вот лишь некоторые допустимые варианты:

1. Хранение аналоговых сигналов.
2. Сохранение цифровых данных.
3. Сфера телекоммуникационной связи. В этом случае главная функция — регулировка частоты, настройка профессионального оборудования.
4. Использование при создании различных источников питания.
5. Сглаживание выпрямленного напряжения на выходе устройств. Другой вопрос — в чём измеряется ёмкость конденсаторов.

Ещё одна возможная функция — генерация высокого напряжения, которое во много раз больше по сравнению с входными параметрами. Конденсаторы могут быть отличным хранилищем для электронов. Даже при отключении цепи от заряда энергия продолжает сохраняться внутри, на протяжении длительного времени.

Плоский конденсатор

Итак, простейший конденсатор представляет из себя две плоские проводящие пластины, расположенные параллельно друг другу и разделенные слоем диэлектрика. Причем расстояние между пластинами должно быть намного меньше, чем, собственно, размеры пластин. Такое устройство называется плоским конденсатором, а пластины – обкладками конденсатора.

Стоит уточнить, что здесь мы рассматриваем уже заряженный конденсатор (сам процесс зарядки мы изучим чуть позже), то есть на обкладках сосредоточен определенный заряд. Причем наибольший интерес представляет тот случай, когда заряды пластин конденсатора одинаковы по модулю и противоположны по знаку (как на рисунке).

А поскольку на обкладках сосредоточен заряд, между ними возникает электрическое поле, изображенное стрелками на нашей схеме. Поле плоского конденсатора, в основном, сосредоточено между пластинами, однако, в окружающем пространстве также возникает электрическое поле, которое называют полем рассеяния. Очень часто его влиянием в задачах пренебрегают, но забывать о нем не стоит. Для определения величины этого поля рассмотрим еще одно изображение плоского конденсатора:

Плоские конденсаторы

Каждая из обкладок конденсатора в отдельности создает электрическое поле:

• положительно заряженная пластина (+q) создает поле, напряженность которого равна
• отрицательно заряженная пластина (-q) создает поле, напряженность которого равна E_

Здесь – это поверхностная плотность заряда: . А – диэлектрическая проницаемость диэлектрика, расположенного между обкладками конденсатора. Поскольку площадь пластин конденсатора у нас одинаковая, как и величина заряда, то и модули напряженности электрического поля, равны между собой. Но направления векторов разные – внутри конденсатора вектора направлены в одну сторону, а вне – в противоположные. А какая же будет величина напряженности вне конденсатора? А все просто – слева и справа от обкладок поля пластин компенсируют друг друга и результирующая напряженность равна 0.

Электрическая ёмкость

Способность устройства накапливать заряд прежде всего зависит от его ёмкости. Найти её величину можно разделив заряд, сосредоточенный на пластинах, на разность потенциалов между ними: C = q / U. Полученный результат измеряется в фарадах . Так, ёмкость в 1 фарад будет равняться значению заряда в 1 кулон создавшему напряжение на выводах конденсатора 1 вольт. Кулон — это довольно большая величина. Поэтому на практике при различных расчётах приходится иметь дело с микрофарадами (µF), нанофарадами (nF) и пикофарадами (pF).

После создания «Лейденской банки» учёные провели ряд экспериментов, направленных на увеличение количества запасаемой энергии устройством. Так было обнаружено, что если между обкладками конденсатора поместить диэлектрик, то он не только предотвращает замыкание проводников, но и влияет на ёмкость.

Пусть имеется устройство пластины которого имеют площадь S. Между обкладками размещён непроводник тока, характеризующийся диэлектрической проницаемостью ε. Это коэффициент, показывающий во сколько раз напряжённость в однородном поле меньше чем создаваемое значение теми же зарядами в вакууме.

Можно предположить, что положительный заряд будет скапливаться на левой пластине, а отрицательный на правой. Чтобы найти ёмкость конденсатора нужно воспользоваться следующей последовательностью действий:

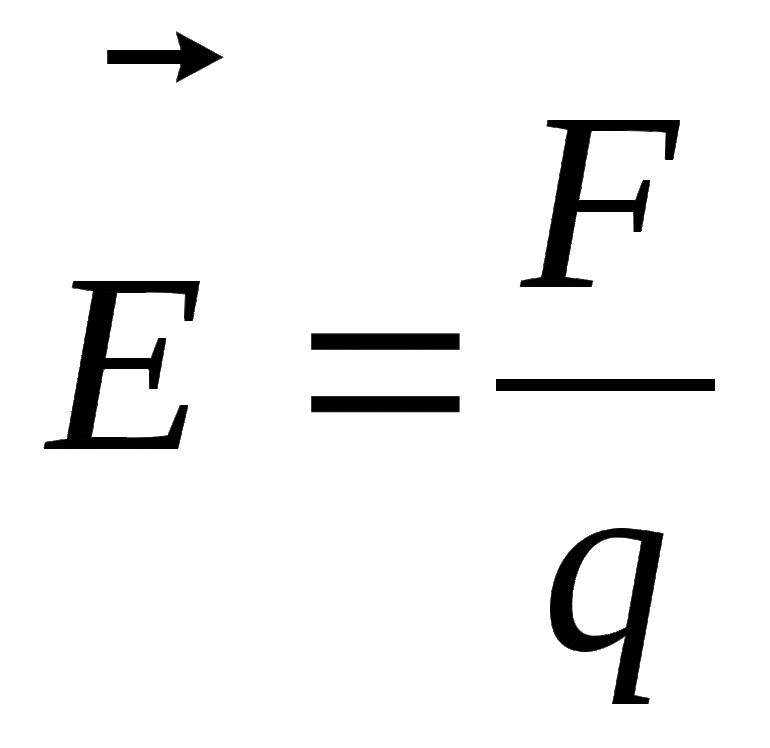
• Найти напряжённость поля в середине устройства. Для этого каждую обкладку нужно представить, как бесконечно однородно заряженную плоскость. Тогда: E1 = σ / (2 * ε * ε0). Так как поля внутри складываются, то расчётная формула примет вид: E = σ / (ε * ε0).
• Определить поверхностную плотность зарядов. Это величина, показывающая чему равняется отношение заряда к площади, по которой он распределён: σ = q / S.
• Выразить напряжение между пластинами через заряд. Между обкладками поле однородное. Значит, напряжение можно найти умножением напряжённости на расстояние: U = E * d. Тогда, пользуясь полученными формулами для E и σ, можно записать: U = (q * d) / (ε * ε0 * S).
• Вычислить электрическую ёмкость, подставив выражения в формулу: C = q / U. В результате получится: C = (ε * ε0 * S) / d.

Энергия поля плоского конденсатора

Как подобрать конденсатор

Для упрощения можно рассмотреть пример с перемещением разноименно заряженных пластин. Сформированная сила притяжения (F) будет измеряться величиной заряда (q) и напряженностью поля (E) между соответствующими обкладками:

F = q * E.

Так как E = q/(2*e*S), несложно получить выражение для значения силового взаимодействия:

F = q2/(2*e0*S),

где:

• e0 – это электрическая постоянная = 8,854 * 10-12 Ф*м-1;
• S – площадь пластин.

Работа (A) равна произведению силы на пройденное расстояние (d), поэтому W (энергия плоского конденсатора) = A = F * d = d *q2/(2*e0*S). Емкость (С) определяется, как C = d /(e0*S). Следующими преобразованиями можно получить итоговое выражение:

• W = q2/(2*C);
• q = C * U;
• энергия конденсатора формула:

W = ½ *C * U2.

Плоский конденсатор

Итак, простейший конденсатор представляет из себя две плоские проводящие пластины, расположенные параллельно друг другу и разделенные слоем диэлектрика. Причем расстояние между пластинами должно быть намного меньше, чем, собственно, размеры пластин. Такое устройство называется плоским конденсатором, а пластины – обкладками конденсатора.

Стоит уточнить, что здесь мы рассматриваем уже заряженный конденсатор (сам процесс зарядки мы изучим чуть позже), то есть на обкладках сосредоточен определенный заряд. Причем наибольший интерес представляет тот случай, когда заряды пластин конденсатора одинаковы по модулю и противоположны по знаку (как на рисунке).

А поскольку на обкладках сосредоточен заряд, между ними возникает электрическое поле, изображенное стрелками на нашей схеме. Поле плоского конденсатора, в основном, сосредоточено между пластинами, однако, в окружающем пространстве также возникает электрическое поле, которое называют полем рассеяния. Очень часто его влиянием в задачах пренебрегают, но забывать о нем не стоит. Для определения величины этого поля рассмотрим еще одно изображение плоского конденсатора:

Плоские конденсаторы

Каждая из обкладок конденсатора в отдельности создает электрическое поле:

• положительно заряженная пластина (+q) создает поле, напряженность которого равна
• отрицательно заряженная пластина (-q) создает поле, напряженность которого равна E_

Здесь – это поверхностная плотность заряда: . А – диэлектрическая проницаемость диэлектрика, расположенного между обкладками конденсатора. Поскольку площадь пластин конденсатора у нас одинаковая, как и величина заряда, то и модули напряженности электрического поля, равны между собой. Но направления векторов разные – внутри конденсатора вектора направлены в одну сторону, а вне – в противоположные. А какая же будет величина напряженности вне конденсатора? А все просто – слева и справа от обкладок поля пластин компенсируют друг друга и результирующая напряженность равна 0.

Похожие записи:

Светодиодные прожекторы на 50 вт: обзор моделей и цены Расчет освещенности помещения со светодиодными светильниками Обозначения постоянного и переменного тока: ac и dc ток Диод шоттки Все о пайке микросхем Как устранить опасность от разбитой люминесцентной лампы