Характерные признаки для резонанса напряжения

«Поющий» камень

Недалеко от Баку, столицы Азербайджана, есть пустыня со знаменитым «поющим» камнем. Он настолько известен, что получил имя — «Каменный бубен». Эта удивительная глыба имеет свойство: если ударить по ней камнем, то звук получается такой же громкий и чистый, как у колокола. Как же физика объясняет этот пример звукового резонанса?

Удар приводит к краткосрочной деформации — тут же от точки столкновения во все стороны бегут звуковые волны. На скорость их расхождения размеры камня не влияют. Однако волна может свободно распространяться только в неограниченном пространстве. А ведь мы знаем, что камень и воздух имеют границы (там, где они соприкасаются). Когда волна добегает до рубежа, она частично проходит в другую среду — из камня в воздух. Оставшаяся часть акустической энергии отражается в обратном направлении.

Резонанс в распределённых колебательных системах, нелинейные процессы

Разделение автоматических выключателей по время токовым характеристикам

Общим понятием для всех явлений данной категории можно назвать действенную связь с окружающей средой. В механических системах влияние на амплитуду фазовых характеристик процесса оказывает определенное положение в пространстве. В колебательном контуре радиоприемника, кроме собственного затухания, приходится учитывать реальный электромагнитный фон. При определенных условиях с высоким значением добротности допустимо образование стоячих волн.

Если пружина создана с различным распределением плотности витков, типовые формулы не действуют. Стандартные расчеты подразумевают равномерные упругость и деформации каждой части. Для уточнения нелинейности применяют корректирующие коэффициенты, сложные многоэтапные схемы вычислений.

Аналогичные особенности учитывают при использовании диодов или других радиотехнических компонентов с переменными амплитудно-частотными характеристиками. Если катушку индуктивности намотать на сердечнике из ферромагнитного материала, также придется учитывать нелинейность выходных параметров. Ее не получится описать элементарным уравнением закона Ома.

В нелинейных контурах при определенном спектральном распределении внешних воздействий присутствуют гармонические колебания. Кроме совпадения частот, значение имеет их амплитуда. В зависимости от настроек, они способны выполнять полезные и вредные функции. Определенные условия вызывают искажение формы базового сигнала.

Последовательное соединение

Катушка индуктивности и последовательно включенный в цепь конденсатор вместе особенным образом воздействуют на генератор, от которого запитана цепь. Также они влияют на фазовые соотношения напряжения и тока:

Первый элемент сдвигает фазу, при этом напряжение начинает обгонять ток примерно на четверть периода.
Второй элемент действует иначе. Он заставляет ток обгонять напряжение также на одну четвертую часть периода фазы.

Индуктивное сопротивление действует на смещение фаз, из-за чего его можно считать противоположным работе емкостного сопротивления. В результате итоговый сдвиг фаз между напряжением и током в цепи зависит от суммарного действия индуктивного и емкостного сопротивлений, а также соотношения между ними. От этого тоже зависит характер цепи.

Общее реактивное сопротивление определить просто. Необходимо сложить два показателя сопротивления:

Индуктивное от катушки.
Емкостное от конденсатора.

Из-за того, что они оказывают противоположное воздействие, одному из них присваивается отрицательный знак (обычно ёмкостному сопротивлению конденсатора). Тогда общее реактивное сопротивление можно найти так: из показателя катушки вычесть конденсатор. Если общее напряжение разделить на найденный параметр, то по закону Ома получится сила тока. Эту формулу можно легко изменить, переведя на напряжение. Оно будет равно произведению силы тока и разности двух сопротивлений (индуктивное берется с катушки, а емкостное — с конденсатора).

Если раскрыть скобку, то первое значение отразит действительный показатель части общего напряжения, которая старается преодолеть сопротивление. Второе — слагающая всего напряжения, которая пытается преодолеть емкостный параметр. Так, общее напряжение можно рассматривать как сумму этих слагаемых.

https://youtube.com/watch?v=KB0eMQ8loy0

Для определения этого значения нужно вычислить квадратный корень из суммы двух частей:

Общее активное сопротивление, возведенное в квадрат.
Квадрат разности индуктивного и емкостного сопротивлений, то есть общее реактивное.

https://youtube.com/watch?v=vp-uTZ_0FrQ

Электроника

В электрических цепях резонансом называется такой режим пассивной цепи, содержащий катушки индуктивности и конденсаторы, при котором ее входное реактивное сопротивление или ее входная реактивная проводимость равны нулю. При резонансе ток на входе цепи, если он отличен от нуля, совпадает по фазе с напряжением.

В электрических цепях резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.

Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником.

Электрическое устройство, состоящее из ёмкости и индуктивности, называется колебательным контуром. Элементы колебательного контура могут быть включены как последовательно (тогда возникает резонанс напряжений), так и параллельно (резонанс токов). При достижении резонанса, импеданс последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален. Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. В то же время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов.

Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения

ωL=1ωC⇒ω=1LC{\displaystyle \omega L={\frac {1}{\omega C}}\Rightarrow \omega ={\frac {1}{\sqrt {LC}}}},

где ω=2πf{\displaystyle \omega =2\pi f} ; f — резонансная частота в герцах; L — индуктивность в генри; C — ёмкость в фарадах

Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется добротностью системы.. В электронных устройствах также применяются различные электромеханические резонансные системы.

В электронных устройствах также применяются различные электромеханические резонансные системы.

Подробнее по этой теме см. Кварцевый резонатор.
Подробнее по этой теме см. Электромеханический фильтр.

Колебания и частота

Процедура, связанная с изменением положения системы рядом с точкой равновесного состояния и повторяющаяся с течением времени, называется колебаниями. Качающийся маятник повторяет свои движения относительно нормали к горизонтальной плоскости. При этом, если не прикладывать к его движению дополнительной энергии, его раскачивания затухнут.

Явление таких изменений можно классифицировать по следующим параметрам:

по математической модели, используемой в колебаниях;
по структуре периодичности;
по природе физических свойств;
по виду взаимодействия с окружающими условиями.

Внимание! Все колебания, независимо от своих физических свойств, имеют общие законы, которые можно описать волновыми явлениями. Эти закономерности исследует теория волновых колебаний. Механические колебания связаны с трансформацией одной формы энергии в другую, волновые – с пространственным передвижением и распространением энергии

Механические колебания связаны с трансформацией одной формы энергии в другую, волновые – с пространственным передвижением и распространением энергии.

Общими параметрами для всех колебаний являются:

частота;
период;
амплитуда.

Частотой считают количество колебаний, совершаемых телом за единицу времени. Единица измерения – герц (Гц), графическое обозначение – f, ʋ. Частота может быть круговой – при периодичном движении точки по окружности, ещё её называют циклической:

ω = 2π*T, (рад/с).

Период (T) являет собой время целого (полного) колебания, во время которого можно зафиксировать повторение любой из характеристик состояния системы. Это значит, что она совершила полное колебание. Обозначение периода – Т, единица измерения – секунда (с).

Две величины T и f являются обратными, что следует из формул:

T = 1/f;
f = 1/T.

Наибольшее отклонение точки тела или любой величины системы от равновесного положения называется амплитудой колебаний и обозначается буквой A. Единицей измерения являются те величины, изменения которых рассматриваются. При механических отклонениях амплитуду измеряют в метрах (м), амплитуду переменного напряжения – в вольтах (В) и так далее.

Период и частота механических колебаний

При каких условиях возникает явление: основные условия

Резонанс электротоков и напряжений появляется в результате сохранения тождества реактивных характеристик сопротивляемости сети. Несмотря на это, в ней должна быть и активная характеристика хотя бы минимального значения. Частота же генератора питания соединения всегда должна совпадать с частотой резонанса контура индуктивно-емкостной сети.

Обратите внимание! Условие работы сопротивления активного типа в реальных действующих схемах выполняется практически всегда. Одна лишь реактивная характеристика емкости и индуктивности возможна только в изолированных и теоретических примерах. График и векторная диаграмма возникновения резонирования

График и векторная диаграмма возникновения резонирования

Во время резонанса дроссель и конденсатор обмениваются накопленной энергией. В теоретических примерах, когда происходит первое подключение электрогенератора (в качестве питательного источника), энергия копится в катушке индуктивности или конденсаторе. После выключения электрогенератора из сети возникают колебания незатухающего характера, возникшие в результате этого обмена.

При каких условиях возникает явление: основные условия

Вам это будет интересно Что такое фаза и нуль в электричестве

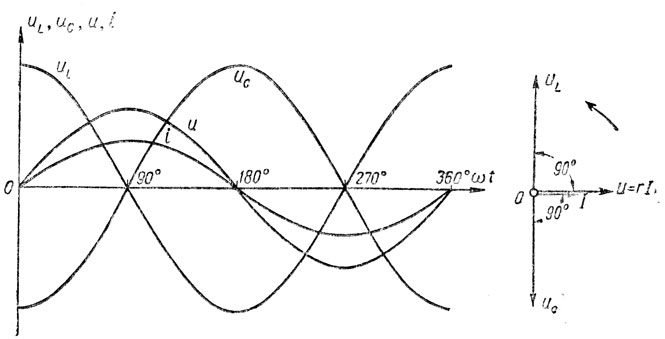
График и векторная диаграмма возникновения резонирования

Резонансные режимы работы электрических цепей

В электротехнике при анализе режимов работы электрических цепей широко используется понятие двухполюсника. Двухполюсникомпринято называть часть электрической цепи произвольной конфигурации, рассматриваемую относительно двух выделенных выводов (полюсов). Двухполюсники, не содержащие источников энергии, называются пассивными. Всякий пассивный двухполюсник характеризуется одной величиной – входным сопротивлением, т.е. сопротивлением, измеряемым (или вычисляемым) относительно двух выводов двухполюсника. Входное сопротивление и входная проводимость являются взаимно обратными величинами.

Пусть пассивный двухполюсник содержит одну или несколько индуктивностей и один или несколько конденсаторов. Под резонансным режимом работы такого двухполюсника понимают режим (режимы) двухполюсника при котором входное сопротивление является чисто активным. По отношению к внешней цепи двухполюсник ведет себя как активное сопротивление, вследствие чего входные напряжение и ток совпадают по фазе. Различают две разновидности резонансных режимов: резонанс напряжения и резонанс тока.

Резонанс напряжений

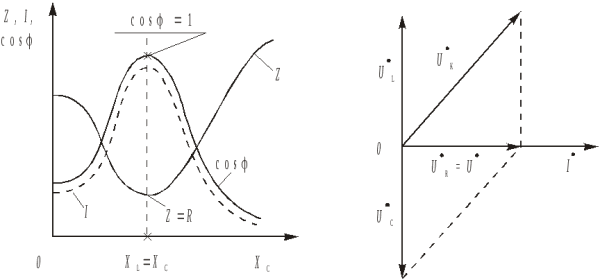
В простейшем случае резонанс напряжений может быть получен в электрической цепи переменного тока при последовательном включении катушки индуктивности и конденсаторов. При этом, изменяя емкость конденсаторов при постоянных параметрах катушки, получают резонанс напряжений при неизменных значениях напряжения и индуктивности, частоты и активного сопротивления цепи. При изменении емкости конденсаторов Спроисходит изменение реактивного емкостного сопротивления. При этом полное сопротивление цепи также изменяется, следовательно, изменяются ток, коэффициент мощности, напряжения на катушке индуктивности, конденсаторах, а также активная, реактивная и полная мощности электрической цепи. Зависимости токаI, коэффициента мощности cosи полного сопротивленияZцепи переменного тока в функции емкостного сопротивления (резонансные кривые) для рассматриваемой цепи приведены на рис. 9,а. Векторная диаграмма тока и напряжений этой цепи при резонансе представлена на рис. 9,б.

Как видно из этой диаграммы, реактивная составляющая напряжения U_Lна катушке при резонансе равна напряжениюU_Сна конденсаторе. При этом напряжение на катушке индуктивностиU_кпри резонансе вследствие того, что катушка кроме реактивного сопротивленияX_Lобладает еще и активным сопротивлениемR, несколько больше, чем напряжение на конденсаторе.

Анализ представленных выражений (2), а также рис. 9,аибпоказывают, что резонанс напряжений имеет ряд отличительных особенностей.

1. При резонансе напряжений полное сопротивление электрической цепи переменного тока принимает минимальное значение и оказывается равным ее активному сопротивлению, т.е.

2. Из этого следует, что при неизменном напряжении питающей сети (U= const) при резонансе напряжений ток в цепи достигает наибольшего значенияI =U/Z =U/R. Теоретически ток может достигать больших значений, определяемых напряжением сети и активным сопротивлением катушки.

а)б)

Рис. 9

3. Коэффициент мощности при резонансе cos=R/Z =R/R = 1, т.е. принимает наибольшее значение, которому соответствует угол= 0. Это означает, что вектор тока

_i_u

4. Активная мощность при резонансе P=RI2имеет наибольшее значение, равное полной мощностиS, в то же время реактивная мощность цепиQ=XI2= (X_LX_C)I2оказывается равной нулю:Q =Q_LQ_C= 0.

5. При резонансе напряжений напряжения на емкости и индуктивности оказываются равными U_С=U_L=X_CI =X_LIи в зависимости от тока и реактивных сопротивлений могут принимать большие значения, во много раз превышающие напряжение питающей сети. При этом напряжение на активном сопротивлении оказывается равным напряжению питающей сети, т.е.U_R=U.

Резонанс напряжений в промышленных электротехнических установках нежелательное и опасное явление, так как оно может привести к аварии вследствие недопустимого перегрева отдельных элементов электрической цепи или пробою изоляции обмоток электрических машин и аппаратов, изоляции кабелей и конденсаторов при возможном перенапряжении на отдельных участках цепи. В то же время резонанс напряжений широко используется в различного рода приборах и устройствах электроники.

StudFiles.ru

Примеры резонанса в жизни

Резонанс в электрической цепи

Рассмотренный выше пример – частный случай. Аналогичные проявления можно обнаружить в разных системах.

Борьба с блоком в дзюдо

Для эффектного броска опытный спортсмен умело повторяет раскачивающиеся движения противника. В определенный момент делает подсечку с толчком в нужном направлении. Грамотное сложение нескольких сил помогает выиграть поединок.

Журналисты утверждают, что Басков расколол бокал силой своего голоса

Для повышения рейтингов устаревающих певцов и анахронических средств массовой информации применяют разные технологии. Однако в самом принципе разрушения хрупкого изделия звуковым колебанием нет ничего удивительного. При широком голосовом диапазоне вполне допустимо совпадение частот. Профессиональный певец в состоянии обеспечить «генерацию» сильных колебаний даже без применения специализированного усилителя.

Разрушение стационарного моста в США (1940 год, штат Вашингтон)

В этом примере крепкую конструкцию уничтожил не многотонный грузовик или испытание атомной бомбы. Совпадение частот потока воздушных масс и моста провоцировало критическую нагрузку и показанные на фото результаты. Данный резонансный случай убедительно демонстрирует необходимость точного расчета для исключения аварийных и катастрофических ситуаций.

Виды и примеры резонанса

Только в самой физике различают такие виды резонанса как:

Механический резонанс – это все те же вышеупомянутые качели, резонанс моста от проходящей роты солдат, резонанс колокольного звона и т. д. Одним словом, резонанс, вызванный механическими воздействиями.
Акустический резонанс – это резонанс, благодаря которому работают все струнные музыкальные инструменты: гитара, скрипка, лютня, балалайка, банджо и т. д. К слову корпус музыкальных инструментов неспроста имеет свою форму. Звук, издаваемый струной при щипке, попадает внутрь корпуса и там вступает в резонанс со стенками, что в результате приводит к его усилению. По этой причине качество звучания той же гитары сильно зависит от того материала, из которого она сделана и даже от лака которым она покрыта.
Электрический резонанс – представляет собой совпадение частоты колебаний внешнего напряжения с частотой колебаний электрической цепи, по которой идет ток.

Помимо этих чисто физических резонансов есть еще уже упомянутый нами общественный резонанс – яркий отклик общества на какое-то событие (обычно политическое или экономическое), например брекзит Британии, ее выход из Европейского союза вызвал широкий общественный резонанс во многих странах Европы и особенно, разумеется, в самой Британии.

Есть также и когнитивный резонанс – это полное совпадение во взглядах и мнениях. Например, вы познакомились с новым человеком, а он думает так же как вы, у вас абсолютно схожие взгляды, вкусы, предпочтения, тогда имеет место когнитивный резонанс. И противоположное явление – когнитивный диссонанс, когда вы абсолютно не согласны с кем-то или чем-то, абсолютно не принимаете происходящего. (Например, автор этой статьи, оказавшись в каком-нибудь украинском бюрократическом учреждении, будь-то Жеке, БТИ или налоговой испытывает настоящий когнитивный диссонанс)).

Польза и вред резонанса

Изложенные сведения применяют для решения разных прикладных задач. Выяснив, что такое резонанс в физике, можно с помощью малых внешних сил развивать большую полезную мощность. Точный расчет предотвратит вредные воздействия, ухудшающие функциональное состояние механических аппаратов и электротехнических схем.

Положительный эффект

Изложенные принципы объясняют применение резонанса для обработки сигналов. Точный расчет компонентов и коэффициента связи контуров поможет создать эффективный фильтр, пропускающий электромагнитные колебания в определенном частотном диапазоне.

Последовательный контур можно использовать для повышения напряжения, если сеть питания неспособна поддерживать необходимый уровень. Правильно подобранный конденсатор обеспечит плавное включение привода, что продлит срок службы оборудования и снизит нагрузку на электростанцию.

К сведению. Хорошо известно применение резонанса в технике измельчения твердых горных пород. Аналогичный результат (ускорение процесса) получают при оснащении дрели ударно-возвратным механизмом.

Отрицательное воздействие

Резонанс разрушает прочные конструкции, функциональные узлы, механизмы. При ошибках в расчетах это явление ухудшает работоспособность электрических схем. Особо сильные воздействия провоцируют аварийные ситуации.

В качестве примера можно привести резонансные частоты, которые учитывают при создании санитарных, технических и производственных нормативов:

стоящий, сидящий и лежащий человек: 4-13 (16-26), 4-7 и 2,5-3 Гц, соответственно;
голова: 18-35 Гц;
грудная клетка: 2,5-4 Гц;
брюшная полость: 6-9 Гц.

При совпадении частоты вибраций (от инструмента, работающего оборудования) ухудшается состояние нервной системы, провоцируются паталогические изменения в организме.

Резонанс токов в параллельном колебательном контуре

Рассмотрим случай параллельного соединения колебательного контура с источником тока (рис. 1) и посмотрим, каково будет сопротивление контура для токов различных частот в этом случае. Если частота тока невелика (ниже резонансной), то почти весь ток пойдет по наиболее легкому для него пути — через индуктивную ветвь; сопротивление контура при низких частотах будет небольшим по величине и индуктивным по своему характеру.

Для токов высоких частот (выше резонансной) более легким путем будет путь через емкостную ветвь, и, следовательно, сопротивление контура будет также небольшим по величине, но емкостным по характеру.

При резонансной частоте, когда емкостное сопротивление равно индуктивному, путь для тока будет одинаково трудным через обе ветви. Мы знаем, что при параллельном соединении двух равных сопротивлений общее сопротивление равняется половине любого из них. Поэтому, казалось бы, что сопротивление контура при резонансе должно равняться половине одного из реактивных сопротивлений. Однако, не следует забывать, что мы имеет дело, с сопротивлениями, хотя и одинаковыми по величине, но имеющими принципиально различный характер. Это различие проявляется в том, что токи в индуктивной и емкостной ветвях контура сдвинуты по фазе друг относительно друга на 180°. Отсюда непосредственно следует, что в неразветвленной части цепи всегда протекает не суммарный, а разностный ток (рис. 1).

Рисунок 1. Токи при параллельном резонансе. В неразвлетвленной части цепи протекает не скммарный, а разностный ток.

Поэтому при резонансе, когда токи в емкостной и индуктивной ветвях равны между собой, ток в неразветвленной части цепи будет равен нулю, какое бы напряжение мы ни прилагали к контуру. При резонансе между точками АВ цепь будет казаться разорванной, т. е. сопротивление ее между этими точками будет бесконечно велико, а отнюдь не будет равным половине одного из реактивных сопротивлений. Практически бесконечно большого сопротивления контура при резонансе не бывает, так как из-за наличия активного сопротивления в контуре (сопротивление провода катушки) сдвиг фаз токов никогда не может быть равным точно 180°.

Однако активное сопротивление катушки обычно бывает много меньше ее индуктивного сопротивления, и поэтому сопротивление колебательного контура при резонансе может достигать очень больших величин.

Сопротивление колебательного контура при параллельном резонансе равно:

где L выражено в гн, С—в ф, RL—в ом.

Полное сопротивление колебательного контура при резонансе является чисто активным в силу того обстоятельства, что индуктивное и емкостное сопротивления взаимно компенсируются.

Кривые изменения полного сопротивления колебательного контура между точками АВ при изменении частоты тока приведены на рис. 2,б.

Рисунок 2. Резонанс токов. а) — схема и обозначения; б) — график полного сопротивления.

При параллельном резонансе токи ,в ветвях контура достигают наибольшей величины; поэтому параллельный резонанс называется резонансом токов.

Явление резонанса имеет огромнейшее значение в радиотехнике. На земном шаре имеется большое количество передающих радиостанций. Передачи всех этих радиостанций распространяются в эфипе и все одновременно принимаются приемной антенной. Нетрудно представить себе, каким получилось бы нагромождение друг на друга передач, если бы мы не могли выделить из этого хаоса только одну нужную нам. Вот тут-то на помощь приходит явление резонанса. Передающие радиостанции излучают в пространство электромагнитную энергию на различных частотах, мы же, настраивая контуры нашего приемника в резонанс с той или иной частотой, тем самым выбираем нужную нам передачу.

Резонанс напряжений

Если последовательно с генератором соединить конденсатор и катушку индуктивности, то, при условии равенства их реактивных сопротивлений, возникнет резонанс напряжений. При этом активная часть Z должно быть как можно меньшей.

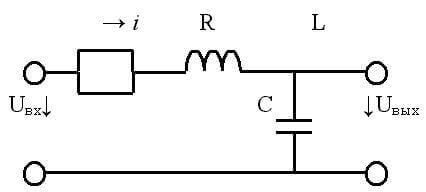
Стоит отметить, что индуктивность и емкость обладает только реактивными качествами лишь в идеализированных примерах. В реальных же цепях и элементах всегда присутствует активное сопротивление проводников, хоть оно и крайне мало.

При резонансе происходит обмен энергией между дросселем и конденсатором. В идеальных примерах при первоначальном подключении источника энергии (генератора) энергия накапливается в конденсаторе (или дросселе) и после его отключения происходят незатухающие колебания за счет этого обмена.

Напряжения на индуктивности и емкости примерно одинаковы, согласно закону Ома:

U=I/X

Где X — это Xc емкостное или XL индуктивное сопротивление соответственно.

Цепь, состоящую из индуктивности и емкости, называют колебательным контуром. Его частота вычисляется по формуле:

Период колебаний определяется по формуле Томпсона:

Так как реактивное сопротивление зависит от частоты, то сопротивление индуктивности с ростом частоты увеличивается, а у ёмкости падает. Когда сопротивления равны, то общее сопротивление сильно снижается, что отражено на графике:

Основными характеристиками контура являются добротность (Q) и частота. Если рассмотреть контур в качестве четырехполюсника, то его коэффициент передачи после несложных вычислений сводится к добротности:

K=Q

А напряжение на выводах цепи увеличивается пропорционально коэффициенту передачи (добротности) контура.

Uк=Uвх*Q

При резонансе напряжений, чем выше добротность, тем больше напряжение на элементах контура будет превышать напряжение подключенного генератора. Напряжение может повышаться в десятки и сотни раз. Это отображено на графике:

Потери мощности в контуре обусловлены только наличием активного сопротивления. Энергия из источника питания берется только для поддержания колебаний.

Коэффициент мощности будет равен:

cosФ=1

Эта формула показывает, что потери происходят за счет активной мощности:

S=P/Cosф

Чем может быть опасен резонанс напряжений

«Поющий» камень

Резонанс в распределённых колебательных системах, нелинейные процессы

Последовательное соединение

Электроника

Колебания и частота

При каких условиях возникает явление: основные условия

При каких условиях возникает явление: основные условия