Как возникает резонанс напряжения и токов: в чем опасность явления, как его можно использовать

Расчет цепей в резонансе и построение векторной диаграммы

Задачи, как обычно, принес студент. Они “родом” из нашего Ленинградского Политеха.

Задача 1. В цепи на рисунке В, А, А, Ом. В цепи резонанс. Определить: напряжения на всех ветвях, ток , напряжение , мощность . Построить векторную диаграмму.

Цепь к задаче 1

Решение.

По первому закону Кирхгофа (учитываем, что в цепи резонанс и токи в емкости и индуктивности находятся в противофазе, то есть на векторной диаграмме направлены в противоположные стороны)

Это абсолютное значение тока.

По закону Ома

Нам известно емкостное сопротивление – оно по условию равно 5 Ом. Поэтому, зная это сопротивление и ток в данной ветви, найдем напряжение на ней.

Так как индуктивность и емкость включены параллельно, то на индуктивности такое же напряжение – 50 В. Тогда по закону Ома индуктивное сопротивление

Теперь вернемся к напряжению . Это сумма двух напряжений – на емкости и на резисторе. Мы знаем, что напряжение на резисторе совпадает с током, а напряжение на емкости – нет. Его вектор будет перпендикулярен вектору тока и будет отставать от тока на . В то же время, поскольку цепь в резонансе, то напряжение на емкости должно быть скомпенсировано напряжением на индуктивности, а оно равно напряжению на емкости и опережает ток на . Изобразим все на векторной диаграмме (здесь ):

Векторная диаграмма

Из диаграммы понятно, что

Тогда

Определим мощность (активную), считая, что нам даны действующие значения токов.

Ответ: ток А, В, Вт, В.

Задача 2. В цепи на рисунке В, B, А, А. В цепи резонанс. Определить: напряжения на всех ветвях, ток , напряжение . Построить векторную диаграмму.

Схема к задаче 2

Решение.

Определим сразу напряжение на верхней ветви. Там протекает ток , и напряжение на резисторе с этим током совпадает, а вот напряжение на емкости должно отставать на . Поэтому, чтобы найти напряжение на обоих элементах, понадобится теорема Пифагора:

Понятно, что на второй ветви (с индуктивностью) такое же точно напряжение, потому что она включена параллельно.

Так как цепь в резонансе, то в итоге должно получиться так, что вектор тока и вектор напряжения (входное) совпадают по направлению на векторной диаграмме. При этом ток (в емкостной ветви) будет опережать это входное напряжение, а вот ток (в индуктивной) будет отставать от входного напряжения. И это опережение (и отставание тоже) будет на угол, меньший , так как сопротивление ветвей не чисто емкостное и не чисто индуктивное. При этом направление тока будет совпадать с направлением напряжения , а ток – с направлением напряжения .

Своим студентам я придумала подсказку:

«Каждый студент, запомни твердо!

От этого твой зависит зачет:

В емкости ток опережает,

А в индуктивности – отстает!»

Входное напряжение – это в данном случае и есть .

Чтобы дальше решать эту задачу, призовем векторную диаграмму на помощь. Построим сначала вектор тока и совпадающий с ним вектор напряжения , затем – отстающий на вектор напряжения . Сложим вектора обоих напряжений и получим вектор напряжения . Проведем ток , совпадающий с ним по направлению (резонанс).

Векторная диаграмма (не полная) – начало построения.

Таким образом, становится понятно, что, так как тангенс угла между напряжением и напряжением равен 2, то и между векторами токов точно такой же угол – потому что соотношение между их модулями тоже 2. Значит, вектор тока направлен вертикально вниз. Туда же должно быть направлено и напряжение , а вот напряжение на индуктивности должно опережать ток на – значит, оно совпадает с . Причем, оба последних вектора должны в сумме давать !

Векторная диаграмма к задаче 2

Значит, В, В. Таким образом, напряжение В (по второму закону Кирхгофа). Ток по теореме Пифагора

Можно воспользоваться законом Ома и определить Ом, Ом, Ом, Ом – вы можете это легко теперь сделать сами.

Ответ: А, В.

Использование резонанса напряжений для передачи радиосигнала

Колебательный контур этого типа создают из последовательной комбинации трех базовых компонентов: резистор, конденсатор, индуктивность. Подходящим для резонанса условием является нулевое сопротивление цепи (комплексное). Для решения такой задачи следует изучить основные формулы.

Комплексное сопротивление Rк=R+j(wL-1/wC). Постоянный резистор (R) не зависит от частоты (w). Значит, придется оперировать с индукционными и емкостными элементами. Резонансный эффект получают при (wL-1/wC)=0. Для вычисления необходимых значений пользуются следующими расчетами:

Lп=1/w2*C;
Сп=1/w2*L;
Wп=1/√L*C.

Из приведенных данных понятно, что корректировать можно любой из параметров при одновременном сохранении двух других. В практической схемотехнике удобнее работать с частотой, поэтому рассмотрим подробнее применение такого варианта.

Последовательный контур с графиками

На рисунках показаны условия возникновения резонанса напряжений. В точке, обозначенной w0, наблюдается равенство индуктивной и емкостной составляющих на определенной частоте. Небольшой сдвиг влево по оси обусловлен резистивным компонентом цепи.

Напряжение на конденсаторе (Uc) при частоте резонанса (W0) равно волновому сопротивлению колебательного контура (p=√L/C). Аналогичная разница потенциалов будет на клеммах катушки при частоте W0. Данная особенность объясняет особое название процесса – «резонанс напряжений». Также в электротехнических расчетах применяют следующие определения:

Добротность – Q=p/R;
Затухание – 1/Q.

Отмеченные свойства используют в радиоприемной и передающей аппаратуре. Выделение контуром определенного диапазона позволяет выполнять настройку станции на определенную частоту с определенной параметрами цепи погрешностью. Для контроля избирательности оценивают амплитуду сигнала относительно резонансной частоты. Уровень отклонения на 3 дБ в обе стороны (0,7 от максимума) называют полосой пропускания.

Амплитудно-частотная характеристика (АЧХ) и полоса пропускания

Реактивные сопротивления индуктивности и емкости

Индуктивностью называется способность тела накапливать энергию в магнитном поле. Для нее характерно отставание тока от напряжения по фазе. Характерные индуктивные элементы — дросселя, катушки, трансформаторы, электродвигатели.

Емкостью называются элементы, которые накапливают энергию с помощью электрического поля. Для емкостных элементов характерно отставание по фазе напряжения от тока. Емкостные элементы: конденсаторы, варикапы.

Приведены их основные свойства, нюансы в пределах этой статьи во внимание не берутся. Кроме перечисленных элементов другие также имеют определенную индуктивность и емкость, например в электрических кабелях распределенные по его длине

Кроме перечисленных элементов другие также имеют определенную индуктивность и емкость, например в электрических кабелях распределенные по его длине.

Резонанс токов

Резонанс токов наблюдается в цепях, где индуктивность и емкость соединены параллельно.

Явление заключается в протекании токов большой величины между конденсатором и катушкой, при нулевом токе в неразветвленной части цепи. Это объясняется тем, что при достижении резонансной частоты общее сопротивление Z возрастает. Или простым языком звучит так – в точке резонанса достигается максимальное общее значение сопротивления Z, после чего одно из сопротивлений увеличивается, а другое снижается в зависимости от того растет или снижается частота. Это наглядно отображено на графике:

В общем, всё аналогично предыдущему явлению, условия возникновения резонанса токов следующие:

Частота питания аналогична резонансной у контура.
Проводимости у индуктивности и ёмкости по переменному току равны BL=Bc, B=1/X.

Принцип работы последовательного колебательного контура

Генератор частоты и последовательный колебательный контур

Давайте проведем классический эксперимент, который есть в каждом учебнике по электронике. Для этого соберем вот такую схему:

Генератор (Ген)у нас будет выдавать синус.

Для того, чтобы снять осциллограмму силы тока через последовательный колебательный контур, мы подключим в схему шунтовый резистор с малым сопротивлением в 0,5 Ом и с него уже будем снимать напряжение. То есть в данном случае мы шунт используем для наблюдения силы тока в цепи.

А вот и сама схема в реальности:

Слева-направо: шунтовый резистор, катушка индуктивности и конденсатор. Как вы уже поняли, сопротивление R – это суммарное сопротивление потерь катушки и конденсатора, так как нет идеальных радиоэлементов. Оно “прячется” внутри катушки и конденсатора, поэтому в реальной схеме отдельным радиоэлементом мы его не увидим.

Теперь нам осталось подцепить эту схему к генератору частоты и осциллографу, и прогнать по некоторым частотам, снимая осциллограмму с шунта U_ш, а также снимая осциллограмму с самого генератора U_ГЕН.

С шунта мы будем снимать напряжение, которое у нас отображает поведение силы тока в цепи, а с генератора собственно сам сигнал генератора. Давайте прогоним нашу схемку по некоторым частотам и глянем что есть что.

Влияние частоты генератора на сопротивление колебательного контура

В схеме я взял конденсатор на 1мкФ и катушку индуктивности на 1 мГн. На генераторе настраиваю синус размахом в 4 Вольта. Вспоминаем правило: если в цепи соединение радиоэлементов идет последовательно друг за другом, значит, через них течет одинаковая сила тока.

Красная осциллограмма – это напряжение с генератора частоты, а желтая осциллограмма – отображение силы тока через напряжение на шунтовом резисторе.

Частота 200 Герц с копейками:

Как мы видим, при такой частоте ток в этой цепи есть, но очень слабый

Добавляем частоту. 600 Герц с копейками

Здесь мы уже отчетливо видим, что сила тока возросла, а также видим, что осциллограмма силы тока опережает напряжение. Попахивает реактивным сопротивлением конденсатора.

Добавляем частоту. 2 Килогерца

Сила тока стала еще больше.

3 Килогерца

Сила тока увеличилась. Заметьте также, что сдвиг фаз стал уменьшаться.

4,25 Килогерц

Осциллограммы почти уже сливаются в одну. Сдвиг фаз между напряжением и силой тока становится почти незаметным.

И вот на какой-то частоте у нас сила тока стала максимальной, а сдвиг фаз стал равен нулю. Запомните этот момент. Для нас он будет очень важен.

Ну а давайте далее будем увеличивать частоту. Смотрим, что получается в итоге.

Еще совсем недавно ток опережал напряжение, а сейчас уже стал запаздывать после того, как выровнялся с ним по фазе. Так как ток уже отстает от напряжения, здесь уже попахивает реактивным сопротивлением катушки индуктивности.

Увеличиваем частоту еще больше

Сила тока начинает падать, а сдвиг фаз увеличивается.

22 Килогерца

74 Килогерца

Как вы видите, с увеличением частоты, сдвиг приближается к 90 градусов, а сила тока становится все меньше и меньше.

Область применения

Это явление в цепи колебательного контура имеет тенденцию к затуханию. Чтобы стало возможным использовать это явление в различных приборах и устройствах, необходимо постоянно поддерживать характеристики электричества в заданных пределах. Сделать этот процесс постоянным очень просто: достаточно подпитывать систему переменным напряжением с постоянными значениями частоты.

Радиовышка

Важно! Эффект резонанса широко применяется в различных радиопередающих и принимающих сигнал устройствах. Наиболее часто, это явление используется в различных фильтрах

Например, если на пути входящего электрического сигнала необходимо избавиться от составляющей определённой частоты, то параллельно проводнику устанавливают конденсатор, резистор и дроссель. Если фильтр необходим для того, чтобы «пропустить» сигнал определенной частоты, то также изготавливается фильтр из ёмкости, сопротивления и индуктивности, но подключается такая система последовательно

Наиболее часто, это явление используется в различных фильтрах. Например, если на пути входящего электрического сигнала необходимо избавиться от составляющей определённой частоты, то параллельно проводнику устанавливают конденсатор, резистор и дроссель. Если фильтр необходим для того, чтобы «пропустить» сигнал определенной частоты, то также изготавливается фильтр из ёмкости, сопротивления и индуктивности, но подключается такая система последовательно.

Электрический фильтр

Использовать эффект резонанса можно и для повышения напряжения. Например, в ситуации, когда электрический двигатель не способен работать на расчетных показателях мощности по причине низкого напряжения, достаточно установить по мощному конденсатору на каждую фазу, чтобы полностью разрешить проблему.

Резонанс в электрической цепи может возникать при наличии определенных условий, поэтому от него можно избавиться либо вызвать намеренно. Если такое явление является нежелательным, то, во многих случаях, достаточно изменить рабочую частоту или увеличить сопротивление, чтобы полностью устранить это паразитическое явление. Простейшая система этого типа состоит из конденсатора, резистора и дросселя, поэтому, при необходимости, можно легко собрать устройство, в котором это электрический эффект будет выполнять какую-либо полезную функцию.

Источник

Емкость и индуктивность в цепи переменного тока

Если в цепях постоянного тока емкость в общем смысле представляет собой разорванный участок цепи, а индуктивность — проводник, то в переменном конденсаторы и катушки представляют собой реактивный аналог резистора.

Реактивное сопротивление катушки индуктивности определяется по формуле:

Векторная диаграмма:

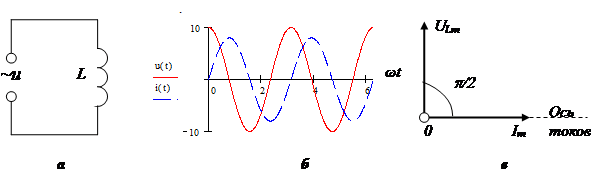
Реактивное сопротивление конденсатора:

Здесь w — угловая частота, f — частота в цепи синусоидального тока, L — индуктивность, C — емкость.

Векторная диаграмма:

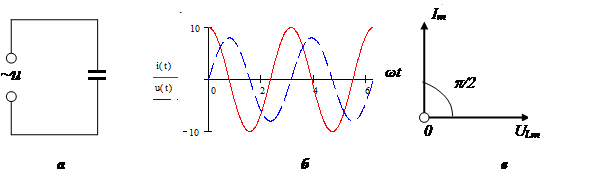
Стоит отметить, что при расчете соединенных последовательно реактивных элементов используют формулу:

Обратите внимание, что емкостная составляющая принимается со знаком минус. Если в цепи присутствует еще и активная составляющая (резистор), то складывают по формуле теоремы Пифагора (исходя из векторной диаграммы):. От чего зависит реактивное сопротивление? Реактивные характеристики зависят от величины емкости или индуктивности, а также от частоты переменного тока

От чего зависит реактивное сопротивление? Реактивные характеристики зависят от величины емкости или индуктивности, а также от частоты переменного тока.

Если посмотреть на формулу реактивной составляющей, то можно заметить, что при определенных значениях емкостной или индуктивной составляющей их разность будет равна нулю, тогда в цепи останется только активное сопротивление. Но это не все особенности такой ситуации.

Последовательное соединение

Катушка индуктивности и последовательно включенный в цепь конденсатор вместе особенным образом воздействуют на генератор, от которого запитана цепь. Также они влияют на фазовые соотношения напряжения и тока:

Первый элемент сдвигает фазу, при этом напряжение начинает обгонять ток примерно на четверть периода.
Второй элемент действует иначе. Он заставляет ток обгонять напряжение также на одну четвертую часть периода фазы.

Индуктивное сопротивление действует на смещение фаз, из-за чего его можно считать противоположным работе емкостного сопротивления. В результате итоговый сдвиг фаз между напряжением и током в цепи зависит от суммарного действия индуктивного и емкостного сопротивлений, а также соотношения между ними. От этого тоже зависит характер цепи.

Общее реактивное сопротивление определить просто. Необходимо сложить два показателя сопротивления:

Индуктивное от катушки.
Емкостное от конденсатора.

Из-за того, что они оказывают противоположное воздействие, одному из них присваивается отрицательный знак (обычно ёмкостному сопротивлению конденсатора). Тогда общее реактивное сопротивление можно найти так: из показателя катушки вычесть конденсатор. Если общее напряжение разделить на найденный параметр, то по закону Ома получится сила тока. Эту формулу можно легко изменить, переведя на напряжение. Оно будет равно произведению силы тока и разности двух сопротивлений (индуктивное берется с катушки, а емкостное — с конденсатора).

Если раскрыть скобку, то первое значение отразит действительный показатель части общего напряжения, которая старается преодолеть сопротивление. Второе — слагающая всего напряжения, которая пытается преодолеть емкостный параметр. Так, общее напряжение можно рассматривать как сумму этих слагаемых.

https://youtube.com/watch?v=KB0eMQ8loy0

Для определения этого значения нужно вычислить квадратный корень из суммы двух частей:

Общее активное сопротивление, возведенное в квадрат.
Квадрат разности индуктивного и емкостного сопротивлений, то есть общее реактивное.

https://youtube.com/watch?v=vp-uTZ_0FrQ

Резонанс в электрической цепи

Определение 2

Резонанс в электрической цепи – это резкое возрастание амплитуды внутренних колебаний системы за счет совпадения частоты внутренних колебаний с частотой внешнего воздействия.

Схема \(RLC\) – это электрическая цепь с последовательными, параллельными или комбинированными соединениями компонентов (резисторами, индукционными катушками и конденсаторами). \(RLC\) – это сочетание сопротивления, индуктивности и емкости.

Векторная диаграмма в случае последовательного соединения \(RLC\)-цепи бывает емкостной, активной или индуктивной.

В индуктивной векторной диаграмме резонанс напряжений появляется лишь при нулевом сдвиге фаз и совпадении сопротивлений индукции и емкости.

Сложно разобраться самому?

Попробуй обратиться за помощью к преподавателям

Решение задач Контрольные работы Эссе

Электроника

В электрических цепях резонансом называется такой режим пассивной цепи, содержащий катушки индуктивности и конденсаторы, при котором ее входное реактивное сопротивление или ее входная реактивная проводимость равны нулю. При резонансе ток на входе цепи, если он отличен от нуля, совпадает по фазе с напряжением.

В электрических цепях резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.

Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником.

Электрическое устройство, состоящее из ёмкости и индуктивности, называется колебательным контуром. Элементы колебательного контура могут быть включены как последовательно (тогда возникает резонанс напряжений), так и параллельно (резонанс токов). При достижении резонанса, импеданс последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален. Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. В то же время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов.

Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения

ωL=1ωC⇒ω=1LC{\displaystyle \omega L={\frac {1}{\omega C}}\Rightarrow \omega ={\frac {1}{\sqrt {LC}}}},

где ω=2πf{\displaystyle \omega =2\pi f} ; f — резонансная частота в герцах; L — индуктивность в генри; C — ёмкость в фарадах

Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется добротностью системы.. В электронных устройствах также применяются различные электромеханические резонансные системы.

В электронных устройствах также применяются различные электромеханические резонансные системы.

Подробнее по этой теме см. Кварцевый резонатор.
Подробнее по этой теме см. Электромеханический фильтр.

Для чего используется резонанс

Как явление, резонанс напряжений часто используется в различных фильтрах электрического типа. Например, если есть необходимость устранения из сигнала передачи некоторой составляющей тока определенной частоты, то к приемнику параллельно подключают катушку и конденсатор, которые по отношению друг к другу соединены последовательно. В результате подобных действий электроток определенной резонансной частоты замкнется через цепочку дроссель-конденсатор и не попадет на приемник.

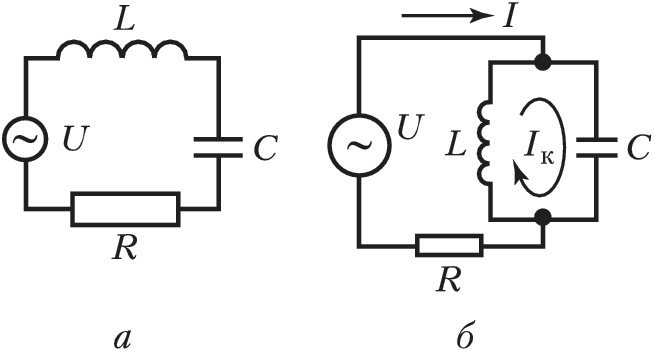
Колебательный контур

Важно! Сам по себе резонанс напряженности в электричестве — явление негативное, так как он способствует появлению перенапряжений на некоторых участках соединения и выводит из строя приборы

Примеры применения на практике

Классическим примером применения резонанса колебательных контуров является настройка радиоприёмника на частоту соответствующей радиостанции. В качестве рабочего элемента настроечного узла используется конденсатор с регулируемой ёмкостью. Вращение ручки настройки изменяет ёмкость конденсатора, а значит и резонансную частоту контура.

В момент совпадения резонансной частоты с рабочей частотой какой-либо радиостанции возникает резонанс напряжений, в результате которого резко возрастает амплитуда колебаний принятой радиоприёмником частоты. Специальные фильтры отделяют эти колебания от несущих радиочастот, а усилители усиливают полученные сигналы. В динамике появляются звуки, генерируемые передатчиком радиостанции.

Колебательные контуры, построенные на принципе последовательного соединения LC-элементов, применяются в цепях питания высокоомных нагрузок, потребляющих токи повышенного напряжения. Такие же устройства применяют в полосовых фильтрах.

Последовательный резонанс применяют при пониженных напряжениях сети. В этом случае используют реактивную энергию обмоток трансформатора, соединённых последовательно.

Конденсаторы и различные катушки индуктивности (рис. 5) входят в конструкцию практически всех аналоговых устройств. Они используются для настройки фильтров или для управления токами в отдельных узлах.

Катушки индуктивности

Важно знать, что резонансные контуры не увеличивают количество электрической энергии в цепях. Они лишь могут повышать напряжения, иногда до опасных значений

Постоянный ток не причиной резонансных явлений.